不同偏心度的環空渦動流場特性

張晉凱李根生黃中偉田守嶒宋先知王海柱. 油氣資源與探測國家重點實驗室；2. 中國石化石油工程技術研究院

不同偏心度的環空渦動流場特性

張晉凱1，2李根生1黃中偉1田守嶒1宋先知1王海柱1
1. 油氣資源與探測國家重點實驗室；2. 中國石化石油工程技術研究院

為了深入研究環空渦動時的流場特性，根據流體力學理論，以連續性方程和N-S方程為控制方程，利用計算流體力學技術對鉆柱渦動時環空赫巴流體的流動進行了系統的數值模擬，研究了不同公轉方向下鉆柱偏心度的變化對環空切向速度剖面與合速度剖面的影響。通過對模擬數據的對比分析，發現不同公轉方向下環空流場分布截然不同，正向公轉時切向速度在環空寬間隙處隨著公轉速度、自轉速度和偏心度增大正向增大；反向公轉時會出現二次流，切向速度在環空寬間隙處隨偏心度的減小整體反向減小，同時二次流趨勢越明顯，摩阻壓耗越大。合理應用這些規律有助于完善現有鉆井水力學理論，更好地揭示井下環空流場特性，并為鉆井水力參數優化設計提供有效的理論指導。

渦動；環空；赫巴流體；摩阻壓耗；數值模擬；流場

鉆進過程中鉆柱在井筒內一般會出現渦動，即在地面轉盤帶動下順時針自轉的同時還繞井眼軸線公轉。渦動的出現以及公轉的半徑（即渦動時鉆柱的偏心度）和方向（順時針方向、逆時針方向）就目前鉆井水平而言無法控制且很難預測，通過實驗難以揭示其內部規律，最可行的方法是借助數值模擬技術進行研究［1-5］。因此研究渦動時的偏心度對由自轉旋流場、公轉旋流場和軸向流場疊加而成的環空真實流場［6-12］的影響有助于完善現有鉆井水力學理論，更好地揭示井下環空流場特性，并為鉆井水力參數優化設計提供理論指導［13-16］。

1 環空流動的建模與模擬Model building and simulation of flows in annulus

1.1鉆井液模型

Model for drilling fluids

為更好地描述非牛頓不可壓縮流體的流變特性，采用了更為合理的赫巴流變模式，該模式也可看作修正的冪律模式，具體方程為［17］

式中，τ為剪切應力，Pa；τHB為該模式的屈服值，Pa；K為稠度系數，Pa·sn；n為流性指數，無因次；γ為剪切速率，s-1。屈服值是鉆井液的實際動切力。根據文獻［18-19］內的具體數據，采用其中的一種油基鉆井液的數據，回歸出相應的赫巴模式的具體參數

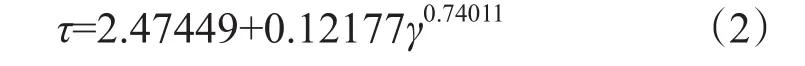
1.2幾何模型

Geometric model

數值模擬所涉及到的幾何尺寸均采用現場實際尺寸，鉆柱外徑139.7 mm，套管內徑244.0 mm，環空長度15 m，其他參數見表1。選取15 m長的環空鉆井液作為研究對象，采用基于交錯網格的SIMPLEC算法對連續性方程和N-S方程進行離散化，動量方程的對流項進行離散化時為保證計算精度，采用二階格式；建立的網格幾何模型如圖1。

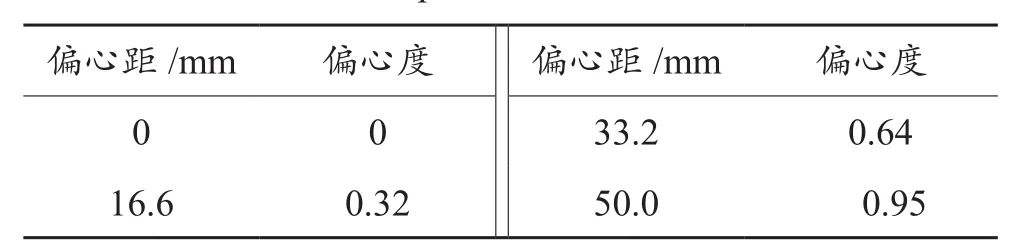
表1　環空流動幾何參數Table 1 Geometric parameters for flows in annulus

設置3類邊界類型：速度入口邊界，壓力出口邊界以及旋轉壁面邊界，設定該邊界繞其自身軸線自轉的同時繞井壁軸線公轉，井壁為靜止壁面，所有壁面都簡化為無滑移水力光滑的壁面，且近壁面處的網格加密劃分，采用柱坐標系，對稱軸為z軸，按照速度分量方式設定速度入口值［20］。

圖1　不同偏心度下環空流體區域的幾何網格模型Fig.1 Geometric grid model for flowing zones in annulus with various eccentricities

1.3流動模型

Flow model

將流體視為不可壓縮流體，且具有一定的黏度值和密度值，不考慮傳熱和重力的影響［21］。用連續性方程和N-S方程共同描述環空流動，基于有限體積法的思想進行離散。由于渦動時的環空流場屬于復雜的旋流場，流體質點脈動程度較高，因此采用湍流兩方程模型中的Realizable模型，該模型能夠有效地將湍動黏度模型中的系數與應變率耦合起來，能夠更為精確地描述包括旋轉均勻剪切流、包含有射流和混合流的自由流、管道內流動、邊界層流動以及帶有分離的流動。因此文中采用Realizable模型［22］。

1.4環空流動的數值模擬

Numerical simulation for flows in annulus

渦動時自轉和公轉坐標系都遵循右手準則，規定轉盤自轉為順時針方向，以此作為旋轉正方向，鉆柱在井眼內的公轉根據已有研究的描述有順時針和逆時針2個方向，當公轉為順時針時，與自轉方向一致，根據右手準則，為正向渦動，反之為反向渦動。

為更好地研究不同偏心度下流場的變化規律，設置其余鉆井參數在合理范圍，如表2。

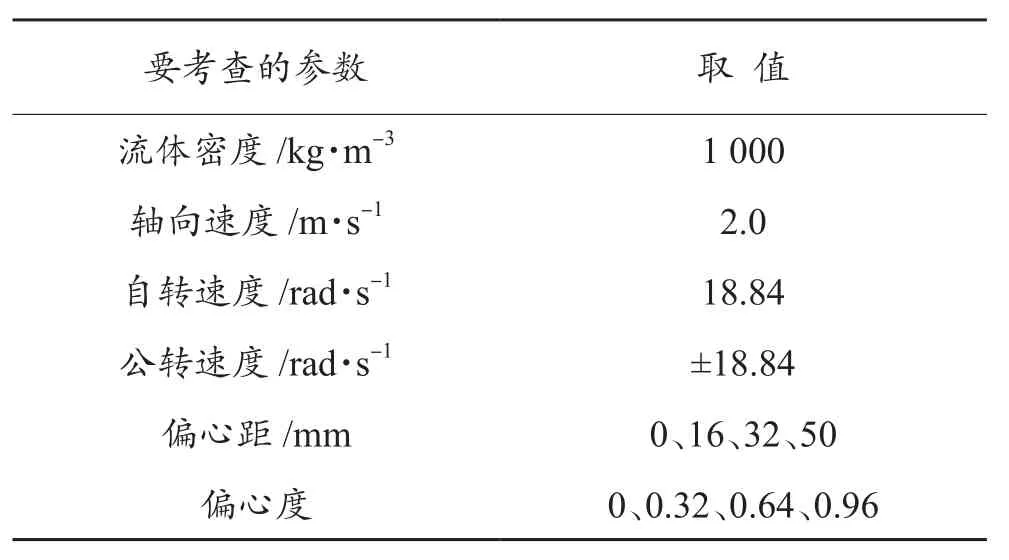
表2　鉆柱渦動時環空流動數值模擬參數設置Table 2 Parameters for numerical simulation of flows in annulus during drill pipe vortex

取15 m長偏心環空鉆井液距入口9 m處橫截面上沿對稱軸的剖面進行分析，橫坐標0表示井筒中軸線。

2 鉆柱渦動時環空流場特性分析Features of flow field in annulus during drill pipe vortex

設井筒圓心為O1，鉆柱圓心為O2，井筒半徑為R，鉆柱半徑為r，偏心距為h，公轉速度為ω1，自轉速度為ω2，P1為最寬間隙處對應的鉆柱外壁面位置，P2為最窄間隙處對應的鉆柱外壁面位置。設圖2中時刻的自轉線速度方向為正方向，根據分析可知：

當自轉與公轉同向，P1點和P2點的線速度（切向速度）分別為

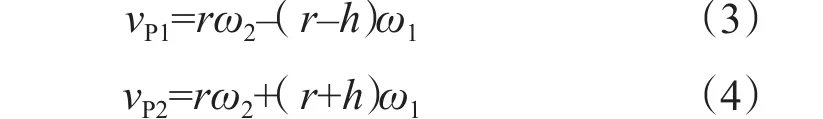
當自轉與公轉反向，P1點和P2點的線速度（切向速度）分別為

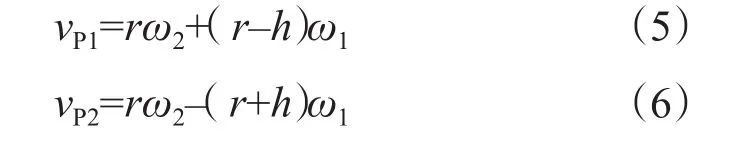
2.1偏心度對流速剖面的影響

Impacts of eccentricity on flow velocity profile

分析模擬數據發現，其他條件不變時，隨軸向流速增大，環空內寬窄間隙處合速度剖面變化規律與一般環空流動相同，由于徑向速度較小且變化不明顯，本研究未作討論。下面著重分析渦動時的偏心度及公轉正反方向的變化對環空氣場的影響。

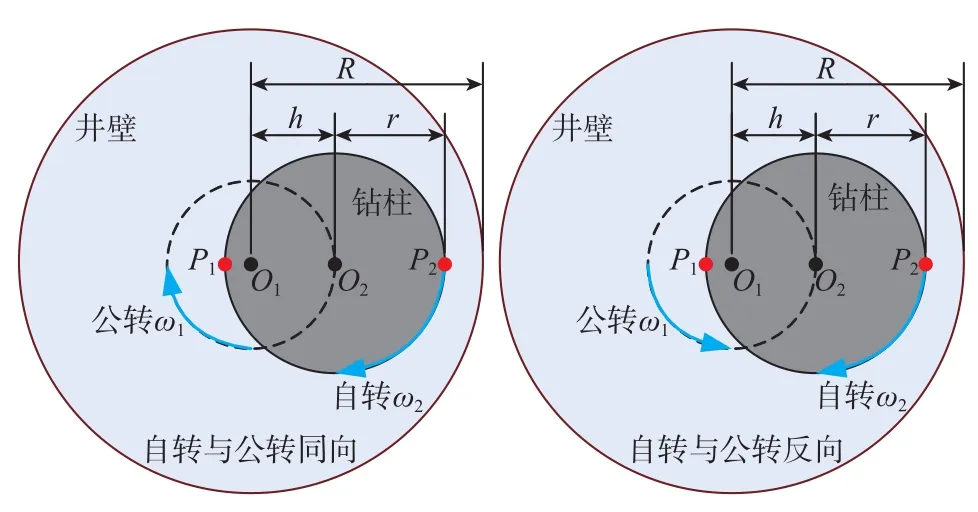
圖2　鉆柱渦動原理圖Fig.2 Principles of drill pipe vortex

設定環空鉆井液密度為1.0 g/cm3，軸向流速為2.0 m/s，公轉速度為18.84 rad/s，自轉速度為18.84 rad/s，考查偏心度分別為0.32、0.64、0.95時各流動參數剖面的變化規律。

切向速度剖面：偏心度增大，寬間隙處切向速度剖面變大變寬，窄間隙處的切向速度剖面整體增大，鉆柱外壁面在寬間隙處根據式（3）的推導切向速度越小，在窄間隙處根據式（4）的推導切向速度越大，如圖3a。合速度剖面：偏心度增大，寬間隙處合速度剖面整體增大，窄間隙處合速度剖面整體減小，鉆柱外壁面在寬窄間隙處的變化規律同切向速度的變化規律，如圖3b。

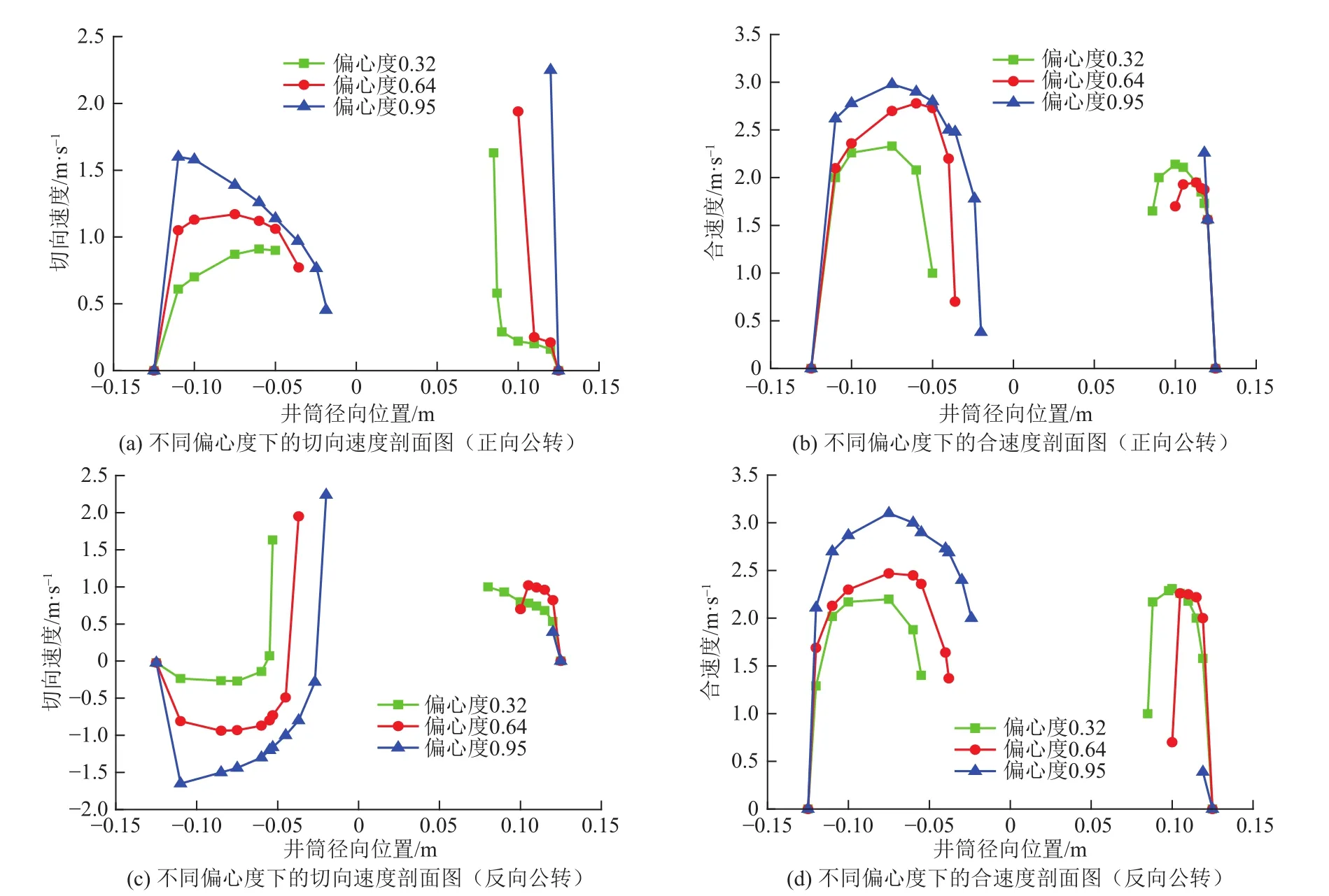
圖3　偏心度對流場速度剖面的影響Fig.3 Impacts of eccentricity on flow field velocity profile

設定環空鉆井液密度為1 000 kg/m3，軸向流速為2.0 m/s，公轉速度為-18.84 rad/s，自轉速度為18.84 rad/s，考查偏心度分別為0.32、0.64、0.95時各流動參數剖面的變化規律。

切向速度剖面：隨偏心度增大，寬間隙處的切向速度剖面整體反向增大，窄間隙處的切向速度剖面先增大后減小，鉆柱外壁面在寬間隙處根據式（5）的推導切向速度正向增大，在窄間隙處根據式（6）的推導切向速度減小，井壁處切向速度為0，如圖3c。

合速度剖面：隨偏心度增大，寬間隙處合速度剖面整體增大，窄間隙處的合速度剖面整體減小，鉆柱外壁面寬窄間隙處的變化規律同切向速度的變化規律，如圖3d。

2.2二次流的分析

Analysis for secondary flows

反向公轉時，寬間隙鉆柱外壁面附近的流體質點跟隨鉆柱自轉呈正向旋轉，此處的切向速度為正值，但在遠離鉆柱外壁面的區域，由于鉆柱正向自轉的趨勢弱于反向公轉的趨勢，故此區域的流體質點跟隨鉆柱反向公轉，所以此處切向速度為負值，如圖3c所示。在寬間隙區域，同時出現正反2個方向的切向速度，兩股不同方向的旋流在環空窄間隙的兩側分離與匯合，使得環空寬間隙處出現一個明顯的大渦，環空窄間隙處由于鉆柱旋轉壁面帶動的旋流將本應對應出現的另一個不對稱的小渦淹沒，最終形成了不對稱的二次流，如圖4所示。

圖4　不同偏心度下的截面二次流矢量圖（ρ=1 000 kg/m3，v=2.0 m/s，ω1=-18.84 rad/s，ω2=18.84 rad/s）Fig.4 Vector diagram for secondary flows under different eccentricities（ρ=1 000 kg/m3，v=2.0 m/s，ω1=-18.84 rad/s，ω2=18.84 rad/s）

反向公轉時，其他參數不變，偏心度越大，越不容易出現二次流。寬間隙處二次流產生的大渦越靠近旋轉鉆柱外壁面，同時二次流的分離與匯合點越靠近窄間隙處，當偏心度大到一定程度后，鉆柱的正向自轉趨勢被二次流在寬窄間隙處的反向流動趨勢完全包裹且基本抵消掉，此時狀態與偏心環空自轉的螺旋流場（自轉方向為反向，自轉速度大小同公轉）最為接近。二次流的明顯出現使得環空流體質點的脈動趨勢進一步加強，隨著偏心度減小，鉆柱正向自轉趨勢越不容易被抵消，二次流趨勢越明顯，偏心環空流動的摩阻壓耗將進一步增大。

3 結論Conclusions

（1）偏心度對渦動流場的影響較為復雜，不能輕易忽略。宏觀上不論公轉方向如何，隨偏心度增大，寬間隙處的合速度剖面整體增大，窄間隙處的合速度剖面整體減小，但當具體分析不同公轉方向的環空流場時，又有各自截然不同的流動特性。

（2）正向公轉時，鉆柱的自轉和公轉共同增強了寬窄間隙處的正向旋流趨勢，此時切向速度整體為正值，無二次流出現，偏心度增大，寬間隙處切向速度增大。

（3）反向公轉時，切向速度同時出現正反向旋流趨勢，鉆柱的公轉流場與自轉流場出現相互抵消狀態，環空截面呈現不對稱的二次流。偏心度減小，寬間隙處切向速度反向越小，公轉流場與自轉流場相互抵消越小，二次流趨勢越明顯，摩阻壓耗越大。

References：

［1］魏淑惠. 基于計算流體動力學的偏心環空流場數值模擬［J］.大慶石油學院學報，2007，31（6）：62-64.

WEI Shuhui. CFD numerical simulation of eccentric annuli flow field.［D］. Daqing： Dqing Petroleum Institute， 2007， 31（6）： 62-64.

［2］王常斌，陳皖，田迪，賈雪松，趙海燕.冪律流體偏心環空流場CFD模擬［J］. 鉆井液與完井液，2009，26（3）：62-64.

WANG Changbin， CHEN Wan， TIAN Di， JIA Xuesong，ZHAO Haiyan. A CFD simulation of the flow field of a power law fluid in an eccentric annulus［J］. Drilling Fluid & Completion Fluid， 2009， 26（3）： 62-64.

［3］陳皖. 偏心環空流場的數值模擬［D］. 大慶： 大慶石油學院，2009：62-64.

CHEN Wan. Numerical simulation of flow field in eccentric annulus［D］. Daqing： Dqing Petroleum Institute， 2009： 62-64.

［4］朱云偉. 赫巴流體環空流動的CFD模擬［D］. 大慶：東北石油大學，2011：50-52.

ZHU Yunwei. CFD simulation of Herschel-Bulkley fluid flow in annulus［D］. Daqing： Northeast Petroleum University， 2011： 50-52.

［5］李子豐，梁爾國.鉆柱力學研究現狀及進展［J］.石油鉆采工藝，2008，30（2）：1-9.

LI Zifeng， LIANG Erguo. Research and development of drill string mechanics［J］. Oil Drilling & Production Technology， 2008， 30（2）： 1-9.

［6］陳庭根，管志川，劉希圣.鉆井工程理論與技術［M］.東營：石油大學出版社，2000.

CHEN Tinggen， GUAN Zhichuan， LIU Xisheng. Drilling engineering theory and technology［M］. Dongying：University of Petroleum Press， 2000.

［7］高德利.鉆井科技發展的歷史回顧現狀分析與建議［J］.石油科技論壇，2004，23（2）：29-39.

GAO Deli. Analysis and suggestion on the history of the development of drilling technology［J］. Petroleum Science and Technology Forum， 2004， 23（2）： 29-39.

［8］高德利.油氣井管柱力學與工程［M］.東營：中國石油大學出版社，2006.

GAO Deli. Down-hole tubular mechanics and its applications［M］. Dongying： University of Petroleum Press， 2006.

［9］章揚烈.鉆柱運動學與動力學［M］.北京：石油工業出版社，2001.

ZHANG Yanglie. Drillstring kinematics and dynamics ［M］. Beijing： Petroleum Industry Press， 2001.

［10］狄勤豐，王文昌，胡以寶，張小柯.鉆柱動力學研究及應用進展［J］.天然氣工業，2006，26（4）：57-59.

DI Qinfeng， WANG Wenchang， HU Yibao， ZHANG Xiaoke. Study and application of Drilling string dynamics［J］. Natural Gas Industry， 2006， 26（4）： 57-59.

［11］《中國石油鉆井》編輯委員會.中國石油鉆井（綜合卷）［M］.北京：石油工業出版社，2007.

CHINA PETROLEUM DRILLING editorial board. China petroleum drilling（comprehensive volume） ［M］. Beijing： Petroleum Industry Press， 2007.

［12］李子豐，王兆運，陽鑫軍，田新民.鉆柱渦動分析及防渦穩定器設計［J］. 石油鉆采工藝，2008，30（3）：124-127.

LI Zifeng， WANG Zhaoyun， YANG Xinjun， TIAN Xinmin. Swirling analysis of drilling strings and antiwhirl stabilizers design［J］. Oil Drilling & Production Technology， 2008， 30（3）： 124-127.

［13］REHM B， SCHUBERT J， HAGHSHENAS A，PAKNEJAD A S. Managed pressure drilling［M］. Houston： Gulf Publishing Company， 2008.

［14］KOK M V. TERCAN E. Managed pressure drilling techniques， equipments， and applications［J］. Energy Sources Part A-Recovery Utilization and Environmental Effects. 2012， 34： 591.

［15］GODHAVN J M. Control requirements for automatic managed pressure drilling system［J］.SPE Drilling & Completion. 2010，25（3）： 336-338.

［16］ZHOU J， STAMNES O N， AAMO O M， KAASA G O. Switched control for pressure regulation and kick attenuation in a managed pressure drilling system［J］. IEEE Transactions on Control Systems Technology. 2011，19（2）： 337-379.

［17］HERSCHEL W H， BULKLEY R. Measurement of consistency as applied to rubber-benzene solutions：29th Annual Meeting of the American Society Testing Materials Atlantic City， June 1926 ［C］. Proc. ASTM，26 （II） ： 621-633.

［18］胡茂炎，尹文斌，鄭秀華，夏柏如.鉆井液流變參數計算方法的分析及流變模式的優選［J］.探礦工程：巖土鉆掘工程，2004，（7）：41-45.

HU Maoyan， YIN Wenbin， ZHENG Xiuhua， XIA Boru. Analyses on calculation methods of rheological parameters of drilling fluid and optimization of rheological model［J］. Exploration Engineering：Drilling & Tunneling，2004，（7）： 41-45.

［19］韓洪升，魏兆勝，崔海青，李昌連.石油工程非牛頓流體力學［M］.哈爾濱：哈爾濱工業大學出版社，1993：116-145.

HAN Hongsheng， WEI Zhaosheng， CUI Haiqing， LI Changlian. Non-newtonian fluid mechanics in petroleum engineering［M］. Haerbin： Harbin Institute of Technology Press， 1993： 116-145.

［20］張晉凱，李根生，黃中偉，田守嶒，宋先知.連續油管螺旋段摩阻壓耗數值模擬［J］.中國石油大學學報：自然科學版2012，36（2）：115-119.

ZHANG Jinkai， LI Gensheng， HUANG Zhongwei，TIAN Shouceng， SONG Xianzhi. Numerical simulation on friction pressure loss in helical coiled tubing［J］. Journal of China University of Petroleum： Edition of Natural Science， 2012， 36（2）： 115-119.

［21］高學平.高等流體力學［M］.天津：天津大學出版社，2005：16-28.

GAO Xueping. Advanced fluid mechanics［M］. Tianjin： Tianjin University Press， 2005： 16-28.

［22］王福軍.計算流體動力學分析——CFD 軟件原理與應用［M］.北京：清華大學出版社，2004：122-126.

WANG Fujun. Computational fluid dynamics analysis-Software principles and applications of CFD［M］. Beijing： Tsinghua University Press， 2004： 122-126.

（修改稿收到日期 2016-01-28）

〔編輯 薛改珍〕

Features of vortex flow fields in annuluses with different eccentricities

ZHANG Jinkai1，2， LI Gensheng1， HUANG Zhongwei1， TIAN Shouceng1， SONG Xianzhi1， WANG Haizhu1
1. State Key Laboratory of Petroleum Resources and Prospecting， Beijing 102249， China；2. SINOPEC Research Institute of Petroleum Engineering， Beijing 100101， China

To further understand features of flow field during vortex in annulus， impacts of eccentricity variations on tangential velocity profile and resultant velocity profile of annulus under different rotation directions were determined according to the fluid dynamics theories and with continuity equation and N-S equation as controlling equations. In this study， systematic numerical simulations were performed on flows of Hershel-Bulkley fluid in annulus during vortex of drill pipes by using fluid dynamics. Through comparison of simulation data， it is seen that distributions of flow fields in the annulus are significantly different in different rotation directions. During rotation in positive direction， tangential velocity increases with the increases of revolution speed， speed of autorotation and eccentricity around wide clearance of annulus. During rotation in negative position， secondary flows are observed， and tangential velocity decreases reversely with the decreases of eccentricity in wide clearance of the annulus. Moreover， more obvious the trends of secondary flows， higher the frictional pressure losses. Proper application of these patterns may improve existing hydraulic theories for drilling operations to highlight properties of flow fields in the annulus and to provide theoretical guidance for design and optimization of hydraulic parameters for drilling operations.

vortex； annulus； Hershel-Bulkley fluid； frictional pressure loss； numerical simulation； flow field

ZHANG Jinkai， LI Gensheng， HUANG Zhongwei， TIAN Shouceng， SONG Xianzhi， WANG Haizhu. Features of vortex flow fields in annuluses with different eccentricities［J］.Oil Drilling & Production Technology， 2016， 38（2）： 133-137.

TE21

A

1000 -7393（ 2016 ） 02 -0133-05

10.13639/j.odpt.2016.02.001

國家重點基礎研究發展計劃（973計劃）“深井復雜地層安全高效鉆井基礎研究”（編號：2010CB226704）。

張晉凱（1980-），2013年畢業于中國石油大學（北京）油氣井工程專業，現從事油氣井流體力學與工程方面的研究。通訊地址：（100101）北京市朝陽區北辰東路8號北辰時代大廈10層。E-mail：bob33@163.com

李根生（1961-），中國工程院院士，教授，博士生導師，從事油氣鉆井和完井工程方面的研究和教學。通訊地址：（102249）北京市昌平區府學路18號中國石油大學（北京）石油工程學院。電話：010-89733935。E-mail：ligs@cup.edu.cn

引用格式：張晉凱，李根生，黃中偉，田守嶒，宋先知，王海柱.不同偏心度的環空渦動流場特性［J］.石油鉆采工藝，2016，38（2）：133-137.