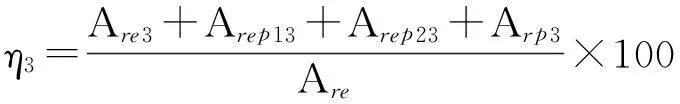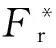尺度相關(guān)的分形粗糙表面彈塑性接觸力學(xué)模型

成雨, 原園, 甘立, 徐穎強, 李萬鐘

(1.西安理工大學(xué) 機械與精密儀器工程學(xué)院, 陜西 西安　710048;2.西北工業(yè)大學(xué) 機電學(xué)院, 陜西 西安　710072)

?

尺度相關(guān)的分形粗糙表面彈塑性接觸力學(xué)模型

成雨1, 原園1, 甘立1, 徐穎強2, 李萬鐘2

(1.西安理工大學(xué) 機械與精密儀器工程學(xué)院, 陜西 西安710048;2.西北工業(yè)大學(xué) 機電學(xué)院, 陜西 西安710072)

摘要：依據(jù)分形理論,研究了粗糙表面間的真實接觸狀況,建立了粗糙表面間的分形接觸模型。考慮微凸體的等級,確定了彈性臨界等級、第一彈塑性臨界等級和第二彈塑性臨界等級的表達(dá)式,研究了粗糙表面中單個微凸體的彈性、彈塑性及完全塑性變形的存在條件,推導(dǎo)出各個等級微凸體的臨界接觸面積的解析式。在此基礎(chǔ)上應(yīng)用微凸體的面積分布密度函數(shù),獲得了接觸表面上接觸載荷與真實接觸面積之間的關(guān)系。計算結(jié)果表明:單個微凸體的臨界接觸面積是和微凸體的尺度相關(guān),隨著微凸體等級的增大而減小;微凸體的變形順序為彈性變形、彈塑性變形和完全塑性變形,與傳統(tǒng)的接觸模型一致;在整個粗糙表面接觸過程中,粗糙表面變形過程與單個微凸體的變形過程一致;最大微凸體所處的等級范圍不同,粗糙表面所表現(xiàn)的力學(xué)性能也不相同。

關(guān)鍵詞：粗糙表面;微凸體;尺度;臨界接觸面積;彈塑性接觸

粗糙表面間接觸特性的研究對分析其摩擦、磨損、導(dǎo)電、導(dǎo)熱等性能具有重要影響。早期的研究主要是基于統(tǒng)計學(xué)分析的接觸模型,采用的統(tǒng)計參數(shù)與采樣長度和儀器分辨率相關(guān),進而導(dǎo)致對確定粗糙表面的表征和分析結(jié)果不具有唯一性[1-2]。分形幾何理論提出后,迅速應(yīng)用到粗糙表面的接觸問題,利用分形理論建立的粗糙表面接觸模型可以提供多尺度的接觸行為預(yù)測分析。Majumdar等[3]提出以分形幾何為基礎(chǔ)的分形接觸模型(MB模型),但該模型中未考慮微凸體的彈塑性變形,認(rèn)為微凸體的臨界彈性接觸面積與尺度無關(guān),得到接觸過程中微凸體先發(fā)生塑性變形,后發(fā)生彈性變形,這一結(jié)果與傳統(tǒng)的接觸力學(xué)結(jié)果相反;Kogut等[4]用有限元法分析了粗糙表面上單個球狀微凸體與剛性平面的接觸情況(KE模型);Morag等[5]基于分形模型,應(yīng)用Hertz理論證明了微凸體的臨界接觸面積與微凸體的尺寸相關(guān),推導(dǎo)出了接觸變形過程中微凸體先發(fā)生彈性變形,再發(fā)生非彈性變形;然而上述2種模型都只研究了粗糙表面上單個微凸體的變形機制,并沒有考慮整個粗糙表面上的接觸載荷與真實接觸面積之間的關(guān)系。Liou等[6]研究了柱狀粗糙表面與剛性光滑平面的接觸,同樣得到了隨著變形量的不斷增加,微凸體先發(fā)生彈性變形,再發(fā)生彈塑性變形或是完全塑性變形;繆小梅和丁雪興等[7-8]依據(jù)分形理論也推導(dǎo)出了單個微凸體的彈性臨界接觸面積與微凸體的尺度相關(guān)。基于上述研究現(xiàn)狀,依據(jù)分形理論,考慮微凸體的等級,確定了彈性臨界等級、第一彈塑性臨界等級和第二彈塑性臨界等級的表達(dá)式,研究單個微凸體的力學(xué)特性,確定了不同等級微凸體的彈性臨界接觸面積、第一彈塑性臨界接觸面積和第二彈塑性臨界接觸面積。結(jié)合海洋島嶼面積分布規(guī)律建立了粗糙表面彈塑性接觸力學(xué)模型,獲得了不同等級微凸體下整個粗糙表面上接觸總載荷與真實接觸面積之間的關(guān)系。

1粗糙表面幾何模型的建立

粗糙表面具有自仿射與多尺度的分形特性,Majumdar等[3]用Weierstrass-Mandelbrot函數(shù)(W-M函數(shù))來表征粗糙表面二維輪廓曲線,表達(dá)式如下

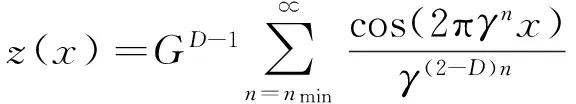
(1)

式中,z(x)表示粗糙表面輪廓曲線的高度;x為輪廓的位移坐標(biāo);D為表面輪廓分形維數(shù);G為輪廓特征尺度系數(shù);γ為大于1的常數(shù),對于服從正態(tài)分布的表面,取γ=1.5[3,5];γn表示輪廓曲線的空間頻率,nmin為與輪廓結(jié)構(gòu)最低截止頻率對應(yīng)的序數(shù)。

輪廓曲線由D、G和nmin3個參數(shù)決定,由于表面輪廓為非平穩(wěn)的隨機過程,最低截止頻率跟取樣長度有關(guān),D和G可由二維W-M函數(shù)的功率譜獲得。

2兩粗糙表面接觸

兩粗糙表面間的接觸可以等效為一個粗糙表面與一個剛性光滑平面的接觸,且等效粗糙表面滿足各向同性的分形特性;忽略接觸過程中微凸體之間的相互作用;假設(shè)變形時只有微凸體發(fā)生變形且不考慮接觸過程中接觸硬化和硬度隨深度的變化;不考慮摩擦。

2.1單個微凸體力學(xué)模型的建立

粗糙表面是由一系列不同尺寸的余弦波狀微凸體疊加而成的,對于任何一個微凸體l=1/γn,變形前的輪廓曲線可定義為

(2)

圖1為單個接觸微凸體變形示意圖,其中l(wèi)為微凸體基底的尺寸,δ為微凸體的幅值,ω為實際變形量,取值范圍為0≤ω≤δ,具體大小與所受載荷有關(guān),l′為用一剛性平面截微凸體所得的截斷長度,lr為微凸體變形量為ω時的實際接觸長度。

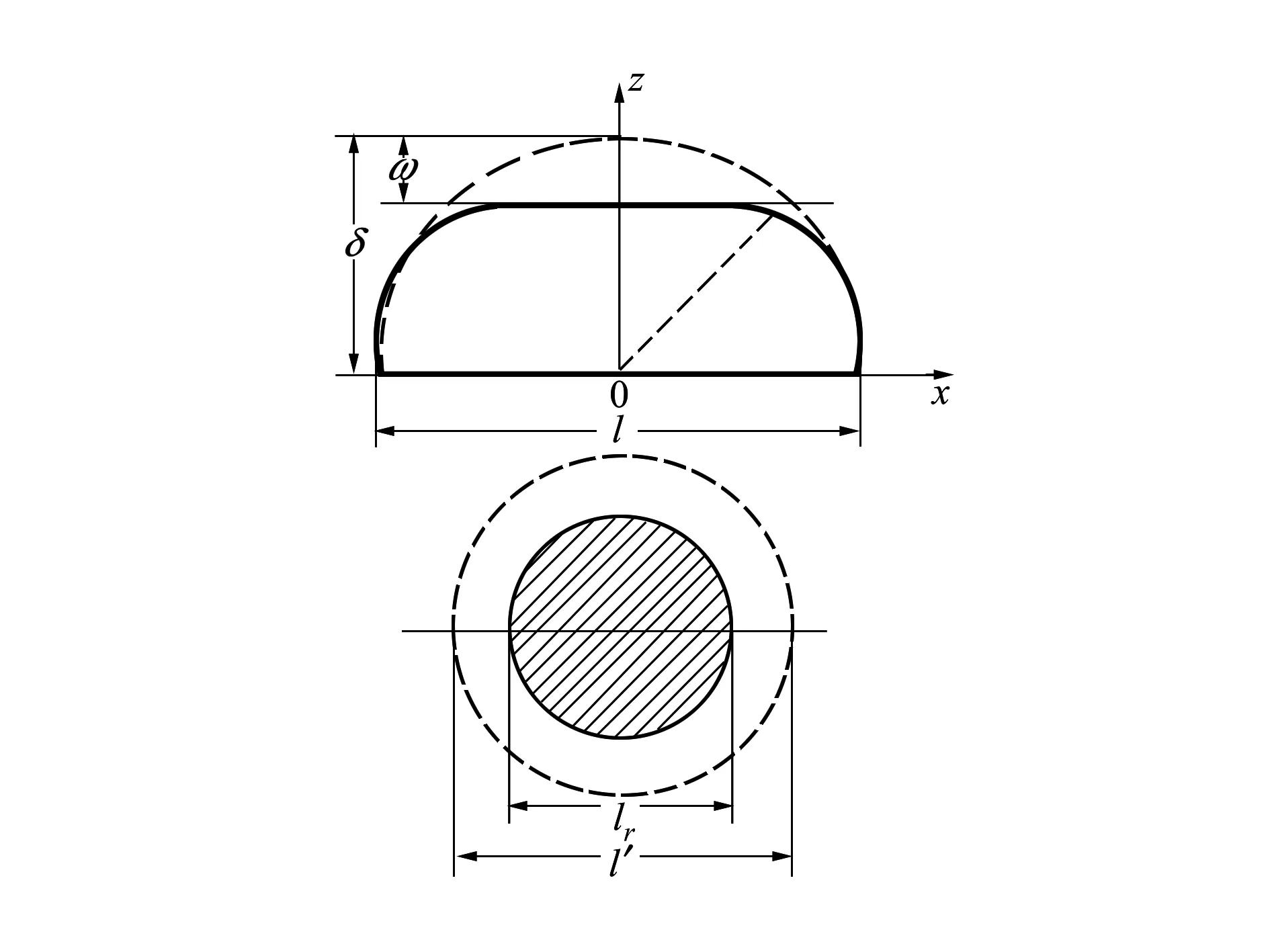
圖1　接觸微凸體變形示意圖

由(2)式可得微凸體頂端曲率半徑R為

(3)

由(2)式可得微凸體的幅值δ為

(4)

當(dāng)截斷長度為l′時,微凸體的實際變形量ω為

(5)

2.2微凸體的變形機制

兩粗糙表面接觸過程中,隨著變形量的不斷增加,表面上的微凸體可能存在3種變形狀態(tài),分別為彈性變形、彈塑性變形和完全塑性變形。下面分別討論單個微凸體處于3種不同變形狀態(tài)時的接觸面積和接觸載荷。

2.2.1彈性變形狀態(tài)存在條件

根據(jù)Hertz理論[9],將開始塑性變形的臨界變形量為

(6)

式中，H為較軟材料的硬度,K為硬度系數(shù),與材料的泊松比v相關(guān),滿足K=0.454+0.41v,E為等效彈性模量,φ=H/E為材料屬性。

當(dāng)ω≤ωec時,微凸體發(fā)生彈性變形,由Hertz理論可得,單個微凸體的接觸面積a和接觸載荷F分別為

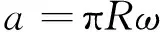
(7)

(8)

當(dāng)微凸體變形量為ωec時,可認(rèn)為微凸體處于彈性變形范圍內(nèi),由(7)式可知,微凸體的彈性臨界接觸面積為

(9)

對比(7)式和(9)式可得:當(dāng)ω≤ωec時,有a≤aec,即單個微凸體的接觸面積小于或等于彈性臨界接觸面積時發(fā)生彈性變形。

聯(lián)立(7)式和(8)式得單個微凸體發(fā)生彈性變形時,接觸載荷F與接觸面積a之間的關(guān)系為

(10)

由(10)式可知,單個微凸體發(fā)生彈性變形時,接觸載荷與接觸面積的3/2次方成正比。

2.2.2彈塑性變形狀態(tài)存在條件

Kogut等[4]研究了粗糙表面單峰接觸的力學(xué)特性,結(jié)果表明:當(dāng)ωec<ω≤110ωec時,接觸微凸體發(fā)生彈塑性變形,并將微凸體的彈塑性變形分為2個區(qū)域:

第一彈塑性變形區(qū)(ωec<ω≤6ωec)

(11)

第二彈塑性變形區(qū)(6ωec<ω≤110ωec)

(12)

易得第一彈塑性和第二彈塑性的臨界變形量分別為

(13)

(14)

將(6)式、(8)式和(9)式代入(11)式和(12)式中,可得單個微凸體發(fā)生彈塑性變形時,接觸載荷F與接觸面積a之間的關(guān)系為

(15)

(16)

式中，aepc和apc分別為第一彈塑性臨界接觸面積和第二彈塑性臨界接觸面積,其大小分別為aepc=7.119 7aec、apc=205.382 7aec由(15)式和(16)式可知,單個微凸體發(fā)生彈塑性變形時,接觸載荷與接觸面積近似成線性關(guān)系。

2.2.3完全塑性變形存在條件

當(dāng)ω>ωpc時,微凸體發(fā)生完全塑性變形,接觸面積a和接觸載荷F的表達(dá)式如下

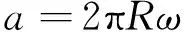
(17)

(18)

綜上所述,單個微凸體的臨界接觸面積(彈性臨界接觸面積、第一彈塑性臨界接觸面積和第二彈塑性臨界接觸面積)是尺度相關(guān)的,符合經(jīng)典赫茲接觸理論[7],與傳統(tǒng)的分形接觸模型不同。對于確定的材料屬性和分形參數(shù),微凸體臨界彈性接觸面積與微凸體的等級成反比。任一微凸體受力發(fā)生變形,接觸面積a滿足:a≤aec時為彈性變形;aecapc時為完全塑性變形。

2.3微凸體等級n的計算

當(dāng)δ≤ωec,微凸體發(fā)生彈性變形,即:

可求得彈性臨界等級為

(19)

式中，fix表示取整

同理可以得到第一彈塑性臨界等級nepc為

(20)

第二彈塑性臨界等級npc為

(21)

綜上所述,當(dāng)nmin≤n≤nec時,微凸體只發(fā)生彈性變形;當(dāng)necnpc時,微凸體發(fā)生彈性變形、第一彈塑性變形、第二彈塑性變形和完全塑性變形。

2.4微凸體的面積分布密度函數(shù)

Wang和Komvopoulos等[10]在修正的M-B分形接觸模型中指出,分形粗糙表面與剛性光滑平面接觸時,微凸體的接觸面積分布密度函數(shù)為

(22)

真實接觸面積Ar為

(23)

式中，al為最大微凸體的接觸面積,φ為分形區(qū)域擴展系數(shù),與輪廓分形維數(shù)D之間的函數(shù)表達(dá)式[8]為

(24)

2.5真實接觸面積和接觸載荷

兩粗糙表面接觸時的真實接觸面積Ar和總的接觸載荷Fr是所有接觸微凸體的接觸面積和接觸載荷的總和,計算如下

真實接觸面積為

(25)

式中，Are為彈性變形部分的接觸面積,Arep1為第一彈塑性變形部分的接觸面積,Arep2為第二彈塑性變形部分的接觸面積,Arp為完全塑性變形部分的接觸面積。下面分別計算這四部分的真實接觸面積。

(26)

(27)

(28)

(29)

總的接觸載荷為

(30)

同理,Fre為彈性變形部分接觸載荷,Frep1為第一彈塑性變形部分接觸載荷,Frep2為第二彈塑性變形部分接觸載荷,Frp為完全塑性變形部分接觸載荷。

(31)

(32)

(33)

(34)

將(31)～(34)式代入(30)式并進行無量綱化處理即兩邊同時除以EAa,可得總的接觸載荷與真實接觸面積之間的無量綱關(guān)系

(35)

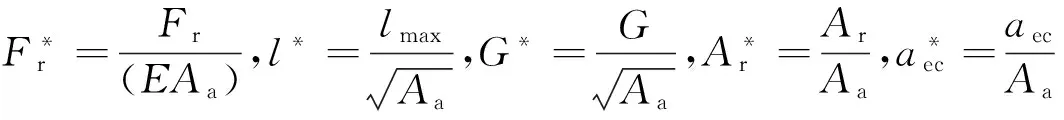
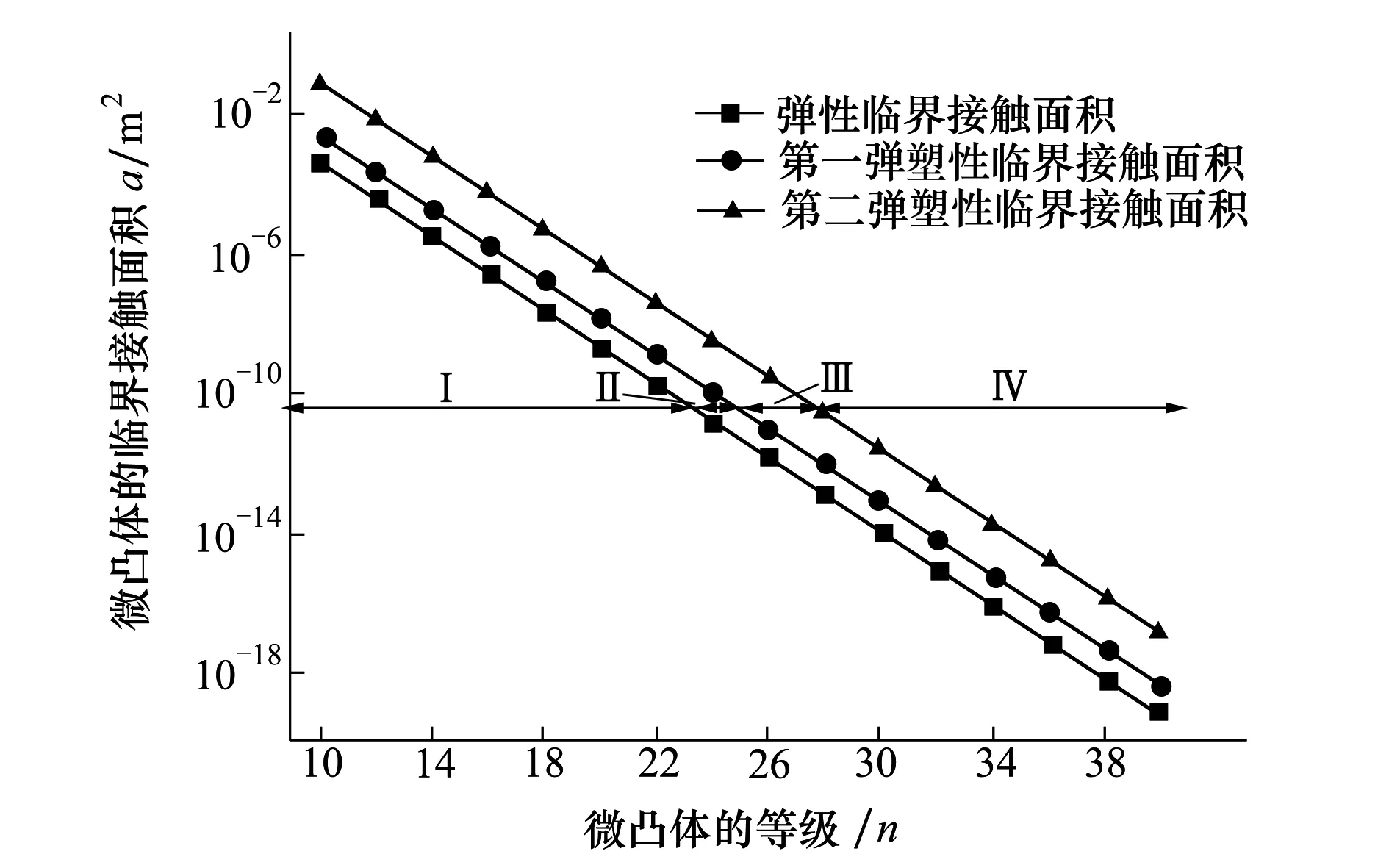
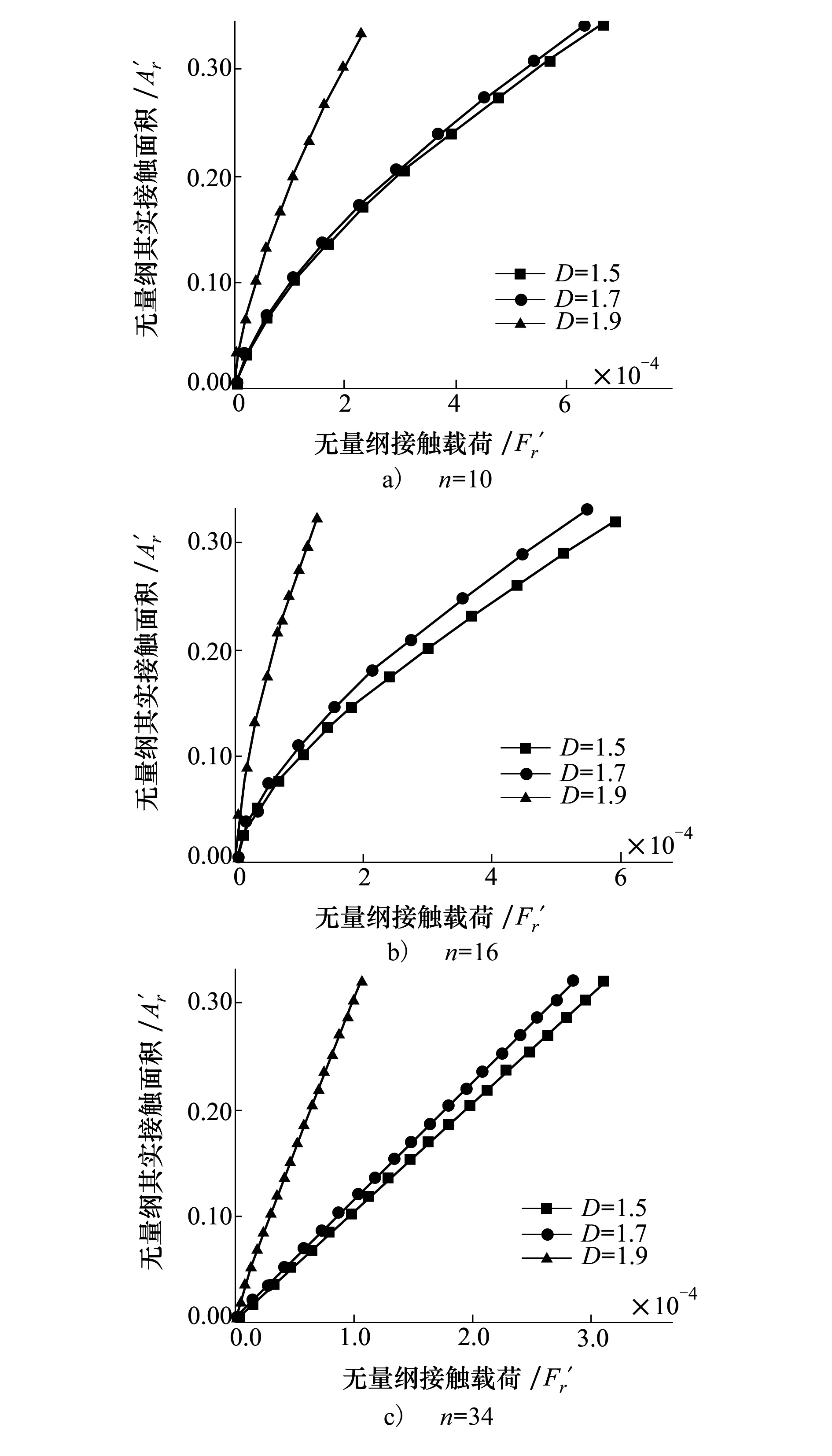
由于單個微凸體臨界接觸面積的尺度相關(guān)性,在求解真實接觸面積和接觸載荷過程中,臨界接觸面積選取影響結(jié)果的準(zhǔn)確性,在本文中我們選擇最大微凸體的臨界接觸面積(對應(yīng)等級n最小)來計算整個粗糙表面的接觸載荷和真實接觸面積,以下對其誤差進行分析。計算參數(shù)選取D=1.5,G=2.5×10-9m,φ=0.001。

1) 當(dāng)所有微凸體都處于同種變形狀態(tài)時,同時處于彈性變形狀態(tài)、第一彈塑性變形狀態(tài)、第二彈塑性變形狀態(tài)或完全塑性變形狀態(tài)。粗糙表面的真實接觸面積和接觸載荷可以用最大微凸體的臨界接觸接觸面積來計算[7]。

(36)

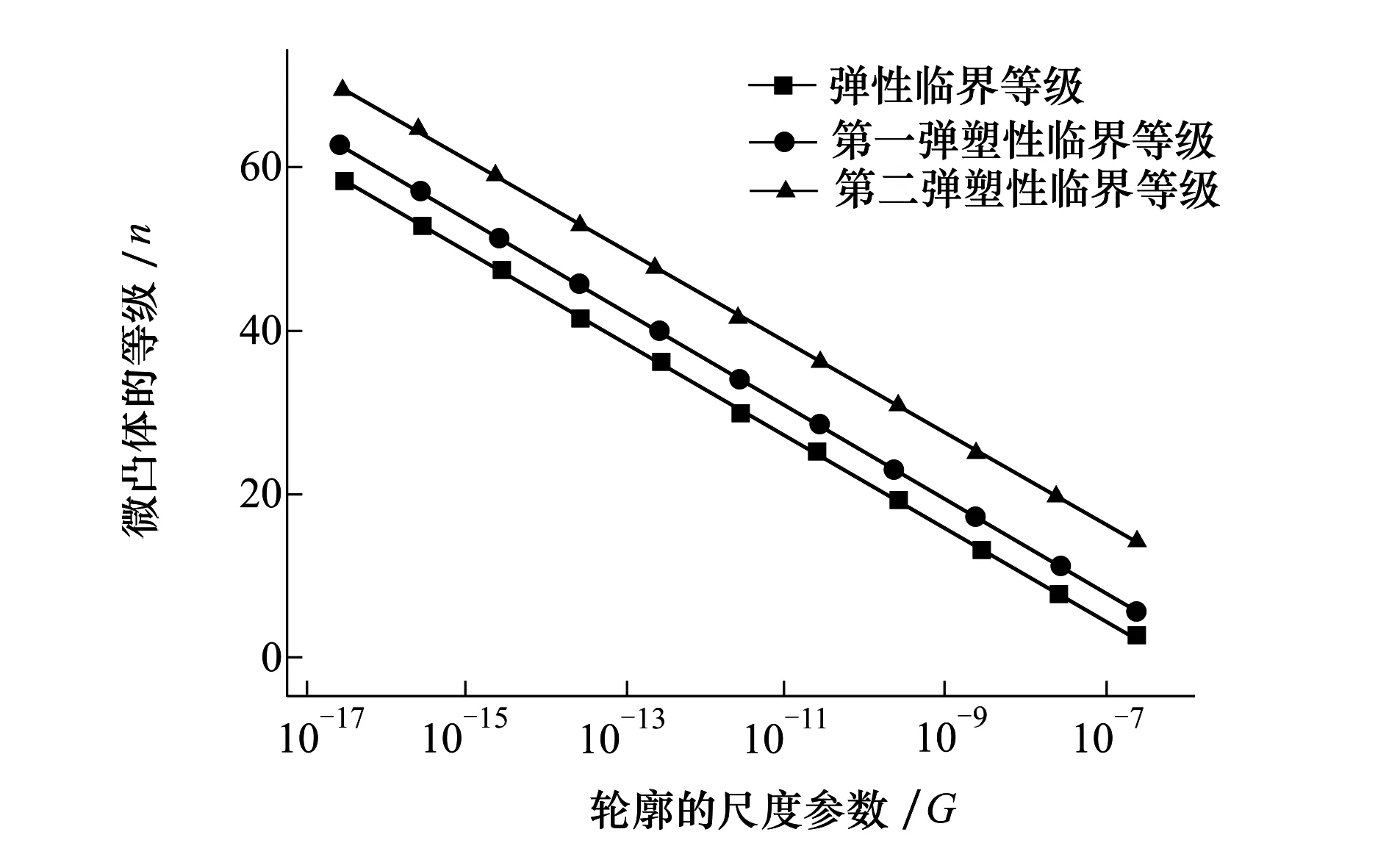
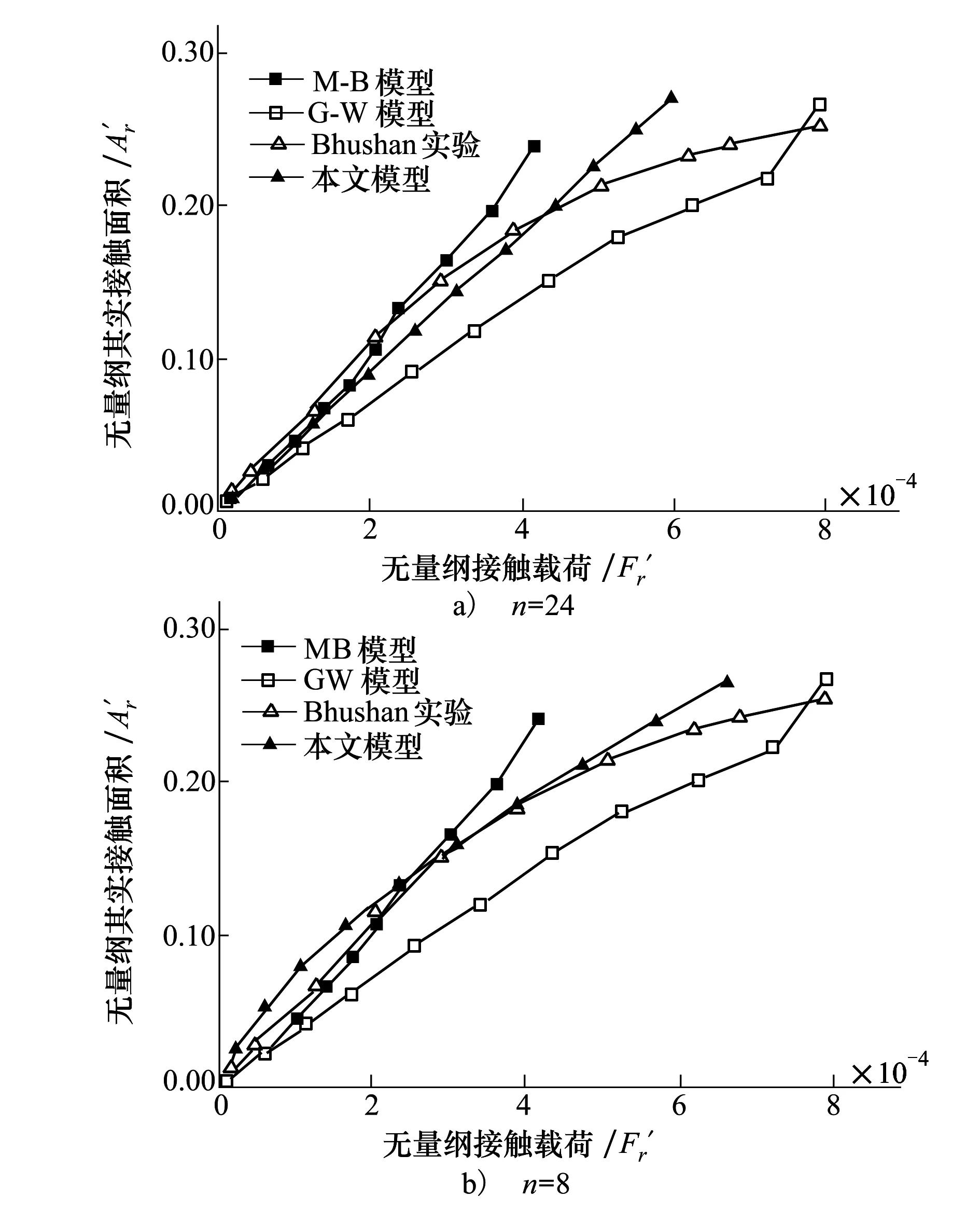
當(dāng)an≤anec,所有微凸都體處于彈性變形狀態(tài);當(dāng)anec

2)、當(dāng)微凸體處于不同變形狀態(tài)時,分為以下3種情況:

(1) 當(dāng)最大微凸體處于彈性變形狀態(tài)時,其余微凸體可能處于第一彈塑性變形狀態(tài)。以本文計算結(jié)果,真實接觸面積為

(37)

(38)

(39)

(2) 當(dāng)最大微凸體處于彈性變形狀態(tài)時,其余微凸體可能處于第二彈塑性變形階段。同理可得真實接觸面積的比值為:

(3) 當(dāng)最大微凸體處于彈性變形狀態(tài)時,其余微凸體可能處于完全塑形變形階段。同理可得真實接觸面積的比值為

式中，η表示選取不同微凸體所得到的真實接觸面積的比值,下標(biāo)1表示微凸體發(fā)生彈性變形和第一彈塑性變形,下標(biāo)2表示微凸體發(fā)生彈性變形、第一彈塑性變形和第二彈塑性變形,下標(biāo)3表示微凸體發(fā)生彈性變形、第一彈塑性變形、第二彈塑性變形和完全塑性變形。

為了說明我們選擇最大微凸體來計算真實接觸面積和載荷的合理性。我們又選擇了小一級和小兩級的微凸體,計算了其真實接觸面積的與最大微凸體真實接觸面積的比值。

經(jīng)過計算,選擇最大微凸體相鄰的微凸體得到的總的真實接觸面積與最大微凸體所得的真實接觸面積的比值都小于50%,為了獲得準(zhǔn)確的計算結(jié)果,可以用最大微凸體的臨界接觸面積來計算整個粗糙表面的真實接觸面積和載荷。

經(jīng)過誤差分析,在微凸體下壓量與微凸體高度比值相同的情況下,最大微凸體的接觸面積是最大的,因而粗糙表面中最大微凸體的力學(xué)性能直接決定整個粗糙表面的力學(xué)性能。當(dāng)最大微凸體發(fā)生彈性變形,即使較大等級的微凸體發(fā)生彈塑性變形,對其整個粗糙表面的真實接觸面積的影響很小,從工程應(yīng)用和保守計算角度分析,選取最大微凸體的臨界接觸面積計算整個粗糙表面的真實接觸面積和接觸載荷是合理的。

3數(shù)值仿真結(jié)果與分析

基于前文所推導(dǎo)出的計算結(jié)果,分析粗糙表面接觸過程中的真實接觸面積與微凸體總接觸載荷之間的關(guān)系。粗糙表面相關(guān)參數(shù)為:輪廓分形維數(shù)D分別取1.5、1.7、1.9,輪廓特征尺度系數(shù)取G=2.5×10-16～2.5×10-7,泊松比ν=0.3,材料的彈性模量E=2.3×1011N/m2,硬度為H=6.58×108N/m2。

圖2為微凸體的臨界接觸面積(彈性臨界接觸面積、第一彈塑性臨界接觸面積和第二彈塑性臨界接觸面積)與微凸體等級之間的關(guān)系。

圖2　微凸體的臨界接觸面積與等級之間的關(guān)系

粗糙表面的分形參數(shù)為D=1.5,G=2.5×10-9。其中:Ⅰ為彈性變形區(qū);Ⅱ為第一彈塑性變形區(qū);Ⅲ為第二彈塑性變形區(qū);Ⅳ為完全塑性變形區(qū)。在Ⅰ區(qū)域中,這些等級的微凸體只能發(fā)生彈性變形;在區(qū)域Ⅱ中,這些等級的微凸體可以發(fā)生彈性變形和第一彈塑性變形;在區(qū)域Ⅲ中,這些等級的微凸體可以發(fā)生彈性變形、第一彈塑性變形和第二彈塑性變形;在區(qū)域Ⅳ中,這些等級的微凸體可以發(fā)生彈性變形、彈塑性變形和完全塑性變形。從圖2中可以看出,當(dāng)表面的分形參數(shù)一定時,單個微凸體的臨界接觸面積aec,aepc,apc是變化的,是和微凸體的尺度相關(guān)的,隨著微凸體的等級n的增大而減小。對于確定等級的微凸體,隨著接觸面積的增大,微凸體先發(fā)生彈性變形,再發(fā)生彈塑性變形,最后發(fā)生完全塑性變形。

圖3為在輪廓的分形維數(shù)D=1.5的情況下,微凸體的臨界等級(彈性臨界等級、第一彈塑性臨界等級和第二彈塑性臨界等級)與輪廓的特征尺度參數(shù)之間的關(guān)系。由圖3可知,3種臨界等級都隨著輪廓尺度參數(shù)的增大而減小。在相同的特征尺度參數(shù)下,第二彈塑性臨界等級最大,彈性臨界等級最小,而第一彈塑性臨界等級介于這2種臨界等級之間。當(dāng)輪廓尺度參數(shù)G增大到一定值時,臨界等級小于零,但事實上,最大微凸體的等級大于零的,因此當(dāng)分形維數(shù)為D=1.5時,輪廓的特征尺度參數(shù)不能大于2.5×10-7m。

圖3　微凸體的臨界等級與輪廓特征尺度參數(shù)之間的關(guān)系

圖4　　　　無量綱接觸載荷與無量綱　　　真實接觸面積之間的關(guān)系

4與其他模型的比較

圖5　不同接觸模型與實驗對比

5結(jié)論

1) 分形粗糙表面中單個微凸體的臨界接觸面積aec,aepc,apc是和微凸體的尺度相關(guān)的,臨界接觸面積是由材料屬性和微凸體等級n共同決定。在確定的材料屬性條件下,單個微凸體臨界彈性接觸面積與微凸體等級成反比。

2) 材料屬性和分形參數(shù)一定時,粗糙表面上的接觸載荷與最大微凸體接觸面積和其對應(yīng)的臨界彈性接觸面積相關(guān),實際計算時,只要得到分形粗糙表面上最大微凸體接觸面積和其對應(yīng)的彈性臨界接觸面積就可獲得整個粗糙表面上的接觸載荷與真實接觸面積,避免對粗糙表面進行彈塑性及完全塑性的重復(fù)計算,簡化計算步驟。

3) 粗糙表面接觸過程中,最大微凸體所處的等級范圍不同,粗糙表面表現(xiàn)出來的力學(xué)性能也不相同。在整個粗糙表面接觸過程中,粗糙表面變形過程與單個微凸體的變形過程一致。接觸面積一定時,輪廓分形維數(shù)增大,接觸載荷減小。

參考文獻(xiàn)：

[1]Greenwood J A, Williamson J B P. Contact of Nominally Flat Surfaces[J]. Mathematical and Physical Sciences, 1966, 295(1442): 300-319

[2]Chang W R, Etsion I, Bogy D B. An Elastic-Plastic Model for the Contact of Rough Surfaces[J]. ASME Journal of Tribology, 1987, 109: 257-263

[3]Majumdar A, Bhushan B. Fractal Model of Elastic-Plastic Contact between Rough Surfaces[J]. ASME Journal of Tribology, 1991, 113: 1-11

[4]Kogut L, Etsion I. Elastic-Plastic Contact Analysis of a Sphere and a Rigid Flat[J]. ASME Journal of Applied Mechanics, 2002, 69(5): 657-662

[5]Morag Y, Etsion I. Resolving the Contradiction of Asperities Plastic to Elastic Mode Transition in Current Contact Models of Fractal Rough Surfaces[J]. Wear, 2007, 262(5/6): 624-629

[6]Jeng Luen Liou, Chi Ming Tsai, Lin Jenfin. A Microcontact Model Developed for Sphere-and Cylinder-Based Fractal Bodies in Contact with a Rigid Flat Surface[J]. Wear, 2010, 268: 431-442

[7]Miao Xiaomei, Huang Xiaodiao. A Complete Contact Model of a Fractal Rough Surface[J]. Wear, 2014, 309: 146-151

[8]丁雪興, 嚴(yán)如奇, 賈永磊. 基于基底長度的粗糙表面分形接觸模型的構(gòu)建與分析[J]. 摩擦學(xué)學(xué)報, 2014, 34(4): 341-347

Ding Xuexing, Yan Ruqi, Jia Yonglei. Construction and Analysis of Fractal Contact Mechanics Model for Rough Surface Based on Base Length[J]. Tribology, 2014, 34(4): 341-347 (in Chinese)

[9]Johnson K L. Contact Mechanics[M]. London: Cambridge University Press, 1985: 79-128

[10] Wang S, Komvopoulos K. A Fractal Theory of the Interfacial Temperature Distribution in the Slow Sliding Regime: PartⅡ——Multiple Domains, Elastoplastic Contacts and Applications[J]. ASME Journal of Tribology, 1994, 116(4): 824-832

[11] Bhushan B. The Real Area of Contact in Polymeric Magnetic Media-PartⅡ: Experimental Data Analysis[J]. ASLE Transactions, 1985, 28: 181-197

收稿日期：2015-10-27

基金項目：國家自然科學(xué)基金(51105304、51475364)與陜西省自然科學(xué)基礎(chǔ)研究計劃(2015JM5212)資助

作者簡介：成雨(1991—)，西安理工大學(xué)碩士研究生，主要從事接觸、摩擦理論方法研究。

中圖分類號：TH117

文獻(xiàn)標(biāo)志碼：A

文章編號:1000-2758(2016)03-0485-08

The Elastic-Plastic Contact Mechanics Model Related Scale of Rough Surface

Cheng Yu1, Yuan Yuan1, Gan Li1, Xu Yingqiang2, Li Wanzhong2

1.School of Mechanical and Precision Instrument Engineering, Xi′an University of Technology, Xi′an 710048, China 2.School of Mechanical Engineering, Northwestern Polytechnical University, Xi′an 710072, China

Abstract:The real contact state between the rough surfaces is studied with fractal theory, a fractal contact mechanics model for rough surfaces is proposed also. Considering the asperity level, the expressions among elastic critical level, the first elastic-plastic critical level and the second elastic-plastic critical level are obtained. The conditions existence of elastic deformation, elastic-plastic deformation and fully plastic deformation of each level asperity are researched on the rough surface, the expressions among the critical contact area in the three regimes are derived respectively. Considering the asperity size distribution function, the analytic expression between the total contact load with the real contact area is obtained. Calculation results show that the critical contact areas of a single asperity are related to its scale, and its reduce while the level of asperity increases. As the load and contact area increase a transition from elastic, elastic-plastic to fully plastic contact model takes place in this order and agreed with classical contact mechanics. During the whole rough surfaces contact, the deformation process of the rough surfaces is consistent with a single asperity. The largest asperity is in different critical levels, mechanical properties of the rough surface are not the same.

Keywords:rough surfaces; asperity; fractal dimension; scale; critical contact area; elastic-plastic contact; density function; two dimensional; topology; models analysis; mechanical properties; deformation; friction