不同采樣間隔的鐘差數據對鐘差預報的影響分析

王　寧，呂志平，王宇譜，宮曉春，孫大雙

(信息工程大學 地理空間信息學院，河南 鄭州 450001)

?

不同采樣間隔的鐘差數據對鐘差預報的影響分析

王寧，呂志平，王宇譜，宮曉春，孫大雙

(信息工程大學 地理空間信息學院，河南 鄭州 450001)

摘要：在衛星導航定位系統中，星載原子鐘的鐘差預報在維持系統時間同步、滿足實時精密單點定位的需求等方面具有重要的作用。目前，鐘差預報主要研究的是預報模型，關于鐘差數據對鐘差預報結果影響的研究還很少。基于IGS提供的30 s、5 min和15 min采樣間隔的精密鐘差數據，分析和研究在預報條件相同時，不同采樣間隔的鐘差數據對鐘差預報效果的影響。以常用的灰色模型和二次多項式模型對不同類型的衛星鐘差進行預報和分析，結果表明,相同預報條件下鐘差數據的采樣率對預報結果有影響，IGS的15 min采樣間隔的精密鐘差數據較另外兩種采樣間隔的精密鐘差數據能得到更好的預報結果。

關鍵詞：衛星鐘差預報；數據采樣間隔；預報精度；預報耗時

GPS單點定位的精度受到許多誤差的影響，如衛星軌道誤差、衛星鐘差、大氣層延遲、接受機鐘差及多路徑效應[1]。在各類誤差中，衛星鐘差是影響定位精度的重要因素；在實時GPS導航定位中，GPS衛星鐘差預報是實現GPS高精度實時應用的關鍵技術之一[2-3]。

目前，國內外學者建立了多種鐘差預報模型，其中較為常用的預報模型主要是二次多項式(QP)模型和灰色系統模型(GM(1,1))[4-5]。在現有的關于預報模型的預報效果研究中，由于IGS(International GNSS Service)提供3種不同采樣間隔的精密鐘差數據(30 s、5 min、15 min采樣間隔)，因此，不同的研究人員采用不同采樣間隔的鐘差數據進行預報試驗，使得對模型預報效果的分析存在一定程度的差異。本文旨在基于兩種常用模型，探討不同采樣間隔的鐘差數據對預報模型及其預報效果的影響，得到一些有益的結論為鐘差預報的研究提供參考。

1兩種常用鐘差預報模型的表達式

1.1二次多項式模型

二次多項式模型其對應的誤差方程[6-7]為

(1)

其中:Li為ti時刻的衛星鐘鐘差，t0為參考時刻，ti為歷元時刻；待估參數a0,a1和a2分別表示參考時刻t0時的衛星鐘差、鐘速及衛星鐘的頻漂。根據最小二乘平差原理，當已知鐘差數據多于3個時，解得參數最或然值則得鐘差預報的QP模型為[8]

(2)

1.2灰色系統模型

設L(0)={l(0)(i),i=1,2,…,n}為不同歷元的鐘差值，則鐘差的灰色模型表達式為[9-10]

(3)

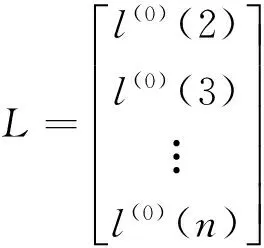
2試驗與分析

使用GPS系統30 s、5 min、15 min采樣間隔的

最終精密鐘差產品進行預報試驗。以2014-07-20—2014-07-26共7 d的鐘差數據為例(其它時間段的數據亦可)，同時考慮此時間段的星載原子鐘包括BLOCK ⅡA銫鐘、BLOCK ⅡA銣鐘、BLOCK ⅡR銣鐘、BLOCK ⅡR-M銣鐘、BLOCK ⅡF銫鐘、BLOCK ⅡF銣鐘6種類型，隨機選取該時間段內不存在鐘差跳變和間斷、數據完整的每類鐘的一顆衛星進行試驗[12]。本文選取的是PRN01、PRN10、PRN22、PRN24、PRN29、PRN32這6顆衛星。

預報試驗中，以預報所對應的已知IGS精密鐘差數據作為參考真值，使用均方根誤差(RMS)、極差(最大誤差與最小誤差之差的絕對值，記為Range)以及程序的耗時作為統計量，分析預報效果，其中均方根誤差的計算公式為

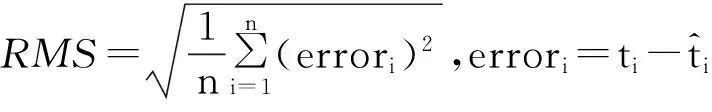
(4)

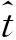
分別采用QP模型和GM(1,1)模型，使用一周的鐘差數據進行連續6 d的鐘差預報，具體的實驗方案如下：

方案1：2014-07-20的鐘差數據建模，預報2014-07-21的鐘差；

方案2：2014-07-21的鐘差數據建模，預報2014-07-22的鐘差；

方案3：2014-07-22的鐘差數據建模，預報2014-07-23的鐘差；

方案4：2014-07-23的鐘差數據建模，預報2014-07-24的鐘差；

方案5：2014-07-24的鐘差數據建模，預報2014-07-25的鐘差；

方案6：2014-07-25的鐘差數據建模，預報2014-07-26的鐘差。

2種常用模型下各實驗方案預報結果的統計值如表1、表2所示。

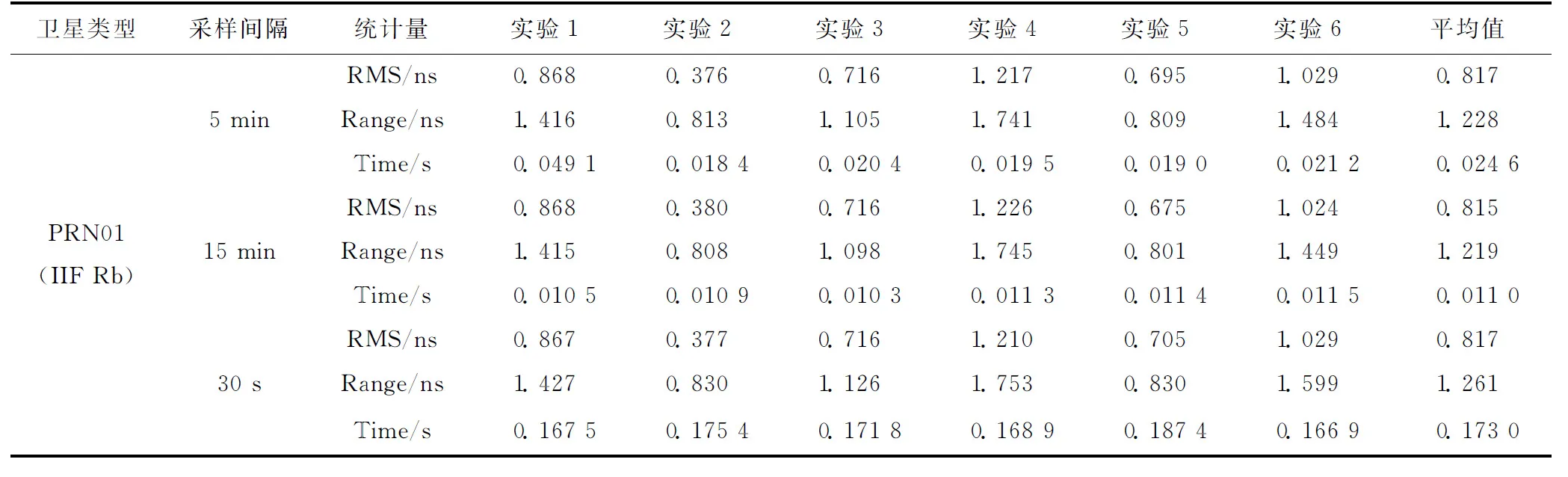
表1　GM(1,1)模型下6種方案的預報結果統計值

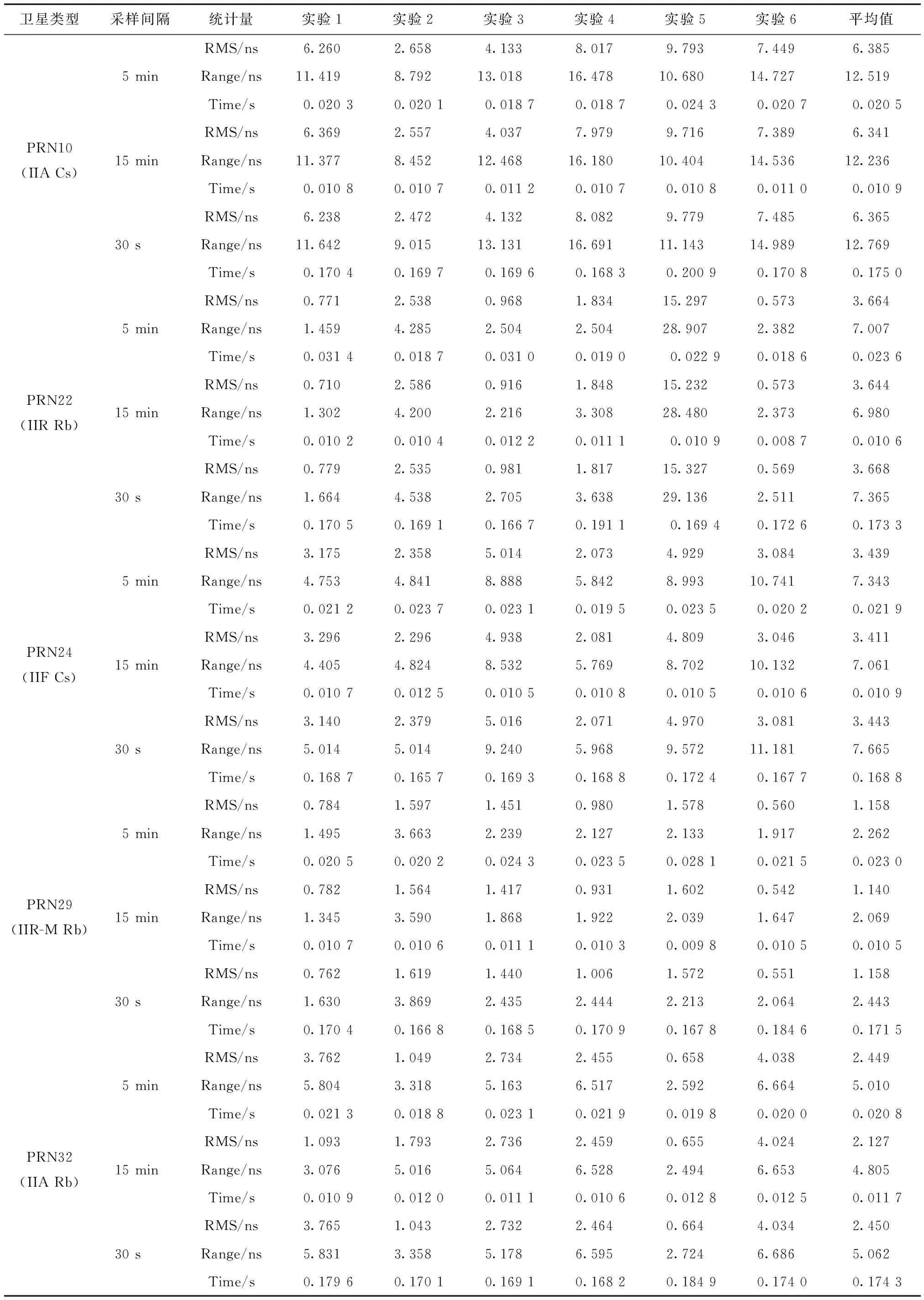
續表1

表2　QP模型下6種方案的預報結果統計值

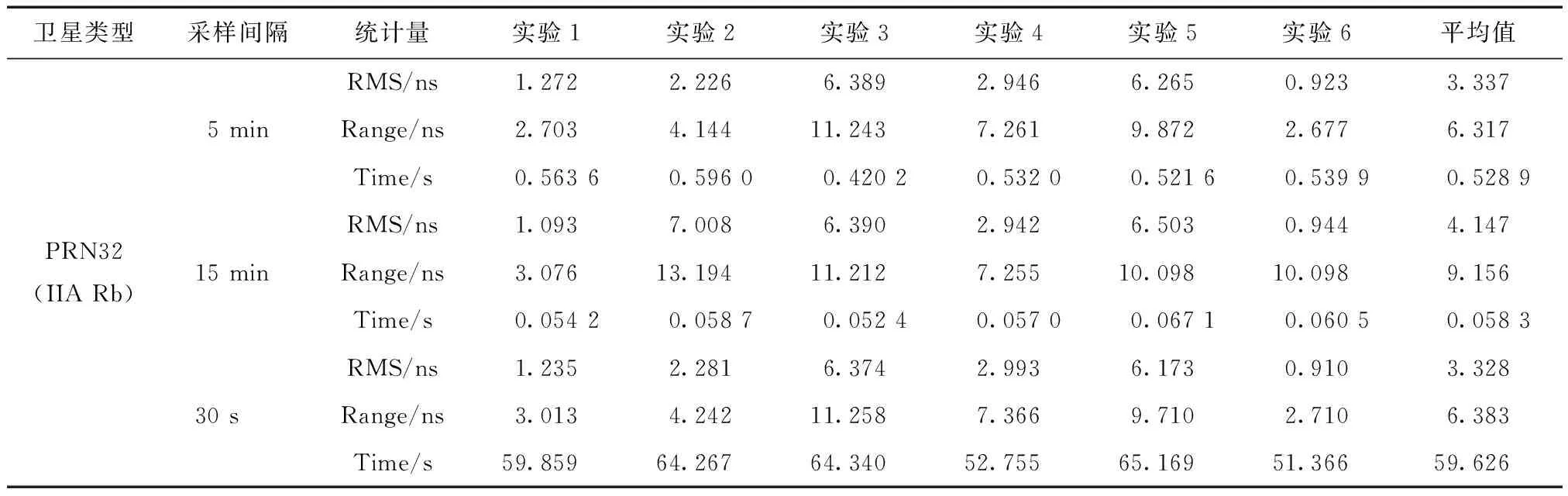
續表2

根據表1、表2中不同星載原子鐘的預報結果，統計出在RMS和Range統計量下不同采樣間隔數據在同一實驗中預報精度最高的次數，整理如表3所示。同時對3種采樣間隔的數據在2種鐘差預報模型下的平均耗時整理至表4。

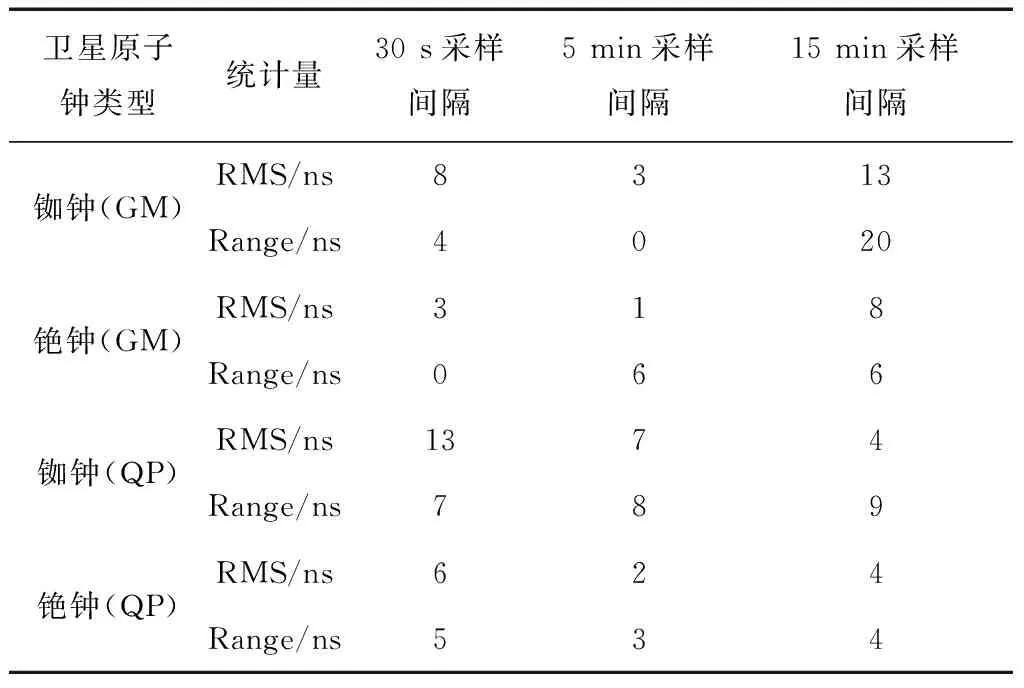
表3　各實驗精度最高出現的次數

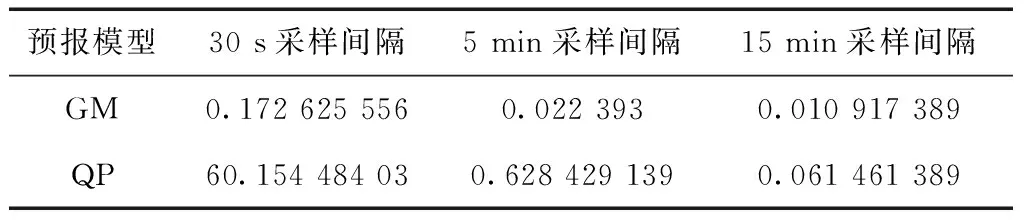
表4　預報耗時平均值　s

1)表3的第2、3行為星載原子鐘為銣鐘的PRN01、PRN22、PRN29、PRN32的實驗數據，從統計結果可以看出：用GM模型對銣鐘進行鐘差預報時，從預報精度角度看，15 min采樣間隔的數據進行建模預報獲得精度最高的次數最多；從預報結果的穩定性來看，使用15 min采樣間隔數據進行鐘差預報所得結果相對穩定。表3的第4、5行為星載原子鐘為銫鐘的PRN10、PRN24的實驗數據，從統計結果可以看出：用GM模型對銫鐘進行鐘差預報時，采用15min采樣間隔數據進行建模預報時在RMS統計量下精度最高的次數最多且優勢明顯，但在Range統計量下和5 min采樣間隔預報精度最高的次數相當。

2)表3的第5、6行為星載原子鐘為銣鐘的PRN01、PRN22、PRN29、PRN32的實驗數據，用QP模型對銣鐘進行預報，采用30 s采樣間隔的數據進行建模預報時在RMS統計量下預報精度最高的次數最多，在Range統計量下15 min采樣間隔數據精度最高的次數最多。表3的第7、8行為星載原子鐘為銫鐘的PRN10、PRN24的預報數據，從上表可以看出：用QP模型對銫鐘進行預報時，從預報精度角度看，30 s采樣間隔的數據進行建模預報獲精度最高的次數最多。

3)分析表1時間統計量的每一行和表4的第2行可知，在GM模型下，15 min采樣間隔數據建模預報的耗時最少；5 min采樣間隔的耗時大約是15 min采樣間隔的2倍；而30 s采樣間隔的耗時則為15 min采樣間隔的10倍以上，平均耗時達到15倍。由此可見，15 min采樣間隔數據的建模預報效率最高。

4)分析表2時間統計量的每一行和表4的第2行可知，在QP模型下，15 min采樣間隔數據建模預報的耗時最少；5 min采樣間隔的耗時大約是15 min采樣間隔的10倍；30 s采樣間隔的耗時為15 min采樣間隔的940倍以上，平均耗時達到978倍。從預報耗時角度看，15 min采樣間隔的數據進行建模預報可大大提高預報的效率。

5)對比表1的最后一列可以得出：在GM模型中，分析RMS和Range統計量的平均值可知采用15 min采樣間隔的數據進行建模預報，在這兩個統計量下建模預報精度最高的次數都是最多的；對比表2的最后一列可以得出：在QP模型中，30 s采樣間隔的數據在RMS統計量下預報精度最高，在6次實驗中精度最高的次數達到5次，但在Range統計量下正好相反；15 min采樣間隔的數據得出的結果比較穩定，5 min采樣間隔的數據得到的結果最差。

3結束語

針對常用的鐘差預報模型(二次多項式模型和灰色系統模型)，實驗選取了不同原子鐘在不同時段的鐘差數據，分別研究了不同采樣間隔的精密鐘差數據對鐘差預報精度的影響，為衛星鐘差預報研究提供借鑒與參考。

從實驗分析可以看出：在GM模型下，采用15 min采樣間隔的IGS精密鐘差數據得出的精度最高，建模速度和預報速度最快，其效率比5 min采樣間隔提高2倍，比30 s采樣間隔提高15倍。原因如下：①15 min采樣間隔的數據是IGS鐘差產品中精度最高的數據，數據量小但能取得較好的數學模型。②灰色模型的特點是用少量數據建模，并非原始建模數據越多，預報精度越高。因此，在采用GM模型進行衛星鐘差預報時盡量采用15 min采樣間隔的鐘差數據建模預報，這樣可以有效提高建模和預報精度；在QP模型的鐘差預報實驗當中，從預報精度分析，30 s采樣間隔的IGS精密鐘差數據在RMS統計量下得出的精度最高，但在Range統計量下15 min采樣間隔的預報精度比較穩定；從預報耗時角度分析，15 min采樣間隔的數據建模速度和預報速度最快，其效率比5 min采樣間隔提高10倍，比30 s采樣間隔提高可達978倍。其原因是：a.30 s采樣間隔的數據比較密，有利于QP模型的擬合，因此，在RMS統計量下預報精度比較高；b.30 s采樣間隔的數據量比較大，而QP模型中數據處理的次數又比較多，所以利用30 s采樣間隔數據預報的耗時遠遠高于15 min采樣間隔的數據。從實驗結果分析可以得出，在利用QP模型進行鐘差預報時，若單純追求RMS的精度，采用30 s采樣間隔的數據進行建模預報較好；但從RMS、Range這2種統計量和預報耗時的綜合影響角度來分析，采用15 min采樣間隔的數據更好。

參考文獻：

[1]劉基余.GPS衛星導航定位原理與方法[M].北京：科學出版社，2008：378.

[2]XU Guochang.GPS theory，algorithms and application[M],Germany:springer，2007:76-77.

[3]HEO Y J，CHO J，HEO M B.Improving prediction accuracy of GPS satellite clocks with periodic variation behavior[J].Measurement Science and Technology，2010，21(7)：3001-3008.

[4]王宇譜,呂志平,陳正生,等.衛星鐘差預報的小波神經網絡算法研究[J].測繪學報,2013,42(3):20-28.

[5]喜文飛，史正濤.基于卡爾曼濾波的動態灰色理論模型研究[J].測繪工程，2014,23(3):24-27.

[6]王繼剛.基于GPS精密單點定位的時間比對與鐘差預報研究[D].西安：中國科學院研究生院,2010.

[7]王金龍，蘭孝奇，高奮生.多項式擬合法和電離層殘差法聯合探測與修復周跳[J].測繪工程，2013,22(1):25-27.

[8]WANG J G，HU Y H，HE Z M，et al.Prediction of clock errors of atomic clocks based on modified linear combination model[J].Chinese Astronomy and Astrophysics，2011，35:318-326.

[9]崔先強,焦文海.灰色系統模型在衛星鐘差預報中的應用[J].武漢大學學報(信息科學版)，2005,30(5):447-450.

[10] 王宇譜,呂志平,陳正生,等.基于灰色模型與小波神經網絡的衛星鐘差預報方法[J].大地測量與地球動力學,2014,34(2):132-136.

[11] 楊富春，黃張裕，賈瑩媛，等.基于GM(1,1)灰色模型衛星鐘差短期預報的精度分析[J].測繪工程，2012,21(5)：25-29.

[12] 王宇譜,呂志平,陳正生,等.一種新的導航衛星鐘差預報與內插方法[J].大地測量與地球動力學,2013,33(4):112-116.

[責任編輯：劉文霞]

The effects of different sampling interval satellite clock bias data on the prediction

WANG Ning，LYU Zhiping，WANG Yupu，GONG Xiaochun，SUN Dashuang

(School of Surveying and Mapping，Information Engineering University，Zhengzhou 450001,China)

Abstract：Satellite clock bias (SBC) prediction of the space-borne atomic clock has an important role in satellite navigation system, such as maintaining the system time synchronization and meeting the needs of real-time precise point positioning. At present, the main study of the satellite clock bias is mainly focus on prediction models, but the effect of the clock bias data on the clock bias prediction is seldom concerned. By using 30s, 5min and 15min sampling intervals of precision clock bias products from IGS, the effect of clock bias prediction with GM(1,1) model and QP model under different sampling rates of clock bias data is studied in this paper. The test results show that the different sampling intervals of clock bias data have effects on the prediction results, and moreover the 15min sampling interval of precision clock bias data from the IGS can get better prediction results than that of the other two sampling intervals.

Key words：satellite clock bias (SCB) prediction；data sampling interval；precision of the prediction；time consuming of prediction

DOI:10.19349/j.cnki.issn1006-7949.2016.09.005

收稿日期：2015-04-30

基金項目：國家自然科學基金資助項目(41274015)；國家863計劃資助項目(2013AA122501)

作者簡介：王寧(1991-)，男，碩士研究生.

中圖分類號：P228

文獻標識碼：A

文章編號：1006-7949(2016)09-0020-06