兆瓦級風電機組傳動鏈動力學建模及仿真方法研究

劉樺，鄧良，陽小林

（東方電氣風電有限公司，四川德陽，618000）

?

兆瓦級風電機組傳動鏈動力學建模及仿真方法研究

劉樺，鄧良，陽小林

（東方電氣風電有限公司，四川德陽，618000）

摘要：以某兆瓦級風電機組為例，根據德國勞埃德2010版風機認證規范要求，繪制了機組傳動鏈動力學拓撲圖，建立了包含多自由度剛柔部件的機組傳動鏈模型。根據傳動鏈模型，進行了頻域分析，得到了機組傳動鏈模態頻率，繪制了二維Campbell圖，找到了傳動鏈潛在共振點，并通過時域掃頻分析，驗證了共振點的分析結果。與Bladed結果進行比較，驗證了仿真分析結果的正確性。

關鍵詞：兆瓦級風電機組，傳動鏈，動力學仿真

1　前言

風力發電機組是風能領域的一種旋轉能源機械，其動力學特性主要由機組的傳動鏈特性決定。掌握風電機組傳動鏈運動特性，是進行機組振動分析及控制設計等工作的重要基礎；同時，通過對運行工況的時域分析，可以考察機組運動和部件受力情況，對了解機組運動及部件設計有幫助，因此傳動鏈動力學分析是風電機組設計中一項重要工作。

對于小型風電機組，其傳動鏈動力學特性主要受傳動鏈部件的質量、轉動慣量、剛度和阻尼等因素影響，而隨著近十年來風電機組單機功率和部件尺寸的不斷增大，部件的柔性及傳動鏈支承特性對傳動鏈動力學特性的影響也逐漸明顯，因此在兆瓦級風電機組傳動鏈模型仿真分析中，必須予以考慮。近年來，國內外對兆瓦級風電機組傳動鏈建模做了較多研究。

荷蘭能源研究中心（ECN）采用通用多體動力學軟件對風電機組變槳系統、傳動鏈系統進行了仿真建模分析［1］。模型包含柔性葉片和塔架、傳動鏈、齒輪箱、齒輪箱支承以及外部氣動力輸入等單元，模擬了機組運行轉速、功率、變槳角、葉根載荷、部件變形以及其他機組部件運行動態數據，通過與測試數據對比，驗證了模型的正確性，相較于單獨的部件分析，由于考慮了部件之間的相互影響，其結果更具有可靠性。

德國Technical University of Dresden的Berthold Schlecht等采用多體動力學軟件對風電機組傳動鏈模型進行了時域和頻域仿真分析，除了模擬機組運行時的運動及載荷時序數據，同時也計算了機組傳動鏈的頻率結果，并分析了各個部件模態之間的相互影響和模態能量分布特征，為機組振動分析和控制設計提供了參考［2］。

德國Rwth Acchen Unverstiy的Schelenz等采用風機傳動鏈模型模擬了不同氣動模型對機組動態特性的影響［3］；Stuttgart University的Hauptmann等研究了采用風機傳動鏈模型與Matlab聯合仿真，進行機組控制系統設計的方法［4］。

2　風電機組傳動鏈模型的建立

機組傳動鏈模型的建立首先需要繪制傳動鏈拓撲圖，其次進行傳動鏈部件建模，并確定模型力元參數，然后綜合建立整個機組傳動鏈模型。

以某雙饋風電機組為例，其單機功率達到2.5 MW，風輪直徑超過100 m，機組安裝的大尺寸葉片、主軸以及齒輪箱等部件的柔性將顯著改變機組傳動鏈動力學特性，此外齒輪箱和電機支承的剛度和阻尼也會對機組傳動鏈動力學特性造成明顯的影響。因此必須建立符合兆瓦級風電機組傳動鏈動力學特性的剛柔耦合傳動鏈模型，并采用正確的分析方法進行仿真分析，才可以得到反映機組實際情況的結果。

2.1風電機組傳動鏈拓撲圖

機組傳動鏈模型的拓撲圖表示組成傳動鏈各個部件之間的運動和受力的樹型關系。繪制拓撲圖，可以分析傳動鏈部件運動和受力關系，還可以定義部件之間的自由度數目和類型，以及部件間相互作用力元類型、作用點和大小等關鍵建模元素。因此繪制傳動鏈模型拓撲圖是分析傳動鏈模型部件運動關系的重要工具，也是建立總體模型的基礎。

以前述雙饋風電機組為例，該機組傳動鏈屬于常規兩點支承布局，齒輪箱與電機通過高速軸聯軸器連接，齒輪箱和電機通過彈性支承安裝在機架上。根據機組傳動鏈模型的復雜程度，繪制的拓撲圖分為機組傳動鏈拓撲圖和齒輪箱拓撲圖，機組傳動鏈拓撲結構圖如圖1所示。

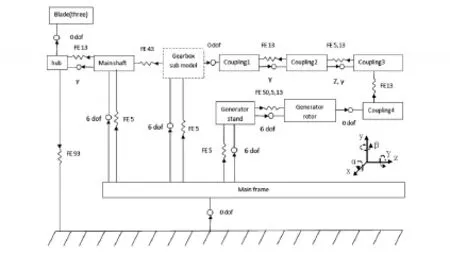
圖1　機組傳動鏈拓撲結構圖

如圖1所示，機組傳動鏈模型由所有傳遞扭矩的部件組成，包括葉片、輪轂、主軸、主軸軸承、齒輪箱、高速軸聯軸器、電機，以及齒輪箱和電機的彈性支承等。其中由于塔筒及機架對傳動鏈動力學特性的影響可忽略不計，因此模型中略去塔筒，將機架設置為剛體，并與大地坐標系固連。

大地坐標系的z軸平行于水平面，并指向風輪下風向方向，y軸垂直向上，x軸與y軸和z軸構成右手坐標系。圖中的“α”為繞x軸的旋轉方向；“β”為繞y軸旋轉方向；“γ”為繞z軸旋轉方向。

在機組傳動鏈拓撲圖中，葉片與輪轂固接；輪轂與主軸之間有γ方向旋轉自由度，通過表示輪轂扭轉剛度的力元連接；主軸相對于機架具有6個自由度，通過主軸軸承剛度矩陣力元安裝在機架的軸承座上，此外主軸與齒輪箱通過彈簧阻尼力元連接，表示主軸與齒輪箱之間的脹套連接；齒輪箱相對于機架也具有6個自由度，通過齒輪箱彈性支承剛度矩陣力元安裝在機架上；齒輪箱與高速軸聯軸器固接，高速軸聯軸器采用4個由彈簧阻尼力元連接剛體表示，剛體之間具有前后方向和γ方向自由度，表示聯軸器的縱向、橫向和扭轉運動；聯軸器與發電機轉子固連，發電機轉子具有6個自由度，通過電機軸承剛度矩陣力元安裝在發電機定子上；電機定子同樣具有6個自由度，通過電機彈性支承安裝在機架上，以此組成完整的機組傳動鏈拓撲圖。

在傳動鏈拓撲圖中，齒輪箱作為1個子結構表示，由于其內部具有復雜的軸系和齒輪動力學關系，因此需要單獨建立齒輪箱子模型。風電機組齒輪箱包括齒輪箱箱體、低速級行星架、主軸脹套連接、低速級內齒圈、低速級行星輪、低速級太陽輪、中速級輸入軸、中速級行星架、中速級內齒圈、中速級行星輪、中速級太陽輪、高速級輸入軸、高速級大齒輪軸、高速級大齒輪、高速級小齒輪軸和高速級小齒輪等部件。各級行星架、高速級大齒輪和小齒輪等部件具有6個自由度，通過軸承剛度矩陣力元安裝到齒輪箱箱體，各個齒輪副的嚙合力由嚙合力元表示。

2.2風電機組傳動鏈部件建模

傳動鏈模型中的部件建模根據其柔性對傳動鏈動力學特性影響的程度分為柔性部件建模和剛性部件建模。

本文采用德國勞埃德2010版風電機組認證規范［5］的建議進行分類，如表1所示。

對于剛體部件，需要給出部件模型的質量、轉動慣量和質心位置參數；對于柔性體部件，除了以上參數外，還需要對部件進行模態分析，將結果導入部件模型，完成柔性體部件建模；軸承采用支承剛度矩陣力元表示；傳動鏈彈性支承用彈簧阻尼力元表示。

由于篇幅所限，以下以輪轂和葉片為例，簡要說明剛體和柔性體部件的建立過程。

表1　傳動鏈部件處理方式

輪轂材料為QT350，為塑性鑄鐵材料［6］。輪轂剛體模型參數可由測量得到或從實體模型中讀出。此外需要考慮輪轂扭轉剛度對傳動鏈特性的影響，可以根據輪轂有限元模型在單位載荷下輪轂的角位移量計算得到。計算輪轂剛度的有限元模型［7］如圖2所示。

圖2　輪轂扭轉變形結果圖

機組的葉片采用復合材料制成，材料屬性為各向異性，因此采用含有葉片參數的數據表給出所需部件模型數據，如表2所示。

表2　葉片建模數據表

根據表2的葉片數據，建立葉片有限元模型進行模態分析，將結果讀入葉片模型中，完成葉片柔性體的建立。葉片外形如圖3所示。

圖3　葉片模型

單只葉片的質量為11 636 kg，葉片一階拍動和揮舞頻率分別為0.64 Hz和1.18 Hz，葉片二階拍動和揮舞頻率分別為1.81 Hz和3.60 Hz。

機組傳動鏈模型中的齒輪箱名義速比為84.5，采用常規的兩級行星輪和一級平行輪布局。建立完成的齒輪箱仿真模型如圖4所示。

圖4　齒輪箱模型

齒輪箱模型中，齒輪箱箱體、低速級和中速級行星架、所有齒輪軸處理為柔性體，低速級和中速級行星輪處理為剛體，軸承處理為剛度矩陣力元。

齒輪箱箱體通過齒輪箱彈性支承剛度和阻尼力元安裝到剛性機架。行星架和所有齒輪軸通過軸承剛度矩陣力元安裝在箱體內對應的各個軸承安裝孔的中心。各個齒輪副之間的嚙合力通過嚙合力元模擬。

齒輪箱的柔性部件建模過程與葉片柔性體建模過程基本一致，即首先建立部件有限元模型，然后進行模態分析，最后將模態分析結果導入到部件模型中，完成柔性部件建模。

齒輪箱柔性部件模型中都設置一個鉸接點，部件通過該鉸接點與其他部件相連，并給定自由度。此外，在軸承、花鍵和齒輪中心處設置Mark?er點，用于連接軸承剛度矩陣力元、花鍵力元以及齒輪副嚙合力元。

各個部件的有限元模型如圖5所示。

圖5　齒輪箱各部件有限元模型

在機組傳動鏈中，高速軸聯軸器是連接電機與齒輪箱高速軸的部件。傳動鏈仿真模型中，將聯軸器處理為4段由彈簧和阻尼連接的剛體組成，如圖6所示。

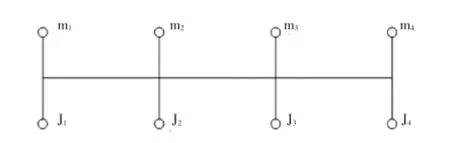
圖6　高速軸聯軸器參數圖

其中，圖中m1為第1段剛體質量，對應的m2、m3和m4為第2、3和4段剛體質量，兩段剛體之間通過1個扭轉彈簧連接，表示聯軸器的扭轉剛度。此外，為了表示聯軸器軸向剛度，在聯軸器第2段與第3段剛體之間設置1個平動剛度彈簧，表示聯軸器軸向方向的剛度。

在傳動鏈仿真模型中，將發電機處理為電機轉子、電機定子、電機彈性支承和電機軸承組成。電機轉子通過電機軸承剛度矩陣力元安裝到電機定子，電機定子通過電機彈性支承剛度力元安裝在剛性機架上。在模型仿真分析中，由于電機轉子和定子對傳動鏈動力學特性影響可以忽略，因此模型中將兩者都簡化處理為剛體。

2.3傳動鏈模型力元的確定

在機組傳動鏈模型中，部件之間有力元作用，如軸承剛度矩陣力元、彈簧力元、扭轉力元、齒輪副嚙合力元，以及外部時間激勵力元等。它們的類型及參數對傳動鏈動力學特性有很大影響，因此必須在傳動鏈模型中確定。對于某些力元，如軸承的剛度矩陣力元，可以參考軸承在不同受力情況下，各個方向的剛度數據給定。另外一些力元由于缺乏參數值，則需要根據力學公式計算確定。如齒輪箱彈性支承和電機彈性支承力元的阻尼值，以及高速軸聯軸器彈簧阻尼力元等。

對于齒輪箱彈性支承，根據力元不同平動方向的剛度和阻尼因子數據，以及齒輪箱彈性支承中心距離齒輪箱輸入軸中心距離計算出力元的阻尼值。首先計算齒輪箱轉動慣量，包括葉片、輪轂、主軸和齒輪箱箱體慣量，然后根據彈性支承力臂長度，計算齒輪箱等效質量，最后根據振動力學，阻尼值計算見式（1）。

式中：D為阻尼因子；K為單個彈性支承線性剛度；n為彈性支承個數。求出代表齒輪箱彈性支承的彈簧阻尼力元的阻尼值。

發電機彈性支承和高速軸聯軸器的彈簧阻尼力元的計算過程類似，這里不再贅述。表3、表4分別為計算得到彈性支承力元和高速軸聯軸器力元剛度和參數值。

機組傳動鏈模型中有2個外力矩：1個是氣動輸入力矩；另1個是發電機反饋力矩，當兩者達到平衡時，傳動鏈模型達到穩定運動狀態。

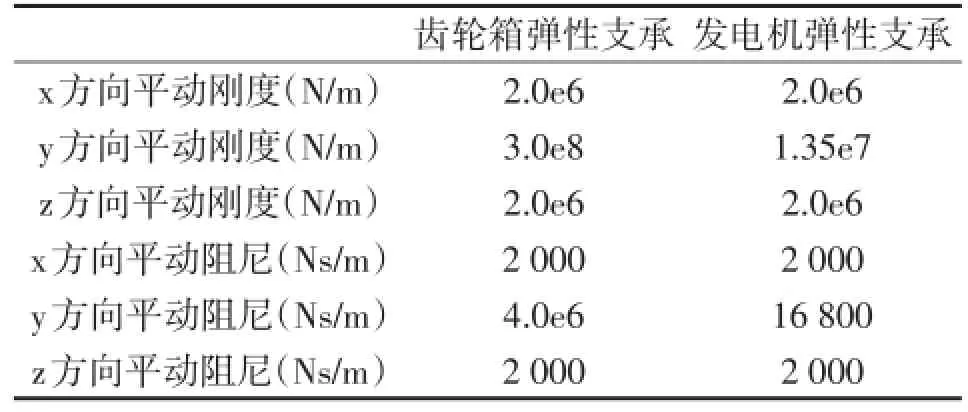
表3　齒輪箱和發電機彈性支承力元參數值

表4　高速軸聯軸器的力元參數值

機組傳動鏈模型仿真分析中，將氣動輸入力矩簡化為作用在輪轂中心的輸入力矩。該力矩通過1個施加在輪轂中心的時間激勵力元表示。根據不同的分析目的，氣動輸入力矩分為傳動鏈動態平衡仿真計算時的輸入力矩和風輪轉速掃頻計算時的輸入力矩。在動平衡計算中，氣動輸入力矩相對于時間是恒定不變的。掃頻計算中，傳動鏈模型將在氣動輸入力矩的驅動下，風輪轉速從切入轉速增加到切出轉速，此時氣動輸入力矩分為2個分量，見式（2）。

式中Tacc為恒定力矩分量，它起到加速傳動鏈轉速的作用；Timb為風輪受風剪和塔影效應引起的不平衡力矩分量。

氣動不平衡力矩分量隨方位角變化情況如圖7所示。

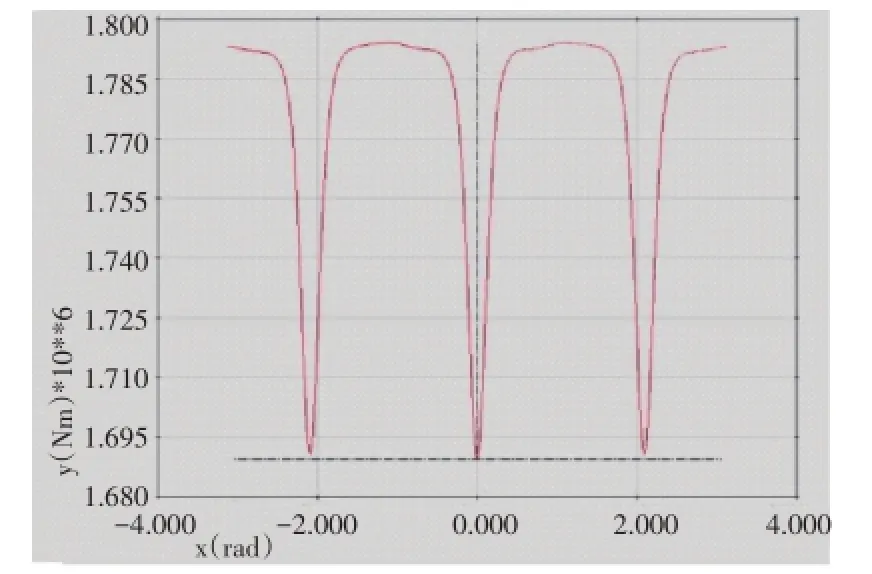
圖7　氣動輸入力矩不平衡分量變化

發電機反饋力矩作用在發電機轉子和定子之間，根據電機輸入轉速給定反饋力矩力元大小。發電機反饋力矩如圖8所示。

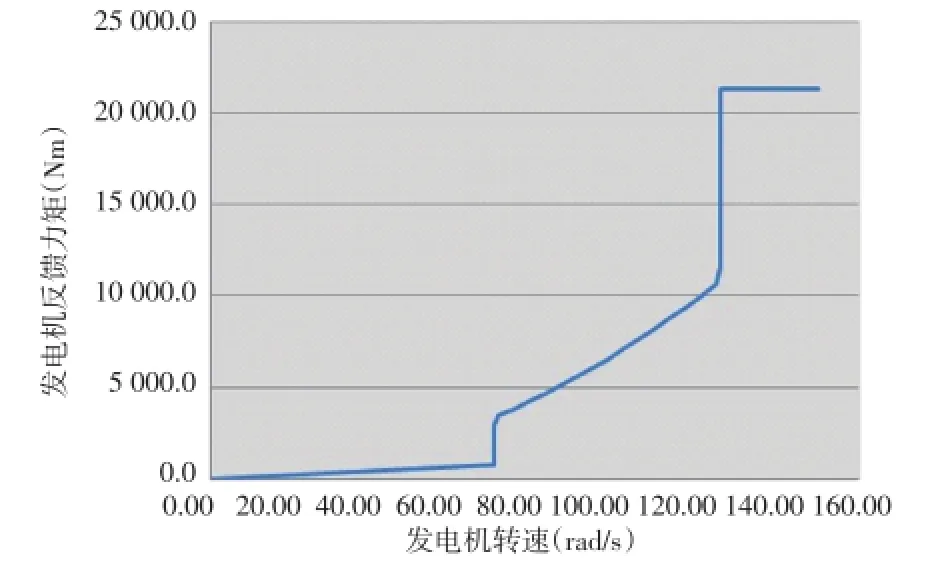
圖8　機組發電機轉速vs力矩曲線

根據2.1節的機組傳動鏈拓撲圖，將以上建立的部件模型根據相互運動關系，用鉸接和力元連接起來，形成某風電機組傳動鏈仿真模型［8］，如圖9所示。

圖9　機組傳動鏈整體模型

3　機組傳動鏈模型頻域分析

根據建立的機組傳動鏈模型，可以對傳動鏈進行頻域分析，包括傳動鏈模態頻率計算、激勵頻率分析、傳動鏈Campbell圖的繪制，以及潛在共振點分析等內容。

傳動鏈模態頻率的計算是在傳動鏈模型上施加恒定氣動輸入力矩及電機反饋力矩，使傳動鏈模型達到穩態運行狀態。然后進行特征值分析，得到傳動鏈模態頻率及模態阻尼因子。由于傳動鏈扭轉方向頻率對動態特性影響較大，因此略去其他方向結果。額定運行點的扭轉模態頻率結果如表5所示。

表5　模態頻率計阻尼因子結果

本文計算了前22階傳動鏈扭轉模態頻率。將分析得到的模態頻率與Bladed計算得到的頻率結果進行比較，如表6所示。

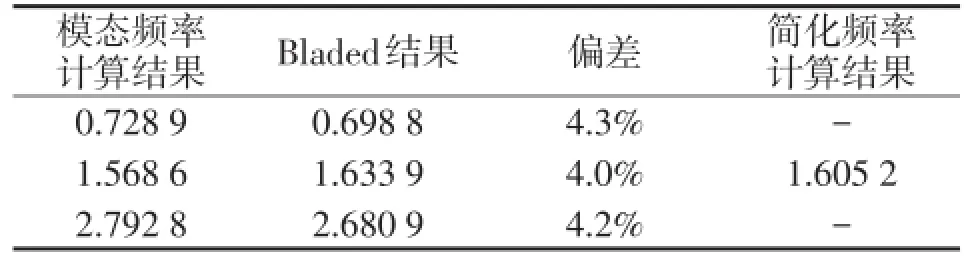
表6　模態頻率結果對比

計算得到的前3階模態頻率與Bladed結果偏差在5%以內，其中1階扭轉模態頻率f_N01為1.568 6 Hz，簡單手算結果為1.605 2 Hz，Bladed計算結果為1.633 9 Hz，計算結果可信。

此外傳動鏈的各階模態頻率在不同工作點處有一定變化。機組在切入、切出工作點下的傳動鏈模態頻率結果如表7所示。

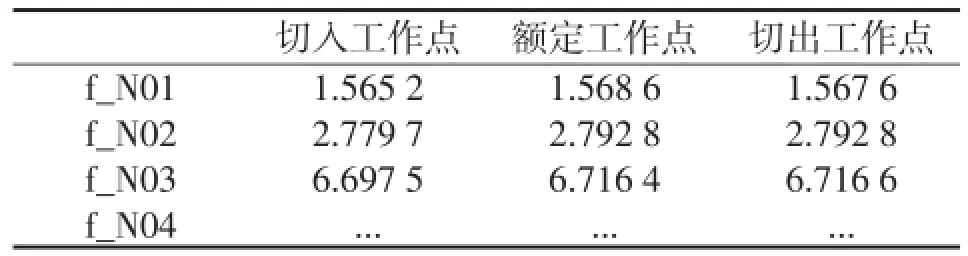
表7　不同工作點下的傳動鏈模態頻率結果

傳動鏈模態頻率在不同工作點處基本完全相同，造成差異的原因是不同工作點下，風輪轉速變化引起的葉片動態剛化現象造成的。

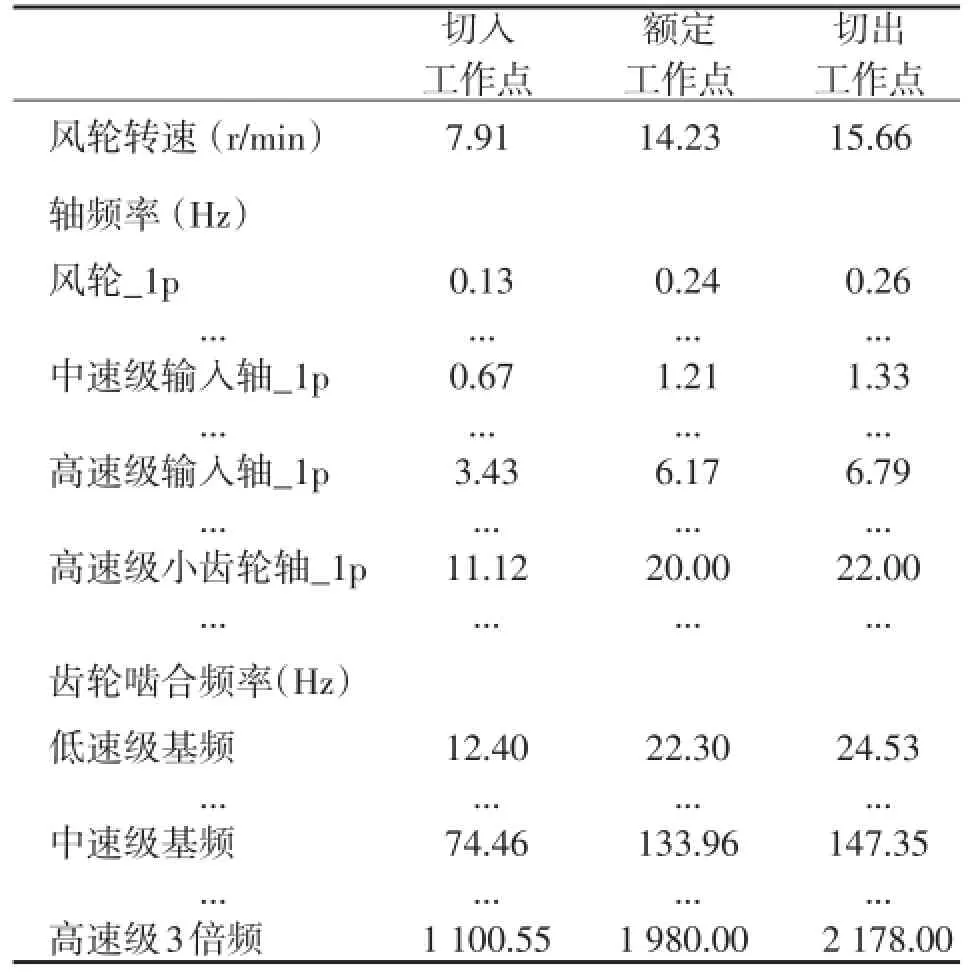
表8　機組傳動鏈激勵頻率

該機組正常運行時，風輪工作轉速在7.91～15.66 r/min之間，額定轉速為14.23 r/min。根據機組運行數據及齒輪箱輪系參數，計算傳動鏈激勵頻率如表8所示。

傳動鏈的最高激勵頻率為高速級齒輪副嚙合頻率的3倍頻：2 178 Hz。由于更高頻率對機組傳動鏈動態特性影響較小，因此在傳動鏈頻率分析中忽略不計。

根據以上計算得到的機組傳動鏈激勵頻率和模態頻率，可以繪制傳動鏈二維Campbell圖。其中模態頻率0～5.6 Hz范圍的Campbell圖如圖10所示。

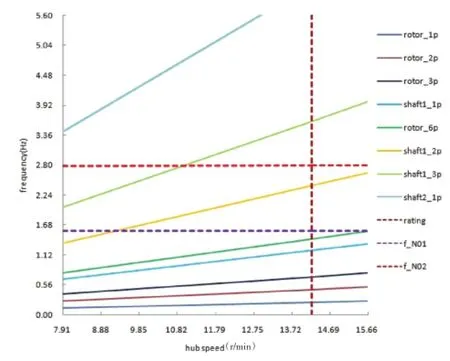
圖10傳動鏈Campbell圖

圖10中縱向坐標為模態頻率，橫向坐標為風輪轉速。水平線表示傳動鏈各階模態頻率，斜線表示傳動鏈激勵頻率，垂直線為風機額定工作點參考線。

Campbell圖中，傳動鏈模態頻率與激勵頻率的交叉點表示機組傳動鏈可能的共振點，但并不意味傳動鏈就會出現共振，這需要結合交點處的部件能量分布和激勵頻率判斷。例如第1階模態頻率與中速級輸入軸2倍頻有交點，其能量分布如圖11所示。

如圖11可見，f_N1的振動能量主要分布在高速軸聯軸器，它與中速級輸入軸激勵頻率shaft1_ 2p有交點。由于產生激勵頻率的部件（中速級）與模態能量集中的部件（聯軸器）不在1個轉速段內，較低的激勵頻率對較高頻率部件的振動激勵影響不明顯，因此認為該交點不會激勵傳動鏈發生共振。相反如果產生激勵頻率的部件與模態能量集中的部件相同，或位于1個轉速段內，那么就有可能產生共振。

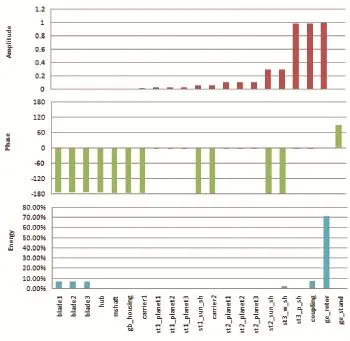
圖11　f_N1的幅值、相位和能量分布情況

Bladed計算得到的一階扭轉頻率的能量如表9所示。

表9　Bladed計算得到的一階扭轉頻率能量表

其中，Generator rotation表示電機轉子的能量百分比；Rotor in plane mode 3表示風輪第3階能量百分比。與圖11比較，主要能量分布在電機轉子和風輪，兩者的部件模態能量分布趨勢一致。

根據以上流程，對傳動鏈Campbell圖中所有交點（共22個交點，這里略去詳細分析過程）逐一進行分析，即可把所有潛在的共振點找出來。但潛在共振點也不一定表示該點會出現傳動鏈共振，需要對潛在共振點進行時域掃頻分析才能最終確定。

4　機組傳動鏈模型時域分析

為了最終驗證機組傳動鏈共振點的個數及位置，需要在時域中對發現的潛在共振點進行掃頻分析。

如2.3節所述，時域掃頻分析時，需要在輪轂中心施加氣動驅動力矩。

傳動鏈模型將從切入轉速加速到切出轉速，如圖12所示。

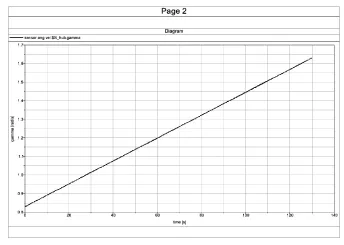
圖12　掃頻分析時輪轂轉速曲線

此時，輪轂角加速度曲線如圖13所示。

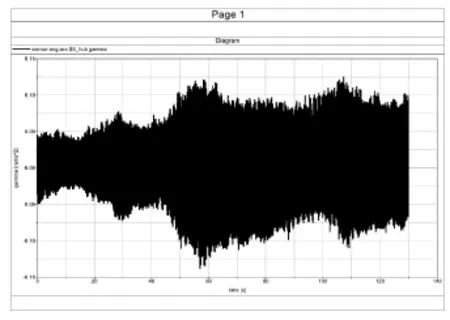
圖13　掃頻分析時輪轂角加速度曲線

在潛在共振點出現的位置，對部件加速度時序數據進行截取和頻譜分析，得到共振點處的部件能量分布。如果該部件能量分布出現明顯的增加或突變，就說明機組傳動鏈在該潛在共振點處出現了共振。

例如，某潛在共振點的機組模態頻率為f_N6= 18.534 5 Hz，激勵頻率為shaft2_3p，模態能量集中在發電機定子。可以求得，f_N6與shaft3_1p的交點處風輪轉速約為13.2 r/min，對應在掃頻分析中的仿真時間點為89.62 s，因此對該時間點附近的發電機定子角加速度時序數據進行頻譜分析，得到的定子角加速度頻譜圖如圖14所示。

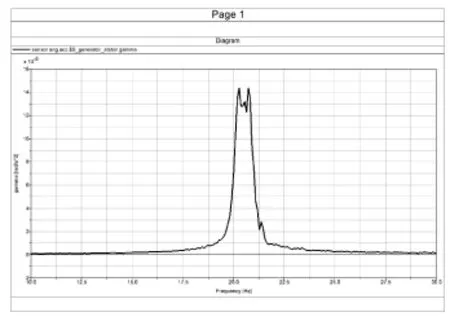
圖14　發電機定子角加速度頻譜圖

如圖14所示，發電機定子角加速度頻譜圖中，在模態頻率f_N6=18.534 5 Hz附近有明顯峰值，但如圖所示，該峰值很小，不超過1.6e-16，說明中速級齒輪軸轉頻的3倍頻對定子振動的激勵可以忽略，因此認為該潛在共振點不會引起共振。

按以上方法對所有潛在共振點進行掃頻分析后，可以得到最終的傳動鏈危險共振點出現的頻率及具體部件。

對于某兆瓦級風電機組傳動鏈，通過頻域及時域動力學分析后，結果顯示該傳動鏈在風電機組運行范圍內沒有共振點，不會引起嚴重共振現象，滿足設計要求。

5　結論

本文以某兆瓦級風電機組傳動鏈為例，繪制了機組傳動鏈動力學拓撲圖，根據德國勞埃德2010版風電機組認證規范的要求，建立了包括具有6個自由度剛柔耦合部件組成的機組傳動鏈模型，該模型具有更多的自由度，仿真結果也更可信。此外，基于建立的機組傳動鏈模型，進行了頻域仿真分析，得到了機組傳動鏈模態頻率、繪制了二維Campbell圖，找到了傳動鏈潛在共振點，并通過時域掃頻分析，驗證了共振點的分析結果。通過與Bladed模型計算結果的對比，顯示仿真分析得到的模態頻率及能量分布的偏差在容許范圍內，驗證了模型和分析結果的正確性。

結果顯示，某兆瓦級風電機組傳動鏈在運行范圍內沒有共振點，不會引起嚴重共振現象，滿足設計要求。

參考文獻

［1］Feike Savenije，Koen Boorsma.Multi Body Simulations at ECN wind［DB］.www.ecn.nl/units/wind.

［2］Berthold Schlecht.State of the art techniques used for determining reliable load assumptions in wind turbine using SIMPACK［DB］.http://www.simpack.com/fileadmin/simpack/ doc/papers/SIMPACK_WIND_2010_IMM_Load_Assumptions.pdf.

［3］Schelenz，T Kamper.Aeroelastic rotors in multi-body simulation［DB］.http://www.simpack.com/fileadmin/simpack/ doc/papers/SIMPACK_WIND_2010_RWTH_AerolasticRotors_n.pdf.

［4］Stefan Hauptmann，Denis Matha，Thomas Hecquet.Aeroelastic load simulations and aerodynamic and structural modeling effects［DB］.

［5］Germanishcher Lloyd.Guideline for the Certification of Wind Turbines［S］.2010:7-34.

［6］機械設計手冊編委會.機械設計手冊:第5卷［M］.北京:機械工業出版社，2004.

［7］ANSYS.ANSYS Workbench 13 Help Documentation.

［8］Simpack.Simpack 8904 Help Documentation.

Research on Dynamics Modeling and Simulation Method of Drive Train for Mega-watts Wind Turbine

Liu Hua，Deng Liang，Yang Xiaolin
（Dongfang Electric Wind Power Co.，Ltd.，Deyang Sichuan，618000）

Abstract:A topology graph of the drive train for mega-watts wind turbine has been drawn and a multi-body dynamic model of the drive train has been built according to GL2010 guideline.Firstly，frequency-domain analysis has been conducted based on the model，the modal frequency of the drive train has been found，and 2D Campbell diagram has been generated to find the potential point of reso?nance.Secondly，the analysis result of resonance point has been verified by sweep analysis in time-domain.The correctness of the sim?ulation result has been verified by comparing with the Bladed result.

Key words:mega-watts wind turbine，drive train，dynamics simulation

中圖分類號：TK83

文獻標識碼：A

文章編號：1674-9987（2016）02-0051-08

DOI:10.13808/j.cnki.issn1674-9987.2016.02.013

作者簡介：劉樺（1975-），男，博士，副主任工程師，2009年畢業于重慶大學機械工程學院機械制造及其自動化專業，現主要從事風機整機及關鍵零部件設計工作。