萬有引力莫非是幾何效應？

趙崢，1967年畢業于中國科技大學物理系，1981年于北京師范大學天文系獲碩士學位，1987年于布魯塞爾自由大學獲博士學位。曾任北京師范大學研究生院副院長、物理系主任、中國引力與相對論天體物理學會理事長、中國物理學會理事。現為北京師范大學物理系教授，理論物理博士生導師、教育學博士生導師。

等效原理揭示引力效應與慣性效應之間確實存在本質聯系。

伽利略的自由落體定律告訴我們，在真空狀態下，引力場中自由下落的各種小球，不管它們的物質組成（例如金球、石球還是木球），也不管它們的質量大小，下落規律都是相同的。推而廣之，設想若干在真空引力場中做斜拋運動的小球，只要它們拋射的角度相同，離開彈射器時的初速也相同，那么不管它們的物質成分和質量大小如何，它們也將描出同樣的軌跡。

我們知道，通常一個物體在外界環境中受到的外力大小，往往與物體的物質成分、物理狀態有關。例如，一個物體在電磁場中受到電磁力的大小，與它是金屬還是非金屬，它是否帶電，帶電多少等有關。而且，不同物體在同一個電磁場中的運動軌跡，不僅和物體的物理成分及狀態有關，也與它們的質量大小有關。但是引力場中的小球運動，居然與這些物理因素都無關，這是怎么回事呢？實在是太神奇了。

愛因斯坦意識到，萬有引力不是一般的力，與我們通常熟悉的所有的力都不同。這是一種極為特殊的力。愛因斯坦反復思考這個問題，突然眼前一亮：萬有引力莫非是一種“幾何力”？莫非真如黎曼的推測，真實的空間可能是彎曲的？萬有引力莫非是時空彎曲導致的幾何效應？

愛因斯坦回憶起，在奧林匹亞科學院的活動中，他們幾個年青人曾一起讀過數學大師龐加萊的科普著作《科學與假設》。在那本書里，他們曾讀到羅巴切夫斯坦和黎曼等發現的非歐幾何，這一幾何描述彎曲的空間。黎曼等數學家曾推測，真實的空間有可能不是平的，而是彎的，而且真實的空間有可能不是三維的，而是四維的，甚至更高維的。該書的內容曾使這幾個年青人一連幾個星期興奮不已。

現在，愛因斯坦看到，黎曼等人的數學結果，竟然與自己當前研究的物理問題有關，這太讓人興奮了。

我們通常學習的幾何，都是歐氏幾何。歐氏幾何產生于人類文明的發源地古埃及和兩河流域，起源于河水泛濫后重新劃分土地的需要，以及建筑等生產活動的需要。在公元前300年左右，在埃及亞歷山大城工作的希臘數學家歐幾里得把積累起來的幾何知識集其大成，寫成一部《幾何原本》。我們中學學習的幾何知識，都來源于此，都沒有超出當年歐幾里得的水平。

歐幾里得幾何以它概念的清楚、知識的豐富、邏輯的嚴密而著稱。《幾何原本》的全部知識建立在幾條公設的基礎上。全書從這幾條公設出發，推出了全部幾何知識。

在驚嘆歐氏幾何的完美的同時，有少數數學家覺得似乎它還有可以改進的地方。例如，一些人注意到它的“第五公設”，即我們通常所說的平行公設：

“過直線外一點，可以引，而且只可以引一條直線，與原直線平行（即不相交）。”

這些人覺得這條公設比其他公設都長，有點遺憾。于是有人試圖從其他公設推導第五公設，如果能夠推出，就可以取消這條公設，此公設的內容就可以當作定理了。這樣，歐氏幾何會顯得更簡潔，更完美。令人意外的是，這件工作十分困難。有關推導第五公設的嘗試進行了1000多年，仍然沒有進展。

到19世紀的時候，情況發生了變化，俄羅斯喀山大學教授羅巴切夫斯基做出了突破。他用反證法假設“過直線外的一點可以引兩條以上的直線與原直線平行”，試圖推出謬誤。然而始終見不到謬誤的影子。這時他的思想產生了一個飛躍：看來也可以用“過直線外的一點可以引兩條以上的平行線”取代第五公設，從而建立起一套新幾何，這套新幾何應該是與歐氏幾何并列的另一套幾何體系。他非常興奮，把有關的研究成果寫成論文，寄給位于首都彼得堡的科學院。但是彼得堡科學院的數學家的思想都跳不出歐氏幾何的束縛，都看不懂羅巴切夫斯基的論文。羅巴切夫斯基只好把自己的研究成果發表在喀山大學學報上。

由于喀山遠離世界數學中心，沒有人能看到羅巴切夫斯基的工作，于是他到歐洲內地宣傳自己的學術觀點。然而還是沒有人肯定他的工作。他在德國作報告時，大數學家高斯參加了會議。年近9旬的高斯聽完報告沒有對他的新幾何發表意見，只是建議德國科學院授予他通訊院士的稱號。這是給予外國學者的最高榮譽，承認他是—位杰出的數學家，但沒有具體對他的新幾何發表看法。事后，高斯在自己的日記中，以及給朋友的信中都提到過羅巴切夫斯基的新幾何。高斯說，他相信當時在會場上，只有他一個人聽懂了羅巴切夫斯基的報告。實際上，高斯早就思考過類似的問題，得到過類似的成果。但是由于歐氏幾何是教會推崇的，高斯膽小，他想到了哥白尼提出日心說的遭遇，于是決定對此保持沉默。

羅巴切夫斯基遺憾地回到家鄉。后來他雙目失明，在學生的幫助下完成了全部新幾何的建立。他所創立的幾何，被稱為羅巴切夫斯基幾何，簡稱羅氏幾何。令他欣慰的是，他在逝世前，知道了自己的新幾何已被數學界所承認。人們終于認識到存在一種不同于歐氏幾何的新幾何，稱其為非歐幾何。

不久之后，德國的黎曼采用另一條新公設取代第五公設，創建了另一種非歐幾何。黎曼的新公設認為：“過直線外的一點，一條平行線也得不出來。”

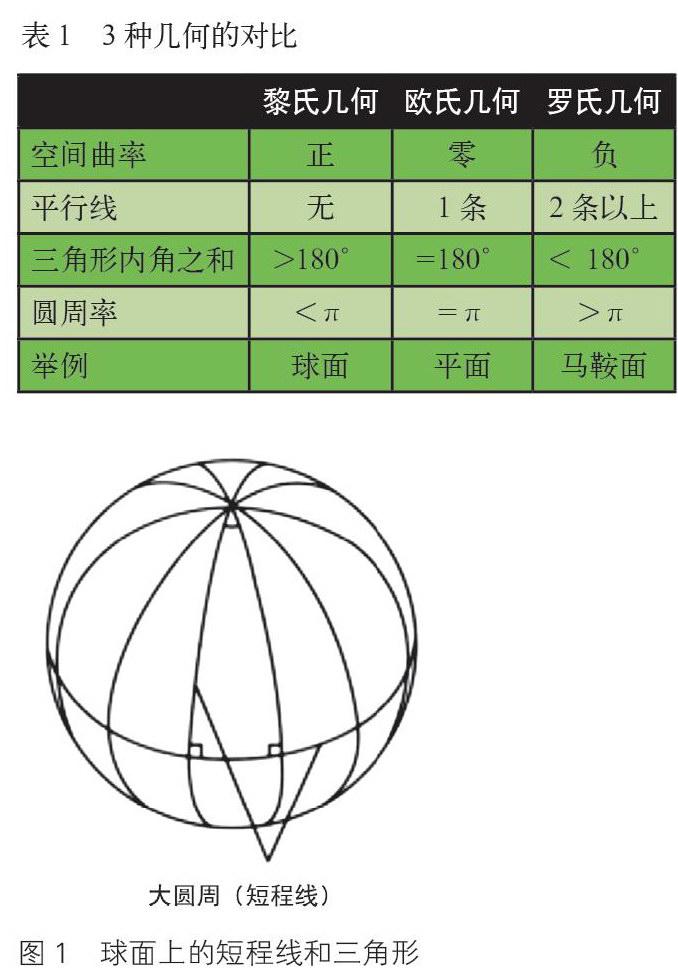
數學界很快認識到這3種幾何都是正確的，它們反映不同曲率空間的性質。人們把羅巴切夫斯基創建的幾何稱為羅氏幾何，把黎曼創建的幾何稱為黎氏幾何。歐氏幾何是平直空間中的幾何，黎氏幾何是正曲率空間中的幾何，羅氏幾何則是負曲率空間中的幾何，這3種幾何的特點列在表1中。

1845年，黎曼把這3種幾何統一起來，統稱為黎曼幾何。他天才地預見到，真實的空間有可能不是平直的，物質的存在有可能造成空間的彎曲。由于當時的物理學還沒發展到應用黎曼幾何的水平，黎曼的預見還僅僅是一種猜測。

前面談到的羅氏空間和黎氏空間都是彎曲空間，彎曲空間中怎么可能會有直線和平行線呢？實際上，彎曲空間中的直線并不是我們通常所說的直線，而是直線在彎曲空間中的推廣。在歐氏幾何中，直線定義為兩點間的最短線。彎曲空間中的兩點之間雖然不可能畫出平常意義下的直線，但兩點之間仍然存在最短線。在黎曼幾何中，把兩點之間的最短線稱為短程線（又稱測地線）。短程線，就是直線在彎曲空間中的推廣。在空間平直的時候，短程線就恢復為我們通常看到的直線。

所謂平行線，就是兩條不相交的直線。所以平行公設在羅氏幾何中表述為：“在一條短程線之外，可以引兩條以上的短程線與其不相交。”在黎氏幾何中則表述為：“在一條短程線之外，不可能引出與其不相交的短程線。”

為了更好地理解黎曼幾何，我們以球面為例加以解釋。球面是正曲率的二維空間，在上面適用的是黎氏幾何。研究表明，球面上的短程線為大圓周。在球面上任取兩點A與B，再加上球心O，這三點可以決定一個平面，此平面與球面的交線就是大圓周。地球上的經線都是大圓周，赤道也是大圓周，但赤道之外的其他緯線都不是大圓周。

從北京飛往多倫多的飛機，從北京起飛后，不像一般人想象的那樣直接向東越過太平洋，而是向東北方向飛，通過中國東北及俄羅斯遠東地區，直奔白令海峽，然后沿阿拉斯加的北海岸飛行，再轉向東南，通過加拿大東部，到達多倫多。有人可能會問，飛機為什么要繞圈子呢，直接往東飛不是近一點嗎？干嘛要繞遠呢？其實，飛機并沒有繞遠，飛機的航線恰好是北京、多倫多和地心這三點決定的大圓周，也就是說，恰好是北京和多倫多之間的短程線。

你可以想一想，能夠過赤道外一點再作一個大圓周與赤道不相交嗎？肯定不行。所以黎氏幾何的平行公設在球面上完全正確。

再看一下球面上的三角形，它由三條短程線圍成。如圖1中，赤道和兩條經線就圍成了一個三角形。容易看出，所有的經線都與赤道垂直，三角形的兩個底角之和已是180°了，再加上頂角，三內角之和肯定大于180°。