層次分析法在鋼材質量控制中的應用

於友?（重慶交通大學 土木工程學院，重慶 400074)

層次分析法在鋼材質量控制中的應用

於友?
（重慶交通大學 土木工程學院，重慶 400074)

本文根據影響鋼材質量的各種因素，運用層次分析法，定量確定出影響鋼材質量各因素的相對重要性。為鋼材質量控制提供一定的理論依據與實踐指導。

鋼材；質量控制；層次分析法

引言

鋼材由于其強度高，質量輕，便于施工等特點，廣泛應用于建筑結構領域，尤其在大跨度結構和高聳結構中[1]。鋼材質量的好壞直接關系到建筑物的安全，以及建筑工程的質量。本文應用層次分析法[2]，對影響鋼材質量的各因素進行分析，定量確定出影響鋼材質量各因素的相對重要性。為鋼材質量控制提供一定的理論依據與實踐指導。

1 層次分析法的原理

層次分析法是一種定性與定量相結合的、系統化、層次化的分析方法。其基本思路是將復雜的問題按照一定的原則分解為若干個組成因素，并將這些因素按支配關系分組形成有序的遞階層次結構。采取兩兩比較的方式確定層次中各因素的相對重要性，構建判斷矩陣。通過對判斷矩陣特征向量與特征值的計算，得出比較因素的權重大小相對值，并進行一致性檢驗。

2 層次分析法應用于鋼材質量控制的基本步驟

2.1 建立層次結構模型

以鋼材質量為目標層，化學成分、冶煉質量和施工質量為準則層。根據影響鋼材質量的各種因素建立鋼材質量的層次結構[3]，如圖1所示。

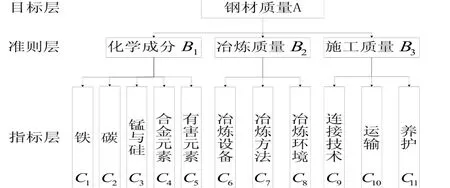
圖1 鋼材質量的層次結構

2.2 構造判斷矩陣

判斷矩陣采取九分制評分法[4]，如表1。根據專家經驗以及兩兩比較建立判斷矩陣，目標層與準則層建立判斷矩陣A B- ，如表2；準則層中化學成分與指標層建立判斷矩陣 1B C- ，如表3，準則層中冶煉質量與指標層建立判斷矩陣，如表4，準則層中施工質量與指標層建立判斷矩陣B3- C，如表5。

表1 1-9尺度的含義說明

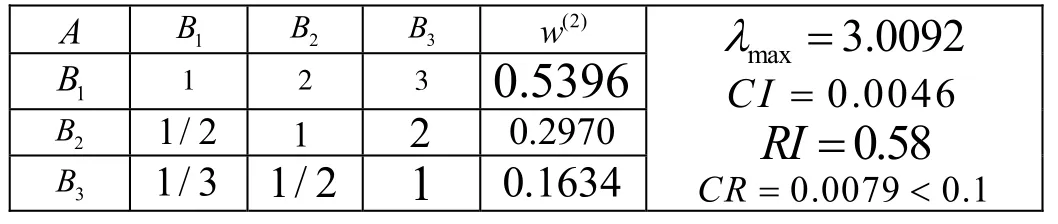
表2 判斷矩陣A B-

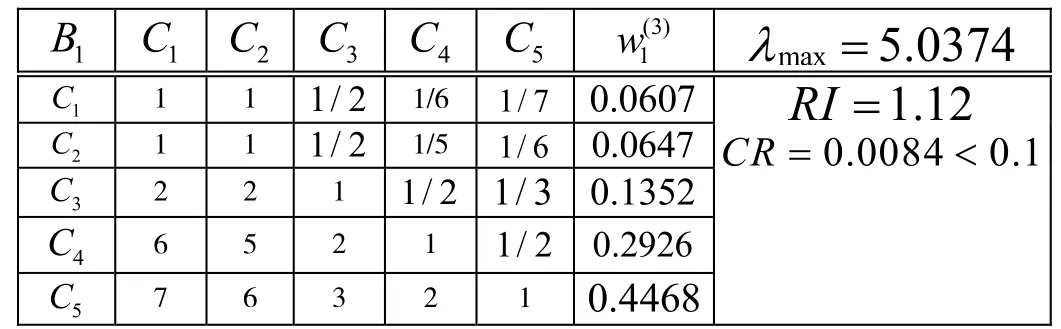
表3 判斷矩陣 1B C-

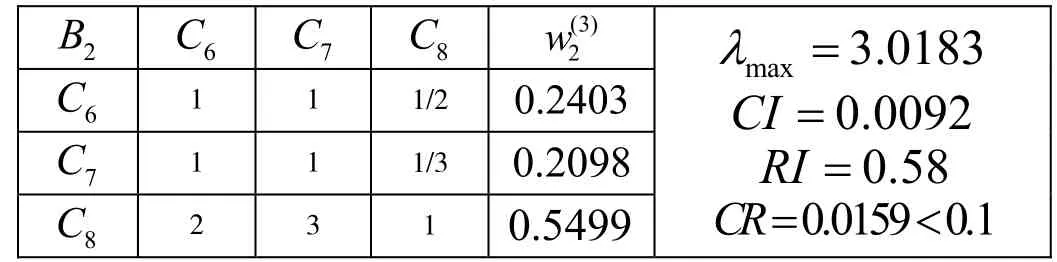
表4 判斷矩陣 2B C-

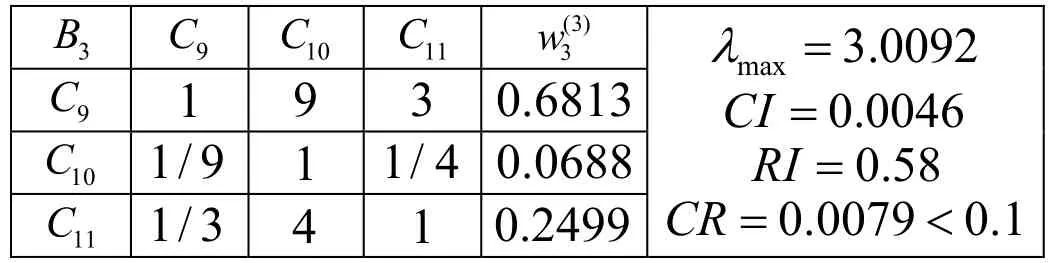
表5 判斷矩陣 3B C-

2.3 權向量的計算與一致性的檢驗

（1）利用MATLAB軟件計算出判斷矩陣的最大特征根 maxλ 以及最大特征根所對應的特征向量[5]，將特征向量歸一化后，得到各元素在單一原則下的權向量w；

（3）確定隨機一致性指標RI,RI的值如表6；

（5）一致性分析，當 0.1 CR＜ 時，判斷矩陣一致性檢驗合格，否則需要重新調整判斷矩陣。

通過上述步驟計算，可以得到判斷矩陣A B- ，判斷矩陣 1B C- ，判斷矩陣 2B C- 和判斷矩陣3B C- 的權向量和一致性檢驗結果，如表2至表5。

表6 隨機一致性指標RI的數值

2.4 組合權向量的計算與組合一致性的檢驗

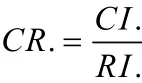
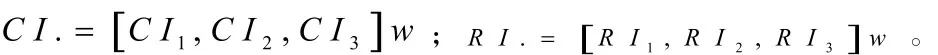
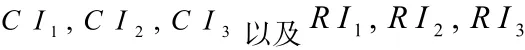
表7 組合權重

3 結語

通過應用層次分析法對影響鋼材質量的各因素進行了分析，確定出鋼材質量控制的重點為控制鋼材中有害元素的含量以及冶煉鋼材的環境。

[1] 李光范.鋼結構[M].哈爾濱:哈爾濱工業大學出版社,2015:2-6.

[2] 姜啟源,謝金星,葉俊.數學模型[M].北京:高等教育出版社,2015:249-256.

[3] 王會波.鋼材性能的影響因素探究[J].產業與科技論壇,2014,(21):116-117.

[4] 許崇山,李國輝.層次分析法在混凝土質量控制中的應用[J].低溫建筑技術,2008,(2):159-160.

[5] 宋飛,趙法鎖.地下工程風險分析的層次分析法及MATLAB應用[J].地球科學與環境學報,2008，(3):292-296.

G322

B

1007-6344（2016）04-0349-02