索網(wǎng)結(jié)構(gòu)中的空間兩節(jié)點懸鏈線索單元

劉玥君，湯愛平，劉克同

(1.東北電力大學 建筑工程學院，吉林 吉林132012； 2.哈爾濱工業(yè)大學 土木工程學院，黑龍江 哈爾濱 150090)

?

索網(wǎng)結(jié)構(gòu)中的空間兩節(jié)點懸鏈線索單元

劉玥君1，湯愛平2，劉克同2

(1.東北電力大學 建筑工程學院，吉林 吉林132012； 2.哈爾濱工業(yè)大學 土木工程學院，黑龍江 哈爾濱 150090)

摘要：為了分析索結(jié)構(gòu)在荷載作用下的線性和非線性反應(yīng)，根據(jù)索結(jié)構(gòu)的受力特點，提出了一種可以充分考慮索結(jié)構(gòu)非線性效應(yīng)的空間兩節(jié)點懸鏈線索單元。基于彈性懸鏈線的解析解，推導了索單元的切線剛度矩陣,通過迭代法求解了索結(jié)構(gòu)的剛度矩陣和內(nèi)力向量，利用該新型的索單元模型分析了靜、動力荷載作用下結(jié)構(gòu)的非線性行為,對于非線性靜力分析，結(jié)構(gòu)平衡方程采用牛頓迭代法求解；對于非線性動力時程分析，采用Newmark直接積分法和牛頓迭代法相結(jié)合的增量迭代法求解。數(shù)值分析結(jié)果驗證了空間兩節(jié)點懸鏈線索單元模擬索結(jié)構(gòu)的精確性和可靠性。

關(guān)鍵詞：空間兩節(jié)點；懸鏈線索單元；靜力荷載；動力荷載；非線性分析

網(wǎng)絡(luò)出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160421.1040.030.html

近幾十年來，索結(jié)構(gòu)廣泛的應(yīng)用于輸電線、斜拉橋等大跨越空間結(jié)構(gòu)。索結(jié)構(gòu)具有很強的非線性特性，索結(jié)構(gòu)受力分析需要考慮擾度和大變形的影響。在索結(jié)構(gòu)的研究方面，陳太聰?shù)萚1]總結(jié)和分析了不同工況下索結(jié)構(gòu)中拉索的受力特點，將拉索行為歸納為已知原長和已知索力兩種典型受力情況。利用懸鏈線拉索解析解的線性展開，引入適當?shù)募s束條件，建立兩種新型的拉索單元，提出索結(jié)構(gòu)非線性靜力分析的一般迭代算法，利用等效線自重考慮彈性變形對拉索靜力狀態(tài)的影響。魏建東等[2]基于有限元分析的基本原理，創(chuàng)建了一種新的滑移索單元，分析索結(jié)構(gòu)中索段在鞍座上的滑動問題。唐建民等[3]根據(jù)張拉結(jié)構(gòu)的特點，提出了一種五節(jié)點等參數(shù)單元有限元模型，采用四節(jié)點多項式作為位移差值函數(shù)及單元初始形狀函數(shù)，基于修正的Lagrangian坐標描述法，建立了非線性有限元基本方程和切線剛度矩陣，利用Newton-Raphson法進行了實例計算。黃濤等[4]提出了具有扭轉(zhuǎn)自由度的五節(jié)點索單元非線性有限元法，考慮了索結(jié)構(gòu)沿軸向的轉(zhuǎn)動自由度，這種方法不僅適用于一般的懸索結(jié)構(gòu)的分析，也適用于需要考慮扭轉(zhuǎn)的特殊懸索結(jié)構(gòu)的分析。

現(xiàn)有的索結(jié)構(gòu)數(shù)值分析技術(shù)主要采用下面兩種方法:1)基于多項式插值函數(shù)的有限元方法，2)基于彈性懸鏈線解析表達式的分析方法。在第1種方法中，采用插值函數(shù)來描述索結(jié)構(gòu)的非線性，這種方法常用來模擬兩節(jié)點和多節(jié)點單元及具有轉(zhuǎn)動自由度的曲線單元，但是該方法只適合模擬具有較大預應(yīng)力的索結(jié)構(gòu)。對于長度較小，承受拉力較高的索，采用等效彈性模量來計算是足夠準確的，但對于弧垂比較大的索，該方法的適用性較差[5]。對大弧垂索結(jié)構(gòu)，一般采用一系列的直線單元來模擬幾何彎曲的索結(jié)構(gòu)，多節(jié)點索單元是基于高階多項式的插值函數(shù)[6-8]來構(gòu)造，因此計算結(jié)果的精度較兩節(jié)點索單元有一定的提高，但多節(jié)點單元會破壞索結(jié)構(gòu)曲線斜率的連續(xù)性。除此之外，多節(jié)點單元需要使用大量的單元來建立幾何彎曲的索結(jié)構(gòu)模型，對于多索結(jié)構(gòu)體系，這種方法的計算成本巨大。第二種方法是由Jayaraman 等[9]提出的采用彈性懸鏈線的精確表達式來描述索結(jié)構(gòu)的真實力學行為，經(jīng)過Wang[10]、 Andreu[11]、 Yang[12]、Such[13]、Andreu[14]等進行改進。用懸鏈線單元對曲線索結(jié)構(gòu)進行建模，與多項式插值函數(shù)有限元方法相比有很多優(yōu)點，如計算需要的自由度數(shù)少，可以完全考慮索結(jié)構(gòu)的非線性效應(yīng)。

基于彈性懸鏈線解析理論，本文開發(fā)了一種空間兩節(jié)點懸鏈線索單元，用來對索結(jié)構(gòu)承受的靜態(tài)和動態(tài)荷載進行非線性分析。考慮索結(jié)構(gòu)的預應(yīng)力效應(yīng)，推導并給出索單元的切線剛度矩陣和內(nèi)部力向量。采用構(gòu)造的索單元對弧垂較小的索網(wǎng)結(jié)構(gòu)和弧垂較大的輸電線索結(jié)構(gòu)進行計算分析，并對計算結(jié)果進行了驗證。

1懸鏈線索單元

為了能夠模擬索結(jié)構(gòu)的真實形態(tài)，根據(jù)彈性懸鏈線單元的解析表達式，本文推導出來一種新的懸鏈線索單元。假設(shè)索結(jié)構(gòu)是完全柔性的，自重沿索長度均勻分布，索的橫截面積保持不變。圖1顯示

了索結(jié)構(gòu)兩懸掛點I、J的笛卡爾坐標分別為(0，0，0)和(lx，ly，lz)，s和p為變形前后索上任意一點的曲線坐標。索在平衡時的方程可以表示為

(1)式中：F1、F2和F3分別是索結(jié)構(gòu)在x、y和z軸的張力分量，w是索結(jié)構(gòu)的自重，索結(jié)構(gòu)的張力在拉格朗日坐標下的表達式為

(3)式中：E是索的彈性模量，A是索的橫截面積。曲線坐標s與笛卡爾坐標之間的關(guān)系可以表示為

(4)

圖1　三維懸鏈線索單元Fig.1　Three-dimensional catenary cable element

(5)將方程(1)～(3)代入方程(4)，引入邊界條件(5)，索的長度在x、y和z 3個方向的分量為

(6)

式中：L0是索的原長，根據(jù)端部節(jié)點力(F1，F(xiàn)2，F(xiàn)3)，lx、ly和lz可以表示成如下形式：

(7)

切線剛度矩陣和相應(yīng)單元的內(nèi)力向量可以通過求解方程(6)來推導，對方程(6)的兩邊同時進行微分，可以得到下面的方程：

(8)

或表示成矩陣的形式：

(9)

F是柔度矩陣，具體可以表示為

(10)

式中：Ti和Tj分別是節(jié)點I、J的張力，可以定義為

(11)

節(jié)點J的節(jié)點力(F4，F(xiàn)5，F(xiàn)6)可以通過平衡方程獲得

(12)

剛度矩陣通過對求柔度矩陣F的逆矩陣而得到

(13)

索單元的切線剛度矩陣和內(nèi)力向量可以表示成六自由度的形式：

(14)

(15)

如果索單元的切線剛度矩陣和內(nèi)力向量已經(jīng)確定，索長和索的弧垂如圖2可以獲得[9,14]：

(16)

(17)

式中：

(18)

圖2　斜拉索的弧垂ZsFig.2　The sag of stay cable Zs

采用彈塑性鉸模型來表示索單元的非彈性行為，假設(shè)索單元的塑性分布是集中在索的兩端，而整個索單元仍然保持彈性。如果索的軸向力大于屈服力Py=Aσy，索單元的彈性模量等于零，軸向力等于屈服力Py[15]。

2剛度矩陣及求解方法

應(yīng)用迭代算法來計算索單元的切線剛度矩陣和內(nèi)力向量。這個程序的計算需要端點力的初值(F1，F(xiàn)2，F(xiàn)3)，根據(jù)已知的懸鏈線方程，端點力的初值可以通過以下的方式獲得[9]

(19)

式中：

(20)

計算切線剛度矩陣和內(nèi)力矢量的迭代程序如下：

1)輸入w、E、A、L0，節(jié)點I(xi,yi,zi)和節(jié)點J(xj,yj,zj)。

2)計算lx0=xj-xi，ly0=yj-yi，lz0=zj-zi。

4)使用式(6)更新(lx，ly，lz)。

5)計算閉合差向量

6)如果dL小于預設(shè)的允許值，應(yīng)用式(14)計算KT，用式(15)計算Fint，如果dL大于預設(shè)的允許值，程序繼續(xù)進行下一步。

7)計算端點力的修正向量dF=F-1dL。

8)更新端點力Fi+1=Fi+dF，然后回到4)。

如果給定索單元的張力初值為T0，索原長未知，可以采用一個類似的迭代程序來計算無應(yīng)力索的原長，具體迭代程序如下：

1)輸入w，E，A，節(jié)點I(xi，yi，zi)和節(jié)點J(xi，yi，zi)。

2)計算lx0=xj-xi，ly0=yj-yi，lz0=zj-zi。

3)對索原長L0和端點力(F1，F(xiàn)2，F(xiàn)3)進行初始化：

(21)

4)使用式(6)更新(lx，ly，lz)。

5)計算閉合差向量

6)如果dL小于給定的允許值，現(xiàn)有的L0是索原長。如果dL大于預設(shè)的允許值，程序繼續(xù)進行下一步。

7)將式(6)分別對F2，F(xiàn)3和L0進行微分，得到矩陣D。

(22)

9)更新F2=F2+dF2,F3=F3+dF3,L0=L0+dL0，然后回到4)。

對于非線性靜力分析，每一個荷載增量的殘余力使用牛頓迭代法進行離散，對于非線性時程分析，采用增量迭代法，以Newmark直接積分法和牛頓迭代法為基礎(chǔ)，來求解非線性運動方程。結(jié)構(gòu)的增量運動方程可以寫成如下的形式：

(23)

(24)

式中：αM和αK分別是質(zhì)量和剛度比例阻尼系數(shù)，采用將Newmark法中常平均加速度法(γ=1/2,β=1/4)，增量加速度和速度在每一時間步的第一次迭代可以寫成：

(25)

(26)

式中：n為迭代次數(shù)，將方程(25)和(26)代入到方程(23)中，增量位移可表示為

(27)

(28)

(29)

在每一時間步的第一次迭代，基于增量位移向量Δu，對時間t+Δt時的總位移，速度和加速度進行更新。

(30)

(31)

(32)

對于每個時間步的第二次以及后續(xù)的迭代，可以求解結(jié)構(gòu)體系在殘余力ΔR作用下的解。

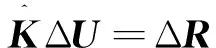
(33)

根據(jù)總外力F、慣性力、阻尼力和更新的內(nèi)力Fint計算殘余力ΔR為

(34)

一旦計算滿足收斂準則，結(jié)構(gòu)響應(yīng)在下一步被更新為

(35)

(36)

(37)

(38)

3數(shù)值驗證

3.1索網(wǎng)結(jié)構(gòu)

此算例來自文獻[4]。該問題不考慮轉(zhuǎn)動自由度，只需將外力矩設(shè)為零即可。圖3為索網(wǎng)的離散圖，圖4為索網(wǎng)的初始幾何形狀。每根索的截面面積為1.48 cm2，彈性模量為82.68 GPa，標號為3、4、8和11的水平位置的四根索的預應(yīng)力為37.61 MPa，其余傾斜的索的預應(yīng)力為36.69 MPa。采用12個兩節(jié)點非線性空間索單元劃分此索網(wǎng)，豎直集中載荷同時作用在4、5、8和9 4個連接點上，大小為都為55.12 MPa，計算時取相對誤差限為0.01，為簡潔起見，表1只給出了典型連接點4的位移分量，同時給出了文獻[4]采用五節(jié)點索單元的計算結(jié)果。

圖3　索網(wǎng)離散圖Fig.3　The discrete figure of cable-nets

圖4　索網(wǎng)初始幾何形狀Fig.4　The initial geometry of cable-nets

分量本文結(jié)果文獻[4]結(jié)果X-1.4642-1.4644Y-0.1318-0.1318Z0.13160.1318

從表1可以看出，采用空間兩節(jié)點懸鏈線索單元與采用五節(jié)點索單元計算的結(jié)果非常接近，說明應(yīng)用空間兩節(jié)點懸鏈線索單元來模擬索網(wǎng)結(jié)構(gòu)的方法和程序是正確可靠的。

3.2輸電線動力響應(yīng)分析算例

3.2.1算例1

索結(jié)構(gòu)在風荷載作用下表現(xiàn)出很強非線性特性[3,16]，采用本文提出的兩節(jié)點非線性空間索單元計算索結(jié)構(gòu)的非線性時程反應(yīng)。為驗證該方法的正確性，同時應(yīng)用ANSYS有限元分析軟件進行計算，選取在實際工程中使用的500 kV貓頭塔，該輸電塔總高為56.2 m，呼稱高為42 m，跨距為300 m。利用空間梁單元模擬塔的桿件，將導線看成理想的柔性索，用桿單元來模擬導線，建立輸電塔-線耦合的空間有限元模型，塔底和線端處理成固結(jié)。塔的材料阻尼比取0.03，如圖5所示。導線選用4×LGJ-400/35型鋼芯鋁絞線，將四分裂導線簡化為一根導線建模，根據(jù)GB/T 1179-2008《圓線同心絞架空導線》[17]查得技術(shù)參數(shù)如表2所示。

圖5　輸電塔-線耦合的空間有限元模型Fig.5　The coupled transmission tower-line system

導線根數(shù)橫截面積/mm2計算抗拉斷力/N單位長度質(zhì)量/(kg·km-1)直徑/mm單根425.24103900134923.27四根1700.96415600539646.55

本文采用AR法[18]同時模擬了78點的空間脈動風速，但由于輸電塔屬于高聳結(jié)構(gòu)，所以縱向脈動風速譜選用沿高度變化的Kaimal譜，自然風場對結(jié)構(gòu)離散化節(jié)點的脈動作用在空間上存在位置相干性，當輸電線路位于陡坡地段或桿塔不等高時，導線落差梯度較大，或由于導線跨距較大，導線垂度效應(yīng)明顯時，各離散點的平均風速和風速譜均不相同，應(yīng)同時考慮了橫向與豎向的空間相關(guān)性。

(39)

式中：SV是功率譜密度，f是頻率，V*是剪切速度，f*為無量綱的Monin坐標。不同高度處的風速作用的相位是不同，一般先作用于結(jié)構(gòu)的較高處，然后到達較低的結(jié)構(gòu)，作用時差為f, 可以用互功率譜密度函數(shù)來表達這些信息，互譜函數(shù)一般為復數(shù)形式：

(40)

圖6　風速時程Fig.6　Wind velocity time-history

圖7　脈動風速功率譜密度Fig.7　The power spectral density of wind velocity

假設(shè)模型所處位置標準高度(10 m) 處的平均風速為V10= 10 m/s, 地面粗糙度系數(shù)k=0.005；脈動風速時間間隔為0.05 s，共模擬了600 s的風速數(shù)據(jù),風速時程曲線如圖6所示，圖7為脈動風速功率譜密度，可以看出模擬譜與目標譜吻合較好，可以用于本文中的時程分析。經(jīng)過分析，得出了子導線1中點的位移時程曲線，如圖8，圖中實線給出了由本文方法得到的子導線1中點位移時程曲線。虛線為有限元分析軟件ANSYS的計算結(jié)果，從兩條曲線的分布情況可以看

出,本文方法和ANSYS計算得到的子導線1中點處的豎向位移、橫向位移結(jié)果基本一致，但是在計算時間上，采用ANSYS計算在4 248 s時達到收斂，采用本文方法的計算達到收斂時間為700 s, 因此，應(yīng)該空間兩節(jié)點索單元進行計算，在滿足計算的正確性和精度的同時，可以節(jié)省計算時間，降低計算代價。

3.2.2算例2

文獻[19]中采用三節(jié)點曲線梁法分析單跨輸電線路，導線為單導線，輸電線路主要是由輸電塔、輸電線、絕緣子、間隔棒以及其他連接金具構(gòu)成，對于一個輸電線路的截斷模型，輸電塔、絕緣子串和相鄰跨的剛度可以用簡化的彈簧模型來表示，如圖9(a)所示。Kx、Ky、Kz分別表示輸電線兩端輸電塔、絕緣子以及相鄰子跨在x、y、z方向上的簡化邊界條件。導線選用LGJ-400/50型鋼芯鋁絞線，檔距為250 m，弧垂為1.3 m，跨中單元的張力為106.8 kN，通過懸鏈線理論對導線進行找形分析。由于覆冰的作用，導線覆冰形狀為新月形，如圖9(b)是覆冰輸電導線的斷面圖，導線直徑為27.6 mm，覆冰厚度為20 mm。導線的軸向剛度為EA=31.1×106N，扭轉(zhuǎn)剛度為GJ=159 Nm2/rad，抗彎剛度為1 965 Nm2，導線的彈性模量為69 000 N/mm2，覆冰導線參數(shù)見表3，新月形覆冰導線的氣動力系數(shù)曲線由風洞試驗測得，分別測試了10 m/s風速下，風攻角在-180°～180°范圍內(nèi)的升力系數(shù)、阻力系數(shù)和扭矩系數(shù)，如圖10。

圖8　風荷載作用下子導線1中點位移變化曲線Fig.8　The displacement at midpoint of subconductor 1 under wind loads

參數(shù)數(shù)值覆冰厚度/mm20裸導線橫截面積/mm2598.28覆冰面積/mm2343.04裸導線單位長度質(zhì)量/(kg·m-1)1.51覆冰導線單位長度質(zhì)量/(kg·m-1)0.308覆冰導線的偏心距/mm19.17

在10 m/s風速，風攻角為-10°情況下，選取時間步長為0.001 s，總的仿真時間為700 s，經(jīng)過計算，得出導線動力響應(yīng)位移時程，截取680～690 s的子導線1中點的位移時程曲線如圖11所示。

圖11　跨中節(jié)點的位移時程曲線Fig.11　The time-history curve of displacement at mid-span node

圖11中實線給出了文獻[19]中采用三節(jié)點曲線梁法來模擬的索單元得到的子導線1中點橫向位移、豎向位移時程曲線。虛線為借助本文方法得出的結(jié)果，從兩條曲線的分布情況可以看出，用本文方法和三節(jié)點曲線梁法計算得到的跨中節(jié)點處的橫向位移、豎向位移的結(jié)果達到非常好的吻合，較好的驗證本文方法及程序的正確性，充分考慮了導線的非線性效應(yīng)，計算中需要的自由度數(shù)更少，有利于節(jié)省計算時間。

4結(jié)論

針對現(xiàn)有索結(jié)構(gòu)模型在模擬非線性方面的不足，本文基于彈性懸鏈線解析理論開發(fā)了一種空間兩節(jié)點懸鏈線索單元。經(jīng)過計算，得出的結(jié)論主要有以下幾點：

1)采用構(gòu)造的空間兩節(jié)點懸鏈線索單元編制計算機程序?qū)〈馆^小的索網(wǎng)結(jié)構(gòu)和弧垂較大的輸電線索結(jié)構(gòu)進行計算分析。可以精確有效的計算懸索結(jié)構(gòu)受到的靜態(tài)和動態(tài)荷載，并給出了相應(yīng)的切線剛度矩陣和內(nèi)力矢量，索網(wǎng)中的每個索單元可以通過一個單元來建模，通過與現(xiàn)有研究結(jié)果比較發(fā)現(xiàn)，本文提出的兩節(jié)點懸鏈線索單元可以很好地預測懸索結(jié)構(gòu)的線性和非線性行為。數(shù)值算例分析驗證了本文方法的有效性和計算程序的準確性。

2)采用兩節(jié)點索單元進行索結(jié)構(gòu)計算無需太多的結(jié)構(gòu)單元及自由度數(shù)即可得到精度較高的計算結(jié)果，對節(jié)省計算時間降低計算代價有利。編制的計算機程序具有良好的通用性，不僅適用于輸電線路這類弧垂較大的索結(jié)構(gòu)的分析，也可以用于大跨度的懸索和索網(wǎng)結(jié)構(gòu)的分析。

參考文獻：

[1]陳太聰, 蘇成, 馬海濤. 索結(jié)構(gòu)靜力分析的新型拉索單元研究[J]. 工程力學, 2014, 31(2): 46-52.CHEN Taicong, SU Cheng, MA Haitao. Study on the development of new-type cable elements for static analysis of cable structures[J]. Engineering mechanics, 2014, 31(2): 46-52.

[2]魏建東. 索結(jié)構(gòu)分析的滑移索單元法[J]. 工程力學, 2004, 21(6): 172-176, 210.

WEI Jiandong. Sliding cable element for the analysis of cable structures[J]. Engineering mechanics, 2004, 21(6): 172-176, 210.

[3]唐建民, 董明, 錢若軍. 張拉結(jié)構(gòu)非線性分析的五節(jié)點等參單元[J]. 計算力學學報, 1997, 14(1): 108-113.

TANG Jianmin, DONG Ming, QIAN Ruojun. A finite element method with five-node isoparametric element for nonlinear analysis of tension structures[J]. Chinese journal of computational mechanics, 1997, 14(1): 108-113.

[4]黃濤, 周金枝, 朱若燕. 具有扭轉(zhuǎn)自由度的五節(jié)點索單元非線性有限元法[J]. 武漢理工大學學報:交通科學與工程版, 2010, 34(6): 1150-1153, 1158.

HUANG Tao, ZHOU Jinzhi, ZHU Ruoyan. A finite element method with five-node cable element with a axial rotational freedom[J]. Journal of Wuhan university of technology:transportation science & engineering, 2010, 34(6): 1150-1153, 1158.

[5]LIEW J Y R, PUNNIYAKOTTY N M, SHANMUGAM N E. Limit-state analysis and design of cable-tensioned structures[J]. International journal of space structures, 2001, 16(2): 95-110.

[6]GRECO L, IMPOLLONIA N, CUOMO M. A procedure for the static analysis of cable structures following elastic catenary theory[J]. International Journal of Solids and Structures, 2014, 51(7/8): 1521-1533.

[7]ABAD M S A, SHOOSHTARI A, ESMAEILI V, et al. Nonlinear analysis of cable structures under general loadings[J]. Finite elements in analysis and design, 2013, 73: 11-19.

[8]CHEN Z H, WU Y J, YIN Y, et al. Formulation and application of multi-node sliding cable element for the analysis of Suspen-Dome structures[J]. Finite elements in analysis and design, 2010, 46(9): 743-750.

[9]JAYARAMAN H B, KNUDSON W C. A curved element for the analysis of cable structures[J]. Computers & structures, 1981, 14(3/4): 325-333.

[10]WANG Chunjiang, WANG Renpeng, DONG Shilin, et al. A new catenary cable element[J]. International journal of space structures, 2003, 18(4): 269-275.

[11]ANDREU A, GIL L, ROCA P. A new deformable catenary element for the analysis of cable net structures[J]. Computers & structures, 2006, 84(29/30): 1882-1890.

[12]YANG Y B, TSAY J Y. Geometric nonlinear analysis of cable structures with a two-node cable element by generalized displacement control method[J]. International journal of structural stability and dynamics, 2007, 7(4): 571-588.

[13]SUCH M, JIMENEZ-OCTAVIO J R, CARNICERO A, et al. An approach based on the catenary equation to deal with static analysis of three dimensional cable structures[J]. Engineering structures, 2009, 31(9): 2162-2170.

[14]THAI H T, KIM S E. Nonlinear static and dynamic analysis of cable structures[J]. Finite elements in analysis and design, 2011, 47(3): 237-246.

[15]劉克同, 湯愛平, 劉玥君, 等. 基于MRT-LBM大渦模擬的橋梁氣動參數(shù)數(shù)值仿真[J]. 四川大學學報:工程科學版, 2013, 45(6): 87-95.

LIU Ketong, TANG Aiping, LIU Yuejun, et al. Numerical simulation for aerodynamic parameters of bridge decks using MRT-LBM-LES[J]. Journal of Sichuan university:engineering science edition, 2013, 45(6): 87-95.

[16]全國電線電纜標準化委員會. GB/T 1179-2008圓線同心絞架空導線[S]. 北京: 中國標準出版社, 2009: 15-17.

[17]OWEN J S, ECCLES B J, CHOO B S, et al. The application of auto-regressive time series modelling for the time-frequency analysis of civil engineering structures[J]. Engineering structures, 2001, 23(5): 521-536.

[18]YAN Zhitao, LI Zhengliang, SAVORY E, et al. Galloping of a single iced conductor based on curved-beam theory[J]. Journal of wind engineering and industrial aerodynamics, 2013, 123: 77-87.

本文引用格式：

劉玥君，湯愛平，劉克同. 索網(wǎng)結(jié)構(gòu)中的空間兩節(jié)點懸鏈線索單元[J]. 哈爾濱工程大學學報， 2016, 37(6): 788-795.

LIU Yuejun, TANG Aiping, LIU Ketong. Spatial two-node catenary element for analyzing cable-net structures[J]. Journal of Harbin Engineering University, 2016, 37(6): 788-795.

收稿日期：2015-03-27.

基金項目：國家國際科技合作專項項目(2011DFA21460).

作者簡介：劉玥君(1983-)，女，講師； 通信作者：劉玥君，E-mail: liuyuejun0221@163.com.

DOI:10.11990/jheu.201503081

中圖分類號：O242.2

文獻標志碼：A

文章編號：1006-7043(2016)06-0788-08

Spatial two-node catenary element for analyzing cable-net structures

LIU Yuejun1, TANG Aiping2, LIU Ketong2

(1.School of Civil and Architecture Engineering, Northeast Dianli University, Jilin 132012, China; 2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China)

Abstract：To analyze the linear and nonlinear behaviors of cable-net structures based on their mechanical characteristics, this paper presents a spatial two-node catenary cable element model (STCCE), which can be used to analyze the nonlinear effect cable structures under static and dynamic loads. The tangent stiffness matrix was derived based on the analytical solutions of elastic catenary; the stiffness matrix and internal force vector were calculated using an iterative algorithm; the nonlinear behavior was analyzed using the new model STCCE under static and dynamic loading. The Newton-Raphson method was applied to sove the structural balance equation for the nonlinear static analysis. An incremental iterative method, based on the Newmark direct integration and Newton-Raphson methods, was used for nonlinear dynamic time-history analysis. The accuracy and reliability of the STCCE were verified using numerical analysis.

Keywords：spatial two-node element； catenary cable element；static load； dynamic load；nonlinear analysis

網(wǎng)絡(luò)出版日期：2016-04-21.

湯愛平(1968-)， 男，教授，博士生導師.