極限彈性性能的材料微結構拓撲優化設計

張　嚴　杜義賢，2　杜大翔　田啟華

(1. 三峽大學 機械與動力學院， 湖北 宜昌　443002； 2. 水電機械設備設計與維護湖北省重點實驗室， 湖北 宜昌　443002)

?

極限彈性性能的材料微結構拓撲優化設計

張嚴1杜義賢1，2杜大翔1田啟華1

(1. 三峽大學 機械與動力學院， 湖北 宜昌443002； 2. 水電機械設備設計與維護湖北省重點實驗室， 湖北 宜昌443002)

摘要：基于應變能等效的能量法，求解材料微結構的等效彈性系數矩陣，以等效彈性系數矩陣主對角線上元素的某項或某幾項的加權組合最大為目標，以材料體積率為約束，構建具有極限彈性性能材料微結構的拓撲優化模型，采用SIMP插值結合優化準則法求解該優化模型，推導了優化求解過程中的敏度表達式，實現了具有極限彈性性能的材料微結構拓撲構型設計．數值算例驗證拓撲優化模型和算法的有效性．

關鍵詞：能量法；材料微結構；極限彈性性能；拓撲優化；SIMP插值

高科技的發展對材料性能提出了越來越高的要求，如零或負的膨脹系數、極端熱傳導系數、負泊松比等特殊的性能．材料的宏觀性能依賴于材料微觀結構的性能，而材料微觀結構的性能取決于微觀結構的尺度、構型及材料組份比，因此，對具有特殊宏觀性能的材料可以通過對其微觀結構的設計來實現[1]．國外學者如Sigmund等[2]率先提出材料微結構拓撲優化理論，對各向同性材料微結構單胞采用拓撲優化逆向設計技術實現了工程中所需材料特定宏觀性能的微結構構型設計，Neves等[3]基于均勻化方法獲得了周期性線彈性微結構的最優拓撲構型，James等[4]通過對具有最大剛度和流體滲透性的微結構進行設計，實現了材料多功能優化，Huang等[5]基于雙向漸進結構優化法實現了具有最大剪切模量和最大體積模量的微結構拓撲優化．國內學者如劉遠東等[6]基于多尺度均勻化方法開展了周期性復合材料微結構的多目標拓撲優化設計，王寶來等[7]針對輕質材料利用拓撲優化技術實現了最剛微結構構型設計，王憲杰等[8]利用雙向漸進結構優化方法實現了基于宏觀性能的微觀多孔材料拓撲優化設計，汪雷等[9]基于均勻化理論和拓撲優化技術實現了具有最優導熱性能的復合材料微結構拓撲優化設計，張衛紅等[10]基于能量法實現了材料微結構的等效彈性性能的預測，采用對偶凸規劃方法結合周長約束策略進行了微結構構型優化設計．拓撲優化的目的就是確定具有特定性能微觀結構的材料分布，充分發掘材料潛力，從設計的角度提高材料性能．

基于此，本文采用應變能等效的能量法實現材料微結構的等效彈性系數矩陣的求解，然后以等效彈性系數矩陣主對角線上元素的某一項或者某幾項的加權組合為目標，以材料體積率為約束，建立材料微結構的拓撲優化模型．采用SIMP插值及優化準則法求解該優化模型，以敏度過濾抑制數值不穩定現象，實現具有極限彈性性能的最優微結構的拓撲構型優化設計．

1材料微結構的等效性能預測

均勻化方法具有嚴格的數學理論推導，以連續介質理論為基礎，基于擾動理論將物理場按表征微觀結構尺度的小參數漸進展開，從而得到材料微結構的等效彈性性能，但其數學推導繁瑣，計算復雜．基于應變能等效的能量法與均勻化方法相比，其本質相同，但其計算效率高，推導簡潔，編程實現簡便[10]，因此本文將通過應變能等效的能量法求解材料微結構的等效彈性性能．

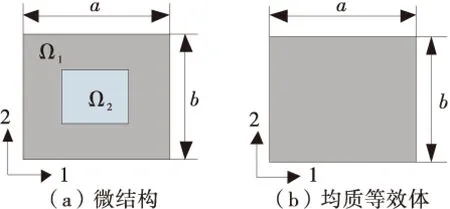
圖1　微結構等效示意圖

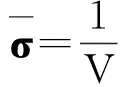
(1)

式中，DH即為微結構的等效彈性系數矩陣．

對于二維正交各向異性材料，式(1)可進一步表示為

(2)

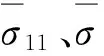
定義微結構的應變能為

(3)

在均勻邊界載荷條件下，材料微結構和均質等效體的彈性應變能應是相等的，由此可得出微結構的單位體積應變能

(4)

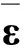
表1　給定工況條件下微結構的應變能

由表1可得材料微結構的等效彈性系數矩陣DH的表達式為

(5)

2材料微結構的拓撲優化模型

基于SIMP插值模型，以單元的相對密度為設計變量，結構整體的體積率為約束，材料微結構的某一項或某幾項極值力學特性為目標，建立如下優化數學模型：

(6)

式中，ωl為加權系數(ωl∈[0，1])；Dll為等效彈性系數矩陣DH的主分量(其中ll=11、ll=22、ll=33分別對應為D1111、D2222、D1212)；V(ρ)為優化后結構的體積；f為體積系數；V0為設計域體積；為防止剛度陣奇異，取最小密度值ρmin=0.001．

3靈敏度分析

有限元平衡方程為

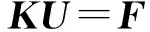
(7)

式中，F、U分別為微結構的結點力向量與結點位移向量．

見表1，在相應邊界條件下(上標n表示邊界條件)的材料微結構應變能為

(8)

由式(7)、(8)可得微結構的應變能對設計變量ρi的導數為

(9)

其中

(10)

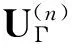
由式(5)得

(11)

按照上述靈敏度的求解方法，結合有限元分析，采用優化準則求解算法即可對上述優化模型進行優化求解，優化流程如圖2所示，其具體步驟如下：

Step1：定義材料微結構設計域，將材料離散到單元；

Step2：材料微結構有限元靜力分析；

Step3：基于能量法求解材料微結構的等效彈性系數矩陣；

Step4：目標函數的計算及敏度分析；

Step5：采用優化準則法對設計變量進行更新；

Step6：根據收斂條件判斷目標函數是否收斂，如果不滿足收斂條件，則重復Step2～Step5，如果滿足收斂條件，輸出結果．

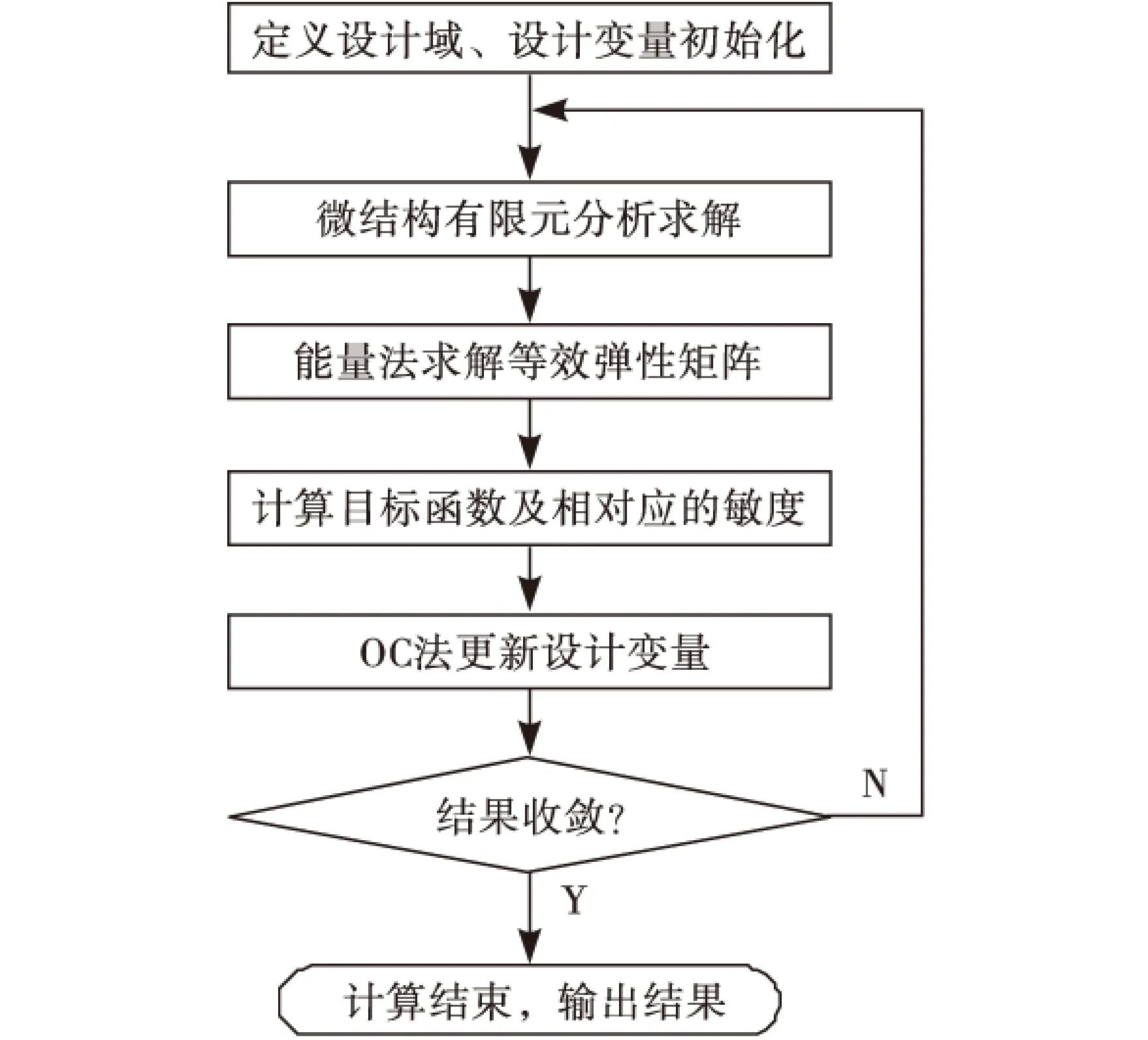
圖2　材料微結構優化設計流程圖

4數值算例及分析

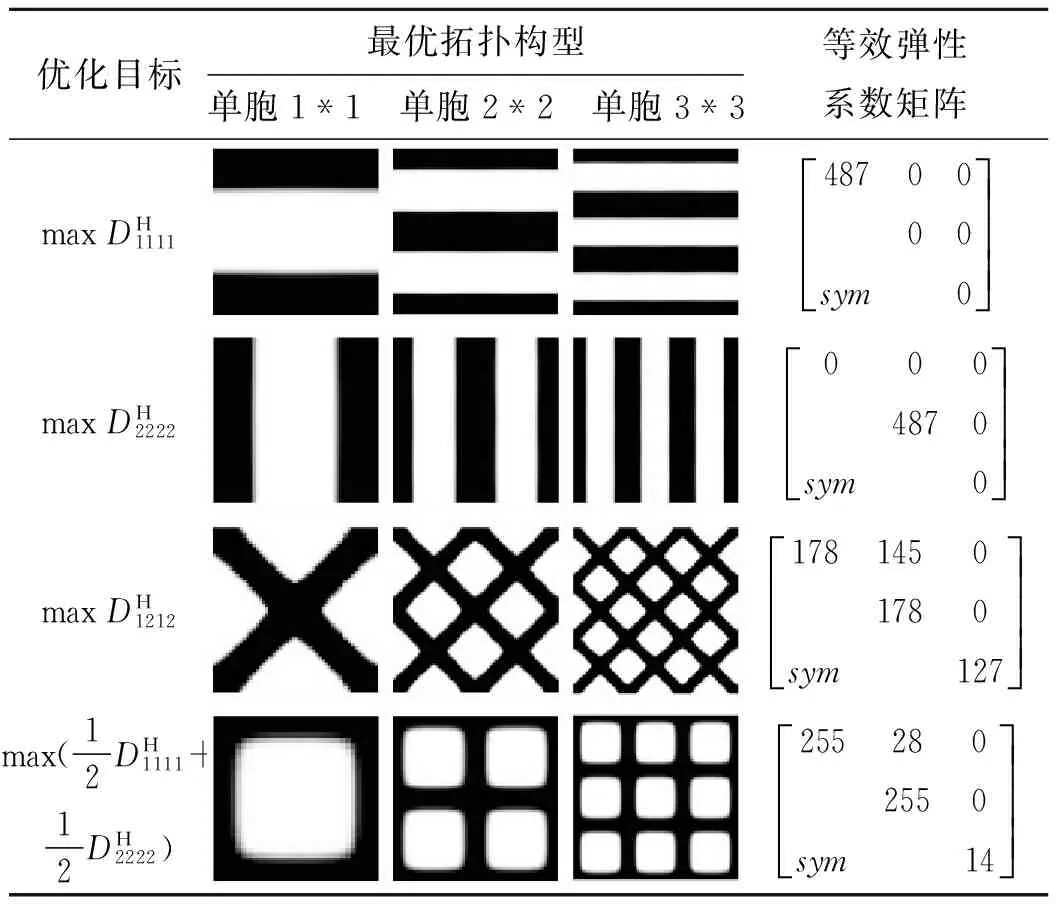
表2　不同優化目標下微結構的最優拓撲構型

由表2可知：

5結語

本文基于應變能等效的能量法求解材料微結構的等效彈性矩陣，以等效彈性矩陣主對角線上元素的某項或者某幾項加權組合最大為目標建立優化模型對微結構進行拓撲優化設計．算例分析表明，采用SIMP插值和優化準則法有效求解了該拓撲優化問題，利用敏度過濾消除了數值不穩定現象，并得到了具有最優水平方向抗拉強度、豎直方向抗拉強度、抗剪切強度和雙向抗拉強度等極限彈性性能的微結構拓撲構型．

參考文獻：

[1]Kim Y Y, Yoon G H． Multi-resolution Multi-scale Topology Optimization-a New Paradigm[J]． International Journal of Solids and Structures, 2000, 37(39)：5529-5559．

[2]Sigmund O. Materials with Prescribed Constitutive Parameters：An Inverse Homogenization Problem[J]． International Journal of Solids and Structures, 1994, 31(17)：2313-2329．

[3]Sigmund O, Torquato S. Design of Materials with Extreme Thermal Expansion Using a Three-phase Topology Optimization Method[J]． Journal of the Mechanics and Physics of Solids, 1997, 45(6)：1037-1067．

[4]James K, Jeam H. Optimizing Multifunctional Materials：Design of Microstructures for Maximized Stiffness and Fluid Permeability[J]． International Journal of Solids and Structures, 2006, 43(22)：7028-7047．

[5]X Huang, A Radman, Y M Xie. Topological Design of Microstructures of Cellular Materials for Maximum Bulk or Shear Modulus[J]． Computational Materials Science, 2011, 50(6)：1861-1870．

[6]劉遠東，尹益輝，胡文軍.周期性復合材料微結構的多目標拓撲優化設計[J]．機械強度，2012，34(4)：527-530．

[7]王寶來，溫鳳春，梁軍.輕質材料微結構構型的拓撲優化設計[J]．哈爾濱工業大學學報，2009，41(1)：76-79．

[8]王憲杰，張洵安.基于宏觀性能的微觀多孔材料拓撲優化[J]．功能材料，2014，45(18)：18078-18082．

[9]張衛紅，汪雷，孫士平.基于導熱性能的復合材料微結構拓撲優化設計[J]．航空學報，2006，27(6)：1229-1233．

[10] Zhang Weihong, Wang Fengwen, Dai Gaoming, et al. Topology Optimal Design of Material Microstructures Using Strain Energy-based Method[J]． Chinese Journal of Aeronautics, 2007, 20(4)：320-326．

[責任編輯張莉]

收稿日期：2016-01-21

基金項目：湖北省杰出青年基金資助項目(No.2013CFA022)；湖北省科技支撐計劃對外科技合作資助項目(No.2015BHE026)

通信作者：杜義賢(1978-)，男，副教授，博士，研究方向為CAD/CAM技術，結構優化與分析．E-mail：duyixian@aliyun.com

DOI：10.13393/j.cnki.issn.1672-948X.2016.02.016

中圖分類號：TH122：TB34

文獻標識碼：A

文章編號：1672-948X(2016)02-0071-04

Topology Optimization for Material Microstructures with Extreme Elastic Properties

Zhang Yan1Du Yixian1,2Du Daxiang1Tian Qihua1

(1. College of Mechanical & Power Engineering, China Three Gorges Univ., Yichang 443002, China； 2. Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance, China Three Gorges Univ., Yichang 443002, China)

AbstractBased on the strain energy equivalent energy method, the equivalent elastic coefficient matrix of the materials microstructure is to solve. With the goal of maximizing the one or several of the weighted combination of the leading diagonal elments in the equivalent elastic coefficient matrix, to the material's volume rate as the constraint, the topology optimization model for the material microstructures with extreme elastic properties is constructed. The SIMP interpolation and optimality criteria method are used to solve the optimization model; and then the sensitivity expression in the process of optimization solution is derived. Finally, the topological configuration of material microstructures with extreme elastic properties is achieved. Some numerical example verifies the validity of the topology optimization model and algorithm.

Keywordsstrain energy-based method;material microstructure;extreme elastic properties;topology optimization;SIMP interpolation