兩相異步電機的數學模型及動態特性仿真

汪　敏

(江漢大學 數學與計算機科學學院， 武漢　430056)

?

兩相異步電機的數學模型及動態特性仿真

汪敏

(江漢大學 數學與計算機科學學院， 武漢430056)

摘要：通過對兩相異步電機繞組結構的分析，在理想化假設的情況下推導了兩相電機的電磁關系，建立了電機在任意速旋轉坐標系dqn下的通用數學模型，并在分析電機數學模型的基礎上，應用搭建模塊法建立了Matlab/Simulink軟件環境下兩相異步電機的動態模型．并以實際應用中的小功率電機為例，對電機運行進行了仿真分析．對其啟動后突加負載及帶負載啟動等多種瞬態過程進行了仿真計算．仿真結果表明應用此數學模型對電機運行過程進行仿真具有較高的精度、較好的通用性等優點，具有一定的實用價值．

關鍵詞：兩相異步電機；dq變換；Simulink仿真

0引言

小功率單相異步電機在家用電器和工農業生產中獲得了廣泛應用[1-3]，如水泵、空調、洗衣機等設備所采用的單相異步電機結構具有結構簡單、控制方便、運行可靠等優點．小功率異步電機很多場合都希望能調節速度，比如空調用電機運行于高精度溫度調節、洗衣機運行于洗衣或者甩干模式時，都希望電機能在很寬的范圍內調節速度，同時又希望電機的輸出轉矩不要出現太大的波動，很顯然單相電機偏軟的機械特性已不能滿足實際需求，由于單相電機只有一個主繞組，通電后所產生的磁場是脈振磁場，不是旋轉磁場，不能使鼠籠式轉子產生啟動轉矩．因此一般利用電容啟動的單相異步電機都設置了一個在空間上與主繞組相差90°電角度的副繞組，利用交流電路中電容的電流超前電壓90°相角這一原理產生旋轉磁場．單相異步電機的這種結構導致調速控制方法受到很大的限制，實際控制中一般采用較為簡單的調壓或調頻的方式，其轉速調節密度較低，導致效率低、經濟性差；在實行變頻調速時，頻率變化將導致電機內部磁場由圓形變成橢圓，造成轉子轉矩波動，電機運行效率降低，不能滿足家電和工業用電機不斷增長的性能需求[4-6]．

而采用對稱繞組的兩相異步電機則可以解決以上這些問題，兩相異步電機內部有兩個主繞組，可用變頻器輸出對稱兩相電壓來直接驅動，因此可以實現精確、靈活而連續的速度控制，并且運行非常平穩．隨著電力電子技術、微處理器及現代控制技術的發展，實現兩相異步電機的變頻調速系統非常方便，同時具有結構簡單、運行可靠、調速性能好、工作壽命長等優點．既可以獲得和三相異步電機相近的動態性能，結構又相對簡單．

1兩相異步電機參數的確定

兩相異步電機繞組由定子繞組和轉子繞組兩部分構成，定子繞組采用相差90°電角度的結構，轉子繞組采用鼠籠式結構．兩相異步電機是一個高階、強耦合、非線性的多變量系統，其基本結構如圖1所示，由理想化電機的假設可以推導出兩相異步電機的繞組電感．

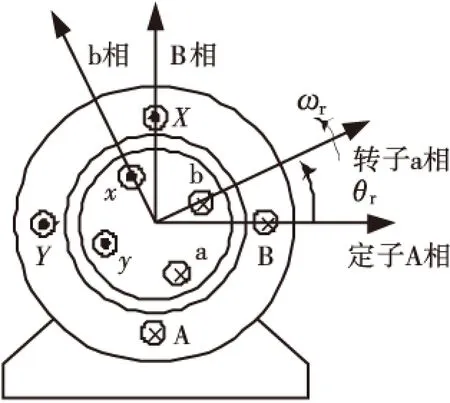
圖1　兩相異步電機結構

異步電機的基本模型參數計算中，對于p對極電機x相繞組和y相繞組電感系數lxy的一般化計算公式為[2]：

(1)

式中，Λg為氣隙磁導，Nx，Ny分別為x繞組和y繞組的匝數，αxy為x繞組和y繞組軸線的夾角．

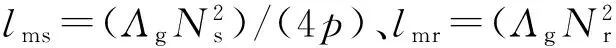
(2)

定、轉子繞組之間的互感矩陣為：

(3)

式中，θr為定、轉子繞組之間夾角．可以看出兩相異步電機與三相異步電機的數學模型的區別在于兩相電機定子繞組兩相之間和轉子繞組兩相之間互感為零，消除了耦合．

2dqn坐標系中的數學模型

建立旋轉坐標系如圖2所示[2]，從相坐標系到dq坐標系的變換矩陣為：

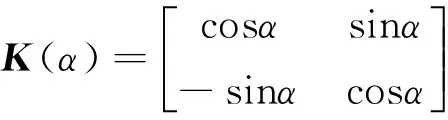
(4)

式中，α為d軸與定(轉)子A(a)相繞組軸線之間的夾角．

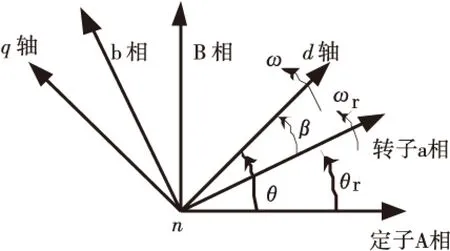
圖2　相坐標系和dq坐標系

由旋轉變換得dq坐標系中的磁鏈方程為：

(5)

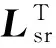
(6)

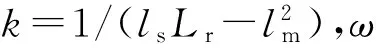
3靜止坐標系下模型的構建

忽略電機內部的鐵磁損耗及磁飽和等因素可以簡化電機模型，在靜止坐標系中以定子電流和磁鏈作為狀態變量建立兩相鼠籠式異步電機的動態數學模型，由式(6)中的數學模型[7-8]得兩相異步電機在αβ靜止坐標系下的表達式：

(7)

(8)

電磁轉矩和轉子運動方程為：

(9)

(10)

式中，Te、TL為電磁轉矩、負載轉矩；np為電機極對數；J為轉子轉動慣量．

可以在Simulink中利用豐富的模型庫建立兩相鼠籠式異步電機的數學模型，將電機模型分解為獨立的子模塊，由式(7)(8)建立定子側α軸電流、磁鏈仿真子系統如圖3所示，類似地可以建立定子側β軸電流、磁鏈仿真模塊、轉子側α軸電流、磁鏈仿真模塊和轉子側β軸的電流、磁鏈仿真模塊如圖4～6所示．

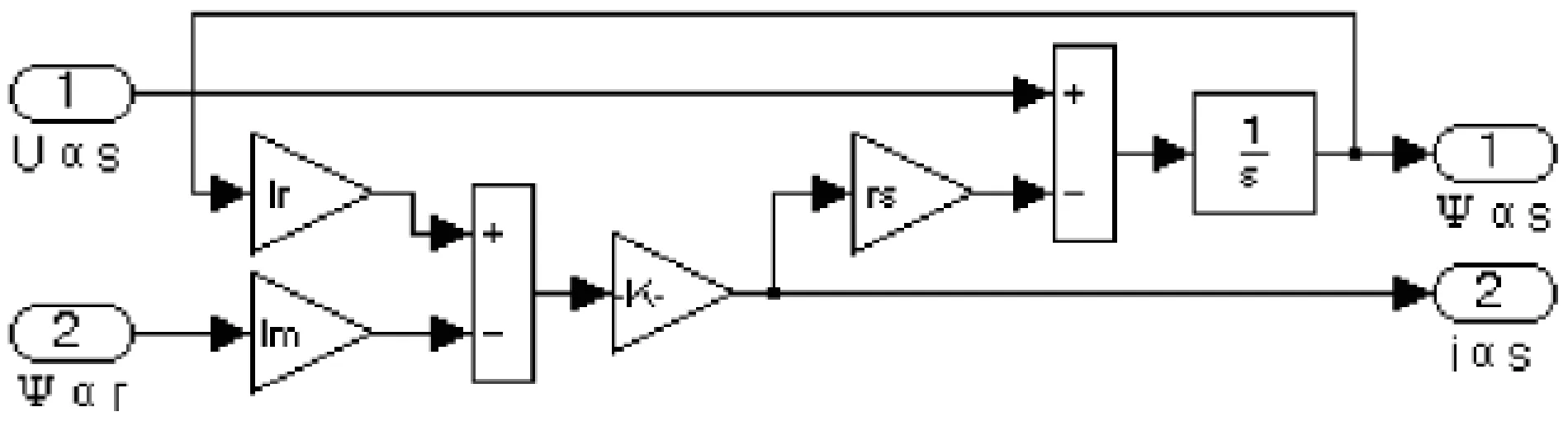
圖3　定子側α軸的電流、磁鏈仿真子系統

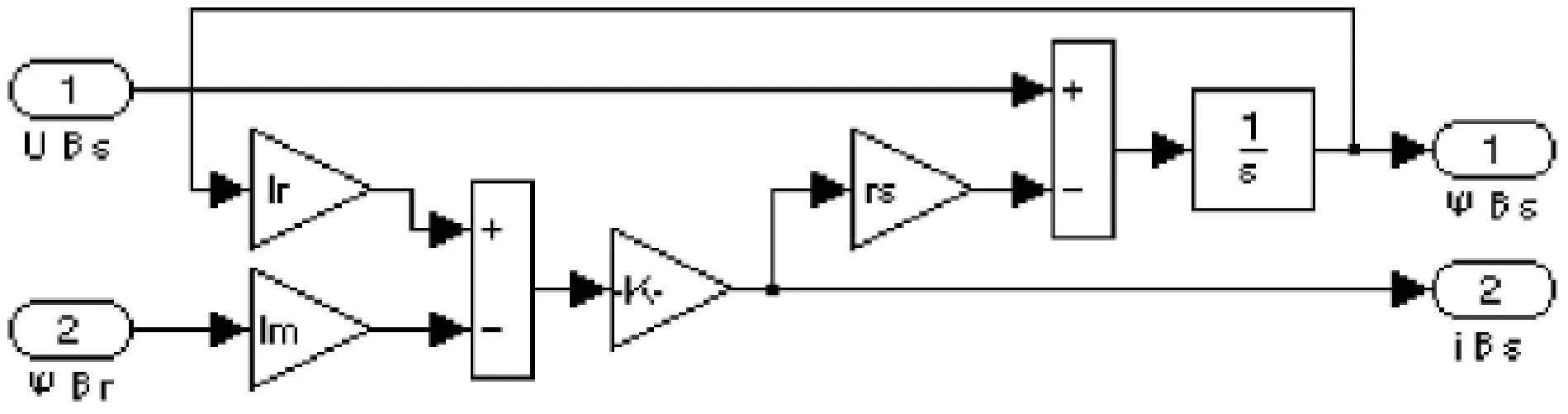
圖4　定子側β軸的電流、磁鏈仿真子系統

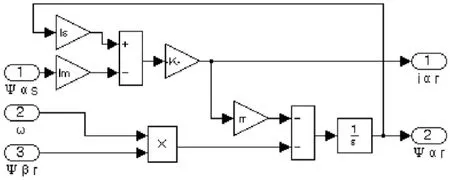
圖5　轉子側α軸的電流、磁鏈仿真子系統

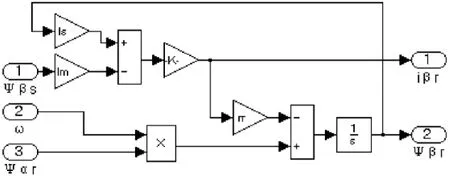
圖6　轉子側β軸的電流、磁鏈仿真子系統

根據兩相異步電機數學模型中的電磁轉矩方程式(9)(10)，可建立電機電磁轉矩及轉子運動仿真子系統如圖7所示，圖中Te為電機輸出轉矩，TL為負載轉矩．

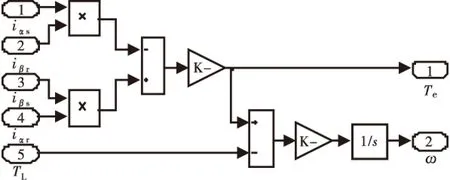
圖7　電磁轉矩仿真子系統

由兩相異步電機的數學模型和Simulink信號流圖，可以建立兩相異步電機的仿真模型如圖8所示．

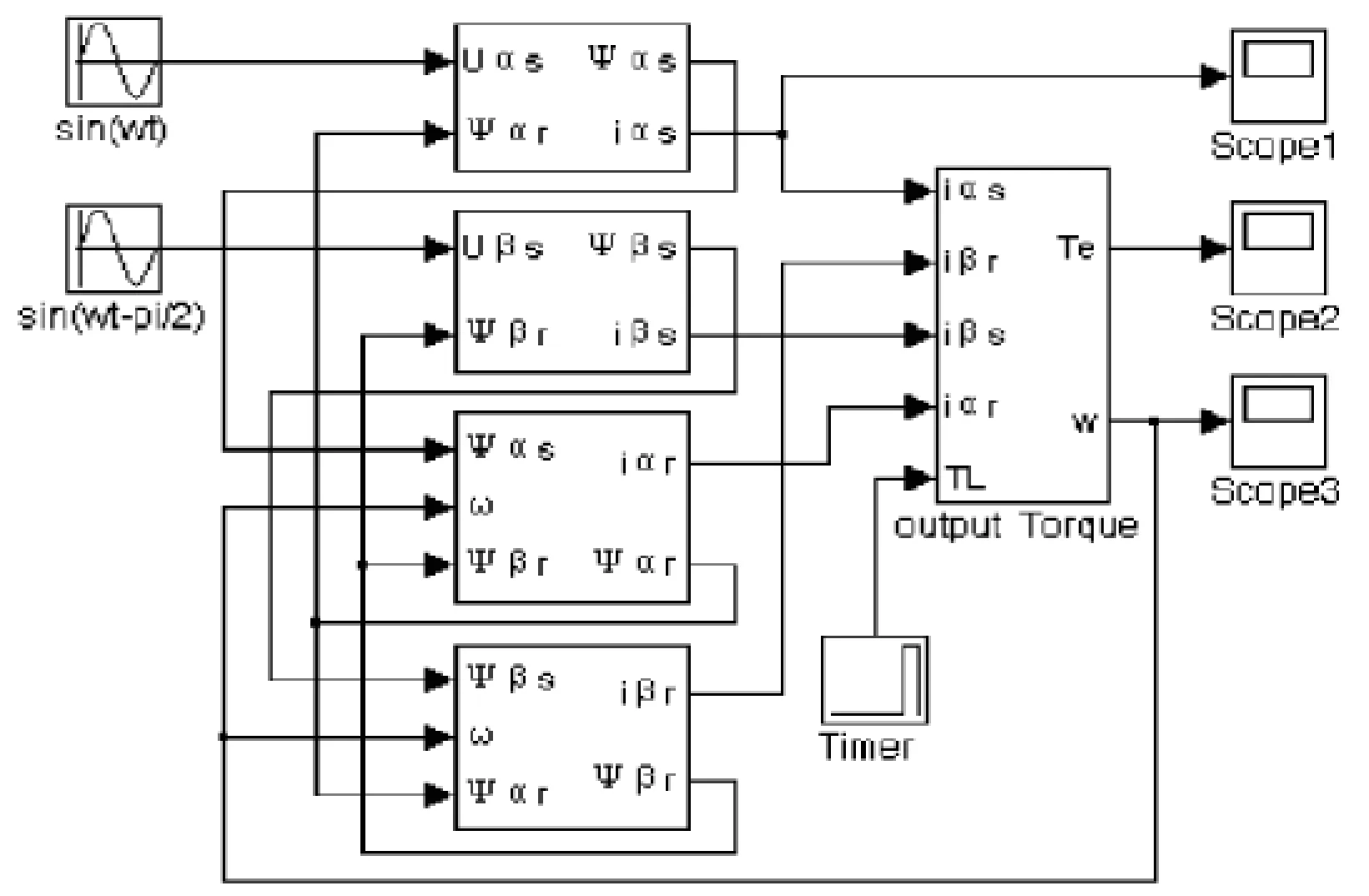
圖8　兩相異步電機的仿真模型

4實例仿真

1) 空載啟動，在0.5～0.6 s時間段加上6 N·m負載，定子A相電流、電磁轉矩Te、轉子轉速ω如圖9所示．

圖9　空載啟動后加負載的仿真波形

空載啟動時，起動過程沖擊電流較大，幅值可達額定值的4倍，電機轉速在0.3 s左右上升到額定值，0.5～0.6 s加上負載時電機轉速開始下降，電磁轉矩迅速上升，具備很強的轉矩跟蹤能力，負載波動造成的影響能很快消除，轉速下降幅度很小，并能很快恢復到穩定值．這主要是由于電機具備較大的慣性，穩定運行時態已存儲一定的電磁能和機械能，因此負載突變造成的影響不明顯．

2)電機帶負載啟動，負載轉矩為6 N·m，a相電流、電磁轉矩Te、轉子轉速ω仿真結果如圖10所示．

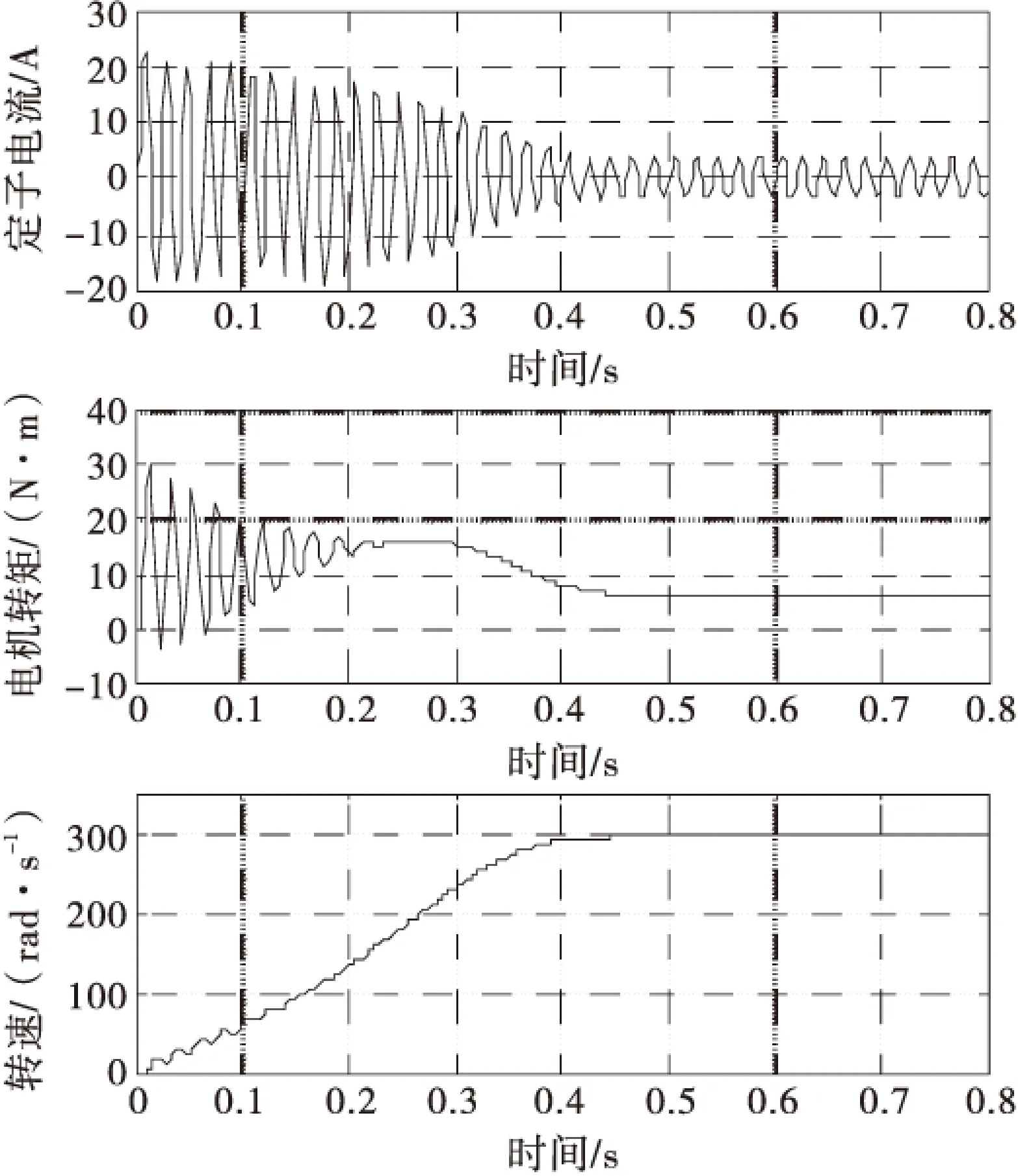
圖10　帶負載啟動時的仿真波形

帶負載啟動時電機沖擊電流比較大，和空載啟動時相比電流持續時間和轉速上升到穩定值的時間都相對有所延長，大概需要0.4 s左右，有轉矩擾動時，兩相異步電機只需0.2 s左右就能達到新的穩態．在啟動轉矩波動及穩定性方面有很大提升．仿真結果驗證了模型的有效性，由于兩相異步電機的定子磁鏈軌跡接近圓形，啟動轉矩大，轉速上升快，消除了單相異步電機中脈動磁場缺陷而導致的較大幅度的轉矩脈動，運行更加平穩，理論上穩態運行可以保證機械轉矩恒定；同時兩相結構和單相相比，具有較大的空間利用率，可以獲得更大的功率密度，因此可以獲得較強的帶載能力，帶負載啟動時，電流和轉矩脈動較小；穩態運行時，抗干擾能力也很強．

目前單相異步電機的控制主要通過控制電磁轉矩和磁鏈來實現，將轉矩和磁鏈經坐標變換后等效為直流電機進行控制．由于主副繞組匝數的不對稱性，磁鏈矢量不能以固定幅值旋轉，使電機內部磁場為橢圓型磁場而非圓形磁場，因此單相異步電機運行中轉矩脈動較大．而采用兩相模型的異步電機系統，很好地消除了磁場脈振、轉矩脈動過大等問題，由數學模型可知兩相結構內部磁場為圓形磁場，穩態運行沒有轉矩脈動，采用兩相結構的電機模型具有良好的運行穩態性能，控制精度高，實用性較好．

5結語

介紹了兩相異步電機矢量變換的數學模型，并在Simulink環境下建立了電機的數學模型并完成了仿真分析，采用該兩相異步電機的仿真模型，可以十分便捷地對兩相電機的啟動性能進行了分析和仿真，得出該交流電機的轉矩、轉速等運行曲線，波形符合理論分析．

仿真結果表明兩相異步電機具有較好的靜態、動態性能，同時兩相異步電機驅動系統可由變頻器直接產生對稱兩相電壓，直接驅動兩相繞組，采用對稱繞組的兩相異步電機和三相異步電機相比，結構相對簡單，卻能夠獲得和三相異步電機相近的動態性能．兩相異步電機可以克服單相電機轉矩脈動的情況，在功率較大的情況下有明顯的優勢，可應用在空調、水泵等設備上，能在滿足性能要求的前提下降低系統成本．

參考文獻：

[1]傅海濤,楊長安．兩相異步電機的動態特性仿真[J]．中小型電機，2005，32(4)：10-13．

[2]辜承林.機電動力系統分析[M]．武漢：華中科技大學出版社，1998．

[3]顧德英，季正東，張平．基于Simulink的異步電機的建模與仿真[J]．電力系統及其自動化學報，2003，15(2)：71-73．

[4]Yu X，Dunnigan M W，Williams B W．A novel rotor resistance identification method for an indirect rotor flux orientated controlled induction machine system[J]． IEEE. Transactions on Power Electronics，2002，17(3)：353-364．

[5]Avdiu N Z． Modeling of the induction motor with two sets of three phase windings in the stator and squirrel cage rotor. IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society[J]． IEEE Conference Publications, 2012 , 1900-1907．

[6]楊祖泉，姚緒梁，舒小芳．異步電動機直接轉矩控制系統的仿真研究[J]．電機與控制學報，2004,8(4)：329-332．

[7]周力求，等．基于MATLAB/SIMULINK的異步電動機建模與仿真[J]．電機電器技術，2003(4)：32-35．

[8]Jezernik K． Robust Induction Motor Control for Electric Vehicles. Advanced Motion Control[C]． Tsu-City, Japan：1996. AMC '96-MIE. Proceedings．

[責任編輯張莉]

收稿日期：2015-09-06

通信作者：汪敏(1979-)，女，講師，博士，研究方向為計算數學．E-mail： wangmin_6@163.com

DOI：10.13393/j.cnki.issn.1672-948X.2016.02.017

中圖分類號：TM343

文獻標識碼：A

文章編號：1672-948X(2016)02-0075-04

Dynamic Simulation and Mathematical Model of Two-Phase Asynchronous Motors

Wang Min

(School of Mathematics & Computer Science, Jianghan Univ., Wuhan 430056, China)

AbstractBased on analyzing the winding structure of two-phase asynchronous motor, the electrical and magnetical relationship has been deduced under an ideal assumption. The universal mathematical model under dqn coordinate turning at arbitrary angular velocity has been established. The simulation case of the two-phase asynchronous motor has been constructed under Matlab/Simulink environment. The starting and loading conditions have been simulated. The results demostrate that the two-phase asynchronous motor has characters of high accuracy and stability.

Keywordstwo-phase asynchronous motor；dq trasformation；Simulink