約束阻尼板的漸進法結構減振拓撲動力學優化

賀紅林，陶　結，袁維東，肖智勇

（南昌航空大學 航空制造工程學院，南昌 330063）

?

約束阻尼板的漸進法結構減振拓撲動力學優化

賀紅林，陶結，袁維東，肖智勇

（南昌航空大學 航空制造工程學院，南昌 330063）

摘要：旨在為結構減振設計奠定一定基礎，研究約束阻尼板減振優化問題。建立約束阻尼板動力學平衡方程，推導模態損耗因子計算模型。構建以模態損耗因子最大為目標，黏彈性材料用量及模態頻率變動最小為約束的阻尼板拓撲優化數學模型，推導模態損耗因子靈敏度算式。引入漸進結構優化方法對約束阻尼板動力學優化模型進行求解，采用獨立網格濾波技術，解決優化迭代中出現的棋盤格問題。編制阻尼板拓撲優化程序，實現約束阻尼板減振優化。仿真顯示，與非優化刪除方法相比，采用漸進拓撲動力學優化，更有利于實現黏彈材料優化布局，且模態頻率變化比較穩定。對阻尼結構進行諧響應分析，以驗證拓撲優化方法有效性，引入模態損耗因子體積密度指標以評價阻尼板減振拓撲優化性能。研究表明，若能實現結構模態損耗因子最大化，約束阻尼板減振效果明顯。該方法對于約束阻尼板設計具有較強實用性，擁有較高的穩定性。

關鍵詞：振動與波；約束阻尼板；模態損耗因子；棋盤格；動力學優化

隨著航空航天等現代科技的迅猛發展，機械日益朝著高速度、大動力、輕量化方向發展，使機器的結構變得越來越復雜，運轉環境更為惡劣，從而愈加容易受外界振動的干擾。劇烈的振動將會導致諸多不良危害，如造成機器工作精度下降、振動疲勞、損壞，并產生噪聲等問題[1–3]。如何高效控制結構振動已成為機械設計的重要課題。由于具有良好減振性能，在結構表面敷設阻尼材料是抑制振動的重要方法之一[4]。附加阻尼結構作為常用的有效阻尼減振結構形式，被廣泛應用于振動控制中，附加阻尼結構有自由阻尼層和約束阻尼層兩種。自由阻尼層主要通過阻尼材料拉伸變形來消耗結構能量，而約束阻尼層通過阻尼材料剪切以耗能。若在結構表面全部敷設阻尼材料，可最大限度地降低振動，但必然帶來結構質量增大的問題，這對飛機等質量敏感性結構，是不可接受的。為此，必須在保證最佳減振效果，確定阻尼材料優化布局的同時，減少阻尼材料用量。張志飛基于變密度法，建立自由阻尼結構優化模型并通過實驗驗證了方法的有效性[5]。胡衛強等建立在諧和激勵條件下，自由阻尼板材料優化配置模型，能夠有效控制振動[6]。王明旭基于變密度拓撲優化方法[7]，獲得結構的最優拓撲構形。鄭玲基于優化準則構建以模態阻尼比為目標函數的拓撲優化模型獲得約束阻尼結構最優構型[8]。郭中澤采用密度法和RAMP插值模型建立的阻尼板結構拓撲優化數學模型得到最優分布構形[9]。李攀基于SIMP插值模型和變密度法對阻尼板進行拓撲優化，顯著降低頻響幅值[10]。變密度法和準則法等數學意義嚴格，但實際應用會遇到較大困難。為此，Xie提出結構漸進法，該方法盡管數學意義不甚嚴格但易于實現、較具實用性[11]。實踐表明，自由阻尼結構耗能方式效率較低，約束阻尼結構則能消耗更多的機械量[12]，同時，薄板結構在工程上應用較為廣泛，研究薄板結構減振有著較大的理論意義和工程實際應用價值，故本文采用研究約束層阻尼板的漸進拓撲優化問題。

1　模態損耗因子建模

約束阻尼板由基層、黏彈阻尼層及約束層構成，主要利用阻尼層的剪切效應來耗散結構的振動能，借助約束層來強化減振效率，其減振特性可用模態損耗因子予以評價，為此有必要推導其損耗因子計算模型。根據振動理論，約束阻尼板動力學平衡方程可寫成

式中M是阻尼板質量矩陣；C為板的阻尼矩陣；K為阻尼板剛度矩陣；X為位移向量；Q為外加在阻尼板的激勵載荷向量。復剛度法對黏彈阻尼材料特性采用復模量模型進行描述，并將黏彈性阻尼材料的彈性模量定義為復數形式[13]

式中E為阻尼層復彈性模量；E′、E″為阻尼材料的實剛度和虛剛度；ηv是阻尼材料損耗因子。考慮約束阻尼板的構成并引入復剛度模型后，可將阻尼板動力學方程改寫成

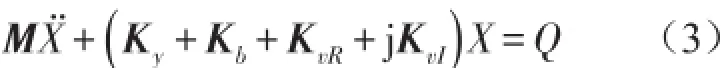
式中Ky表示約束層剛度矩陣；Kb表示基層剛度矩陣；KvR表示黏彈性層剛度矩陣實部；KvI表示黏彈性層剛度矩陣虛部。采用模態法求解式（3）時，可寫出阻尼板的自由振動解形式

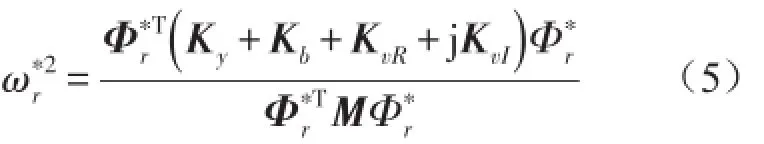
式中Φ?r是阻尼板r階復模態振型，為r階復圓頻率，且復圓頻率可由瑞利商求得Rao推導出模態損耗因子與復圓頻率間關系[14]式中ωr為r階復模態圓頻率的實部；ηr為第r階模態損耗因子。考慮到約束阻尼板彈性特質的主導性，故在計算精度要求不是特別高的情況下，Φ?

r可用實模態振型Φr近似替代，則由式（5）可得第r階近似圓頻率

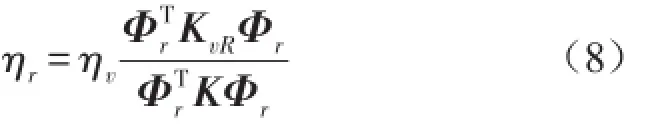
式中K（=Ky+Kb+KvR）為阻尼板總剛矩陣。

將式（6）代入式（7），得模態損耗因子計算式

2　結構動力學優化建模

2.1優化數學模型

合理地設計約束阻尼板的黏彈層及約束層平面敷設形貌，可望最大程度地發揮黏彈層的減振效能，并減少阻尼板的質量。從減少結構振動能的意義上講，既可擇取阻尼板振動響應幅值為量化的優化目標，也可選取模態阻尼比、模態損耗因子、動撓度等為目標。眾所周知，特定階次模態損耗因子全方位地反映結構耗散該階次振動響應能力，這說明，只要合理規劃阻尼層和約束層形貌及其敷設位置可提高結構在激振頻區內的振動模態損耗因子，即能使阻尼板獲得較佳減振效果。或換個角度講，為保證阻尼板減振效果及輕量化設計要求，可基于模態損耗因子最大化的目標，規劃黏彈性層與基層的幾何布局。值得注意的是，在保證減振特性的同時，如何最大程度地保證結構動態特性，比如結構模態頻率等保證基本不變，也是在結構動學設計時必須關注的方面。基于上述考慮，為最大限度地消耗振動能量，以模態損耗因子最大化為目標，阻尼材料用量和模態頻率變動最小為約束條件，建立了阻尼板的拓撲優化數學模型

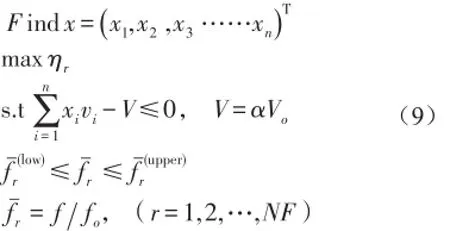
其中xi=[0，1]為拓撲設計變量，表征第i個黏彈阻尼單元在優化迭代后的狀態，xi取值為0時表示該單元已刪除，為1時則表示該單元繼續保留，n為粘彈性單元網格化數量，vi、Vo分別表示粘彈性單元i的體積與粘彈性材料總體積，α表示體積分數。 f、fo分別為優化前和拓撲迭代后第r階模態頻率，fˉr表示第r階歸一化頻率，fˉ(low)r、?fˉ(upper)r分別表示歸一化

頻率的上下限。NF表示需控制頻率變化范圍的模態數量。

2.2損耗因子靈敏度

采用漸進優化法求解模型式（9）。該方法建立在目標函數對設計變量求導基礎上，為目標導數型方法，即為求解式（9）須推導出模態損耗因子關于設計變量的靈敏度。實際上，該靈敏度不僅是拓撲優化的評判依據，更重要的是為迭代搜索提供方向。有了損耗因子靈敏度，可較易地尋得優化構型。為此，令式（8）對設計變量求導，從而得到模態損耗因子靈敏度

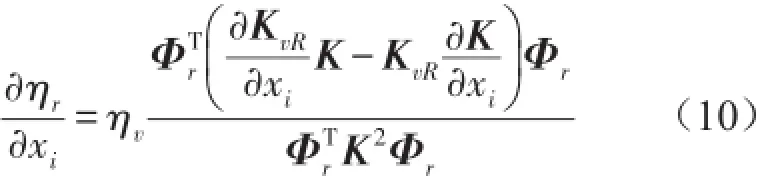
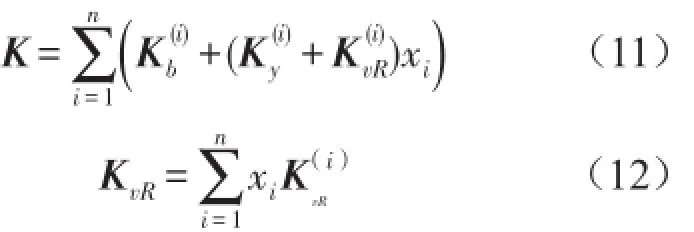
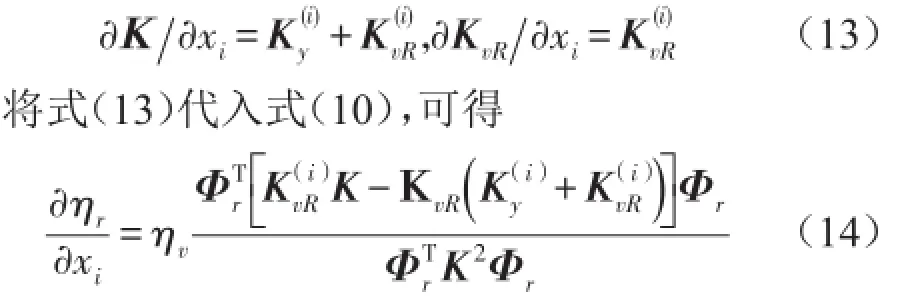
式（14）表示阻尼材料單元i及相應約束層單元刪除后導致約束阻尼結構模態損耗因子的變化量。則第r階約束阻尼單元i的靈敏度可定義為

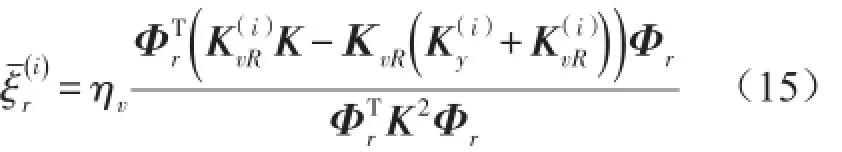
2.3頻率約束靈敏度

約束阻尼結構在優化設計過程中，必須滿足頻率約束條件的限制，而阻尼結構復雜，若僅憑借經驗進行拓撲優化設計，較難達到模態變動最小的要求，為解決該問題，可進行頻率靈敏度分析，以提高優化效率。

根據結構動力學理論，可得以下方程式

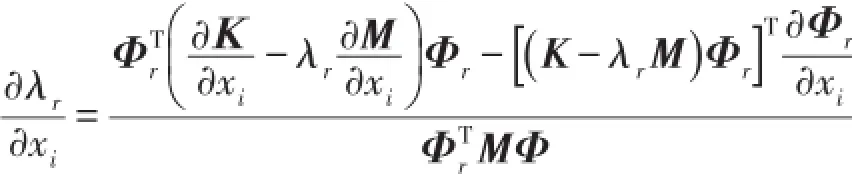
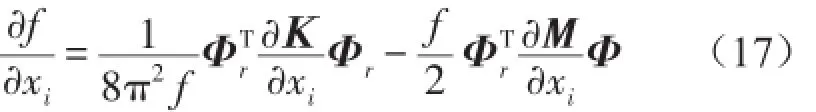
式（17）即模態頻率 f對設計變量xi變化的敏感程度。若結構出現重頻時，靈敏度分析推導更復雜一些。

2.4獨立靈敏度濾波

采用漸進結構優化進行連續體靜力學拓撲優化時引來一個重要問題是會出現數值不穩定現象，其主要表現是棋盤格式、網格依賴癥等。約束阻尼板漸進減振動力學優化將面臨同樣的問題。為了克服上述現象，本文擬采用Sigmund[15]獨立網格濾波技術消除數值不穩定現象。該技術是一種簡單適用的啟發式算法，它以所分析的單元為中心，對過濾半徑范圍內所有單元靈敏度進行加權求和，且以加權值作為該單元的靈敏度。優化時以靈敏度均化值決定單元的刪留表示單元i濾波前的靈敏度，Hi=Rmin-dist(i,e），Hi是權重因子，Rmin是濾波半徑，dist(i,e)表示單元i和單元e的中心距離，N表示單元e的中心距離dist(i,e）不大于Rmin的單元總數。選擇合適的濾波半徑，能夠有效消除棋盤格式和網格依賴癥等現象。

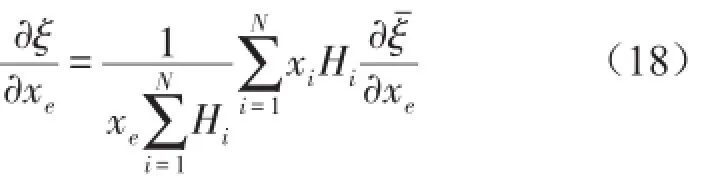
3　優化模型的求解

約束阻尼板拓撲減振優化的實質就是逐步刪除靈敏度絕對值較小的單元，在減小阻尼材料用量的情況下，實現模態損耗因子最大化。運用ANSYS的APDL語言編制優化程序，使用Debug命令提取矩陣，形成OUT文件，清除單元編號、行編號、注釋等，以數組方式輸入MATALB中，處理和計算完成后，以共享數組方式實現與ANSYS數據傳遞。圖1給出了優化數學模型求解程式，即

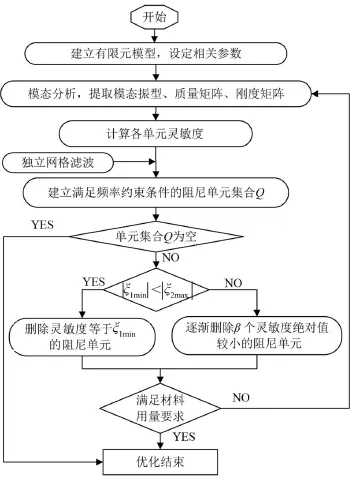
圖1　約束阻尼材料拓撲優化程序流程圖

（1）建立約束阻尼板有限元分析模型，確定阻尼板邊界條件以及各相關參數；

（2）進行結構模態分析。提取約束阻尼板的質量矩陣、剛度矩陣、模態振型，將數據導入MATLAB中，分別按式（15）、式（17）進行損耗因子靈敏度和頻率約束靈敏度計算，經處理后將數組返回ANSYS；

（3）選擇合適的濾波半徑，按式（18）對損耗因子靈敏度進行獨立網格濾波處理；

（4）判斷頻率約束靈敏度值，構建符合頻率約束條件的黏彈性阻尼單元集合Q，若單元集合為空，則優化結束，否則繼續優化迭代；

（5）對單元集合Q中損耗因子靈敏度值進行排序，提取正靈敏度中最小值ξ1min和負靈敏度中最大值ξ2max；

（6）當||ξ1min小于||ξ2max，刪除靈敏度等于ξ1min的黏彈性單元，當||ξ1min大于或等于||ξ2max，則按由小到大原則逐漸刪除β個損耗因子靈敏度絕對值較小的單元；

（7）若滿足材料用量要求，則優化結束，否則重復步驟（2）至（7），直到滿足材料用量要求退出優化迭代。

4　算例分析

為驗證優化算法的有效性，針對矩形結構約束阻尼板進行漸進優化仿真，該板的長度和寬度均設定為0.5 m，基層厚0.004 5 m，基層彈性模量設定為70 GPa，泊松比為0.34，密度為2 700 kg/m3；黏彈性層彈性模量為12 MPa，泊松比0.495，密度為1 200 kg/m3，阻尼損耗因子0.5，黏彈性層厚0.001 5 m。約束層各項參數與基層基本相同，只是約束層厚為0.001 5 m。

分別以黏彈性材料刪除率為25%、50%作為迭代終結點對約束阻尼板的漸進優化迭代過程進行跟蹤，且為便于對比，在圖2給出了僅按單元序號刪除黏彈材料的非優化結果。圖3則給出了對應于上述兩種黏彈材料刪除率的阻尼板優化布局。

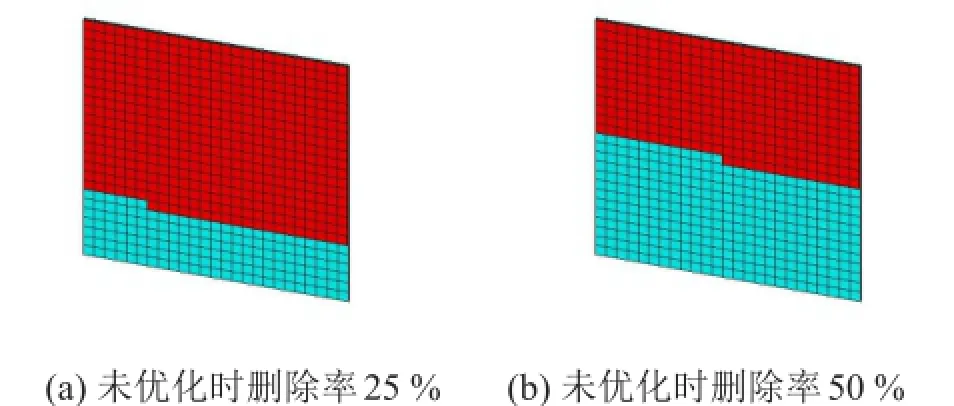
圖2　約束阻尼板未優化時的布局

圖3　約束阻尼材料優化布局

圖3（a）、（b）是針對1階模態損耗因子進行優化時的黏彈性阻尼材料的優化布局，在刪除率為25% 和50%的情況下，搜尋阻尼材料最優布局，優化過程中，逐漸刪除處于無效或低效狀態的單元，保留高效單元。從圖3看出，優化布局邊界清晰，獨立網格濾波技術很好地解決了優化過程中的棋盤格等問題。

圖4給出了基于損耗因子最大化為目標，1階和2階損耗因子變化，同時給出了阻尼材料按單元序號刪除的非優化損耗因子變化。隨著刪除率的不斷增大，按漸進法刪除阻尼材料，損耗因子雖有一定程度下降，但降幅不大，而按非優化方法刪除阻尼材料，模態損耗因子在非優化的后半段逐漸劇烈下降。可見，若基于漸進法，優先刪除靈敏度較小的阻尼單元，可使結構以較少的材料獲得較好的減振能力。因此合適的優化方法和阻尼材料布局，可盡可能的提高結構模態損耗因子，更好地提高結構抑制振動的能力。

圖5給出了模態頻率隨刪除率的變化。可見，隨著迭代不斷進行，阻尼材料不斷刪除，基于優化法的模態頻率變化比較穩定，而未優化時頻率均呈現先降后升的趨勢，頻率變化劇烈。刪除率為50%時，1階、2階優化后頻率變動均比未優化時小，驗證了優化結果的有效性。因此，相比較于未優化的刪除方法，基于漸進法逐漸刪除阻尼材料，結構特定階次的頻率并無很大幅度的變化，同時還滿足頻率約束的要求。

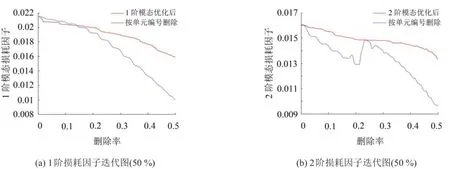
圖4　約束阻尼模態損耗因子隨刪除率的變化

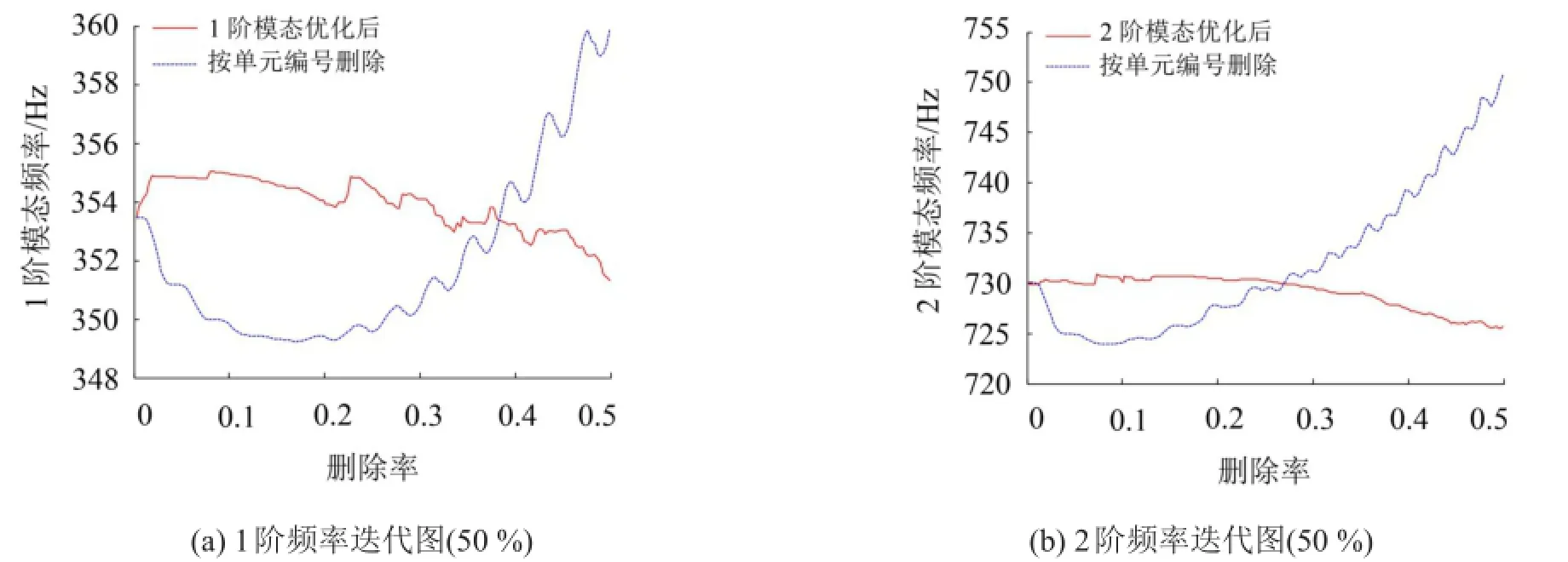
圖5　約束阻尼模態頻率隨刪除率的變化

圖6給出了阻尼結構在優化前后的諧響應特性變化。圖中可見，若分別按1階模態、2階模態優化時，即使阻尼材料刪除率達50%也能保證優化后的1階、2階模態振幅值均有一定程度下降，故而驗證了優化方法的可行性，也表明基于漸進法的阻尼結構優化，可使結構獲得良好的減振特性。

為定量評價約束阻尼板黏粘彈材料優化前后耗能效能，引入損耗因子體積密度的概念，并將其定義為模態損耗因子與阻尼材料體積之比。

圖7（a）、（b）給出了1階、2階模態損耗因子體積密度的變化曲線，隨著低效阻尼單元不斷刪除，保留在阻尼板上的都為高耗能單元，能最大程度發揮阻尼材料減振效能，故1階、2階模態損耗因子體積密度均呈現直線上升趨勢。若不進行優化，按單元編號逐漸刪除阻尼單元，1階、2階損耗因子密度均呈現先升后降的趨勢，且其值比優化時小，表示此時阻尼材料并未較好地發揮減振效能。以上分析進一步表明在設計阻尼板減振結構時，采用基于模態損耗因子最大化的漸進優化方法有利阻尼材料優化布局，能充分發揮阻尼材料減振效果。

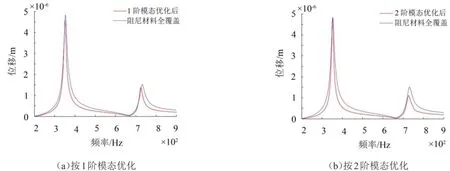
圖6　阻尼結構諧響應分析

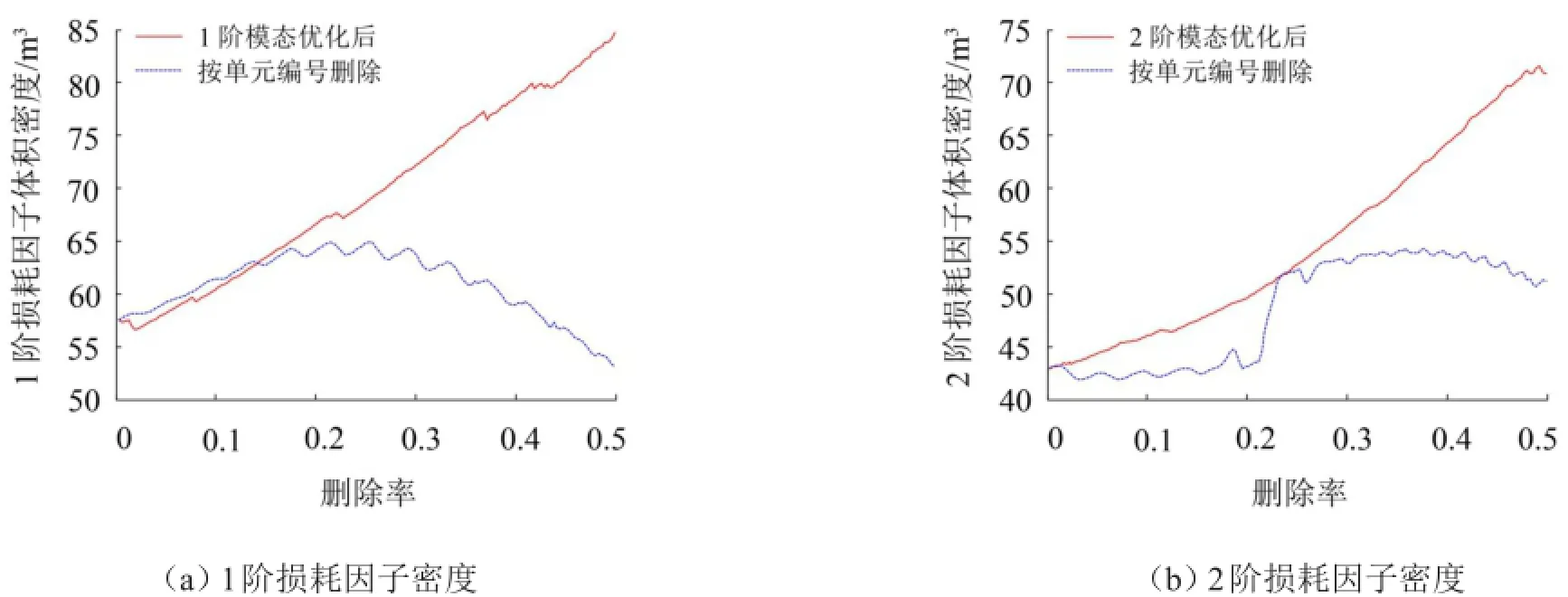
圖7　模態損耗因子密度隨刪除率的變化

5結　語

基于漸進法對約束阻尼板拓撲減振優化方法進行了研究。依據阻尼板動力學平衡方程，推導了模態損耗因子計算模型，建立結構動力學優化數學模型，給出模態損耗因子靈敏度計算方法。采用獨立網格濾波技術，有效消除棋盤格等現象，編程實現了矩形板拓撲漸進減振動力學優化算法，并基于漸進算法對優化模型進行求解，同時為評價約束阻尼板減振優化效果，引入模態損耗因子體積密度指標。研究結果表明，通過與非優化刪除方法進行比對，本文提出的漸進優化算法，能在保證黏彈材料用量較小，結構模態頻率變動最小的前提下，使結構獲得良好的減振效果。

參考文獻：

[1]劉文光，李俊.含裂紋平板的振動及裂紋擴展分析[J].噪聲與振動控制，2013，33(6)：168-171.

[2]賀紅林,，周楠蘭，袁維東.基于復合模態阻尼比的阻尼板漸進法減振優化[J].工程設計學報，2015，22（4）：351-358

[3]張宗成，楊景玲，張燕，等.發動機油底殼的噪聲分析及結構優化[J].噪聲與振動控制，2013，33(6)：115-119.

[4]趙靜，周鋐，梁映珍，等.車身板件振動聲學貢獻分析與優化[J].機械工程學報，2010，46(24)：96-100.

[5]張志飛，倪新帥，徐中明，等.基于優化準則法的自由阻尼材料拓撲優化[J].振動與沖擊，2013，32(14)：98-102.

[6]胡衛強，葉文，曲曉燕.諧和激勵下阻尼材料的配置優化[J].噪聲與振動控制，2013，33(4)：40-43.

[7]王明旭，陳國平.基于變密度方法約束阻尼層動力學性能優化[J].南京航空航天大學學報，2010，42(3)：283-287.

[8]鄭玲，謝熔爐，王宜，等.基于優化準則的約束阻尼材料優化配置[J].振動與沖擊，2010，29(11)：156-159.

[9]郭中澤，陳裕澤.基于準則法的阻尼結構拓撲優化[J].宇航學報，2009，30(6)：2387-2391.

[10]李攀，鄭玲.SIMP插值的約束層阻尼結構拓撲優化[J].機械科學與技術，2014，33(8)：1122-1126.

[11]Xie Y M,Steven G P.Evolutionary structural optimization [M].Berlin,Heidelberg,New York:Springer,1997.

[12]戴德沛.阻尼技術的工程應用[M].北京：清華大學出版社，1991.

[13]梁新華.汽車車身薄壁件阻尼復合結構振動—聲學分析與優化[D].上海：上海交通大學，2007.

[14]Rao D.K.Frequency and loss factors of sandwich beams undervariousboundarycondition[J].Journalof Mechanical Engineering Science,1978,20:270-282.

[15]Sigmund O,Petersson J.Numerical instabilities in topology optimization:a survey on procedures dealing with checkerboard,mesh dependencies,local minima[J]. Strucaural Optimization,1998,16:68-75.

江西省自然科學基金（20122BAB216027）

學優化、精密驅動技術等研究。E-mail:hehonglin1967@163.com

中圖分類號：O422.6

文獻標識碼：A

DOI編碼：10.3969/j.issn.1006-1335.2016.01.004

文章編號：1006-1355(2016)01-0015-06

收稿日期：2015-08-14

基金項目：國家自然科學基金（51265040）；

作者簡介：賀紅林(1967-)，男，博士,教授，從事復雜結構動力

Topological Dynamic Optimization for Structure Vibration Reduction of Constraint Damping Plates Using EvolutionaryMethod

HE Hong-lin,TAOJie,YUAN Wei-dong,XIAO Zhi-yong

(Institute ofAeronautical Manufacturing,Nanchang HangKong University,Nanchang 330063,China)

Abstract:Structure topological optimization for vibration reduction of constraint damping plates was studied.The dynamic equations for the constraint damping plates were established,and a modal loss factor model for the plates was obtained. A topological optimization model to maximize the modal loss factor with lest viscoelastic damping materials consumption and minimum modal frequency variation as the constraints,was established for the constraint damping plates.The evolutionary structural optimization method was employed to solve the optimization model,and the modal loss factor sensitivity formula was deduced.Independent mesh filter method was introduced to avoid checkerboard appearance.An optimization program was accomplished for damping plate optimizing simulation.Results of simulation show that compared with the non-optimized method,the evolutionary structural optimization was more advantageous for realizing the viscoelastic material optimal layout, and the modal frequency variation was more stable.Harmonic response analysis was carried out for the damping plate to verify the topological optimization method,and the modal loss factor density index was introduced to evaluate the optimization performance.The results of the study show that the constraint damping plates can obtain better vibration suppression effects while the damping materials layout can maximize the modal loss factor.This method has strong practicability and high stability for the optimization design of damping structures.

Key words:vibration and wave;constraint damping plates;modal loss factor;checkerboard;dynamic optimization