TBM液壓管道等效固有頻率及穩定性研究

周井行，張懷亮,2，齊征宇

(1.中南大學 機電工程學院，長沙 410083；2.中南大學 高性能復雜制造國家重點實驗室，長沙 410083）

?

TBM液壓管道等效固有頻率及穩定性研究

周井行1，張懷亮1,2，齊征宇1

(1.中南大學 機電工程學院，長沙 410083；2.中南大學 高性能復雜制造國家重點實驗室，長沙 410083）

摘要：針對TBM掘進過程中產生的基礎振動對液壓長管道穩定性的影響，選取長管道相鄰兩固定支承及其之間的管道作為一個單元，建立基礎振動下管道單元的非線性微分方程，并通過實驗驗證振動微分方程的正確性，運用等價線性化推導出管道的等效固有頻率的數學模型。研究輸流管道系統固有頻率與穩定性的相關性，分別討論流體參數和結構參數對等效固有頻率的影響規律。結果表明：利用等效固有頻率能很好地反映系統的穩定性，兩者相關系數大于0.85。隨著流速、壓力及單元管長、內徑的增大或剛度、壁厚的減小，管道系統的等效固有頻率降低，系統穩定性降低；隨著基礎振動的增大，系統等效固有頻率越低，越容易失穩。

關鍵詞：振動與波；液壓管道；穩定性；基礎振動；等效固有頻率

硬巖掘進機(TBM)是專用于硬巖隧道掘進的專業化裝備[1]。因硬巖地質環境的影響，在其作業過程中不可避免地會產生強烈的振動[2]，強振動容易導致液壓管路不穩定，嚴重時甚至導致管道的破壞。因此，研究基礎振動下液壓管道的穩定性具有重要的工程意義。

國內外對管道穩定性的研究集中在無基礎振動下的管道臨界流速及臨界管長研究，如Paidoussis M P討論了輸流管道在定常流作用下失穩的振動特性[3]，Holmes P J證明了兩端固支管道在定常流作用下不會發生顫振失穩[4]。初飛雪研究了兩端支承管道流固耦合振動的穩定性[5]，推導了臨界流速和臨界壓力的解析表達式，然而上述均不考慮基礎振動對穩定性的影響。關于基礎振動作用下的管道研究主要集中在分岔及混沌方面，如鄒光勝研究了兩端固定輸流管在基礎簡諧激勵作用下的分岔及混沌運動[6]。包日東研究了基礎振動作用下管道出現混沌的參數條件和進入混沌的途徑[7]，雖然很多學者致力于基礎振動下管道的振動特性研究，但考慮基礎振動作用的管道穩定性問題鮮有人研究。

管道振動是一個典型的非線性問題，非線性問題線性化處理是非線性理論中的一種典型的近似解法。尤裕榮針對逆向卸荷式氣體減壓閥，采用線性化分析方法，對其工作穩定性進行分析[8]。章瑕璇將實際非線性振動系統等效為線性振動系統，并驗證了對非線性振動問題進行等效線性化的可行性，可見非線性問題線性化處理是一種有效的處理非線性問題的方法[9]。

本文以基礎振動作用下TBM管道單元為研究對象，在考慮非線性的情況下，建立其非線性微分方程，采用等價線性化法將非線性微分方程轉化為等價的線性方程，并通過實驗驗證方程的正確性，求得管道的等效固有頻率，通過對基礎振動下輸流管道固有頻率等于零所對應的基礎振動參數和系統進入分岔點所對應參數對比，得到了兩者的相關系數大于0.85，利用等效固有頻率能夠很好地反應系統的穩定性，利用控制變量的方法，分析單因素對等效固有頻率影響，分別研究了流體參數和結構參數對等效固有頻率的影響規律，具有一定的工程指導意義。

1　TBM輸流管道振動數學模型及等效固有頻率

TBM液壓長管道系統是由長管道及其固定支承組成，選取長管道相鄰兩固定支承及其之間管道作為長管道的一個單元，以管道單元為研究對象，理論模型如圖1所示。

圖1　管道理論模型

管道單元水平固定在基礎上，并且基礎也做簡諧運動，其運動方向垂直于管道軸線，即：W=Dsin(ωt)，其中D為激振幅值，ω為激振頻率。管道中流體以定常流速U流動，考慮了橫向彎曲時引起的附加非線性軸向力和管道材料的Kelvin-Voigt黏彈性，運用達朗伯原理和牛頓定理，得到基礎振動下輸流管道的非線性運動微分方程[10]

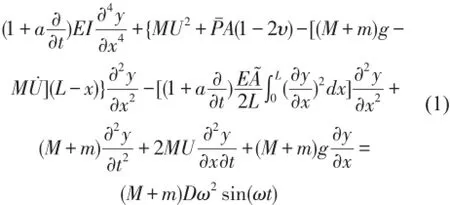
式中a為管道黏彈性系數，L為管道長度，U為管道內流體流速，M為單位長度流體質量，m為單位長度管道質量，EI為管道抗彎剛度，P為流體壓強，υ為泊松比，g為重力加速度，A?為管道有效橫截面積，A為管道過流截面積，t為時間。

引入如下無量綱參數

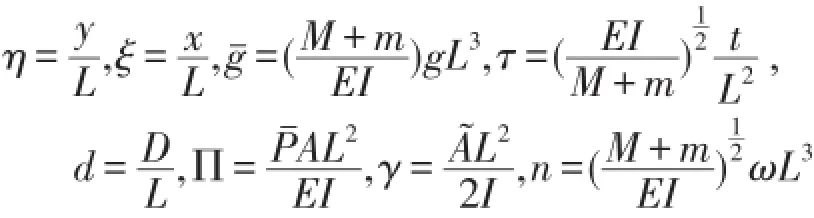
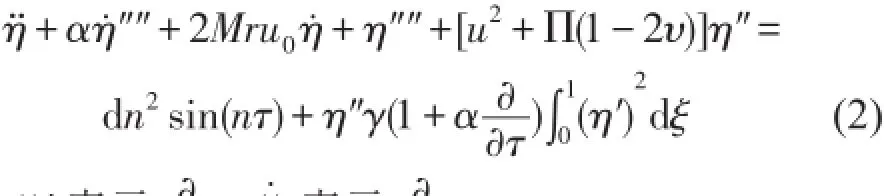
由于重力只影響振動平衡位置，對振動的其他特性無影響，所以忽略重力的影響后，并將上述無量綱參數代入式(1)中，得到基礎簡諧激勵作用下輸流管的無量綱運動微分方程

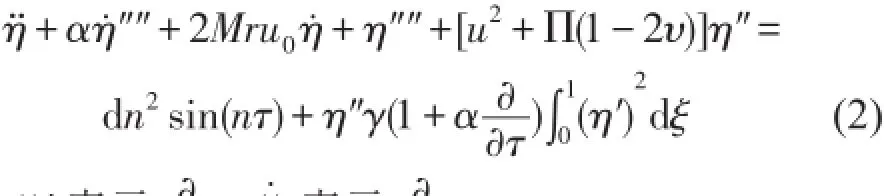
利用Galerkin方法對其進行離散化，令式中φr(r=1，2，…)用相同邊界條件下梁模型的模態函數來近似代替輸流管的模態函數，qr()τ為對應的廣義坐標。因為1階等價固有頻率最小，故取1階模態進行分析即可，取N=1。則Galerkin 1階展開式為將式(4)代入式(2)，在方程兩端同乘以φi()ξ并

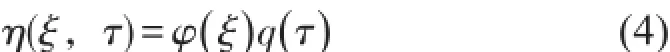
在[0，1]區間上積分，經過演繹可將方程式(2)化成式（5）其中

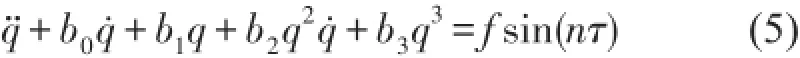
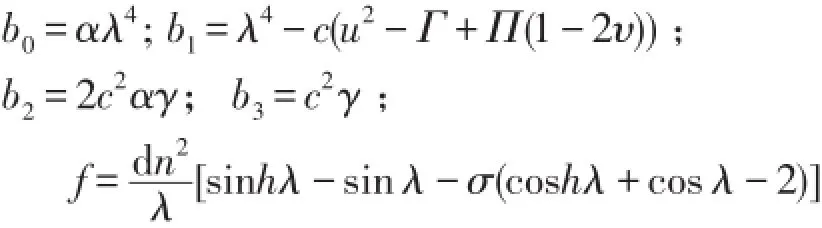
σ=(coshλ-cosλ)/(sinhλ-sinλ)

且λ=4.730 040 745，為兩端固定梁的第1階特征值。設非線性振動方程式(5)有以下的強迫振動解

式中A1為等價線性化振幅，β為相位差角。

將方程式(6)代入到方程(5)，經過復雜的數學推導，得到等價線性化振動方程

由等價線性化方程式(7)經計算可得等價固有頻率為

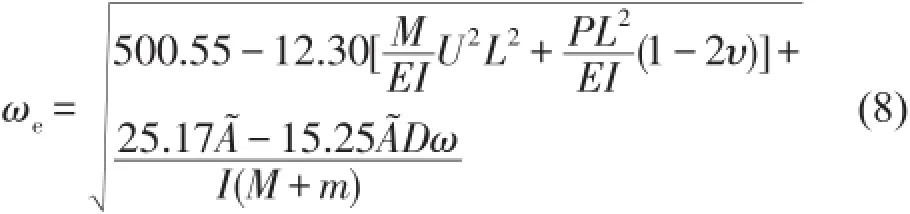
2　模型驗證

為驗證管道振動模型的正確性，結合課題組現有的實驗裝置，搭建實驗臺進行實驗驗證。

該實驗系統由動力缸液壓回路、加載缸液壓回路、液壓實驗臺控制系統、實驗管道系統、激振系統和振動信號監測及采集分析系統六部分組成，液壓直管道實驗系統原理如圖2所示。

圖2　液壓直管道實驗系統原理圖

取基礎振動幅值為0.002 mm，頻率為80 Hz，在相同基礎振動下，分析管道振動時域響應，將MATLAB中仿真計算結果與實驗測量結果進行對比，如圖3。分別對比仿真結果和實驗結果的響應頻率以及位移波峰平均值、波谷平均值，三者相對應的誤差分別為2.14%、7.72%、6.11%，處于允許范圍內，驗證數學模型的正確性。誤差一方面來源于仿真時忽略了軸向剪切力和外部阻尼等的影響，并且方程處理過程中的Galerkin離散化本身是一種近似，另一方面是由于實驗時數據采集和處理過程中產生的干擾和誤差。

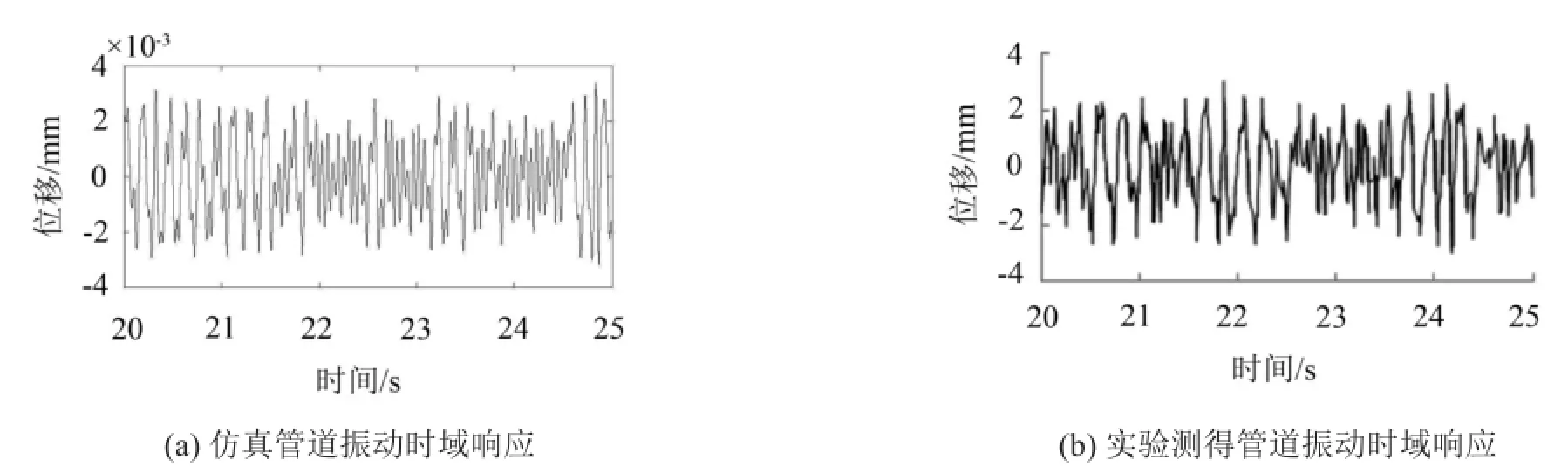
圖3　計算仿真與實驗結果對比

3　仿真分析

得到基礎振動下輸流管道的固有頻率后，為了研究基礎振動下輸流管道的穩定性，需要進一步確定等效固有頻率和系統穩定性的相關性，并分析輸流管道系統參數對固有頻率的影響規律，在MATLAB中對輸流管道系統進行仿真分析，其中系統參數包括流體參數（速度、壓力）和結構參數（固支長度、彎曲剛度、內徑、壁厚），設定仿真參數如下：管道固支支承長度L=1 m，彈性模量E=2.11×105MPa，管道內徑為d=0.038 m，管道壁厚為 δ=0.003 m ，管截面流體流動面積A=1.134×10-3m2，管道慣性截面矩I=8.163×10-9m4，油液密度ρ液=890 kg/m3，管道密度ρ管=7 800 kg/m3，單位長度管道質量m=3.014 kg，單位長度油液質量M=1.009 kg，泊松比為 υ=0.29。流速為 U=1.0 m/s，壓力為P=10 MPa，基礎振動的幅值及頻率分別取：D=0.005 m、ω=10 Hz、D=0.010 m、ω=75 Hz、D=0.015 m、ω=100 Hz。在分析時，當某個參數為影響參數時，取其為變化值，其余值取定值。

3.1輸流管道的等效固有頻率與穩定性的相關性研究

由于TBM實際工況中基礎振動的影響不能忽略，因此在推導出在考慮基礎振動的等效1階固有頻率模型后，基于等效固有頻率對管道系統的穩定性進行分析之前，首先需要確定等效固有頻率與分岔失穩點的關系，從而推導出輸流管道穩定性與等效固有頻率的相關性。

由文獻[11]可知，在無基礎振動下，兩端固支輸流管道在系統1階固有頻率大于零時，系統不會發生分岔，處于穩定狀態；當系統的1階固有頻率等于零時為分岔的臨界點。參考文獻[12]基于仿真參數，先取不同基礎振動幅值，以基礎振動頻率為分岔參數做分岔圖，得到不同分岔點所對應的基礎振動頻率及幅值，如圖4所示

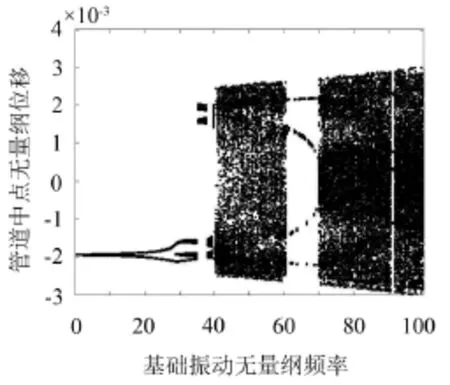
圖4　無量綱振幅為0.002下以頻率為參數的分岔圖

通過這種方法，以基礎振動頻率為橫坐標，以振幅為縱坐標，建立坐標系，找出多個分岔點坐標，如根據圖4即可得到一個分岔點坐標（40，0.002），將分岔點標入到坐標系中，并用光滑曲線將之連接起來，得到不同基礎振動下系統出現分岔時所對應的基礎振動頻率和幅值圖，如圖5所示。

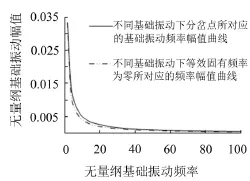
圖5　管道分岔點的無量綱基礎振動頻率幅值

取仿真參數，并對參數進行無量綱化，利用等效固有頻率式（8）計算出不同基礎振動下等效固有頻率ωe=0的點所對應的基礎振動頻率及幅值，并將所有對應的點標注到圖5中，如圖5所示。

從圖5中可以看出，兩者所對應的趨勢是一致的，但是，等效固有頻率等于零所對應的基礎振動頻率幅值要比分岔點所對應的基礎振動頻率幅值小，這是因為截斷誤差所致，等效固有頻率是基于單模態，而做分岔圖時是基于雙模態，這與文獻[8]中得出的結論是一致的，即單模態系統的臨界值要小于雙模態系統的臨界值。經計算，其相關性系數大于0.85，因此利用等效固有頻率大于等于零可以很好的描述分岔圖中分岔點及其之前的運動。

3.2流體參數對等效固有頻率的影響

3.2.1流速對等效固有頻率的影響規律

油液的流速U是管道系統流體參數中非常重要的一個因素，已有研究表明，管道的振動通常是由于流速過大而引起的，當流體流速超過某個臨界值的時候，管道就會發生失穩而出現分岔，然而在基礎振動作用下，會加劇流速對管道的影響。取流速為變化值，取管道長度L=1 m，并取三組不同的如上所述基礎振動，來探索在此振動下，流速對等效固有頻率的影響規律。

圖6所示為基礎振動作用下，輸流管道的等效固有頻率隨流體流速的變化規律。由圖6可以看出，等效固有頻率隨流體流速的增加而顯著下降，其下降的趨勢為先緩慢下降，隨著流速增大，其下降的速度越快，且當等效固有頻率等于零時，對應的流速為管道的臨界流速即管道出現失穩從而發生分岔的點。固定管長為L=1 m，改變基礎振動，經計算當基礎振動幅值為0.005 m，頻率為10 Hz時，所對應的臨界流速值為6 m/s；當基礎振動幅值為0.01 m，頻率為75 Hz時，所對應的臨界流速值為4.3 m/s；當基礎振動幅值為0.015 m，頻率為100 Hz時，所對應的臨界流速值為2.8 m/s。說明隨著基礎振動頻率和幅值的增大，其他參數一定的情況下，系統振動發生分岔的臨界流速值逐漸減小，而且等效固有頻率也會相應減小。

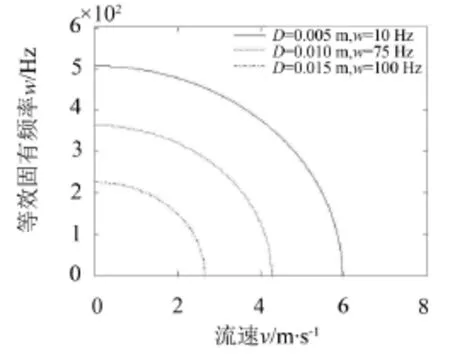
圖6　基礎振動作用下等效固有頻率隨流速的變化

3.2.2壓力對等效固有頻率的影響規律

管道中流體的壓力P是管道系統流體參數中非常重要的一個因素，執行機構如液壓缸的動作是通過流體的壓力使其運動的。設定壓力值范圍為0～100 MPa，取不同的基礎振動參數，其他參數不變。

圖7所示為基礎振動作用下等效固有頻率隨著壓力的變化曲線。隨著壓力的增大，等效固有頻率大幅下降，直到等效固有頻率為零時，所對應的壓力為臨界壓力值即管道振動出現失穩而發生分岔的油液壓力值。從圖中可以看出，發生分岔的臨界壓力是比較大，通常液壓管道中的壓力在20 Mpa以上，因此，流體的壓力對管道的振動影響相對較小。

圖7　基礎振動作用下等效固有頻率隨壓力的變化

3.3結構參數對等效固有頻率的影響

3.3.1單元管長對等效固有頻率的影響規律

設定管道長度范圍為0～4 m，其他參數取定值。圖8所示為不同基礎振動作用下，等效固有頻率隨管道單元長度變化曲線。隨著固支長度的增加，等效固有頻率下降，直到等效固有頻率為零時，所對應的管道長度即為管道的臨界固支長度。經計算可以得到：基礎振動幅值為0.005 m，頻率為10 Hz時，所對應的臨界管道長度值為2.5 m；當基礎振動幅值為0.01 m，頻率為75 Hz時，所對應的臨界管道長度為1.66 m；當基礎振動幅值為0.015 m，頻率為100 Hz時，所對應的臨界管道長度值為0.98 m，隨著基礎振動頻率和幅值的增大，臨界管道長度減小，且隨著振動幅值和頻率的增大，等效固有頻率相應減小。因此，減小單位固支管道的長度有利于提高管道系統的穩定性。

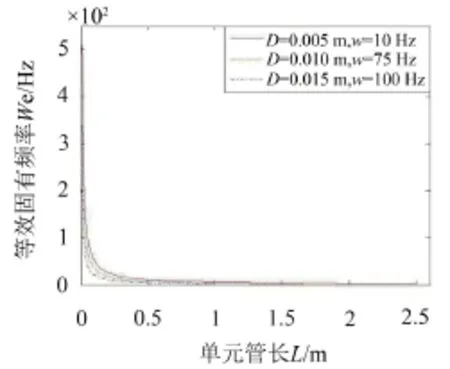
圖8　基礎振動下等效固有頻率隨單元管長變化

3.3.2彎曲剛度對等效固有頻率的影響規律

剛度反應物體抵抗變形的能力，是材料彈性變形難易程度的一個象征。本文描述的彎曲剛度為彈性模量與管截面慣性矩之間的乘積。保持其他參數不變，只改變管道的剛度觀察等效固有頻率的變化。

如圖9所示，當管道剛度從0增加到2 500 N/m時，等效固有頻率首先急劇增加，之后趨于平緩。從圖中可以看出，當剛度較小時，增大剛度能顯著的提高系統的等效固有頻率，有利于抑制系統的振動，但是，當剛度增大到一定程度時，等效固有頻率將不再增大。而隨著基礎振動的增大，在相同參數條件下，等效固有頻率隨著基礎振動的增大而相應減小，說明基礎振動使管道更容易產生振動。因此，為了減小管道振動，需要增大管道的彎曲剛度即通過選用不同的材料來改變彈性模量的值從而增加剛度。

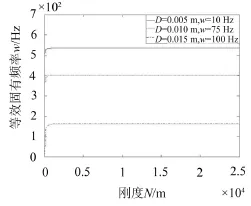
圖9　彎曲剛度對等效固有頻率的影響

3.3.3內徑對等效固有頻率的影響規律

管道內徑的大小對管道的穩定性能有一定影響，其他參數不變，且管道壁厚為0.003 m時，只改變管道內徑觀察其對等效固有頻率的影響規律，并通過改變基礎振動幅值及頻率，觀察基礎振動對內徑及等效固有頻率的影響規律。

如圖10所示，隨著內徑的增大等效固有頻率降低，降低的趨勢是先急劇下降，然后下降趨勢逐漸平緩，直至等效固有頻率等于零，此時管道出現分岔發生失穩，因此，管道壁厚不變的情況下，內徑越大越容易出現分岔，從而失穩。而隨著基礎振動的增大，發生分岔的管道臨界內徑值會相應變小，基礎振動會加強管道振動，因此在基礎振動較大的情況下，且壁厚一定的情況下，應該選用內徑較小的管道，以減小管道失穩的可能性。

3.3.4壁厚對等效固有頻率的影響規律

其它參數不變，管道內徑為0.019 m時，只改變管道壁厚，觀察壁厚對等效固有頻率的影響規律。

如圖11所示，當管道壁厚由0增大到0.05 m時，等效固有頻率與壁厚呈線性遞增關系，壁厚越厚，等效固有頻率隨著變大，所以適當增加壁厚有助于提高管道振動的等效固有頻率。從圖中還可以得到，隨著基礎振動的增大，等效固有頻率隨壁厚遞增的斜率會變小。說明基礎振動會使管道穩定性降低，因此，增大壁厚有利于提高等效固有頻率，管道穩定

性也會提高，從而可以很好的避免分岔的出現，有助于減小管道振動。

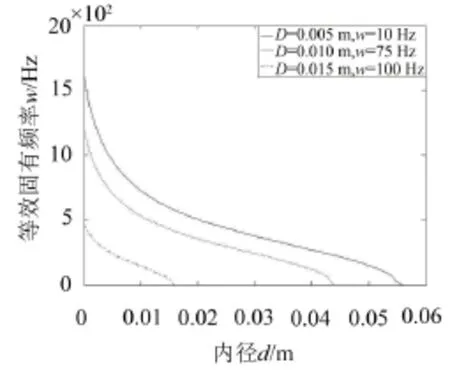
圖10　內徑變化對管道等效固有頻率的影響

圖11　壁厚對管道等效固有頻率的影響

4　結　語

（1）建立基礎振動作用下管道的非線性偏微分方程，通過實驗驗證了方程的正確性，利用等價線性化法推導出等效固有頻率數學模型；

（2）等效固有頻率等于零所對應的基礎振動參數即為管道發生失穩而分岔時所對應的基礎振動參數，兩者的相關性系數大于0.85，利用等效固有頻率能夠很好的反應輸流管道系統的穩定性；

（3）隨著流速、壓力及單元管長、內徑的增大和剛度、壁厚的減小，管道系統的等效固有頻率降低，系統穩定性降低；隨著基礎振動的增大，系統等效固有頻率越低，分岔點所對應的流速、壓力、管長、內徑值越小，越容易失穩。

參考文獻：

[1]陳立和.淺析機械應用中的TBM與液壓系統[J].吉林省教育學院學報，2011，27(2)：138-139.

[2]陳炳瑞，馮夏庭，曾雄輝.深埋隧洞TBM掘進微震實時監測與特征分析[J].巖石力學與工程學報，2011，30(2)：275-283.

[3]Pa?doussis M P,Sarkar A,Semler C.A horizontal fluidconveying cantilever:spatial coherent structures,beam modes and jumps in stability diagram[J].Journal of Sound and Vibration,2005,280(1):141-157.

[4]Holmes P J.Pipes supported at both ends cannot flutter[J]. Journal ofApplied Mechanics,1978,45(3):619-622.

[5]初飛雪.兩端簡支輸液管道流固耦合振動分析[J].中國機械工程，2006，17(3)：248-250.

[6]鄒光勝，金基鐸，聞邦椿.Melnikov方法在輸流管混沌運動研究中的應用[J].力學與實踐，2004，26(2)：29-32.

[7]包日東，金志浩，聞邦椿.一般支承條件下輸流管道的非線性動力學特性研究[J].振動與沖擊，2009，28(7)：153-157.

[8]尤裕榮，曾維亮.氣體減壓閥的穩定性分析[J].火箭推進，2009，35(5)：34-39.

[9]章瑕璇，唐云冰.非線性振動問題等效線性化研究[J].振動工程學報，2004，17(22)：918-920.

[10]ZouGuangsheng,JinJIduo.Stabilityandchaotic vibrations of a pipe conveying fluid under harmonic excitation[J].Journal of Shanghai University,2000,4(3): 179-185.

[11]趙鳳群，王忠民.具有可移動彈性支承輸流管道的穩定性分析[J].機械工程學報，2004，40(9)：38-41.

[12]齊征宇，張懷亮，彭歡.TBM液壓直管道的非線性動力學特性研究[J].噪聲與振動控制，2014，34(3)：61-66.

向：液壓元件動力學行為。

E-mail:zhoujingxing@csu.edu.cn

E-mail:csu2001zhl@163.com

中圖分類號：O353

文獻標志碼：A

DOI編碼：10.3969/j.issn.1006-1335.2016.01.007

文章編號：1006-1355(2016)01-0032-06

收稿日期：2015-06-23

基金項目：國家“973”重點基礎研究發展計劃資助項目(2013CB035400)

作者簡介：周井行（1990-），男，湖南婁底人，碩士生，研究方

通訊作者：張懷亮，男，教授，博士生導師

Study on the Equivalent Natural Frequencies and Stability
of TBM Hydraulic Pipelines

ZHOU Jing-xing1,ZHANG Huai-liang1,2,QI Zheng-yu1

(1.College of Mechanical and Electrical Engineering,Central South University, Changsha 410083,China; 2.State Key Laboratory of High Performance and Complex Manufacturing,Central South University, Changsha 410083,China)

Abstract:The impact of foundation vibration generated in TBM tunneling on the stability of long hydraulic pipelines was studied.Selecting the pipe segment with two neighboring supports as an element,the nonlinear differential equation of the pipeline unit in the foundation vibration condition was established,and the validity of the differential equation was verified through experiments.Equivalent linearization technique was applied to obtain the mathematical model for analyzing the pipeline’s equivalent inherent frequency.The relevance between inherent frequency and stability of fluid-flow in the pipeline was analyzed,and the effects of fluid parameters and structural parameters on the equivalent inherent frequency were discussed.The results indicate that the equivalent inherent frequency can reflect the stability of system very well and the correlation coefficient is greater than 0.85.The equivalent inherent frequency and stability decrease with the increase of the flow velocity,pressure,the length and internal diameter of the pipeline unit as well as the decrease of the rigidity and wall thickness of the pipeline unit.As the foundation vibration increases,the equivalent inherent frequency of the system will decrease,and the system may lose its stability more easily.

Key words:vibration and wave;hydraulic pipeline;stability;foundation vibration;equivalent natural frequency