Extremal Values on Distance-Degree-Based Topological Indices of Cacti with r Cycles

WANG Yu-xi, CHEN Han-lin, DENG Han-yuan

(College of Mathematics and Computer Science, Hunan Normal University, Changsha 410081, China)

?

Extremal Values on Distance-Degree-Based Topological Indices of Cacti with r Cycles

WANG Yu-xi, CHEN Han-lin, DENG Han-yuan

(College of Mathematics and Computer Science, Hunan Normal University, Changsha 410081, China)

Keywordscactus;thedegreedistanceindex;theGutmanindex;theadditivelyweightedHararyindex;themultiplicativelyweightedHararyindex;extremalvalue

In this paper, we will consider the degree distance index [4,6,19], the Gutman index [2,12], the additively weighted Harary index [1] and the multiplicatively weighted Harary index [17]. They are defined for a connected graphGas follows, repectively

WewilldeterminethemaximalvaluesoftheadditivelyweightedHararyindex,themultiplicativelyweightedHararyindexandtheminimalvalueofthedegreedistanceindex,theGutmanindexamongallcactiofordernwithrcycles,andcharacterizethecorrespondingextremalgraphs.

1Preliminaries

For a graphG, the first Zagreb indexM1(G) and the second Zagreb indexM2(G) ofGare, respectively

ThefirstZagrebcoindexandthesecondZagrebcoindexofGare,respectively

WenowintroducethefollowingnewinvariantsforanygraphG

NotethatM*(G)=2M2(G)-M1(G), N*(G)=M1(G)+M2(G).

Beforestatingourmainresults,wewilllistsomelemmasaspreliminaries,whichwillplayanimportantroleinthenextproofs.

IfG∈G(n,r), thenm=|E(G)|=n+r-1. The following lemma is obtained from Propositions 2 and 4 in [3].

Lemma1[3]IfG∈G(n,r),n≥2, then

Lemma 2(i) LetG∈G(n,r)withlargestM1(G).ThenthemaximumdegreeΔ(G)=n-1.

(iii)LetG∈G(n,r)withlargestN*(G).ThenΔ(G)=n-1.

2Main results

Inthissection,wewillcharacterizethemaximalgraphswithrespecttothemaximalvaluesoftheadditivelyweightedHararyindex,themultiplicativelyweightedHararyindexandtheminimalgraphwithrespecttothedegreedistanceindex,theGutmanindexamongallcactiofordernwithrcycles.

Theorem 3LetG∈G(n,r).Then

(i) M1(G)≤n2-n+6rwithequalityifandonlyifG?G0(n,r).

(iii) N*(G)≤2n2+2nr-3n+8r+1withequalityifandonlyifG?G0(n,r).

Now,westudythemaximalvaluesoftheadditivelyweightedHararyindex,themultiplicativelyweightedHararyindexandtheminimalvalueofthedegreedistanceindex,theGutmanindexamongallcactiofordernwithrcycles.

ProofBythedefinitionofHA,wehave

with equality if and only ifG?G0(n,r).

Theorem5IfG∈G(n,r), thenDD(G)≥(3n+4r- 4)(n-1)-6rwith equality if and only ifG?G0(n,r).

ProofBythedefinitionoftheDDindex,wehave

M1(G)+4(n+r-1)(n-1)-2M1(G) (by Lemma 1(1))=

4(n+r-1)(n-1)+M1(G)≥

(3n+4r-4)(n-1)-6r(by Theorem 3(i))

with equality if and only ifG?G0(n,r).

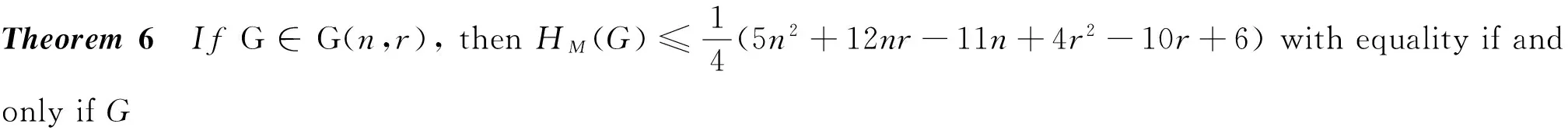
ProofBythedefinitionofHM,wehave

Theorem7IfG∈G(n,r), then Gut(G)≥2n2+6nr-5n-4r2-16r+3 with equality if and only ifG?G0(n,r).

ProofBythedefinitionoftheGutmanindex,wehave

M2(G)+4(n+r-1)2-2M2(G)-M1(G) (by Lemma 1(2))=

4(n+r-1)2-(M1(G)+M2(G))=

4(n+r-1)2-N*(G) (by the difinition ofN*(G))≥

2n2+6nr-5n+4r2-16r+3 (by Theorem 3(iii))

with equality if and only ifG?G0(n,r).

By selectingr=0 orr=1 in Theorems 4-7, we can get the following results.

Corollary8Amongalltreesofordern,

(ii)theuniquetreewiththeminimaldegreedistanceindexDDisthestarSn,andDD(Sn)=3n2-7n+4[15];

(iv)theuniquetreewiththeminimalGutmanindexGutisthestarSn,andGut(Sn)=2n2-5n+3[2].

Corollary9Amongallunicyclegraphsofordern,

References:

[1]ALIZADEH Y, IRANMANESH A, DOT. Additively weighted Harary index of some composite graphs [J]. Discr Appl Math, 2013,313(1):26-34.

[2]ANDOVA V, DIMITROV D, FINK J,etal. Bounds on Gutman index [J]. Commun Math Comput Chem, 2012,67(2):515-524.

[5]CHEN S B, LIU W J. Extremal modified Schultz index of bicyclic graphs [J]. Commun Math Comput Chem, 2010,64(3):767-782.

[6]DANKELMANN P, GUTMAN I, MUKWEMBI S,etal. On the degree distance of a Graph [J].Discr Appl Math, 2009,157(13):2773-2777.

[7]DANKELMANN P, GUTMAN I, MUKWEMBI S,etal. The edge-Wiener index of a graph [J].Discr Appl Math, 2009,309(10):3452-3457.

[8]DENG H, KRISHNAKUMARI B, VENKATAKRISHNAN Y,etal. Multiplicatively weighted Harary index of graphs [J]. J Comb Optim, 2013，30(4)：1125-1137.

[10]DOBRYNIN A A, KOCHETOVA A A. Degree distance of a graph: a degree analogue of the Wiener index [J]. J Chem Inf Comput Sci, 1994,34(5):1082-1086.

[11]FENG L. The Gutman index of unicyclic graphs [J]. Discr Math Algo Appl, 2012,4(3):31-39.

[12]FENG L, LIU W. The maximal Gutman index of bicyclic graphs [J]. Commun Math Comput Chem, 2011,66(2):699-708.

[13]GUTMAN I. Selected properties of the Schultz molecular topological index [J]. J Chem Inf Comput Sci, 1994,34(5):1087-1089.

[14]HUA H, ZHANG S. On the reciprocal degree distance of graphs [J]. Discr Appl Math, 2012,160(7-8):1152-1163.

[16]IVANCIUC O, BALABAN T S, BALABAN A T,etal. Reciprocal distance matrix, related local vertex invariants and topological indices [J]. J Math Chem, 1993,12(1):309-318.

[17]LI S, ZHANG H. Some extremal properties of the multiplicatively weighted Harary index of a graph [J]. J Comb Optim, 2014,31(3):1-8.

[19]TOMESCU I. Some extremal properties of the degree distance of a graph[J]. Discr Appl Math, 1999,98(1-2):159-163.

[20]TOMESCU I. Unicyclic and bicyclic graphs having minimum degree distance [J]. Discr Appl Math, 2008,156(1):125-130.

[21]XU K, DAS K C, BALACHANDRAN S. Maximizing the Zagreb indices of (n,m)-graphs [J]. Commun Math Comput Chem， 2014,72(3):641-654.

[22]XU K, DAS K C, KLAV?AR S,etal. Extremal (n,m)-graphs with respect to distance-degreebased topological indices [J]. Commun Math Comput Chem, 2014,72(3):865-880.

[23]XU K, LIU M, DAS K C,etal. A survey on graphs extremal with respect to distance based topological indices [J]. Commun Math Comput Chem, 2014,71(3):461-508.

[24]ZHONG L, XU K. Inequalities between vertex-degree-based topological indices [J]. Commun Math Comput Chem, 2014,71(3):627-642.

(編輯HWJ)

DOI:10.7612/j.issn.1000-2537.2016.04.013

收稿日期：2015-07-31

基金項目：國家自然科學 項目(61572190)；湖南省研究生創(chuàng)新 項目(CX2015B162)

*通訊作者,E-mail：hydeng@hunnu.edu.cn

中圖分類號O157.5

文獻標識碼A

文章編號1000-2537(2016)04-0078-06

具有r個圈的仙人掌圖關于距離-度指數(shù)的極值

王雨溪，陳翰麟，鄧漢元*

(湖南師范大學數(shù)學與計算機科學學院，中國 長沙410081)

摘要設G=(V，E)是一個連通圖.G的基于距離-度的拓撲指數(shù)一般定義為(u,v))，其中F=F(x,y,z)是一個函數(shù),deg(u)是頂點u的度,d(u,v)是u和v之間的距離.若F分別是(x+y)z,xyz,(x+y)z-1和xyz-1，則IF(G)就分別是距離指數(shù)DD(G),Gutman指數(shù)Gut(G)，和加權Harary指數(shù)HA(G)與積加權Harary指數(shù)HM(G).本文確定了具有r個圈的仙人掌圖關于和加權Harary指數(shù)與積加權Harary指數(shù)的最大值，以及關于度距離指數(shù)與Gutman指數(shù)的最小值；并刻畫了對應的極圖.

關鍵詞仙人掌圖；度距離指數(shù)；Gutman指數(shù)；和加權Harary指數(shù)；積加權Harary指數(shù)；極值