基于ANSYS的響應曲面優化在船舶甲板支柱線性屈曲分析中的應用

黃 技，呂鴻冠，嚴 謹，葉劍釗

（廣東海洋大學 工程學院，廣東湛江 524088）

基于ANSYS的響應曲面優化在船舶甲板支柱線性屈曲分析中的應用

黃 技，呂鴻冠，嚴 謹，葉劍釗

（廣東海洋大學 工程學院，廣東湛江 524088）

隨著有限元技術和計算機軟硬件的迅速發展，結構優化設計的理論和算法均得到巨大的飛躍，并越來越受到工程師的重視。利用ANSYS的Static Structural模塊和Design Exploration模塊，在考慮壓桿穩定的情況下，對船舶甲板支柱進行線性屈曲分析，得到一階線性屈曲因子后，對其進行結構優化，通過對優化數據的分析對比，得到支柱結構的最優化方案，在現實工程應用中具有一定的指導意義。

結構優化設計；線性屈曲；壓桿穩定；船舶支柱

0 引言

優化設計的概念起源于人們的社會生產實踐活動。當一個產品設計或一項工程結構不能滿足實際需求時，設計師或工程師往往會依照前人或自己累積的經驗，遵循一定的“優化思想”和“優化原則”，通過采用不同的方法，不斷改變設計模型和設計變量，從而改善產品或結構的各項性能指標，使設計達到最優化。

本文通過ANSYS的Static Structural模塊，在考慮壓桿穩定的情況下，對船舶甲板支柱進行線性屈曲分析，得到一階線性屈曲因子后，利用一階性線性屈曲因子與特征值（預應力）的關系，求出屈曲極限，并在Design Exploration模塊中的Response Surface對支柱進行結構優化，通過對設計變量和目標函數的分析對比，得到支柱結構的最優化方案，在現實工程應用中具有一定的指導意義。

1 優化理論

1.1 結構優化的數學模型

1.1.1 設計變量

對一個工程結構進行優化設計，首先應根據與性能指標密切相關的基本設計參數對結構進行數學建模。在數學模型中，部分設計參數是動態的，需要在優化方程中求解。在這部分參數中，線性獨立的設計參數稱為“設計變量”。結構優化的目的就是要在滿足預先指定的限制條件（約束函數）中，尋找設計變量的最優解。

1.1.2 目標函數

在對結構進行優化設計過程中，至少有一個衡量優化結果優劣的函數，稱為目標函數。除了目標函數外，還有對結構性能和設計指標進行限制的約束函數，保證結構設計在合理范圍內。如果優化設計只有單個目標函數，稱為單目標優化，如果目標函數不止一個，稱為多目標優化。單目標結構優化設計的數學模型如下［1］：

尋找一組設計變量：

使目標函數：

且滿足約束條件：

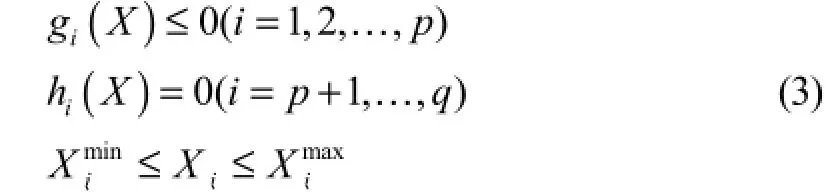
式中：F（X）稱為目標函數；gi（X）稱為不等式約束函數；hi（X）稱為等式約束函數；X稱為設計變量列向量；稱為設計變量Xj取值的下限和上限。

如果X=［X1X2X3… Xn］T滿足所有約束條件，則稱其為可行解或可行點，所有可行點組成的集合稱為可行域。使目標函數值最小（或最大）的可行解即為最優解。

1.2 屈曲分析理論

設結構的應力剛度矩陣［S］是基于膜應力的任意基準強度。在線性條件下，［S］和通常的剛度矩陣［K］為位移的函數。如果基準條件下的位移矩陣｛D｝加上虛位移矩陣｛φ｝，而作用的載荷［F］保持不變，那么為了使狀態｛D｝和｛D+φ｝保持平衡，必須滿足：

式中，［K］為剛度矩陣；［S］為應力剛度矩陣；｛φ｝為虛位移矩陣；λ為特征值（也成為比例因子或載荷因子）。虛位移矩陣｛φ｝代表模型的屈曲形狀，也稱為屈曲模態。在通常的屈曲分析中，一般只對結構的第一個特征值和特征矢量感興趣。由于特征值不考慮任何非線性和初始擾動，所以它只是一種理想解。

2 優化模型與方案

本文采用的優化模型是無人的非自航的箱形駁船的甲板支柱［2］，根據中國船級社2012年《鋼質海船入級與建造規范》的要求進行計算后，得出甲板支柱最大受力為598kN。在這里，選擇受力最大的情況，即598kN作為約束條件。則所用鋼管的受力極限必須滿足式（7）。

通過查詢國標無縫鋼管規格表，在這里選擇Φ219×15規格的無縫鋼管作為起始的船舶支柱材料。接下來，先通過ANSYS的Geometry模塊建立鋼管的幾何模型，將模型導入Static Structural模塊求解，得到一階屈曲因子，根據一階屈曲因子判斷所選材料的屈曲極限是否滿足式（7），若不滿足，重新選擇鋼管規格，重復上述步驟；若滿足，則用Design Exploration模塊進行優化，從而得到最經濟實用的結構設計方案。整個過程的流程如下：

1）通過ANSYS Static Structural進行結構靜力學分析；

2）根據一階屈曲因子判斷Fs≥598kN是否成立；若成立，進入3）；不成立，重新選擇鋼管型號重復1）；

3）設置優化變量，進入Design Exploration進行優化；

4）分析對比優化結構，選擇最優方案；

5）利用新的型號計算屈曲極限，查看是否滿足要求。

3 ANSYS結構靜力學分析

3.1 前處理及預應力分析

利用ANSYS的Geometry模塊對Φ219×15規格的無縫鋼管進行幾何建模，模型的材料為默認的Stainless Steel（不銹鋼）。建模過程中，將內徑設為優化參數 P5-Inner Diameter。將建好的模型導入Static Structural模塊的Mesh進行網格劃分，將網格大小設置為0.01m。網格劃分完畢后，共有30124 個Nodes（節點），4564個Elements（有限單元）。

將甲板支柱的工作狀態抽象為一端為固定約束，另一端是自由端的力學模型。在這里，把鋼管底面添加Fix Support（固定端約束），鋼管的頂面施加1000N的Force（預應力），并將幾何體的Mass（重量）設為優化參數P2-Solid Mass，結果如圖1和圖2所示。設置好其他參數后，對模型進行預應力分析，分析結果如圖3和圖4所示。

圖1 固定端約束

圖2 預應力的大小和方向

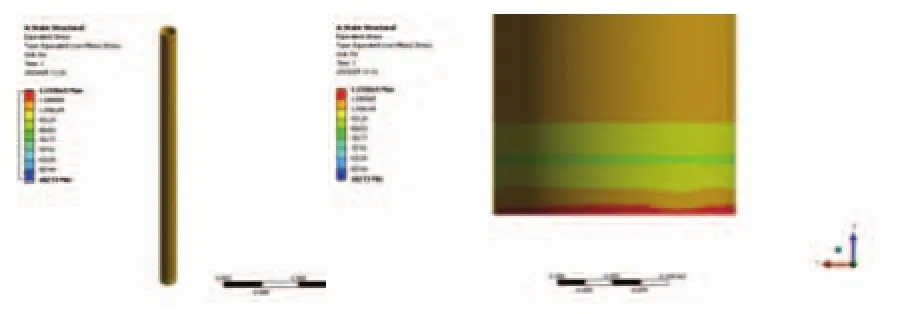
圖3 1 000N預應力下的應力分布云圖

圖4 1 000N預應力下的應變分布云圖

從上面的結果可以看出，應力主要集中在鋼管底部，而總應變主要集中在鋼管頂部，且總應變非常小，最大總應變只有2.08×10-6m。上述分析結果是在預應力為1 000N的情況下求解出來的，不具備實際的工程應用價值。

3.2 線性屈曲分析

通過上面的分析可以看出，根據式（6），只要能求出鋼管的一階屈曲因子，便可計算鋼管的屈曲極限。將Static Structural模塊與Linear Buckling模塊進行數據關聯，設置屈曲模態為六階模態進行求解，求解后的屈曲因子如表1所示。

表1 不同模態的屈曲因子

從表1可以看出，一階與二階，三階與四階，五階與六階對應的屈曲因子幾乎相同，故這里只取第一、三、五階進行分析。通過模態云圖（圖 5、圖6、圖7），可以直觀地看出不同模態下鋼管的變形情況。

圖5 一階屈曲分析結果

圖6 三階屈曲分析結果

圖7 五階屈曲分析結果

從上面不同階的分析結果可以看出，模態階級越大，變形越大，根據前面理論部分的分析可知，只需關注第一階的分析結果即可。通過表1可知，一階線性屈曲因子為1 548.3，則在式（6）中：

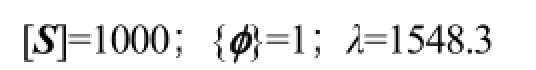
將上述三個數值代入式（6），可求得：

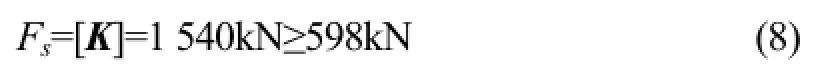
故所選的無縫鋼管Φ219×15符合結果要求。且1 540kN/598kN=2.58，說明結構仍具有很大的優化空間。這里，一階屈曲因子設為優化參數 P3-Total Deformation Load Multiplier。

4 結構優化

4.1 優化方案

根據上面的結果，可知Φ219×15規格的無縫鋼管的屈曲極限1 540kN完全滿足實際需要，且對于598kN來說仍有很大的優化空間。船舶甲板支柱在工作狀態下是受壓的二力桿，根據材料力學理論［4］，提高壓桿穩定性措施主要有：1）選擇合理的截面形狀；2）改變壓桿的約束條件；3）合理選擇材料。

顯然，對于船舶甲板支柱的優化，只能通過改變截面來進行。在這里，選擇對壁厚進行優化設計。對壁厚進行優化，其本質上是改變橫截面的表面積，在保證屈曲極限不低于598kN的情況下，使結構質量減輕，得到最優化方案。優化參數經過整理分析后如表2所示。

表2 優化參數類型

4.2 優化結果

進入ANSYS的Design Exploration模塊，將設計變量P5-Inner Diameter的范圍設置為179～199，得到的設計點參數如表3所示。

做好其它相關設置后，開始進行優化分析。分析結果如圖8和圖9所示。

從圖8可以看出，結構質量隨著內徑的增加呈線性遞減的趨勢。從圖9可以看出，Design Point 3在所有設計點中內徑是最大的，且質量也是最小的，故Design Point 3是理想的方案。通過分析結果可知Design Point 3的參數和未優化前的參數對比如表4所示。

圖8 質量與內徑的關系

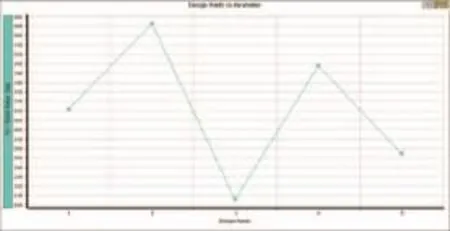
圖9 不同設計點的質量分布

表4 優化前后的對比

通過圖10和圖11的Spider圖，可以清晰地看出優化前后兩者的區別。

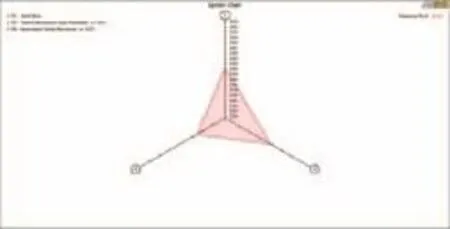
圖10 優化前的Spider圖

圖11 優化后的Spider圖

從圖10和圖11可以看出，優化后雖然應力相對優化前大大增加，但是總質量和一階屈曲因子也隨之下降，下面通過計算來驗證優化方案是否可行。根據上面分析的結果，可知：

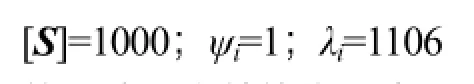
將上述三個數值代入式（6），可求得：

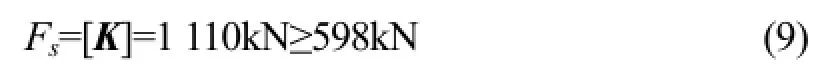
滿足Fs≥598kN。優化后的總質量206.17kg，優化前的總質量301.86kg，則：

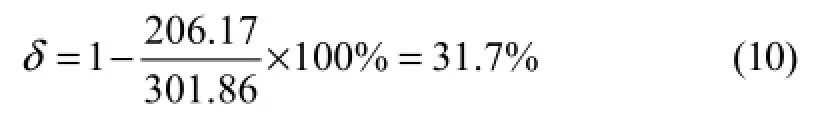
式中，δ是材料節約比率。

從上述分析可以看出，結構優化后，屈曲極限仍滿足工程需求，且總質量只有優化前的68.3%，大大降低了工程成本。

5 結論

本文以結構優化理論和屈曲分析理論為基礎，建立船舶甲板支柱的結構優化模型，通過ANSYS Static Structural模塊和Design Exploration模塊對甲板支柱結構進行優化。優化結果表明，在滿足屈曲極限大于極限工作應力的前提下，支柱壁厚減少了10mm，結構質量只有原來的68.5%，極大降低了成本，在現實應用中具有一定的參考價值。

［1］ 王棟. 結構優化設計-探索與進展［M］. 北京：國防工業出版社， 2013.

［2］ 黃志新， 劉成柱. ANSYS Workbench 14.0超級學習手冊［M］. 北京： 人民郵電出版社， 2013.

［3］ 黃志新， 劉成柱. ANSYS Workbench 14.0超級學習手冊［M］. 北京： 人民郵電出版社， 2013.

［4］ 劉鴻文. 材料力學I［M］. 第5版. 北京： 高等教育出版社， 2010.

［5］ 屠鳳蓮. 基于ANSYS的支撐架特征值屈曲分析［J］.河北工業大學學報， 2010，39（3）： 6-10.

［6］ 江曉峰. 有限單元法之梁柱單元的屈曲分析精度［J］. 結構工程師， 2010，26（5）： 20-25.

［7］ 余娟. 基于ANSYS的天線桿屈曲分析［J］. 計算機與數字工程， 2013，41（9）： 1523-1528.

Application of Response Surface Methodology in Linear Buckling Analysis of Optimization of Ship Pillar Based on ANSYS

Huang Ji， Lv Hong-guan， Yan Jin， Ye Jian-zhao
（Guangdong Ocean University， Guangdong Zhanjian 524088， China）

With the rapid development of FEM technology and computer software & hardware， the structural optimization theory and algorithms have great progress and development， so more and more engineers pay attention to it. In the paper， using the Static Structural module and Design Exploration module of ANSYS and considering the column stability， the linear buckling analysis of the ship pillar is done. After the first-order linear buckling factor is gained， the structure is optimized. Through the analysis and comparison of the optimizing data， the best structure optimization scheme of pillar structure is gained. It is significant to the real engineering applications.

structural optimization； linear buckling； column stability； ship pillar

U661.43

A

10.14141/j.31-1981.2016.01.007

廣東省青年創新人才類項目（2014KQNCX086）。

黃技（1988—），男，助教，研究方向：船舶結構設計。