遺傳算法在水電站廠內經濟運行中的應用
焦國彬
(湖南澧水流域水利水電開發有限責任公司 湖南常德 415311)
遺傳算法在水電站廠內經濟運行中的應用
焦國彬
(湖南澧水流域水利水電開發有限責任公司 湖南常德 415311)
遺傳算法是一種通過模擬達爾文生物進化論的自然選擇和遺傳機理的計算模型,通過模擬自然進化的過程,能夠得到最優解。本文將對遺傳算法的實現方法進行介紹,然后根據實例詳細探究其在水電廠內經濟運行中的應用。
遺傳算法;水電站廠;經濟運行
1 引言
水電廠經濟運行包括時間最優化以及空間最優化兩點,傳統的動態規劃法搜索速度較慢,實時性較差。而基因遺傳算法不僅搜索速度較快,而且能夠獲得全局最優解,已經被廣泛應用于水電廠經濟運行研究中。
2 遺傳算法的實現
2.1 表示結構和處理約束條件
通過遺傳算法計算出的解有兩種表示方法,分別是二進制向量以及浮點向量。如果使用二進制向量作為一個染色體,將其作為決策變量的真實值,則向量的長度與要求的精度有較大的關聯,如果需要解決的優化問題比較復雜,則二進制向量表示結構難度較大:如果采用浮點向量,每一個浮點向量可以表示為一個染色體,其長度與解向量相同,向量X=(X1,X2…Xn)可以用來表示最優化問題的解,相應的染色體也可以表示為V=(X1,X2…Xn)。
2.2 初始化過程
隨機產生一定數目的初始染色體,并且將其組成一個種群,其中染色體數量可以稱為種群規模。定義整數pop,使其代表染色體的個數,在計算過程中隨機產生pop個初始染色體。具體做法是:先給出可行集中的一個內點,記為V0,定義一個較大的數值M。在Rn中,隨機選擇一個方向d,如果V0+M·d能夠符合不等式約束,則可以將V=V0+M·d作為一個染色體,否則,則置M為0和M之間的一個隨機數,直到V0+M·d可行。由于Vn是內點,因此必然能夠找到滿足不等式約束的可行解。最后重復上述步驟,產生pop個初始染色體V1,V2…Vpop。
2.3 評價函數
對于每個染色體的優劣,可以使用評價函數進行科學合理的評價,具體指的是將染色體對環境的適應度作為遺傳操作的主要依據。
對各個染色體V1,V2…Vpop的目標函數值進行計算,然后根據好壞進行排列,并且定義評價函數:

其中:i=1表示染色體是最為優秀的,而i=pop指的是染色體是最差的。
2.4 選擇過程
染色體的選擇過程指的是從種群中優選出最為優秀的染色體,如果染色體的適應度較高,則其被選中的概率也就越高。通過染色體選擇的過程,可以產生出一個全新的種群。
對于每一個染色體,計算累積概率qi:

從區間(0,qpop)中產生一個隨機數 r,如果 qi-1 2.5 交叉過程 (1)將p4作為交叉概率; (2)從第i=1到pop重復,重復選擇步驟共pop次:從區間[0,1]中產生一個隨機數r,如果r (3)將 V11,V21,V31,…作為上述步驟所選擇出的父代,然后將所有的父代隨機分未(V11,V21),(V31,V41),(V51,V61)…; (4)從區間(0,1)中產生隨機數C,然后根據以下形式交叉操作: 對每個后代進行檢驗,檢查其可行性,如果兩個后代都具有可行性,則可以將其作為父代,反之只能保留其中一個,然后產生新的隨機數C,重復上述步驟,直到獲得兩個具有可行性的后代。 2.6 變異過程 (1)定義變異概率Pm。 (2)由i=1到pop重復以下步驟,共計pop次:從區間(0,1)中隨機選擇 r,如果 r 3.1 基本情況 該水電廠設計引用發電流量為480m3/s,總共裝機3臺,單機2萬kW,單機引用流量156.12m3/s,在水頭為13m時,單機最大出力為1.8萬kW。 3.2 數學模型 機組間負荷優化分配模型的數學表達式為: 式中:N——指的是系統給定水電站的總負荷值; Q——指的是水電站機組引用的總流量; Ni——指的是第i臺機組承擔的負荷,i=1,2,…,n; Qi——指的是第i臺機組引用的流量,i=1,2,…,n。 3.3 計算步驟 (1)選擇決策變量,確定約束條件。 其中:N小=0.5萬kW; N大=1.8萬kW。 (2)建立優化模型。 式中:Q指的是第i臺機水輪機出Ni的出力所需的流量。 (3)確定編碼方法。 決策變量N1、N2用長度為l0位的二進制編碼串來表示。可以將N1、N2的定義域離散化為1023個大小相等的區域。將分別表示N1、N2的兩個二進制編碼形成染色體編碼方法。 (4)確定解碼方法。 在解碼過程中,需要將20位長的二進制編碼串進行切斷,分為兩個10位長的二進制編碼串,并且分別將其轉換為對應的十進制整數代碼,記為y1,y2。將代轉換為變量的解碼公式為: 在此過程中,需要保證N小≤N3=N總-N1-N2≤N大。然后通過Qi(Ni)曲線插值計算得出Qi(i=1,2,3)。如果結果無法滿足約束條件的時候,則可以加入罰函數。罰函數為:(x3-1.8)1.010。 (5)確定個體評價方法。 目標函數總是正數,可以將個體的適應度取為: (6)確定遺傳算法的運行參數。 群體大小:MaxPopsize=500。 終止代數:GENETATION=200。 交叉概率:Pr=0.6,變異概率:Pm=0.001。 3.4 計算成果 將上述步驟進行組合,通過程序計算,可以輸出最優負荷分配Ni=1.8萬kW,N2=1.8萬kW,N3=1.2萬kW和最小流量Q=416m3/s。 交叉概率=0.6,Pm=0.001,POPSIZE=500,Hc=13.0m,計算結果如表 1所示。 通過上述計算得知,隨著Pc、Pm的變化,最優解幾乎保持不變。如果迭代次數沒有達到足夠大,則通過搜索所得到的只是局部最優解,當迭代次數為100次時達到全局最優解416m3/s,當種群規模增加一倍,則出現最優值的概率就會減小一倍,由此可見遺傳算法的尋優與迭代次數和種群規模有很大的關聯。另外,參數對變異概率和交叉概率的靈敏度較低,因此,優化結果幾乎保持不變,具體如表2~5所示。 表1 遺傳算法實現水電站最優機組負荷分配成果表 表2 變異概率對優化結果的影響 表3 迭代次數對優化結果的影響 表4 種群規模對優化結果的影響 表5 變異概率對優化結果的影響 綜上所述,通過使用遺傳算法對水電站的優化運行進行計算,不僅能夠提高水電廠運行經濟效益,而且能夠較好的滿足水電廠經濟運行實時性要求,值得推廣使用。 [1]沈圣,黃煒斌,李基棟,等.巨型水電站廠內經濟運行及效益分析[J].電網技術,2015(09):2478~2482. [2]王利卿,王振飛.水電站經濟運行最小能耗模型研究[J].河南水利與南水北調,2015(16):63~62. [3]黃家輝.水電站優化運行探討[J].電工技術:理論與實踐,2015(09):152. TV737 A 1004-7344(2016)08-0100-02 2016-3-1 焦國彬(1984-),男,助理工程師,本科,主要從事水電站運行等工作。
3 某水電站廠內經濟運行






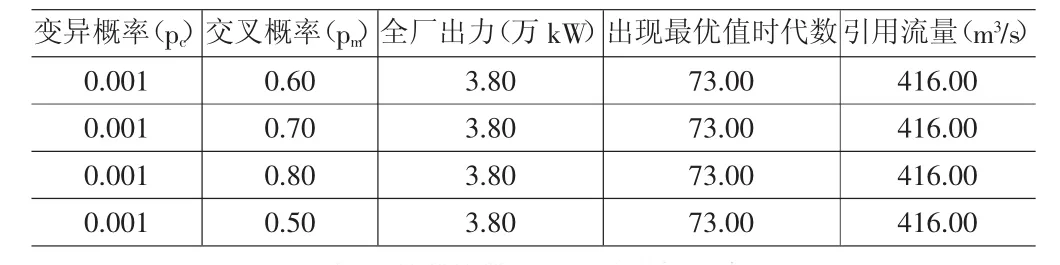
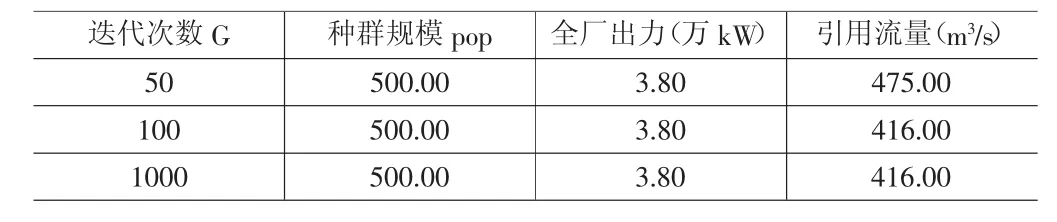


4 結語

