瞬態(tài)統(tǒng)計能量分析法中動態(tài)響應誤差分析
宋海洋,于開平,李向陽,韓敬永
(哈爾濱工業(yè)大學 航天學院,黑龍江 哈爾濱 150001)
瞬態(tài)統(tǒng)計能量分析法中動態(tài)響應誤差分析
宋海洋,于開平,李向陽,韓敬永
(哈爾濱工業(yè)大學 航天學院,黑龍江 哈爾濱 150001)
統(tǒng)計能量分析方法能夠有效預示艦船和車輛等結(jié)構的高頻振動及噪聲。本文通過建立兩子結(jié)構耦合模型,利用差分法研究了瞬態(tài)統(tǒng)計能量分析中參數(shù)誤差對子結(jié)構響應能量的影響,同時給出了參數(shù)誤差與所導致能量誤差的關系函數(shù)。結(jié)果表明:對于外載荷直接激勵的子結(jié)構,內(nèi)損耗因子和耦合損耗因子的誤差都會導致被預示總能量的減小。對于外載荷間接激勵的子結(jié)構,內(nèi)損耗因子的誤差會導致峰值能量的減小,而耦合損耗因子的誤差會導致峰值能量的增加。本文內(nèi)容對改進動力學系統(tǒng)數(shù)值模型以及提高結(jié)構振動和噪聲預示精度有一定的幫助。
瞬態(tài)統(tǒng)計能量分析;參數(shù)誤差;能量誤差
0 引 言
解決復雜結(jié)構振動和噪聲問題的方法包括有限元法、邊界元法、模態(tài)分析法、波動分析法、阻抗導納功率流法、結(jié)構聲強法和統(tǒng)計能量分析法,其中統(tǒng)計能量分析法是目前公認的解決復雜結(jié)構高頻振動問題最有效的方法。經(jīng)過幾十年的研究和探索,統(tǒng)計能量分析方法不但在理論上有了創(chuàng)新和突破,而且已經(jīng)成功地應用到了船舶[1-3]和車輛[4]等領域來解決復雜結(jié)構的振動和噪聲問題。
采用瞬態(tài)統(tǒng)計能量分析法進行動力學系統(tǒng)環(huán)境預示需要確定結(jié)構 2 個基本參數(shù):內(nèi)損耗因子和耦合損耗因子。這 2 個參數(shù)的準確估算對結(jié)構響應的預示和數(shù)值仿真結(jié)果的精度有重要的影響。其中內(nèi)損耗因子是衡量系統(tǒng)阻尼特性、決定振動能量耗散的重要參數(shù)。耦合損耗因子是統(tǒng)計能量分析中表征耦合系統(tǒng)間能量交換的重要參數(shù)。目前除了一些簡單結(jié)構的內(nèi)損耗因子和耦合損耗因子可以從理論上推得,比較復雜的結(jié)構的內(nèi)損耗因子和耦合損耗因子只能通過實驗測量來得到[5-8]。然而內(nèi)損耗因子和耦合損耗因子在很多情況下是 10–2~10–4數(shù)量級的小數(shù),在實際工作中要對這些小數(shù)進行運算和測量很困難,故這些參數(shù)的測量結(jié)果經(jīng)常存在不同程度的誤差。
本文基于 2 個耦合子結(jié)構所組成的系統(tǒng),分析了瞬態(tài)統(tǒng)計能量分析法中參數(shù)誤差對子結(jié)構能量的影響,給出了參數(shù)誤差與所導致能量誤差的關系函數(shù),對改進動力學系統(tǒng)數(shù)值模型及提高數(shù)值模擬的精度有很大的幫助。
1 瞬態(tài)統(tǒng)計能量分析中參數(shù)誤差對子結(jié)構能量影響
1.1 內(nèi)損耗因子誤差對子結(jié)構能量的影響
兩子結(jié)構耦合的統(tǒng)計能量分析模型如圖 1 所示,瞬間能量平衡方程可寫為:

其中:Ei(t)(i=1,2) 是帶寬 Δω 內(nèi)隨時間變化的總能量,代表總能量對時間的一階導數(shù),ηi(i=1,2) 是子結(jié)構 i 的內(nèi)損耗因子,代表子結(jié)構 i 與子結(jié)構 j 間的耦合損耗因子,ω 為分析帶寬Δω 的中心頻率。現(xiàn)給子結(jié)構 1 施加一個短時的脈沖激勵力,那么子結(jié)構 1 的初始能量為而子結(jié)構 2 的初始能量為 0 且輸入功率 P1=P2=0。
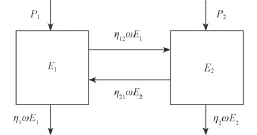
圖 1 兩子結(jié)構的統(tǒng)計能量分析模型Fig. 1 SEA model for two coupled subsystems

采用拉普拉斯變換方法可得兩子結(jié)構隨時間變化的能量表達式為:

其中:


① 當兩子結(jié)構滿足時,將式(5)整理后得:
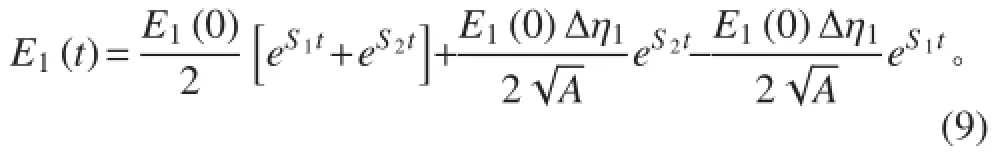

將式(10)代入式(6)中可得子結(jié)構 2 的峰值能量為

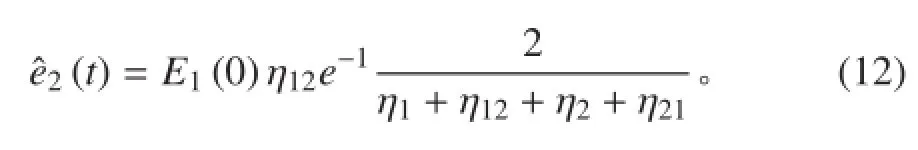
那么子結(jié)構 2 峰值能量的相對誤差為
1.2 耦合損耗因子誤差對子結(jié)構能量的影響
其中:


② 通過計算可得到子結(jié)構 2 的峰值能量為

得子結(jié)構 2 的峰值能量為

子結(jié)構 2 峰值能量的相對誤差為

2 計算實例
如圖 2 所示,系統(tǒng)由兩塊相互垂直并鉚接的鋼板組成,并且兩塊鋼板的其他邊界條件是自由的。鋼板的密度為 7 800 kg/m3。板 1 的長度為 0.42 m,寬度為0.36 m,厚度為 0.01 m。板 2 的長度為 0.42 m,寬度為0.36 m,厚度為 0.004 5 m。以上2塊鋼板的內(nèi)損耗因子和耦合損耗因子已經(jīng)在文獻[9]中由實驗測量得到,表 1展示了兩板在中心頻率 f=2 000 Hz 時測量的內(nèi)損耗因子和耦合損耗因子。

圖 2 兩板耦合系統(tǒng)Fig. 2 Two-plate coupling structural system

表 1 兩板在中心頻率 f = 2 000 Hz 時內(nèi)損耗因子和耦合損耗因子測量值Tab. 1 Measured values of damping loss factors and coupling loss factors at f = 2 000 Hz
現(xiàn)對板 1 施加一個短時的脈沖激勵,使板 1 具有初始能量 E1(0)=1 kJ,通過式(13)和式(21)可以得到板 2 的峰值能量相對誤差和板 1 參數(shù)相對誤差的關系曲線,如圖 3 和圖 4 所示。

圖 3 板 2 的峰值能量相對誤差與板 1 內(nèi)損耗因子相對誤差關系Fig. 3 The relation between peak energy error of plate 2 and damping loss factor error of plate 1

圖 4 板 2 的峰值能量相對誤差與板 1 耦合損耗因子相對誤差關系Fig. 4 The relation between peak energy error of plate 2 and coupling loss factor error of plate 1
圖 3 表明增大板 1 的內(nèi)損耗因子,將引起板 2 峰值能量的降低,因為增加的阻尼過多消耗了板 1 的能量,導致傳遞到板 2 的能量減少。圖 4 表明增加板 1對板 2 的耦合損耗因子,實際增大了板 1 對板 2 能量的傳遞,導致板 2 峰值能量的增加。因此精確確定內(nèi)損耗因子和耦合損耗因子盡量減少測量誤差對瞬態(tài)統(tǒng)計能量分析中結(jié)構能量的預示精度有較大的影響。
3 結(jié) 語
本文從兩耦合子結(jié)構所組成系統(tǒng)的能量平衡方程入手,借助拉普拉斯變換研究了瞬態(tài)統(tǒng)計能量分析法中參數(shù)誤差對子結(jié)構總能量的影響,同時給出了參數(shù)誤差與所導致能量誤差的關系函數(shù)。對于外載荷直接激勵的子結(jié)構,內(nèi)損耗因子和耦合損耗因子的誤差都會導致總能量的減小。對于外載荷間接激勵的子結(jié)構,內(nèi)損耗因子的誤差會導致峰值能量的減小,而耦合損耗因子的誤差會導致峰值能量的增加。不同于穩(wěn)態(tài)統(tǒng)計能量分析理論,在瞬態(tài)統(tǒng)計能量分析中,求解 3 個及以上子結(jié)構組成的系統(tǒng)的精確能量解是很復雜的,后續(xù)需要更多數(shù)學方法的發(fā)展和引進,本文內(nèi)容對于 2 個以上的子結(jié)構組成的復雜系統(tǒng)將有一定參考意義。
[1]HYNNá P, KLINGE P, VUOKSINEN J. Prediction of structureborne sound transmission in large welded ship structures using statistical energy analysis[J]. Journal of Sound and Vibration,1995, 180(4): 583–607.
[2]邵亮. 統(tǒng)計能量法在船舶艙室噪聲預報中的應用[J]. 艦船科學技術, 2012, 34(5): 98–100, 107. SHAO Liang. Prediction and research of ship cabin noise with statistical energy analysis[J]. Ship Science and Technology,2012, 34(5): 98–100, 107.
[3]YAYLADERE B C, ?ALI?KAN M. Prediction of noise levels within a submerged vessel by statistical energy analysis[C]//Proceedings of the 20th International Congress on Sound & Vibration. Bangkok, Thailand: ICSV, 2013: 66–71.
[4]CHEN S M, WANG D F, LEI Y F. Automotive interior noise prediction based on single sound cavity using statistical energy analysis method[J]. Noise & Vibration Worldwide, 2011,42(11): 36–43.
[5]程廣利, 朱石堅, 伍先俊. 統(tǒng)計能量分析法及其損耗因子確定方法綜述[J]. 船舶工程, 2004, 26(4): 10–15. CHENG Guang-li, ZHU Shi-jian, WU Xian-jun. A summary of statistical energy analysis method and its loss factor’s determination[J]. Ship Engineering, 2004, 26(4): 10–15.
[6]葉敏, 郎作貴, 郝志勇. 復雜系統(tǒng)振動能量平衡方程中SEA參數(shù)的測定[J]. 內(nèi)燃機學報, 1998, 16(4): 469–474. YE Min, LANG Zuo-gui, HAO Zhi-yong. The determination of vibration energy balance sea system parameters in a complex structure[J]. Transactions of CSICE, 1998, 16(4): 469–474.
[7]盛美萍, 王敏慶, 孫進才, 等. 非保守耦合系統(tǒng)的等效內(nèi)損耗因子[J]. 聲學學報, 1997, 22(6): 555–561. SHENG Mei-ping, WANG Min-qing, SUN Jin-cai, et al. Equivalent internal loss factors for non-conservatively coupled systems[J]. Acta Acustica, 1997, 22(6): 555–561.
[8]盛美萍, 王敏慶, 孫進才. 非保守耦合系統(tǒng)的耦合損耗因子[J].聲學學報, 1999, 24(5): 550–556. SHENG Mei-ping, WANG Min-qing, SUN Jin-cai. The coupling loss factors of non-conservatively coupled systems[J]. Acta Acustica, 1999, 24(5): 550–556.
[9]MAO B Y, XIE S L, XU M L, et al. Simulated and experimental studies on identification of impact load with the transient statistical energy analysis method[J]. Mechanical Systems and Signal Processing, 2014, 46(2): 307–324.
Analysis on dynamic response error in transient
SONG Hai-yang, YU Kai-ping, LI Xiang-yang, HAN Jing-yong
(Department of Astronautical Science and Mechanics, Harbin Institute of Technology, Harbin 150001, China)
Statistical energy analysis (SEA) method has been recognized as a powerful tool in predicting the highfrequency sound and vibration of ship structures and vehicles. In the transient statistical energy analysis framework, this paper applies the difference method to investigate the effect of parameters error on structural total energy. Meanwhile, the function relation of parameters error and caused energy error is also provided. The following results can finally be shown. For the subsystem that is directly excited by an external load, the error of the damping loss factors and coupling loss factors will result in the decrease of structural total energy. For the subsystem that is indirectly excited, the error of damping loss factors can lead to the decreasing of structural peak energy, while the error of coupling loss factors will result in the increase of structural peak energy. The content of this paper can provide some help for improving the dynamics model and predicted accuracy of sound and vibration.
transient statistical energy analysis;parameter error;energy error
V415.4
A
1672 – 7619(2016)04 – 0038 – 04
10.3404/j.issn.1672 – 7619.2016.04.008
2015 – 07 – 02;
2015 – 09 – 20
國家自然科學基金 資助項目(11372084)
宋海洋(1986 – ),男,博士,研究方向為高頻振動和噪聲環(huán)境的預示。

