緊扣概念 把握實質
王亞
?
緊扣概念 把握實質
王亞
蘇科版《數學》九年級下冊沒有給出“坡角”和“坡度”的具體概念,僅僅是在第113頁問題1中給出了斜坡的坡角和坡度i的意義.
如圖1所示,斜坡AB的坡角就是其與水平線的夾角∠A,斜坡AB的坡度i= tanA.
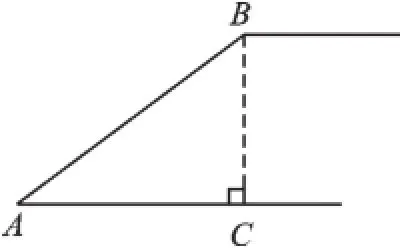
圖1
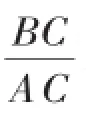
1.斜坡AB的坡度i越大,斜坡的坡角A就越大,其坡面AB就越陡;斜坡AB的坡度i越小,斜坡的坡角A就越小,其坡面AB就越平緩.
2.斜坡的水平寬度一定時,鉛直高度越高,則斜坡的坡角A就越大,斜坡AB的坡度i越大,其坡面AB就越陡;斜坡的水平寬度一定時,鉛直高度越低,則斜坡的坡角A就越小,斜坡AB的坡度i越小,其坡面AB就越平緩.
解決這類問題的關鍵是將實際問題抽象為數學問題,把握其隱含的本質特征,建立直角三角形的數學模型,并應用三角函數加以解答.現舉例加以說明,以期幫助同學們在遇到此類問題時掃除障礙.
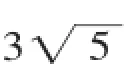
A.5米B.6米
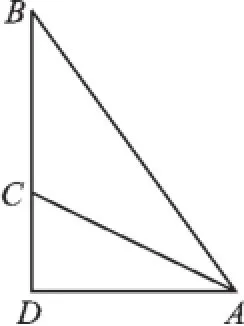
圖2
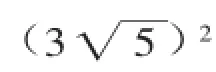
【點評】本題考查了應用解直角三角形的知識解決與坡度、坡角相關的實際問題,解題的關鍵是理解坡度的概念,把握其實質建立直角三角形并利用勾股定理建立方程求得結果.
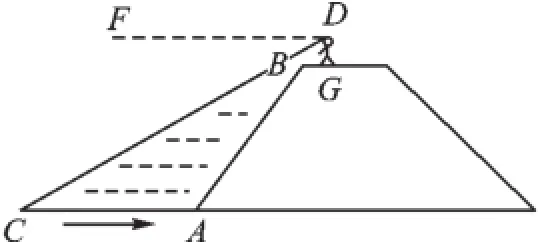
圖3
例2(2015·十堰)如圖3,小華站在河岸上的G點,看見河里有一小船沿垂直于岸邊的方向劃過來.此時,測得小船C的俯角是∠FDC=30°,若小華的眼睛與地面的距離是1.6米,BG=0.7米,BG平行于AC所在的直線,迎水坡的坡度i=4∶3,坡長AB=8米,點A,B,C,D,F,G在同一個平面上,則此時小船C到岸邊的距離CA的長為_______米.(結果保留根號)
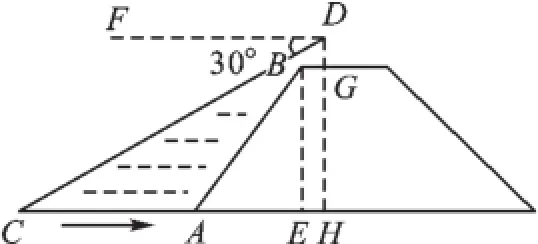
圖3
【分析】由條件,我們可以先構造Rt△ABE 和Rt△CDH,然后根據坡度分別計算出AE 和BE的長,從而求出AH和DH的長.最后在Rt△CDH中,利用tan30°的三角函數求出CH的長,再減去AH的長即可求出小船C到岸邊的距離CA的長.
解:延長DG,交CA延長線于點H,過點B作BE⊥AH,垂足為點E,則DH⊥CH,垂足為H.
設BE=4x,AE=3x,則AB=5x,
∵∠FDC=30°,∴∠C=30°,
【點評】本題以河岸迎水坡的坡度為問題背景,考查了同學們對坡度概念的理解,解答本題的關鍵在于構建直角三角形,應用圖形中隱含的線段之間的比值、三角函數和勾股定理,建立方程解決問題.
例3如圖4,某市防洪指揮部發現江邊一處長400米,高8米,背水坡的坡角為45°的防洪大堤(橫截面為梯形ABCD)急需加固.經調查論證,防洪指揮部專家組制定的加固方案是:背水坡面用土石進行加固,并使上底加寬2米,加固后,背水坡EF的坡度i= 1∶2.
(1)求加固后壩底增加的寬度AF的長;
(2)求完成這項工程需要土石多少立方米?
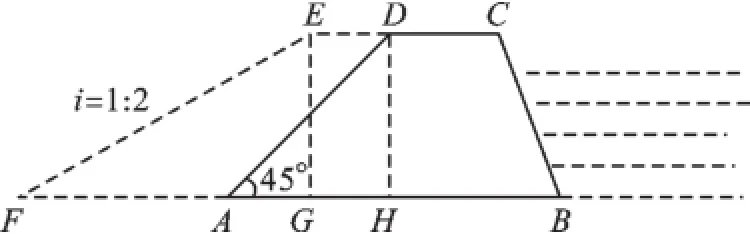
圖4
【分析】(1)由于梯形ABCD的兩底是平行的,則點D、E到底邊AB的距離是相等的,不妨分別過點E、點D作AB的垂線,設垂足為G、H.因而,在Rt△EFG中,可以根據坡面的鉛直高度(即壩高)及坡比,求出FG的長,同理可在Rt△ADH中求出AH的長,再由AF=FG+GH-AH求出AF的長.
(2)梯形AFED的面積乘以壩長即為所需的土石的體積.根據(1)中求得的線段長度,可以先求得梯形AFED的面積,再求得這項工程需要土石的立方米數.
解:(1)分別過點E、D作EG⊥AB、DH⊥AB交AB于G、H,
∵四邊形ABCD是梯形,且AB∥CD,
∴DH平行且等于EG,
∴四邊形EGHD是矩形,∴ED=GH.
在Rt△ADH中,∠AHD=90°,∠DAH=45°,
∴AH=DH=8(米),
∴FG=2EG=16(米),
∴AF=FG+GH-AH=16+2-8=10(米).
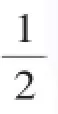
答:(1)加固后壩底增加的寬度AF為10米;(2)完成這項工程需要土石19 200立方米.
【點評】本題以某市防洪指揮部專家組制定的加固方案所需土石的立方數為問題背景,考查同學們能否靈活應用坡度的概念,把握問題的實際本質,構建直角三角形,應用三角函數化歸數學問題,使得問題迎刃而解.
(作者單位:江蘇省建湖縣匯文實驗初中教育集團匯文校區)

