“銳角三角函數”數學思想面面觀
陸中明
?
思維訓練營/思想方法
CHU ZHONG SHENG SHI JIE
“銳角三角函數”數學思想面面觀
陸中明

數學思想是數學的靈魂、精髓.學習數學不僅僅要掌握數學知識,同時還要掌握數學知識中所隱含的思想方法.本文將對“銳角三角函數”中蘊含的數學思想加以分析,以期對提高同學們數學素養有所幫助.
一、一一對應思想
由相似的直角三角形可以知道,它們的邊與邊的比值隨銳角大小的變化而變化,隨著銳角大小的確定而惟一確定.同樣,借助計算器根據銳角大小可以求得其三角函數值,反過來,借助計算器根據三角函數值可以求得對應的銳角大小.
例1(2015·陜西)如圖1,有一滑梯AB,其水平寬度AC為5.3米,鉛直高度BC為2.8米,則∠A的度數約為_______.(用科學計算器計算,結果精確到0.1°)
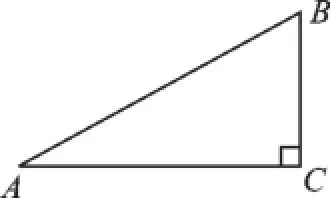
圖1
【點評】本題考查了用計算器由三角函數值求銳角的度數,解題的關鍵是掌握由三角函數值求銳角度數的方法.
二、轉化思想
轉化思想是初中數學中常用的數學思想,通過轉化,可以把未知的關系轉化為已知的條件,把陌生的問題轉化為熟悉的問題,把復雜的問題轉化為相對容易的問題.
例2(2015·桂林)如圖2,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足為D,則tan∠BCD的值是_______.
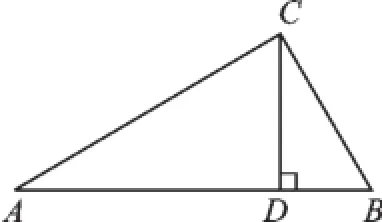
圖2
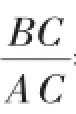
【點評】本題既考查了對正切概念的掌握,也考查了靈活應用轉化思想將問題中不常見的角轉化為熟悉的直角三角形的銳角進行求解.
三、方程思想
方程思想是一種重要的數學思想,所謂方程思想是指從問題的數量關系入手,將問題中的已知量和未知量之間的數量關系通過適當設元建立方程(組),然后通過解方程(組)使問題得到解決的思想方式.
例3(2015·云南)為解決江北學校學生上學過河難的問題,鄉政府決定修建一座橋.建橋過程中需測量河的寬度(即兩平行河岸AB與MN之間的距離).在測量時,選定河對岸MN上的點C處為橋的一端,在河岸點A處,測得∠CAB=30°,沿河岸AB前行30米后到達B處,在B處測得∠CBA=60°.請你根據以上測量數據求出河的寬度.(參考數據:≈1.41,≈1.73;結果保留整數)
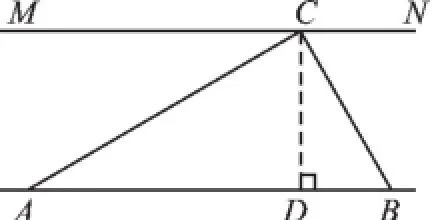
圖3
【解析】過點C作CD⊥AB,垂足為D,構造Rt△ACD和Rt△BCD這兩個直角三角形. 設CD=x,分別在這兩個三角形內,利用已知角的正切,用x表示出AD、BD的值,然后根據AB=AD+BD,列方程即可求解.
【解答】過點C作CD⊥AB,垂足為D,
∵AB=AD+DB=30,
答:河的寬度為13米.
【點評】本題考查了解直角三角形的實際應用、方程思想,解題的關鍵是構造直角三角形,根據已知條件列方程.
四、數形結合思想
數形結合就是根據數學問題的題設和結論之間的內在聯系,既分析其數量關系,又揭示其幾何意義,使數量關系和幾何圖形巧妙地結合起來,并充分地利用這種結合,探求解決問題的思路,使問題得以解決的數學思想方法.
例4(2015·綿陽)如圖4,要在寬為22米的九洲大道AB兩邊安裝路燈,路燈的燈臂CD長為2米,且與燈柱BC成120°角,路燈采用圓錐形燈罩,燈罩的中軸線DO與燈臂CD垂直,當燈罩的軸線DO通過公路路面的中心線時照明效果最佳.此時,路燈的燈柱BC高度應該設計為().
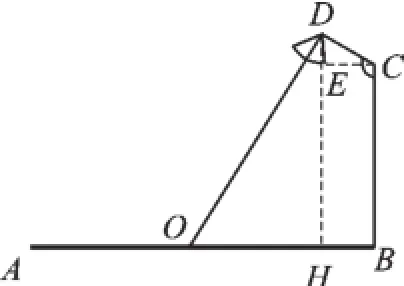
圖4
【解析】設燈柱BC的長為h米,過點D作DH⊥AB于點H,過點C作CE⊥DH于點E.
∴四邊形BCEH為矩形.
∵∠DCB=120°,∴∠DCE=30°.
又∵∠CDO=∠CBO=90°,
∴∠DOB=60°.
∵在Rt△DCE中,
∴DE=CD·sin30°=1,CE=CD·cos30°=
在Rt△DOH中,
因此,本題應該選D.
【點評】解答這類問題的關鍵是通過作垂線構造直角三角形,這是添加輔助線的常見方式,將非直角三角形問題轉化為直角三角形問題,便于運用三角函數關系和勾股定理來解題.
五、模型思想
從現實生活或具體情境中抽象出數學問題,用數學符號建立銳角三角函數表示實際問題中的數量關系和變化規律,求出結果并討論結果的意義.
例5(2015·鹽城)如圖5所示,一幢樓房AB背后有一臺階CD,臺階每層高0.2米,且AC=17.2米.設太陽光線與水平地面的夾角為α,當α=60°時,測得樓房在地面上的影長AE=10米.現有一只小貓睡在臺階的MN這層上曬太陽.
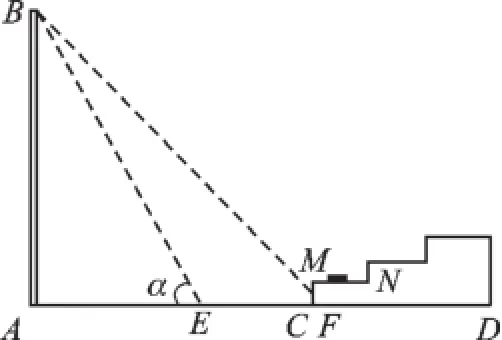
圖5
(2)過了一會兒,當α=45°時,問小貓能否還曬到太陽?請說明理由.
解:(1)當α=60°時,在Rt△ABE中,
答:樓房的高度約為17.3米.
(2)小貓仍可以曬到太陽.
理由如下:
假設沒有臺階,當α=45°時,從點B射下的光線與地面AD的交點為點F,與MC的交點為點H.
∵∠BFA=45°,
∴AF=BA=17.3,即此時的影長為17.3米,
∴CF=AF-AC=17.3-17.2=0.1,
∴CH=CF=0.1(米),
∴大樓的影子才到臺階MC這個側面上,
∴小貓仍曬到太陽.
【點評】本題考查了有關銳角三角函數的應用問題,解題的關鍵是構造直角三角形模型,尋找直角三角形中合適的邊角關系解決問題.
(作者單位:江蘇省建湖縣匯文實驗初中教育集團匯文校區)

