無(wú)人機(jī)自主著陸縱向控制律設(shè)計(jì)

高九州，賈宏光

(1.中國(guó)科學(xué)院 長(zhǎng)春光學(xué)精密機(jī)械與物理研究所， 吉林 長(zhǎng)春 130033；2.中國(guó)科學(xué)院大學(xué)，北京 100039)

?

無(wú)人機(jī)自主著陸縱向控制律設(shè)計(jì)

高九州1，2*，賈宏光1

(1.中國(guó)科學(xué)院 長(zhǎng)春光學(xué)精密機(jī)械與物理研究所， 吉林 長(zhǎng)春 130033；2.中國(guó)科學(xué)院大學(xué)，北京 100039)

針對(duì)無(wú)人機(jī)的自主高精度定點(diǎn)著陸，應(yīng)用自適應(yīng)內(nèi)模控制(AIMC)原理設(shè)計(jì)了自主著陸縱向飛行控制律。以輪式無(wú)人機(jī)為平臺(tái)，將縱向非線性模型解耦并線性化。然后，以地速和下沉率為控制目標(biāo)，應(yīng)用AIMC理論設(shè)計(jì)了縱向飛行控制律。通過(guò)對(duì)AIMC濾波參數(shù)進(jìn)行自調(diào)整改善了系統(tǒng)的動(dòng)態(tài)特性，基于對(duì)模型的辨識(shí)增強(qiáng)了系統(tǒng)的魯棒性。在順逆風(fēng)6 m/s的條件下對(duì)AIMC系統(tǒng)進(jìn)行了數(shù)字仿真， 結(jié)果顯示其落點(diǎn)精度達(dá)到前后向30 m范圍內(nèi)。與傳統(tǒng)內(nèi)模控制(IMC)系統(tǒng)相比，提出的自適應(yīng)內(nèi)模控制(AIMC)系統(tǒng)在動(dòng)態(tài)性能和落點(diǎn)精度等方面均有明顯提高。最后，搭建了半物理測(cè)試平臺(tái)，通過(guò)半物理仿真測(cè)試復(fù)現(xiàn)了系統(tǒng)數(shù)字仿真結(jié)果，驗(yàn)證了系統(tǒng)功能的完整性和協(xié)調(diào)性。

無(wú)人機(jī)；自主著陸；自適應(yīng)內(nèi)模控制；縱向飛行控制律；數(shù)字仿真；半物理測(cè)試

1　引　言

自主著陸是輪式無(wú)人機(jī)回收的重要方式之一，其著陸點(diǎn)的特性指標(biāo)較高，對(duì)導(dǎo)航系統(tǒng)和飛行控制系統(tǒng)均提出了嚴(yán)格要求。文獻(xiàn)[1]指出在著陸過(guò)程中，氣動(dòng)參數(shù)會(huì)因地面效應(yīng)發(fā)生明顯變化，同時(shí)風(fēng)場(chǎng)的存在更會(huì)影響定點(diǎn)著陸的精度。文獻(xiàn)[2]采用穩(wěn)態(tài)逆結(jié)合反饋控制器設(shè)計(jì)了自主著陸控制律，文獻(xiàn)[3]在構(gòu)造非線性干擾觀測(cè)器的基礎(chǔ)上設(shè)計(jì)了滑模控制器，在沒(méi)有考慮風(fēng)場(chǎng)的影響下文獻(xiàn)[2-3]的方法均達(dá)到了精確跟蹤著陸航跡的要求。文獻(xiàn)[4-7]分別應(yīng)用神經(jīng)網(wǎng)絡(luò)和魯棒H∞控制算法對(duì)著陸飛控系統(tǒng)進(jìn)行設(shè)計(jì)，并在仿真中加入風(fēng)場(chǎng)，得到了較好的控制效果，但其算法復(fù)雜，工程實(shí)現(xiàn)難度較大。文獻(xiàn)[8]采用LQG/LTR(Linear Quadratic Gaussian/Loop Transfer Recovery)方法設(shè)計(jì)控制律，在風(fēng)場(chǎng)中具有一定的魯棒性。本文針對(duì)自主著陸中高精度著陸點(diǎn)的指標(biāo)要求，提出一種基于自適應(yīng)內(nèi)模原理的控制律設(shè)計(jì)方法[9-14]，對(duì)自主著陸過(guò)程中縱向運(yùn)動(dòng)進(jìn)行控制律設(shè)計(jì)，加入風(fēng)場(chǎng)效應(yīng)，并通過(guò)系統(tǒng)數(shù)字仿真跟蹤著陸預(yù)設(shè)航跡，在線調(diào)整控制參數(shù)，優(yōu)化控制效果。最后進(jìn)行半物理測(cè)試，驗(yàn)證系統(tǒng)軟硬件工作的完整性和協(xié)調(diào)性[15]。

2　控制系統(tǒng)設(shè)計(jì)

本文以某固定翼無(wú)人機(jī)為平臺(tái)，其為V型尾翼布局，采用活塞螺旋槳發(fā)動(dòng)機(jī)，其主要結(jié)構(gòu)及性能參數(shù)如表1所示。

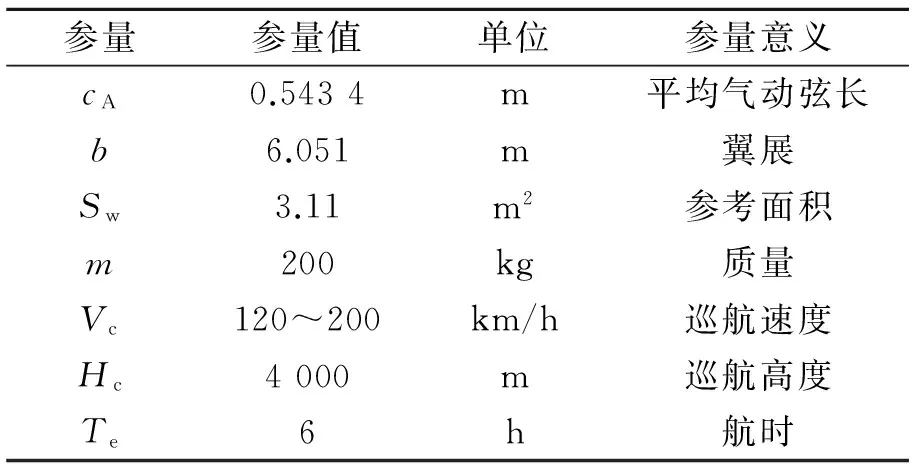
表1　樣例無(wú)人機(jī)結(jié)構(gòu)及性能參數(shù)

2.1自適應(yīng)內(nèi)模控制

內(nèi)模控制是一種基于模型的控制器設(shè)計(jì)方法，通常由被控過(guò)程、過(guò)程模型和含濾波器的內(nèi)模控制器組成，常規(guī)內(nèi)模控制結(jié)構(gòu)如圖1所示。

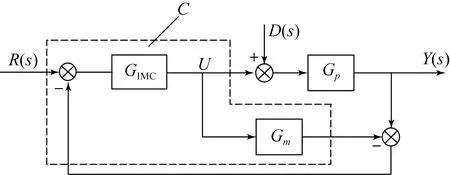
圖1　常規(guī)內(nèi)模控制結(jié)構(gòu)

常規(guī)內(nèi)模控制器的設(shè)計(jì)過(guò)程如式(1)～(3)：

Gm(s)=Gm+(s)·Gm-(s)，

(1)

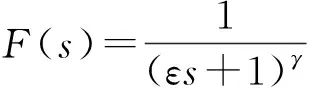
(2)

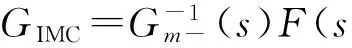
(3)

式中：Gm+(s)和Gm-(s)分別表示過(guò)程模型的不可逆和可逆部分。Gm+(s)通常包括被控對(duì)象Gp(s)的時(shí)滯和右半平面零點(diǎn)環(huán)節(jié)，而Gm-(s) 代表被控對(duì)象Gp(s)具有最小相位特征的部分。ε為濾波器的時(shí)間常數(shù)，γ為濾波器的階數(shù)。

常規(guī)內(nèi)模控制器對(duì)模型的依賴程度較大，且只有一個(gè)可調(diào)的控制參數(shù)，無(wú)法同時(shí)兼顧系統(tǒng)的響應(yīng)特性和魯棒性能。本文在常規(guī)內(nèi)模控制器的基礎(chǔ)上進(jìn)行了改進(jìn)，加入內(nèi)模濾波參數(shù)的自調(diào)整和被控過(guò)程模型估計(jì)環(huán)節(jié)，構(gòu)成自適應(yīng)內(nèi)模控制器。其結(jié)構(gòu)如圖2所示。

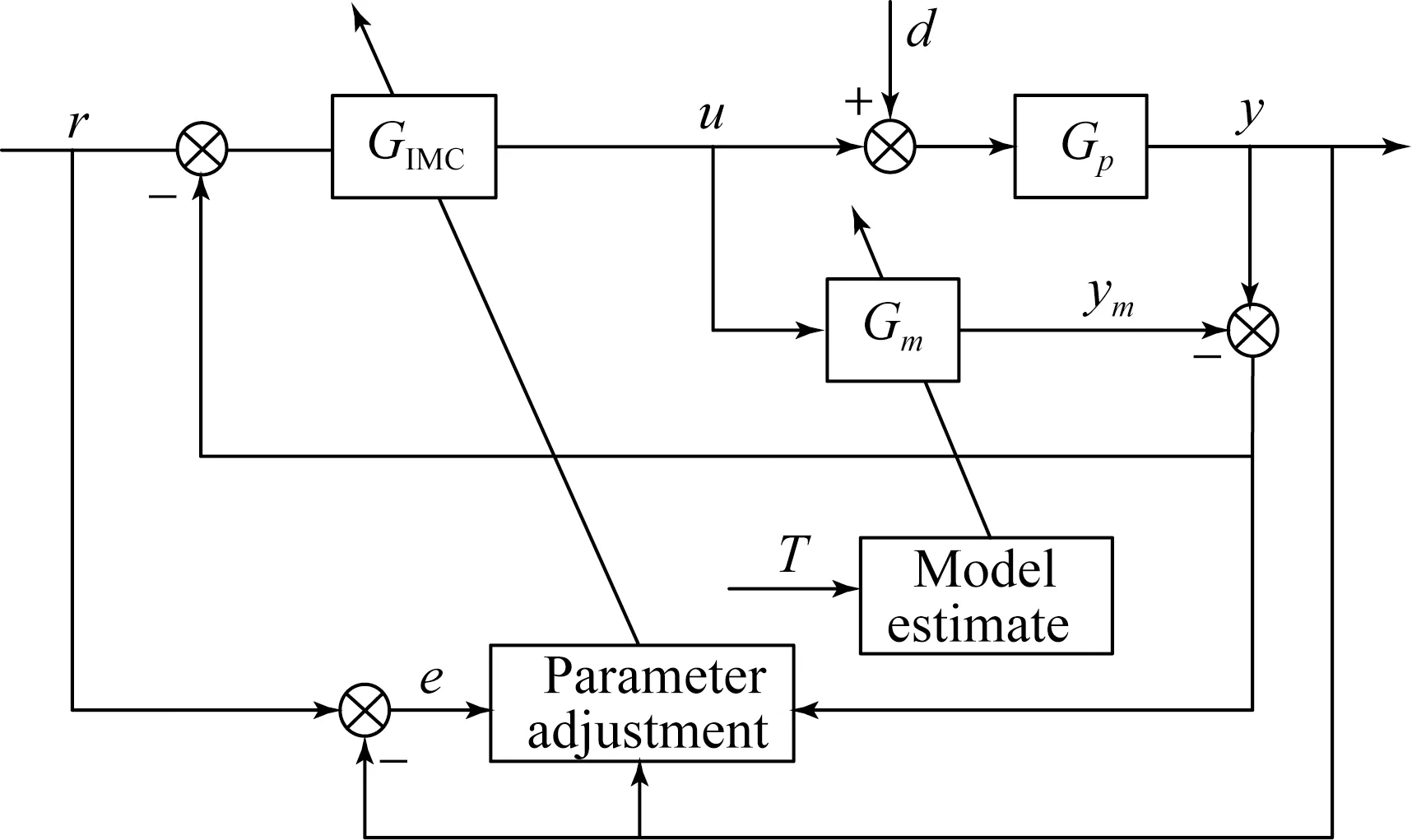
圖2　自適應(yīng)內(nèi)模控制結(jié)構(gòu)

初始設(shè)計(jì)內(nèi)模控制器的濾波參數(shù)ε時(shí)，可取較小值，使系統(tǒng)得到較好的動(dòng)態(tài)特性，當(dāng)模型誤差較大而危及系統(tǒng)穩(wěn)定性時(shí)，自適應(yīng)放大濾波參數(shù)ε，從而保證系統(tǒng)穩(wěn)定。濾波參數(shù)自適應(yīng)律設(shè)計(jì)為：

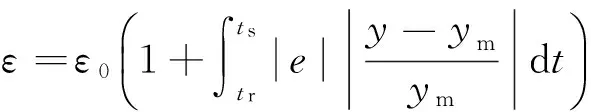
(4)

其中：ε0為初始濾波參數(shù)，e為系統(tǒng)誤差，y為系統(tǒng)輸出，ym為過(guò)程模型輸出，tr為系統(tǒng)輸出首次到達(dá)設(shè)定值的時(shí)間，ts為系統(tǒng)設(shè)定的調(diào)節(jié)時(shí)間。

過(guò)程模型內(nèi)部參數(shù)T的變化將導(dǎo)致過(guò)程模型改變，過(guò)程模型參數(shù)的估計(jì)采用最小二乘法，考慮系統(tǒng)的輸入輸出模型為：

y(n)=-a1y(n-1)-a2y(n-2)-…+

b0u(n-k)+b1u(n-k-1)+…+ω(n)=

φTθ+ω(n).

(5)

其中：φ為輸入輸出觀測(cè)向量，θ為未知參數(shù)向量，ω為噪聲。

φT=[-y(n-1)，y(n-2)，…，y(n-k)，

u(n-m)，u(n-m-1)，…，u(n-m-k)]，

θ=[a1，a2，…，ak，b0，b1，…，bk]，

(6)

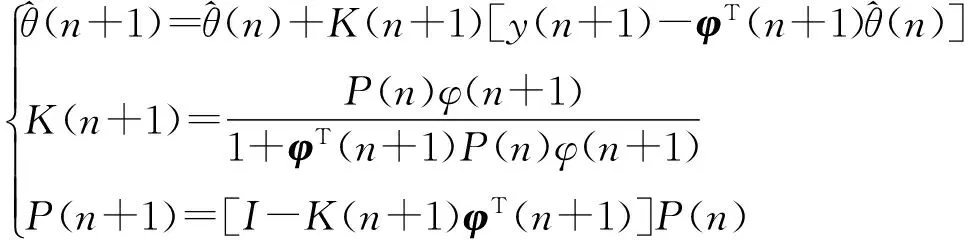
(7)

2.2系統(tǒng)動(dòng)力學(xué)模型

本文在穩(wěn)態(tài)飛行的前提下將飛行運(yùn)動(dòng)進(jìn)行解耦，并利用系數(shù)凍結(jié)法和小擾動(dòng)線性化原理將解耦的非線性縱向運(yùn)動(dòng)進(jìn)行線性化。

縱向狀態(tài)空間表達(dá)式為：

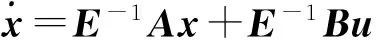
(8)

其中c7為系統(tǒng)結(jié)構(gòu)參數(shù)，其余氣動(dòng)參數(shù)可通過(guò)式(5)～(7)進(jìn)行離線辨識(shí)得到，辨識(shí)數(shù)據(jù)來(lái)源于風(fēng)洞試驗(yàn)，最終得到不同速度和不同高度條件下的過(guò)程模型。風(fēng)動(dòng)測(cè)量數(shù)據(jù)表明，在高度小于30 m時(shí)，由于地面效應(yīng)的影響，氣動(dòng)參數(shù)變化明顯，辨識(shí)得到的過(guò)程模型變化較大。

2.3地速控制

根據(jù)自適應(yīng)內(nèi)模控制原理，利用油門作為控制輸入對(duì)地速進(jìn)行控制，控制結(jié)構(gòu)如圖3所示。

為保證自主著陸的高精度特性，本文采用地速進(jìn)行控制，地速由測(cè)量數(shù)據(jù)北、東、地三者速度經(jīng)濾波和融合處理得到。同時(shí)為保證飛行不失速，對(duì)空速進(jìn)行測(cè)量，當(dāng)空速有失速趨勢(shì)時(shí)，將地速控制切換為空速控制，以進(jìn)行定高盤旋飛行。根據(jù)空速和高度的不同在模型估計(jì)器中調(diào)用相應(yīng)的氣動(dòng)參數(shù)形成地速與油門關(guān)系的過(guò)程模型。

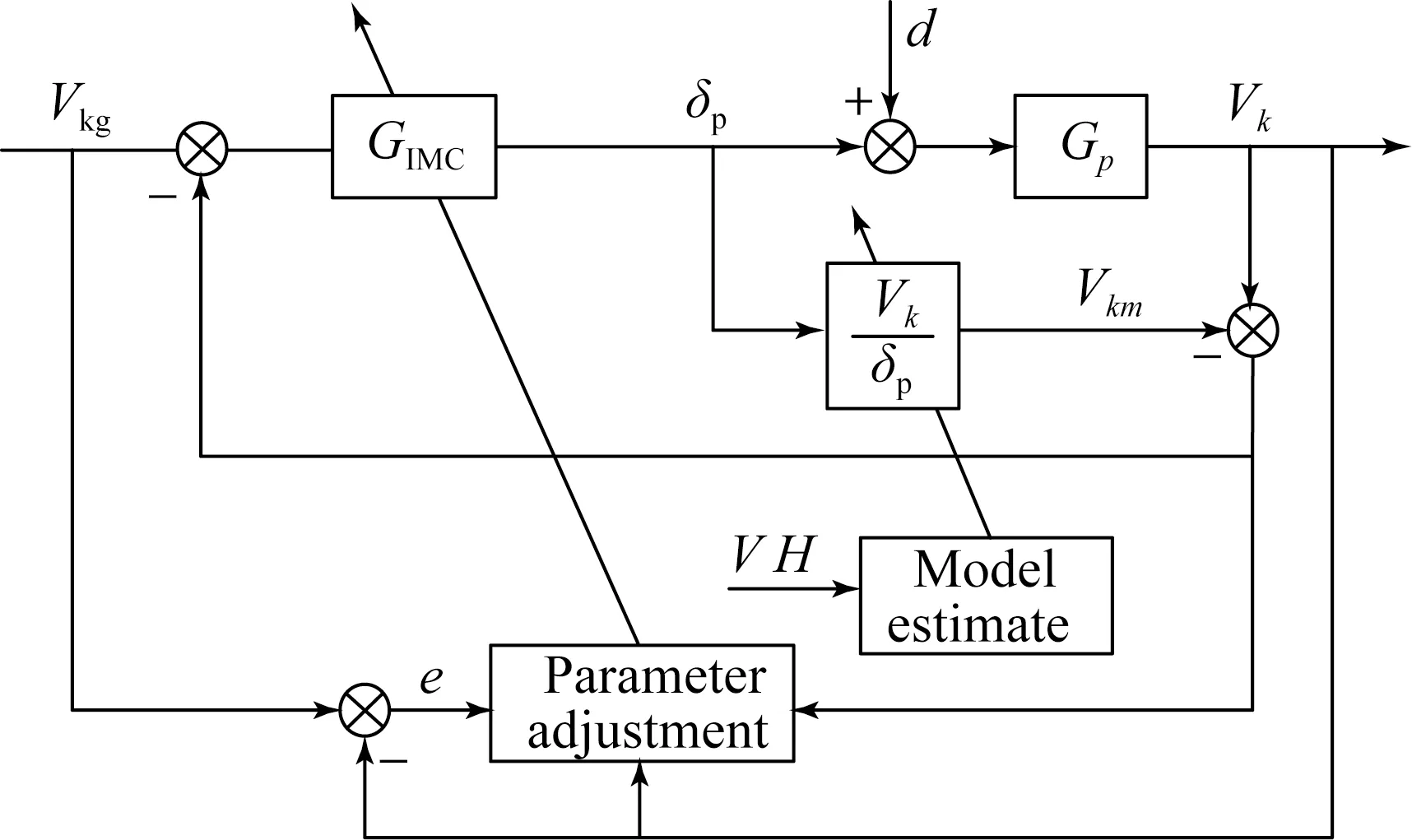
圖3　地速控制結(jié)構(gòu)

當(dāng)?shù)厮僬`差e大于1時(shí)，內(nèi)模濾波參數(shù)ε=ε0=0.5，當(dāng)?shù)厮僬`差e小于1時(shí)，采用式(4)對(duì)內(nèi)模濾波參數(shù)ε進(jìn)行調(diào)整。

2.4下沉率控制

通過(guò)高度指令對(duì)下沉率進(jìn)行控制，其控制結(jié)構(gòu)如圖4所示。

高度指令為：

Hg=H0-Vzg(t-t0)，

(9)

其中：H0為進(jìn)入下滑階段的起始高度，Vzg為設(shè)定下沉率，t0為進(jìn)入下滑階段的起始時(shí)間。

圖4下沉率控制結(jié)構(gòu)

Fig.4Structure of sink rate control

俯仰角速率作為下沉率控制的內(nèi)環(huán)控制目標(biāo)，應(yīng)用自適應(yīng)內(nèi)模原理進(jìn)行控制器設(shè)計(jì)。根據(jù)空速和高度的不同在模型估計(jì)器中調(diào)用相應(yīng)的氣動(dòng)參數(shù)形成反映俯仰角速率與升降舵關(guān)系的過(guò)程模型。當(dāng)俯仰角速率誤差e大于5時(shí)，內(nèi)模濾波參數(shù)ε=ε0=0.2，當(dāng)?shù)厮僬`差e小于5時(shí)，采用式(1)對(duì)內(nèi)模濾波參數(shù)ε進(jìn)行調(diào)整。

自適應(yīng)內(nèi)模控制器為無(wú)穩(wěn)差控制，因此將俯仰角和高度依次作為次外環(huán)和外環(huán)控制目標(biāo)，根據(jù)系統(tǒng)帶寬和最佳阻尼比等性能要求，進(jìn)行PID控制參數(shù)的選擇，其選擇參考值為Cθ=1.6，CH=2。

3　非線性數(shù)字仿真

自主著陸的標(biāo)稱航跡規(guī)劃如圖5所示，自主著陸過(guò)程由進(jìn)場(chǎng)飛行、陡下滑、淺下滑和接地減速滑停4部分組成。進(jìn)場(chǎng)飛行環(huán)節(jié)是無(wú)人機(jī)對(duì)準(zhǔn)航路，準(zhǔn)備進(jìn)入下滑線的預(yù)備環(huán)節(jié)。此時(shí)無(wú)人機(jī)離開(kāi)任務(wù)飛行，降低高度，進(jìn)入預(yù)定的起始下滑高度后轉(zhuǎn)入平飛，待姿態(tài)、高度和速度穩(wěn)定后便可以捕獲下滑軌跡準(zhǔn)備下滑。

著陸指標(biāo)設(shè)計(jì)如表2所示。

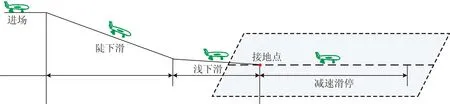
圖5　自主著陸航跡規(guī)劃

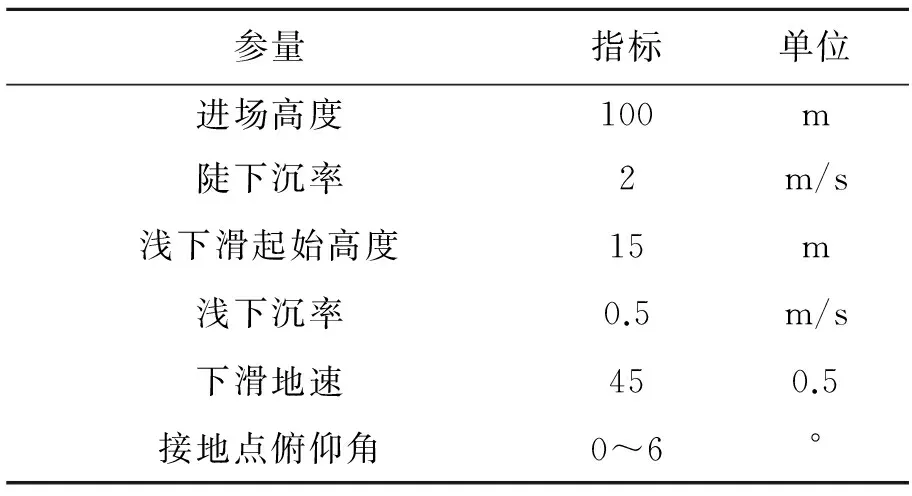
參量指標(biāo)單位進(jìn)場(chǎng)高度100m陡下沉率2m/s淺下滑起始高度15m淺下沉率0.5m/s下滑地速450.5接地點(diǎn)俯仰角0～6°

系統(tǒng)非線性數(shù)字仿真是檢驗(yàn)控制律設(shè)計(jì)有效性的通用方法，本文將常規(guī)IMC與AIMC系統(tǒng)仿真結(jié)果進(jìn)行了對(duì)比。對(duì)于本文控制系統(tǒng)，著陸仿真從進(jìn)入下滑開(kāi)始，著陸飛行接地為止。仿真初始位置設(shè)置為(-3 231，5，100)，初始地速為45 m/s。分別在無(wú)風(fēng)、順風(fēng)(風(fēng)速為6 m/s)和逆風(fēng)(風(fēng)速為6 m/s)的條件下進(jìn)行仿真，其飛行狀態(tài)對(duì)比如圖6～8 所示。

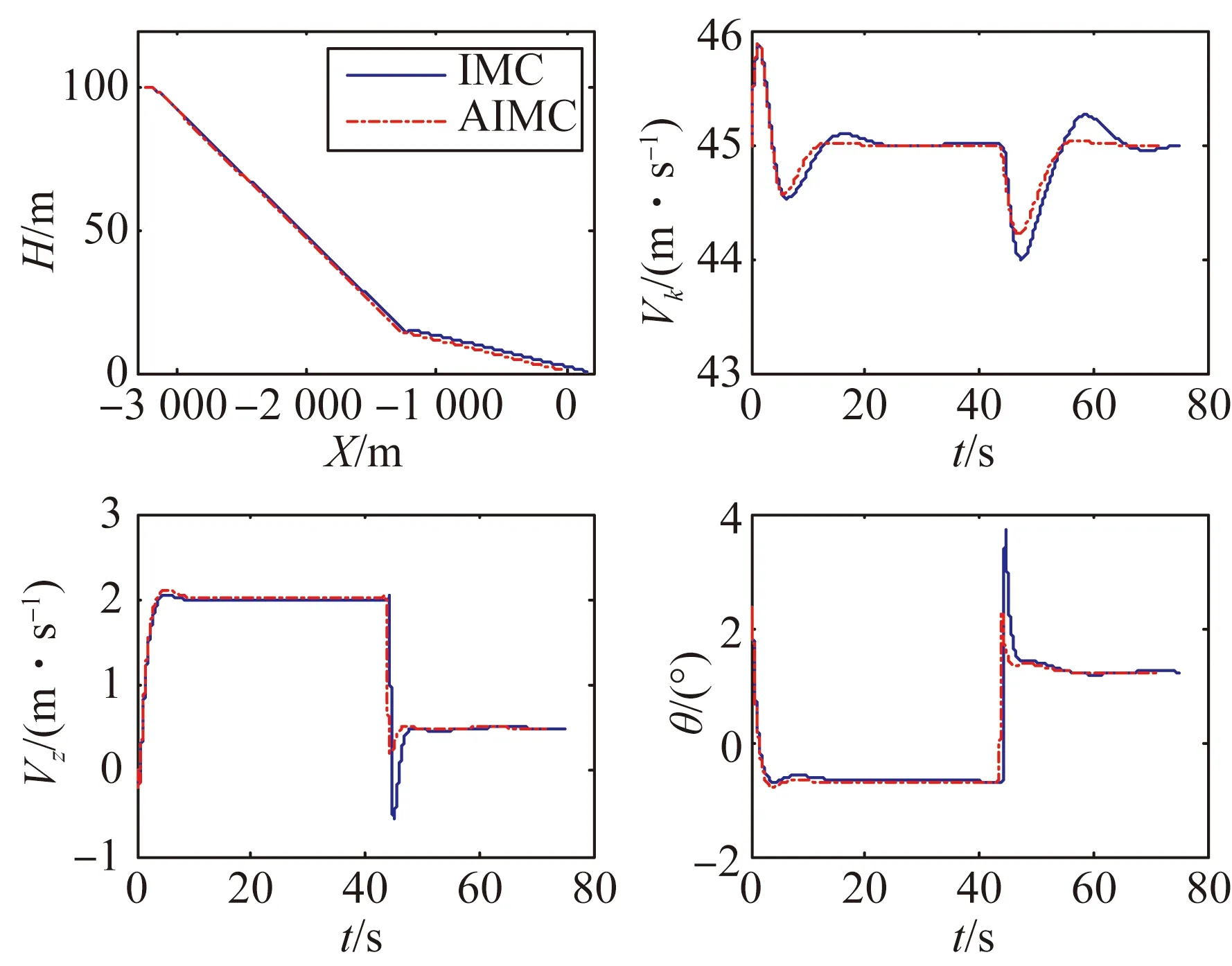
圖6　無(wú)風(fēng)著陸飛行狀態(tài)

在無(wú)風(fēng)條件下，AIMC系統(tǒng)著陸理想坐標(biāo)約為(0，0，0.6)，IMC系統(tǒng)的著陸理想坐標(biāo)約為(115，0，0.6)，當(dāng)飛行指令切入或改變時(shí)，AIMC系統(tǒng)飛行狀態(tài)抖動(dòng)較小，控制效果優(yōu)于IMC系統(tǒng)。

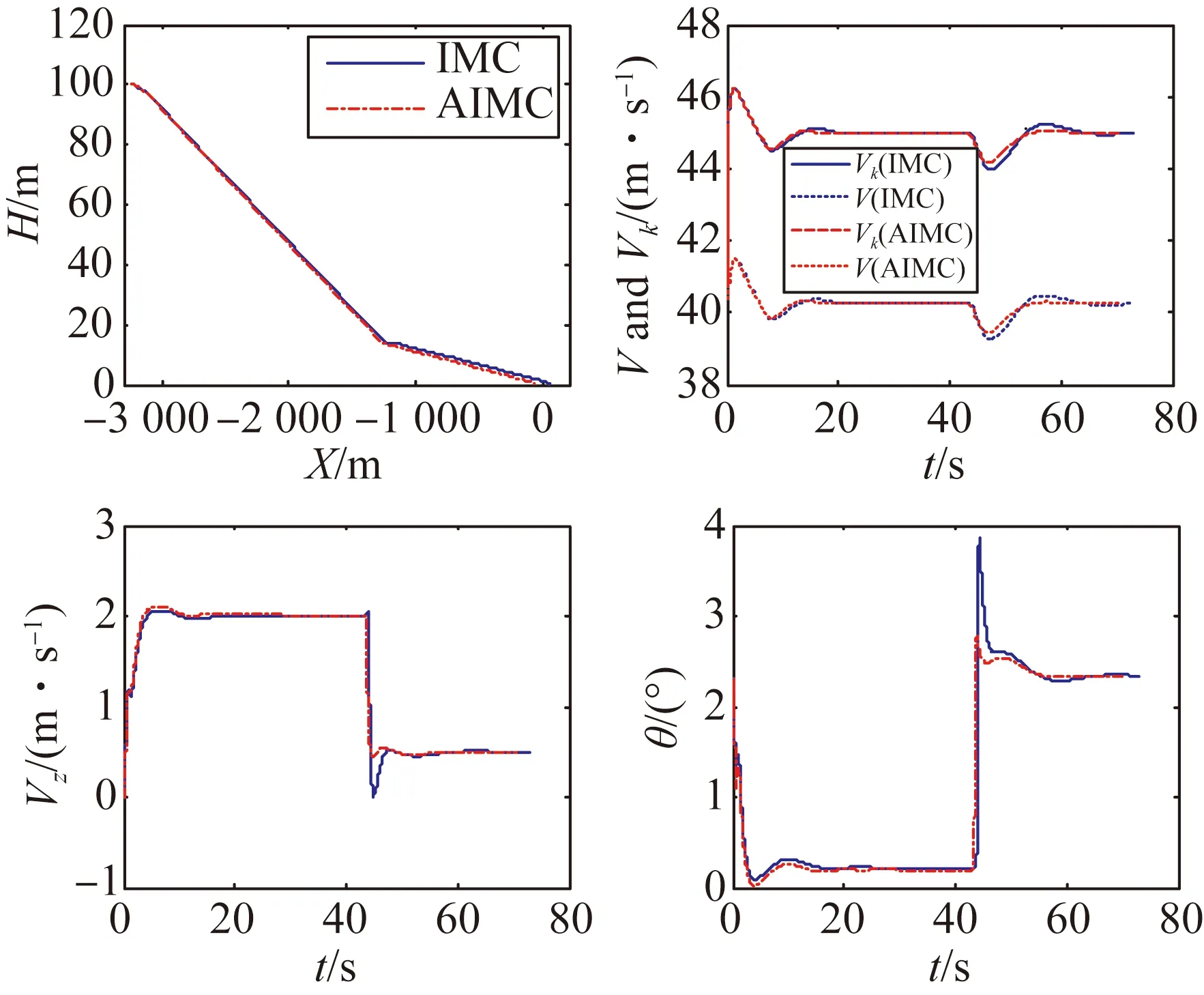
圖7　順向風(fēng)場(chǎng)著陸飛行狀態(tài)

在順風(fēng)(6 m/s)的條件下，飛行著陸點(diǎn)都位于理想著陸點(diǎn)后方，AIMC系統(tǒng)的著陸點(diǎn)在理想著陸點(diǎn)后方27 m，IMC系統(tǒng)的著陸點(diǎn)在理想著陸點(diǎn)后方102 m，上述實(shí)驗(yàn)結(jié)果顯示，在順風(fēng)情況下，AIMC系統(tǒng)動(dòng)態(tài)性能與著陸精度均明顯優(yōu)于IMC系統(tǒng)。

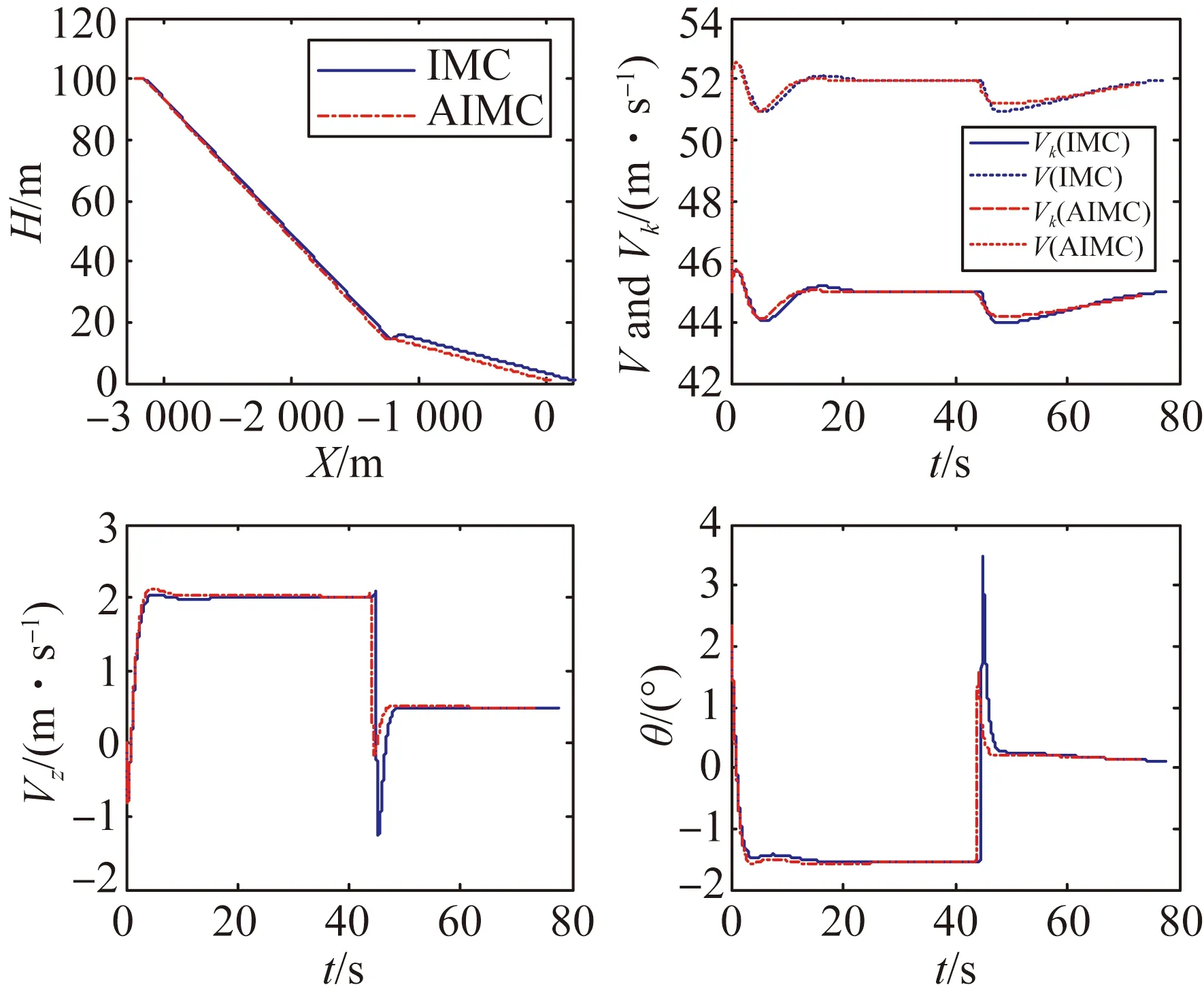
圖8　逆?zhèn)认蝻L(fēng)場(chǎng)著陸飛行狀態(tài)

在逆風(fēng)(6 m/s)的條件下，兩種方法的行著陸點(diǎn)均位于理想著陸點(diǎn)前方，AIMC系統(tǒng)的著陸點(diǎn)在理想著陸點(diǎn)前方25 m，IMC系統(tǒng)的著陸點(diǎn)在理想著陸點(diǎn)前方82 m，實(shí)驗(yàn)結(jié)果顯示，AIMC系統(tǒng)的動(dòng)態(tài)性能和著陸精度均明顯優(yōu)于IMC系統(tǒng)。

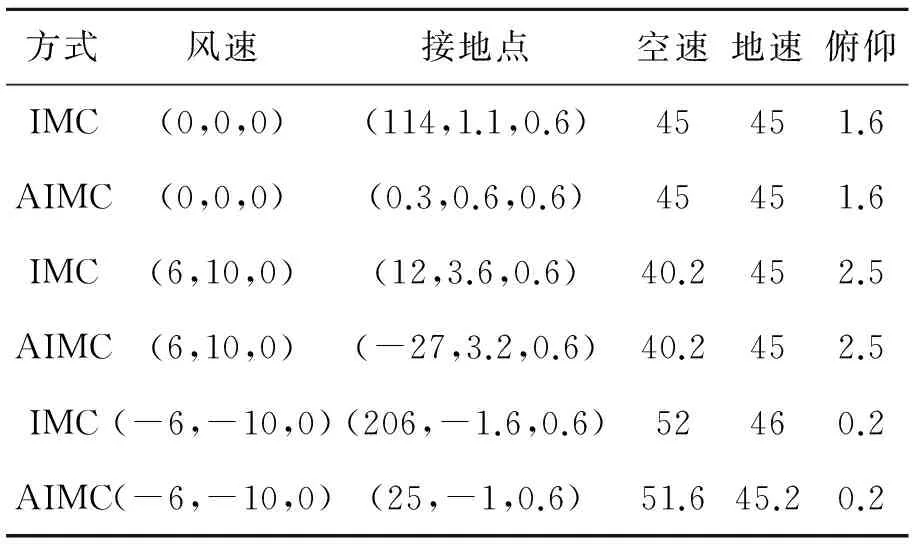
表3　接地點(diǎn)飛行狀態(tài)

在不同風(fēng)場(chǎng)條件下，不同控制方式的自主著陸接地點(diǎn)的飛行狀態(tài)對(duì)比結(jié)果如表3所示。從表中可以看出，常規(guī)IMC與AIMC系統(tǒng)均能實(shí)現(xiàn)對(duì)地速、高度和側(cè)偏距的穩(wěn)態(tài)控制，但AIMC系統(tǒng)動(dòng)態(tài)響應(yīng)過(guò)程明顯優(yōu)于PID控制系統(tǒng)，而動(dòng)態(tài)響應(yīng)過(guò)程將直接影響著陸點(diǎn)的精度，因此，在相同條件下，AIMC系統(tǒng)的著陸精度要優(yōu)于PID控制系統(tǒng)。

4　半物理測(cè)試

半物理測(cè)試原理及平臺(tái)搭建分別如圖9～10所示。

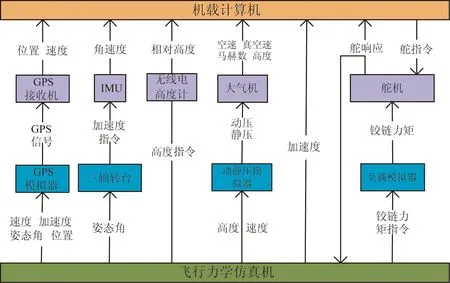
圖9　半物理測(cè)試原理圖

實(shí)驗(yàn)中，由飛行動(dòng)力學(xué)仿真機(jī)實(shí)時(shí)記錄飛行狀態(tài)，GPS模擬器接收仿真機(jī)輸出的地速、加速度、姿態(tài)及位置來(lái)模擬GPS信號(hào)，再由GPS接收機(jī)解算出地速和位置。三軸轉(zhuǎn)臺(tái)接收仿真機(jī)輸出的姿態(tài)角驅(qū)動(dòng)轉(zhuǎn)臺(tái)轉(zhuǎn)動(dòng)，安裝在轉(zhuǎn)臺(tái)上的INS隨轉(zhuǎn)臺(tái)一同轉(zhuǎn)動(dòng)，模擬機(jī)體的角運(yùn)動(dòng)。利用動(dòng)靜壓模擬器接收仿真機(jī)輸出的速度和高度，以模擬相應(yīng)的動(dòng)靜壓，利用大氣機(jī)接收動(dòng)靜壓信號(hào)，并解算出空速、真空速、馬赫數(shù)和氣壓高度。負(fù)載模擬器用以接收仿真機(jī)解算的鉸鏈力矩指令來(lái)模擬舵面產(chǎn)生的鉸鏈力矩。機(jī)載計(jì)算機(jī)接收到上述全部信息后，解算出相應(yīng)的控制律，并輸出舵指令給舵系統(tǒng)，舵系統(tǒng)將采集到的舵響應(yīng)給機(jī)載計(jì)算機(jī)和動(dòng)力學(xué)仿真機(jī)，用以計(jì)算控制律和飛行參數(shù)，從而形成整個(gè)閉環(huán)系統(tǒng)。

圖10　半物理測(cè)試平臺(tái)

半物理測(cè)試條件設(shè)定為無(wú)風(fēng)，初始位置坐標(biāo)為(-3 231，5，100)，初始地速為45 m/s，實(shí)驗(yàn)結(jié)果如圖11～12所示。

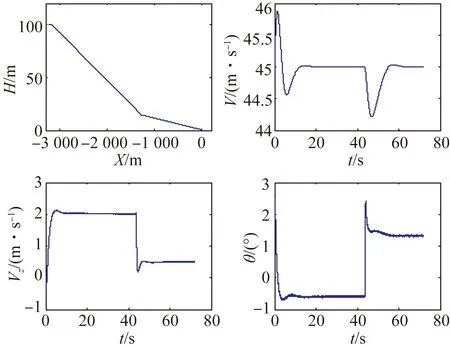
圖11 半物理測(cè)試飛行狀態(tài)

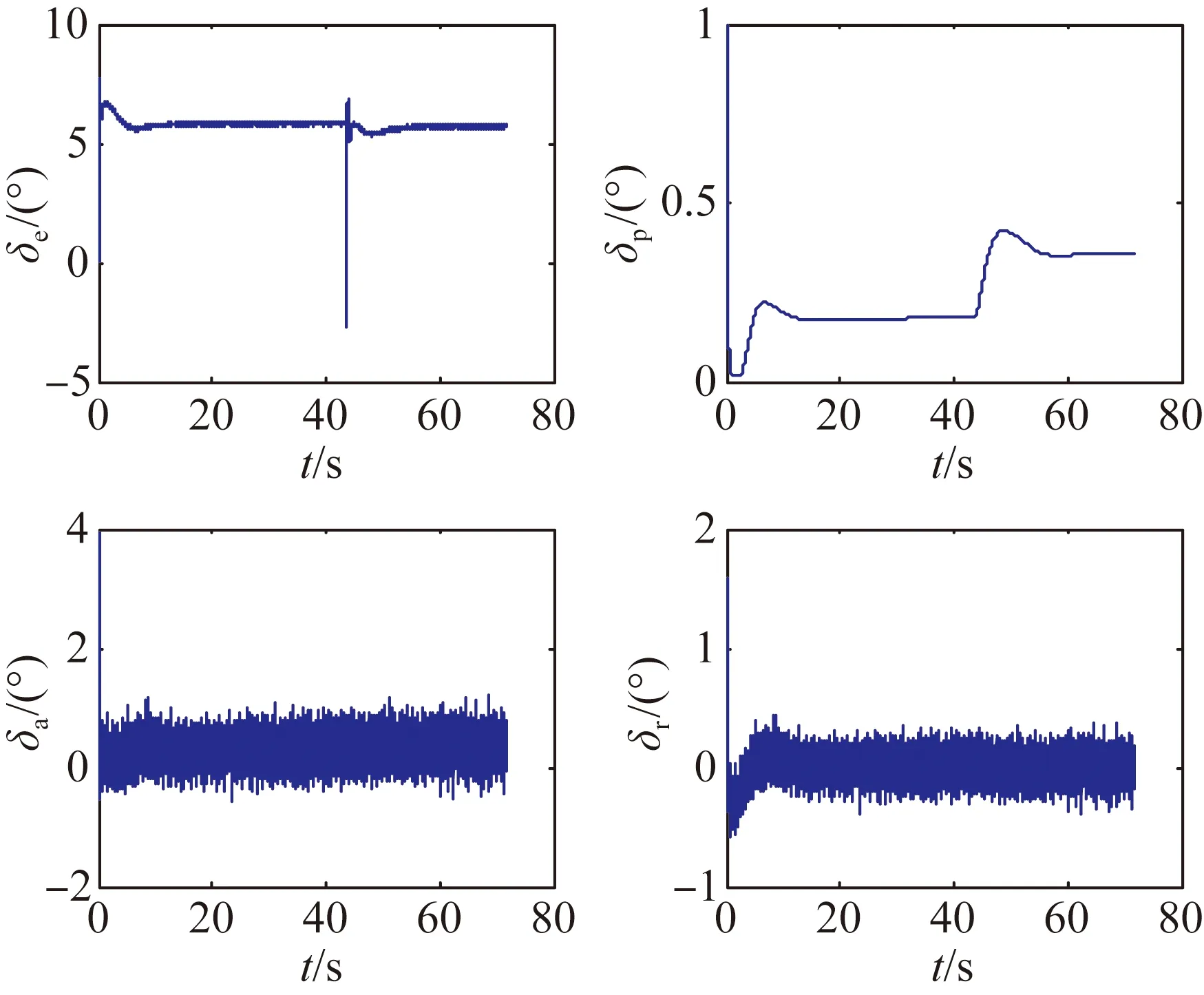
圖12　半物理測(cè)試舵反饋

半物理測(cè)試接地點(diǎn)坐標(biāo)為(1.8，0.9，0.6)，接地俯仰角為1.2°，接地速度為45 m/s，接地下沉率為0.5 m/s，且整個(gè)著陸過(guò)程中，控制指令切入或改變時(shí)，飛行狀態(tài)抖動(dòng)較小。將半物理測(cè)試結(jié)果分別和數(shù)字仿真結(jié)果圖6相比較可見(jiàn)，二者響應(yīng)基本一致，半物理測(cè)試復(fù)現(xiàn)了數(shù)字仿真結(jié)果，但半物理測(cè)試相對(duì)于系統(tǒng)數(shù)字仿真結(jié)果具有一定的噪聲，這是由于實(shí)際舵系統(tǒng)及整個(gè)傳感器系統(tǒng)產(chǎn)生的。

5　結(jié)　論

本文以無(wú)人機(jī)自主高精度定點(diǎn)著陸為目標(biāo)，應(yīng)用自適應(yīng)內(nèi)模控制原理設(shè)計(jì)了自主著陸縱向飛行控制律。自適應(yīng)內(nèi)模控制器濾波參數(shù)可自調(diào)整；從而改善了系統(tǒng)的動(dòng)態(tài)特性，引入模型辨識(shí)增強(qiáng)了系統(tǒng)的魯棒性。數(shù)字仿真在順逆風(fēng)場(chǎng)6 m/s的條件下，落點(diǎn)精度在理想落點(diǎn)30 m范圍內(nèi)，與傳統(tǒng)IMC系統(tǒng)相比較，AIMC系統(tǒng)在動(dòng)態(tài)性能和落點(diǎn)精度等方面均有明顯提高。最后搭建半物理測(cè)試平臺(tái)，且通過(guò)半物理測(cè)試復(fù)現(xiàn)了數(shù)字仿真的結(jié)果，并驗(yàn)證了系統(tǒng)的完整性與協(xié)調(diào)性，為無(wú)人機(jī)自主著陸飛行試驗(yàn)提供了基礎(chǔ)和保證。

[1]宋輝. 復(fù)雜條件下無(wú)人機(jī)自動(dòng)著陸控制技術(shù)研究[D]. 南京：南京航空航天大學(xué)， 2011.

SONG H.ResearchonautomaticlandingcontroltechnologiesforUAVundercomplexconditions[D]. Nanjing： Nanjing University of Aeronautics and Astronautics， 2011.(in Chinese)

[2]車軍， 張新國(guó).自動(dòng)著陸精確軌跡跟蹤控制[J].北京航空航天大學(xué)學(xué)報(bào)， 2005， 9(31)： 975-979.

CHE J， ZHANG X G. Exact trajectory tracking control of automatic landing [J].JournalofBeijingUniversityofAeronauticsandAstronautics， 2005， 9(31)： 975-979.(in Chinese)

[3]張建宏，張平.無(wú)人機(jī)自主精確著陸控制律設(shè)計(jì)及仿真研究[J].系統(tǒng)仿真學(xué)報(bào)， 2009， 21(3)： 743-748.ZHANG J H， ZHANG P. Autonomous precise landing control law for UAV [J].JournalofSystemSimulation， 2009， 21(3)： 743-748.(in Chinese)[4]AGUSTIN G M， RODOLFO E， HABER G. Internal mode control based on neuro fuzzy system for network application [J].IEEETransactionsonAutomaticsScienceandEngineering， 2009， 6(2)： 367-372.

[5]郭艷艷，陳瀾，楊常偉. 無(wú)人機(jī)著陸抗風(fēng)魯棒H∞控制器設(shè)計(jì)研究[J]. 計(jì)算機(jī)測(cè)量與控制， 2010， 21(2)： 348-350.

GUO Y Y， CHEN L， YANG CH W. Design of a robustH∞controller for UAV automatic landing under wind shear [J].ComputerMeasurement&Control， 2010， 21(2)： 348-350.(in Chinese)

[6]JIAQ L， WANG X M. Design of a robustH∞controller for automatic landing system of an aircraft [J].FlightDynamics， 2003， 21(1)： 32-35.

[7]SIEBERLING S， CHU Q P， MULDER J A. Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction [J].JournalofGuidance，ControlandDynamics， 2010， 33(6)： 1732-1742.

[8]陳華坤，章衛(wèi)國(guó)，王新民. 艦載機(jī)縱向自動(dòng)著艦控制系統(tǒng)設(shè)計(jì)[J]. 彈箭與制導(dǎo)學(xué)報(bào)， 2007， 27(1)： 73-77.CHEN H K， ZHANG W G， WANG X M. Design of automatic control system for longitudian landing on carrier [J].Journalofprojectiles，rockets，missilesandguidance， 2007， 27(1)： 73-77.(in Chinese)

[9]段鎮(zhèn)， 高九州. 無(wú)人機(jī)滑跑線性化建模與增益調(diào)節(jié)糾偏控制[J]. 光學(xué) 精密工程， 2014， 22(6)：1507-1516.DUAN ZH， GAO J ZH.Linearized modeling and gain scheduling control for UAV taxiing [J].Opt.PrecisionEng.， 2014， 22(6)：1507-1516.(in Chinese)

[10]李迪， 陳向堅(jiān)， 續(xù)志軍. 增益自適應(yīng)滑模控制器在微型飛行器飛行姿態(tài)控制中的應(yīng)用[J].光學(xué) 精密工程， 2013， 21(5)：1183-1192.

LI D， CHEN X J， XU ZH J. Gain adaptive sliding mode controller for flight attitude control MAV [J].Opt.PrecisionEeg.， 2013， 21(5)：1183-1192.(in Chinese)

[11]王洋， 張京娟. 基于自適應(yīng)控制的無(wú)人機(jī)飛行控制系統(tǒng)研究[J]. 彈箭與制導(dǎo)學(xué)報(bào)， 2010， 30(4)： 15-19.

WANG Y， ZHANG J J. Research on flight control system based adaptive controller for UAV [J].JournalofProjectiles，Rockets，MissilesandGuidance， 2010， 30(4)： 15-19.(in Chinese)

[12]ALCANTARA S， PEDRET C， VILANOVA R，etal.. Generalized internal model control for balancing input/output disturbance response [J].IndEngChemRes.， 2011， 50(19)： 70-80.

[13]蔡紅明， 昂海松， 鄭祥明. 基于自適應(yīng)逆的微型飛行器飛行控制系統(tǒng)[J]. 南京航天航空大學(xué)學(xué)報(bào)， 2011， 43(2)： 137-142.

CAI H M， ANG H S， ZHENG X M. Flight control system of MAV based on adaptive dynamic inversion [J].JournalofNanjingUniversityofAeronauticsandAstronautics， 2011， 43(2)： 137-142.(in Chinese)

[14]李艷輝， 歷明， 周凌. 基于模型匹配的光電偵查無(wú)人機(jī)飛行控制器設(shè)計(jì)方法[J]. 紅外與激光工程， 2015，44(2)： 693-670.LI Y H， LI M， ZHOU L. UAV flight controller design method based on model matching used for electro-optical reconnaissance[J].InfraredandLaserEngineering， 2015，44(2)： 693-670.(in Chinese)

[15]吳德偉，胡奕明. 無(wú)人機(jī)自主著陸半實(shí)物仿真系統(tǒng)設(shè)計(jì)[J]. 系統(tǒng)仿真學(xué)報(bào)， 2008， 20(24)： 6815-6820.

WU D W， HU Y M. Design of hardware-in-the-loop simulation system to UAV automatic landing guidance[J].JournalofSimulation， 2008， 20(24)： 6815-6820.(in Chinese)

高九州(1987-)，男，遼寧本溪人，博士研究生，2006年、2010年于哈爾濱工業(yè)大學(xué)分別獲得學(xué)士、碩士學(xué)位，主要從事飛行力學(xué)與控制等方面的研究。E-mail： gaojiuzhou@126.com

導(dǎo)師簡(jiǎn)介：

賈宏光(1971-)，黑龍江五常人，研究員，博士生導(dǎo)師，1994年于哈爾濱工業(yè)大學(xué)獲得學(xué)士學(xué)位，1997年于長(zhǎng)春光機(jī)學(xué)院獲得碩士學(xué)位，2000年于中國(guó)科學(xué)院長(zhǎng)春光學(xué)精密機(jī)械與物理研究獲得博士學(xué)位，主要從事復(fù)合制導(dǎo)與目標(biāo)識(shí)別等方面的研究。E-mail： jiahg@ciomp..ac.cn

(版權(quán)所有未經(jīng)許可不得轉(zhuǎn)載)

Design of longitudinal control law for small fixed-wing UAV during auto landing

GAO Jiu-zhou1，2*， JIA Hong-guang1

(1.ChangchunInstituteofOptics，F(xiàn)ineMechanicsandPhysics，ChineseAcademyofSciences，Changchun130033，China；2.UniversityofChineseAcademyofSciences，Beijing100039，China)

*Correspondingauthor，E-mail：gaojiuzhou@126.com

For the auto landing precisely of an Unmanned Aerial Vehicle(UAV), the longitudinal control law for the auto landing of the UVA was designed based on Adaptive Internal Model Control (AIMC) principle. By taking a small wheeled UVA as a working platform, the longitudinal nonlinear model was decoupled and linearized. Then, the ground speed and sink rate were selected as control targets and longitudinal control law was designed based on the AIMC and applied to control system design. The filter parameter was adjusted to improve the dynamic characteristics of the system and the model was identified to enhanced the robustness of the system. The AIMC system was simulated digitally under the conditions of ownwind or headwind in a speed of 6 m/s, and the results show that the landing precision of system is in a scope of 30 m for forward or backward directions. Finally, a hardware test platform was established to verify the simulation results and the hardware-in-loop-simulation (HILS) proves the harmony and integrality of the system.

Unmanned Aerial Vehicle(UAV); auto landing； Adaptive Internal Model Control(AIMC)； longitudinal control law； digital simulation； Hardware in Loop Simulation(HILS)

2015-12-15；

2016-01-12.

中國(guó)科學(xué)院三期知識(shí)創(chuàng)新工程(No.YYJ-1122)

1004-924X(2016)07-1799-08

V249.1

Adoi:10.3788/OPE.20162407.1799