基于彈性動力學的制動夾鉗結構剛度設計

曾梁彬　金　璟

（中車戚墅堰機車車輛工藝研究所有限公司，常州 213000）

基于彈性動力學的制動夾鉗結構剛度設計

曾梁彬金璟

（中車戚墅堰機車車輛工藝研究所有限公司，常州 213000）

針對制動夾鉗結構剛度的設計，利用彈性動力學方法建立了一個6單元21自由度的有限元分析模型，通過求解系統運動微分方程，研究制動夾鉗各部分結構對系統整體剛度的影響情況，以期為夾鉗本體的結構設計提供理論依據。

制動夾鉗 結構剛度 彈性動力學

1　引言

制動系統作為動車組九大關鍵技術之一，其性能直接影響列車運行的安全。對于基礎制動裝置中的制動夾鉗而言，若其結構剛度設計不足，將可能導致多方面的功能性與安全性問題。一方面可能引起夾緊力曲線出現遲滯；另一方面，在高制動載荷狀態下，制動缸間隙調整機構的端齒配合可能會出現“跳齒”現象，使得緩解后盤片間隙減小。此外，過大的結構形變也會造成關鍵承載件的疲勞壽命縮短。

針對上述問題，本文利用彈性動力學方法，研究制動夾鉗本體關鍵承載件的結構設計對整體剛性的影響，并對其截面設計提供理論依據。

2　彈性動力學建模

2.1制動夾鉗簡化模型

圖1所示為動車組用三點吊掛制動夾鉗單元的一般結構，主要由夾鉗本體和制動缸兩部分組成。其中，夾鉗本體中最主要的承載構件為吊架和杠桿。因此，本文的結構剛度設計重點圍繞杠桿和吊架展開。

圖1　制動夾鉗單元

本文采用有限元模型來簡化杠桿吊架連續體模型。根據文獻[1]對單元長度的規定，將杠桿和吊架用2個單元來模擬，以保證較小的計算誤差。整個制動夾鉗杠桿吊架模型可簡化為一個6單元7節點的有限元模型，如圖2所示。

圖2　制動夾鉗杠桿吊架簡化有限元模型

2.2系統運動微分方程

2.2.1梁單元及單元廣義坐標

根據制動夾鉗結構特點，采用等截面直線梁單元來模擬杠桿和吊架各部分結構[2]。梁單元模型及各坐標系如圖3所示。

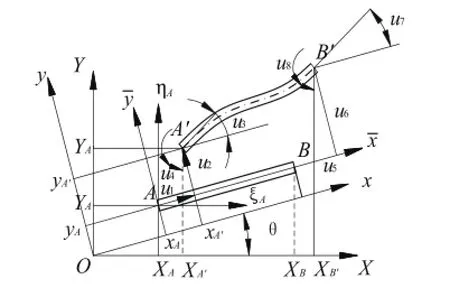
圖3　梁單元模型及坐標關系

梁單元上任意點縱向（x方向）和橫向（y方向）位移分別用W（,t）和V（,t）表示

設u1（t）、u5（t）分別為節點A、B的縱向位移；u2（t）、u6（t）分別為節點A、B的橫向位移；u3（t）、u7（t）分別為節點A、B的彈性轉角；u4（t）、u8（t）分別為節點A、B的曲率。

于是，梁單元的單元廣義坐標向量為

其邊界條件為

將式（3）代入式（1），于是

通過坐標變換可將絕對參考坐標系下的絕對速度和加速度表示為旋轉坐標系下的形式，坐標變換如下：

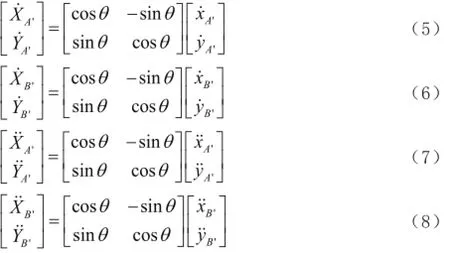
進而得到的速度和加速度關系為

2.2.2單元運動微分方程

梁單元能量主要包括動能與彈性變形能兩部分。單元動能可寫為

單元變形能可寫為

其中，

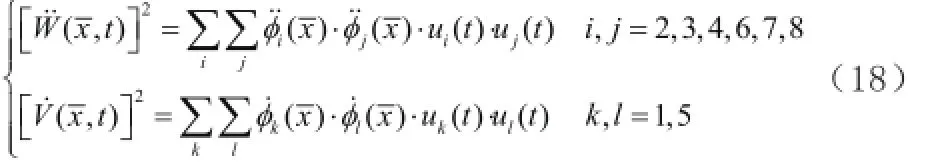
將式（18）代入式（17）得到

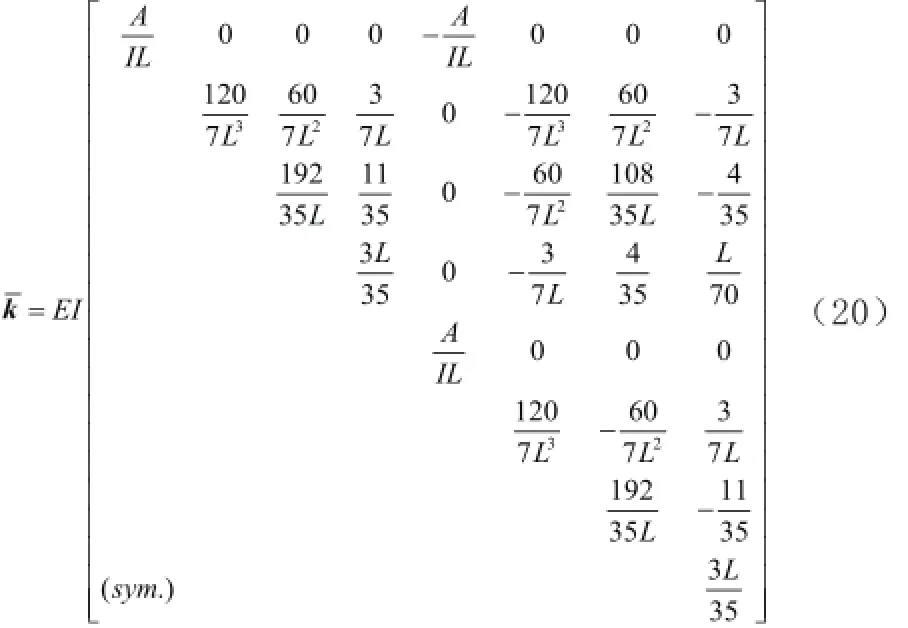
梁單元的拉格朗日方程可寫為

將式（19）對iu˙求導得到

將式（22）-（24）代入（21），并寫成矩陣形式

考慮式（12），則上式可改寫為

由此，得到旋轉坐標系下的單元運動微分方程。

以A點和B點為原點，分別建立平動坐標系A-ξAηA和B-ξBηB。設平動坐標系下的單元廣義坐標列陣為

則平動坐標系下的單元廣義坐標Ue與旋轉坐標系下廣義坐標u之間關系為

其中，R為坐標轉換矩陣

將式（26）左乘RT得到

其中，m和k分別為單元當量質量矩陣和單元當量剛度矩陣。

f為對應于廣義坐標Ue的廣義力列陣，其形式為

2.2.3系統運動微分方程

以制動夾鉗單元的實際工況作為邊界條件，將簡化模型設置為一個6單元7節點21自由度的有限元模型（自由度設置規則詳見文獻[3]）。各單元節點自由度設置及廣義坐標編號如圖2和表1所示。

表1　各單元節點自由度與廣義坐標編號

根據表1即可寫出系統的模型組成矩陣Iu。引入單元坐標協調矩陣Bi（i=1, 2, ..., 6），其形式為

進一步可獲得

其中，

將所有單元在廣義坐標系下的運動方程累加起來，即可得到系統的運動微分方程

其中，M、K和F分別為系統質量矩陣、系統剛度矩陣和系統廣義力列陣。若考慮阻尼，則系統運動微分方程為

3　動態響應求解

3.1固有頻率求解

制動夾鉗簡化模型的無阻尼自由振動方程為

其解為

其中，A為振幅列陣；ω為系統固有圓頻率；α為初始相位角。將式（45）代入（44），得到

求解上式即可獲得系統各階固有頻率。

3.2動態響應求解

3.2.1方程解耦

通過式（46）（47）可以得到系統的n個固有頻率和相應的主振型Ar（r=1, 2, ..., n）。設稱為正則化因子；φr稱為第r階正則振型且滿足以下條件其中，

對n階主振型均進行正則化處理后構成正則振型矩陣Φ

利用正則振型矩陣，則有

各階正則振型矢量φ1,φ2,...,φn線性無關，可以作為n維線性空間的一組基底。將系統廣義坐標矢量U表示為

其中

系統無阻尼自由振動方程即可轉變為

因此，式（54）可以展開為n個互不耦合的獨立方程

3.2.2正則振型阻尼假定

將阻尼矩陣假定為系統質量矩陣和剛度矩陣的線性組合

式中的α和β為常數。設

其中ζ1,ζ2,...,ζn稱為振型阻尼比。則系統自由振動方程轉化為

在阻尼比較小的情況下（0≤ζi≤0.2），采用該振型阻尼假設時分析產生的誤差較小。本文取各階正則阻尼比均為0.05。

3.2.3廣義力矩陣定義

制動夾鉗主要承受來自制動缸的推力，其作用在兩側杠桿后端。在簡化模型中，制動缸推力施加在廣義坐標u16和u19上。考慮廣義力列陣F后，可得到正則化后的系統有阻尼受迫振動方程

其中

4　制動夾鉗剛度設計算例

由于制動夾鉗主要變形集中在杠桿后半部分，所以本文采用杠桿后端節點的位移來衡量制動夾鉗整體結構剛度，即廣義坐標u16和u19。

以某制動夾鉗結構為例，材料為QT600-7，密度7120kg/m3，彈性模量169GPa。各單元的長度、截面積與慣性矩見表2。將各參數代入上述模型，設制動缸推力10kN，可以計算得到廣義坐標u16和u19處的位移約為1.057mm。

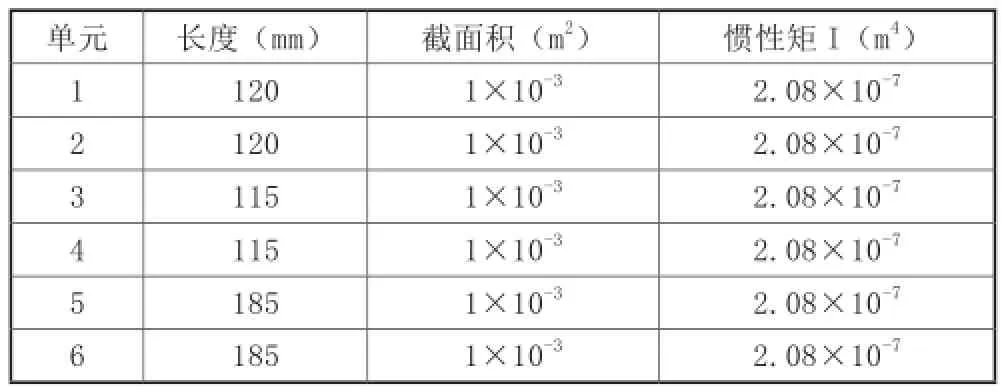
表2　各單元結構參數

分別以單元1和2、單元3和4、單元5和6的截面慣性矩為變量，得到各單元截面慣性矩對最大變形量的敏感度，如圖4所示。

圖4　各單元界面慣性矩對最大變形的影響

從圖4中可以看出，單元5和6對最大變形的敏感度最高，其次為單元1和2，單元3和4最低。由此可知，增大杠桿后半部分的截面慣性矩對改善夾鉗整體剛性和降低變形效果最為明顯。

5　結論

（1）文中采用等截面直線梁單元對制動夾鉗關鍵承載件進行模擬，建立了系統運動微分方程，能夠直接獲得外部載荷與結構變形之間的關系。

（2）通過算例，對比制動夾鉗各部分結構對整體結構剛度的影響。其中，通過增大杠桿后半部分的截面慣性矩對改善整體結構剛度效果最明顯。因此，結構設計中可優先對該部分進行優化。

（3）文中所采用的6單元21自由度簡化模型，能夠用于指導對吊架、左右杠桿前半部和后半部進行等截面設計。利用相同方法將夾鉗本體進一步拓展為多單元多自由度模型，則能夠對變截面杠桿吊架的結構設計提供理論依據。

[1]王生澤，廖道訓.高速平面連桿機構彈性變形及動應力的有限元分析[J].華中理工大學學報，1988，（3）：115-122.

[2]張策.機構動力學[M].北京：高等教育出版社，2008.

[3]曾梁彬.新型肘桿式高速壓力機關鍵技術研究[D].南京：南京理工大學，2012.

Structural Stiffness Design of Brake Caliper Bas ed on Elasto-Dynamic Analysis

ZENG Liangbin,JIN Jing
(CRRC Qishuyan Institute Co.,Ltd, Changzhou 213000)

A FE A model with 6 e lements a nd 21 DOFs, which was established by elasto-dynamic method, was introduced into structural s tiffness design of brake caliper. By s olving the system’s differential equation of motion, the influences of different parts of brake caliper on the structural stiffness of system were inves tigated, which will provide a theoretical basis for the structure design of brake caliper.

Brake caliper, Structural stiffness, Elastodynamic analysis