基于鄰接表結(jié)構(gòu)的拓撲排序的全序列算法研究

薛春艷

（廈門大學(xué)嘉庚學(xué)院信息科學(xué)與技術(shù)學(xué)院，廈門 361000）

基于鄰接表結(jié)構(gòu)的拓撲排序的全序列算法研究

薛春艷

（廈門大學(xué)嘉庚學(xué)院信息科學(xué)與技術(shù)學(xué)院，廈門 361000）

拓撲排序是有向無環(huán)圖的用來描述各活動間的先后關(guān)系的重要應(yīng)用。利用拓撲排序算法能得到圖中的各活動的線性序列，同時這個序列滿足各活動在圖中體現(xiàn)的先后關(guān)系，即拓撲序列。常用的求解拓撲排序方法是求得一個拓撲序列即可。為了增強算法的實用價值，給出求解有向無環(huán)圖的所有拓撲序列的方法，并討論算法的原理及代碼實現(xiàn)，驗證全拓撲排序算法的實用性和正確性。

拓撲排序；全序列；鄰接表

0 引言

有向無環(huán)圖在實際應(yīng)用中經(jīng)常用來描述工程或者系統(tǒng)的進行過程。如工程施工圖、學(xué)生選課關(guān)系圖等。在圖中，用頂點表示活動，用有向邊表示活動間的先后關(guān)系，這種有向圖稱為AOV網(wǎng)(Activity On Vertex Network)。將AOV網(wǎng)中的各個頂點排成一個線性序列，使各頂點在序列中保持其在圖中體現(xiàn)出來的先后關(guān)系，這個過程稱為拓撲排序。由此得到的線性序列稱為拓撲序列[1]。

求有向無環(huán)圖的拓撲序列的意義在于可以根據(jù)拓撲序列對圖中活動進行串行地安排，從而提高活動安排的效率。如學(xué)生課程間的安排、生產(chǎn)控制過程的優(yōu)化、工程施工的過程管理等[2]。

有向無環(huán)圖的拓撲序列通常情況下是不唯一的，常用的拓撲排序方法當(dāng)?shù)玫揭粋€拓撲序列后就結(jié)束了；在很多應(yīng)用中，只求出一個拓撲序列是不夠的，需要得到的該圖的全部可能的拓撲序列，再根據(jù)相關(guān)的要求選出最佳的拓撲序列。

1 拓撲排序算法的存儲結(jié)構(gòu)

在計算機中實現(xiàn)時，有向無環(huán)圖采用了鄰接表作為存儲結(jié)構(gòu)。同時在基本的鄰接表的基礎(chǔ)上進行了改進，為了實現(xiàn)算法的方便，在頂點結(jié)構(gòu)中加了一項，用來存放該頂點入度的值。通過這個入度的值可以進行下面兩操作：

（1）判斷當(dāng)前頂點是否是無前驅(qū)的頂點：即判斷其入度是否為0；

（2）輸出頂點后，需要刪除該頂點和所有以它為尾的弧的操作：即將以該頂點為弧尾的另一端的弧頭頂點的入度減1。

同時，需要設(shè)一個棧結(jié)構(gòu)來存放拓撲排序過程中所有入度為零的頂點[3]。改進后的有向無環(huán)圖的存儲結(jié)構(gòu)如下：

以圖1為例，圖2是圖1的鄰接表結(jié)構(gòu)示意圖。

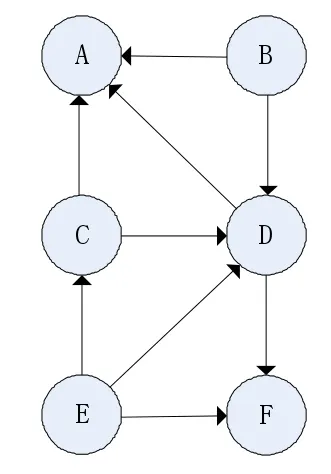
圖1 無向圖G

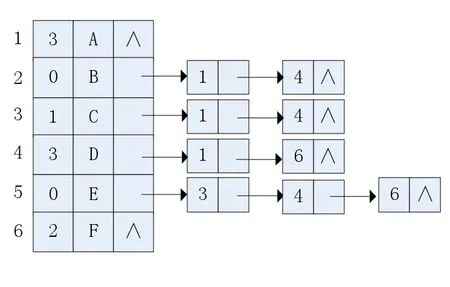
圖2 無向圖G的鄰接表示意圖

2 拓撲排序的算法思想

拓撲排序的算法思想是：

（1）在有向無環(huán)圖中任選一個沒有前驅(qū)的頂點（無前驅(qū)的頂點可能有多個）并且輸出。

（2）刪除該頂點以及所有由該頂點發(fā)出的弧。

重復(fù)上述兩步，直到圖中所有頂點全部輸出為止。

其偽代碼如下：

（1）棧S初始化；

（2）掃描頂點表，將所有無前驅(qū)的頂點入棧；

（3）當(dāng)棧S非空時循環(huán)

棧頂元素vj出棧；輸出vj；

頂點vj的各個鄰接點的入度減1，若間后入度為0，則將該頂點入棧S。

若所有的頂點都已輸出，就表明所輸出的序列即為所求的該有向無環(huán)圖的拓撲序列。

3 全拓撲排序算法的原理與實現(xiàn)[3]

全拓撲排序采用了鄰接表作為圖的存儲結(jié)構(gòu)，通過深度優(yōu)先搜索獲得序列，利用棧結(jié)構(gòu)存儲無前驅(qū)的頂點，利用隊列結(jié)構(gòu)存儲所有可能的待檢測的序列，利用窮舉法來判斷是否符合拓撲排序的要求，最終求出所有符合要求的解。

（1）統(tǒng)計所有入度為0的頂點，窮舉出由這些頂點開始所能構(gòu)造的所有可能的頂點序列；

（2）判斷當(dāng)前序列是否是合法的拓撲排序，如果是，則輸出該序列，轉(zhuǎn)（1）。

（3）否則轉(zhuǎn)（2），直到所有可能序列都完成檢測為止。

全拓撲排序函數(shù)代碼如下：

4 程序運行結(jié)果

根據(jù)圖1收入邊數(shù)：6和9條邊的信息（以“起點編號 重點編號”格式輸入），最終求得圖G的全拓撲序列為6個，具體情況如圖3所示。見圖3：

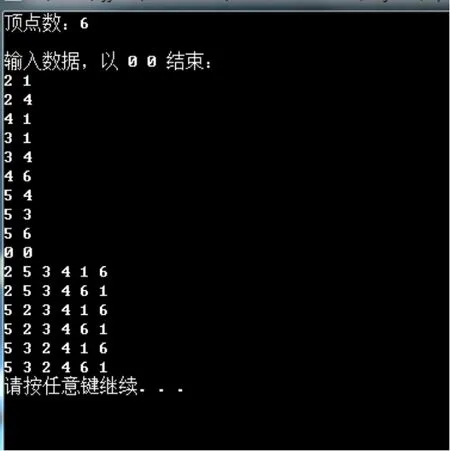
圖3 圖G的全拓撲序列求解結(jié)果

5 結(jié)語

本文給出了全拓撲序列算法的基本思想和具體編程實現(xiàn)過程。全拓撲排序算法思想簡單明了，時間復(fù)雜度和空間復(fù)雜度適當(dāng)。求解全拓撲排序目的是為了求解特殊條件下的最佳的拓撲序列。因此，若在獲得備選序列的過程中加上貪心規(guī)則，算法的性能還能得到進一步提高。

[1]嚴蔚敏，吳偉民.數(shù)據(jù)結(jié)構(gòu)（C語言版）[M].北京：清華大學(xué)出版社，1997.

[2]王瓊.拓撲排序算法的拓展研究[J].計算機工程與應(yīng)用，2006-24.

[3]朱立華，王汝傳.AOV網(wǎng)中全拓撲排序算法的設(shè)計及應(yīng)用[J].微機發(fā)展，2004-14.

Topology Sorting;All Sort;Adjacency List

Research on the Algorithm for all Topology Sorting Based on Adjacency List Structure

XUE Chun-yan
（College of Information Science and Technology,Xiamen University Tan Kah Kee College,Xiamen 361000）

Topology sort is an important application of a Directed Acyclic Graph for the relations between activities which in the DAG.Topology sort algorithm can get a linear sequence of each activity in this DAG,this sequence of activities meets all embodied relationship in the DAG, namely topological sequence.Usually,the topological sorting method obtains a topological sequence.In order to enhance the practical value of the algorithm,presents a method to get all the topology sequence of the DAG,and discusses the principle and the code algorithm, verifies the correctness and practicality of the full topological sorting algorithm.

1007-1423（2016）19-0074-03

10.3969/j.issn.1007-1423.2016.19.018

薛春艷（1976-），女，吉林遼源人，碩士研究生，副教授，研究方向為數(shù)字圖像處理、算法設(shè)計與分析、數(shù)據(jù)庫

2016-04-14

2016-07-02