海嘯波沿緩坡爬高試驗研究

張文忠，呂迎雪，劉鑫，黃宣軍（.中交天津港灣工程研究院有限公司，中國交建海岸工程水動力重點實驗室，天津　300；.深圳中廣核工程設計有限公司，廣東　深圳　5803）

海嘯波沿緩坡爬高試驗研究

張文忠1，呂迎雪1，劉鑫2，黃宣軍1
（1.中交天津港灣工程研究院有限公司，中國交建海岸工程水動力重點實驗室，天津300222；2.深圳中廣核工程設計有限公司，廣東深圳518031）

摘要：為了更好地評估海嘯波傳播到近岸后淹沒的范圍，通過在無反射造波水槽中產生孤立波模擬海嘯沿緩坡的傳播，分析海嘯波進入淺水區后變形的特性以及破碎的狀態，得到1頤15.3以及1頤30.12兩種坡度下的試驗數據，并且與有關學者提出的經驗公式進行比較，提出一個新的海嘯波沿緩坡最大爬高的經驗公式。計算成果表明，該經驗公式與大量的實測數據相關性良好。

關鍵詞：海嘯波；緩坡；爬高；經驗公式；物理模型試驗

0　引言

2011年3月11日下午，日本東部海域發生里氏9.0級大地震，并引發海嘯。福島第一核電站因受海嘯侵襲發生核泄漏事故，對人文、環境、經濟產生了災難性影響。由于我國沿海自然條件特點，以往國內對海嘯的關注和研究相對較少，對海嘯災害評估及岸線防護方面缺少資料和工程技術經驗。海嘯波本質上是一種長波，具有明顯的單一波峰形狀，其波高及水深相對于波長來說均為小值，屬于淺水長波。由于孤立波的波形與傳播特性與海嘯波類似，并且其波形函數簡單易于數學解析，因此常以孤立波模擬海嘯傳播變形。海嘯的模型試驗研究也隨著造波系統可以準確模擬孤立波而得到了發展，借由孤立波傳播的變形試驗為相關的數值模擬提供了重要的資料。

在孤立波的波形演化、最大爬坡高度以及破碎指標等相關研究方面，國內外學者已經做了很多相關工作，Hall&Watts[1]是實驗室中最早利用單一波峰的長波研究其傳播至傾斜的斜坡后波浪變形，這個試驗模擬的是海嘯在深海中傳播，而后爬上均勻斜坡的大陸架，通過量綱分析，得到波浪爬坡至斜坡上的最大爬坡高度R和外海波高H以及水深d和斜坡坡度β的關系。Synolakis[2]解決了利用非線性淺水方程求解孤立波爬坡的初值問題，并且推導出被后來學者普遍使用的非破碎孤立波爬高計算公式。關于破碎的孤立波爬高問題相關的試驗研究較少，Synolakis[2]根據1頤19.85的斜坡實驗結果得出適用于該坡度的最大爬坡高度經驗公式。Hsiao等人[3]在一個300 m伊5 m伊5.2 m的超大水槽中進行了大尺度的模型試驗，根據實驗結果利用最小二乘法歸納出坡度為60的破碎孤立波爬高經驗公式，而后又結合了Synolakis[4]等人的試驗數據得到了多種坡度的經驗公式。整體來看，現階段海嘯波沿緩坡最大爬高的經驗公式大多采用單一坡度的試驗數據進行擬合，Hsiao等人[3]雖然加入了部分前人數據，但是這些數據年代較早，試驗組次少，代表性較差。

為了使破碎后的海嘯波沿緩坡爬高公式適用的坡度及波高范圍更加廣泛，本文在前人工作的基礎上，在我國首臺引進的無反射造波斷面水槽中分別模擬1頤15.3和1頤30.12兩種坡度的緩坡地形，利用無反射造波機以二階孤立波為目標波形，進行了孤立波沿緩坡傳播試驗，得到了不同水深波高工況下海嘯波沿緩坡的爬高數據，并將試驗結果與Synolakis[2]的經驗公式及Hsiao等人[3]爬高公式進行了對比，而后又根據部分前人的試驗數據以及本文最新得到的數據利用最小二乘法得到了一個改進的新的海嘯波沿緩坡爬高的經驗公式，使得本次擬合的經驗公式坡度范圍在15～60，波高水深比范圍在0.01～0.633。

1　物理模型試驗介紹

海嘯波斷面物理模型試驗是在中交天津港灣工程研究院有限公司水工研究所的無反射造波機試驗水槽中進行。水槽的長、寬、高分別為68.0 m、1.0 m、1.6 m。造波機系統由造波板、伺服電機、造波機控制器、計算機控制系統和數據采集、分析系統組成。該造波機系統于2005年6月從日本三井造船株式會社引進，是國內成功引進的第一座無反射造波機成套設備。該系統可在0.5耀4.5 s的周期范圍內模擬不同譜型的不規則波和特定形式的非線性波，并可以在水槽中生成海嘯。本次研究為了保證試驗準確性，試驗水槽應滿足以下三點要求：1）水槽地形鋪設平整，2）造波系統可精確控制，3）測量儀器及數據采集系統的精度高。

1.1坐標系統定義

試驗水槽里鋪設坡度為β的水泥面斜坡，坐標定義示意圖見圖1，試驗中保證海嘯波最大爬高不越過地形最高處，相對位置的坐標原點0定義于靜水面與斜坡交界的岸線點，x*、y*軸代表常用的二維笛卡爾坐標系統，離岸向及向上各為x*軸、y*軸的正方向。β為均勻斜坡的坡度角，d為斜坡前平底地形段的水深值。海嘯波在等水深的平底段起始波高為H，沿斜坡爬升的最大爬坡高度為R。試驗中測定入射波高H的位置，考慮為了避免受到斜坡的反射影響需要在波浪最前端到達斜坡之前測量。故定義介于波峰與前方波面為5%H位置間的有限長度為L。

圖1　海嘯波沿緩坡爬高試驗坐標及相關物理量定義Fig.1　The coordinates and definitions of related physical variables for tsunami wave run-up on the mild slope

1.2試驗水槽地形鋪設

無反射造波水槽一端安有造波機，尾端鋪設大塊石進行消波，以保證每組試驗后水槽中水面快速恢復平穩。本次試驗在水槽中部分別鋪設了1/15.3、1/30.12兩組均勻坡度的水泥面。圖2為斷面水槽的斜坡布置側視圖，圖中標示了水槽尺寸和地形鋪設位置。由圖中可以看出不同坡度的斜坡配置中1/15.3的斜坡起點離造波板位置為22.16 m，斜坡高度為1.0 m；1/30.12的斜坡起點離造波板位置為22.66 m，斜坡高度為0.5 m，斜坡后方設有長度為2.62 m的平段。

1.3試驗布置

為測量海嘯波在斜坡上的爬高變形過程及最大爬坡高度，本次試驗在1/15.3、1/30.12的斜坡試驗中沿水槽方向布設了29支波高計，其中6支波高計安裝在靜水位與斜坡交界線以上，22支波高計安放在靜水位以下的斜坡上方，1支波高計安放在斜坡前方的平段處，用來測量入射波高。考慮到海嘯波在斜坡上傳播至淺水區域時波浪形態變化劇烈，因此原點前1 m及后2 m范圍內波高計間隔為25 cm，斜坡上10 m范圍內波高計間隔為50 cm，這些儀器可同步測量海嘯波在斜坡上傳播過程中的試驗數據。

圖2　試驗水槽布置側視圖Fig.2　Side view of flume arrangement

同時為了有效觀測海嘯波在斜坡上爬到的最大高度，試驗在水槽坡面上布置了長為20 m的皮尺。由于不同的水位下靜水位與斜坡的交界位置不同，因此需要根據試驗工況調整所有儀器安放的位置。

圖3為以1頤15.3坡度為例，給出了靜水位為58.7 cm工況時的試驗儀器布置俯視圖。

圖3　試驗儀器布置俯視圖Fig.3　Top view of experimental instruments

1.4海嘯波模擬

試驗以孤立波近似模擬海嘯，孤立波的模擬采用Goring（1978）的造波板運動計算方法。Goring造波方法是基于永形波假定，考慮在水槽一端的造波機推波板作水平方向運動，假設推波板處的水質點運動水平速度與推波板運動速度相等，理論上孤立波的波長為無限長，因此波高為0的位置發生于相位在依肄，實際上受限于推波板的位移精度及運動的時間。本次試驗水槽造波機具有模擬孤立波的功能，理論波形與造波機實際造出的試驗波形對比見圖4。

由圖中可以看出除了輕微的尾波外，造波機推出的孤立波波形與理論一致。尾波的產生是由于Goring（1978）的方法所模擬的波形在尾波不對稱導致的，整體看，本次試驗水槽可以正確模擬孤立波。

圖4　試驗波形及理論波形對比圖Fig.4　Comparison chart of experimental and theoretical waveforms

1.5試驗工況

試驗在1頤15.3斜坡下分次進行3組平底水深條件為29.4 cm、44.0 cm以及58.7 cm的爬高試驗。而后重新鋪設1頤30.12的均勻斜坡，進行了平底水深為29.4 cm的孤立波爬高試驗。通過以上4種工況下的孤立波爬高試驗，進一步分析水槽試驗中海嘯波在不同坡度斜坡上的傳播及爬高特性，試驗工況組合見圖5，共計101組試驗。

Fig.5　Theexperimental combination of different slopewith the wave height and wave depth ratio

圖6　海嘯波沿1頤15.3斜坡爬高照片及無量綱化爬高（d=58.7 cm，初始時刻H/d=0.155，cotβ=15.3）Fig.6　Snapshot of wave breaking during run-up on a slope of 1:15.3,and dimensionless spatial wave surface elevation （d=58.7 cm and H/d=0.155 and cotβ=15.3）

2　結果討論

2.1海嘯波沿斜坡爬高特性分析

通過在水槽中布置密集的波高計同步測量海嘯波沿斜坡傳播的特性，圖6為孤立波在d= 58.7 cm，H/d=0.155的試驗工況下沿1頤15.3斜坡爬坡時波浪傳播破碎的狀態及水槽中有代表性的部分波高計測量的波面過程。

由圖中可以看出當海嘯波經過靜水位附近時，由于水深逐漸變淺波峰的形狀越來越陡，波峰表面處出現白色水花，破碎后水花會以較快的速度繼續向坡面上方爬升，直至水體的動能全部轉化成勢能為止，而后又因為重力作用快速退回到靜水位附近，并產生震蕩。圖中波面過程及波高計的位置均以造波機前水深d進行無量綱化，時間以轉換成了無量綱時間，時間的原點定義為海嘯波波峰通過斜坡坡腳的瞬間。由無量綱化的波面過程圖可以看出海嘯波從平底段沿斜坡傳播，在x*為0的位置即靜水位與斜坡的交界處，波峰前端幾乎呈直立狀，與海嘯傳播至岸邊時描述的“水墻”相似。另外由圖中不同位置處的波面過程對比可以看出，孤立波在斜坡上移動速度逐漸減慢。由這兩張圖可以看出，孤立波自造波機處傳播，在等水深處波高變化不大，當進入斜坡段時（x/d<15.3），波峰面逐漸抬高，波速變小，波前端形狀變陡直至破碎，破碎后水體前端逐漸接近不連續階梯狀。這與部分學者得到的結論一致[5-8]。

2.2海嘯波沿斜坡最大爬高經驗公式

海嘯波最大爬高高程根據前人的文獻[2]可得出其經驗公式分為非破碎以及破碎兩種情況，試驗中依據Pedersen&Gjevik（1983年）提出的破碎波判定關系H/d<0.479（cosβ）-10/9進行判斷，考慮到cosβ在15～60區間內，非破碎工況下H/d范圍在0.005～0.02，在模型試驗中很難觀測[9]，并且需要較長的傳播距離，因此本次海嘯波沿斜坡最大爬高擬合的公式適用的范圍是破碎的海嘯波。

破碎的海嘯波最大爬高高度，Synolakis[2]由坡度為1頤19.85的試驗數據，歸納出其爬高公式為：

Li&Raichlen（2003）[10]利用數值模擬方法，處理了海嘯波的破碎過程，考慮孤立波的能量變化，建立了能量守恒方程，由計算歸納出估算最大爬高高度的經驗公式為：式中：EI為海嘯波的起始總能量；EB為破碎波消耗的能量，破碎波消耗的能量與起始總能量的比的公式如下，其中A1、B1、C1均為H/d的經驗系數。EB/EI=C1（A1ln（cotβ）+B1）（3）

另外Hsiao等人[3]由他在大比尺水槽里得到的1頤60斜坡試驗數據以及前人的試驗數據歸納出了最大爬高高度的經驗公式為：

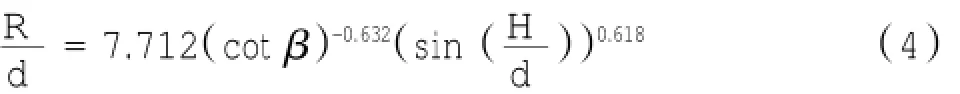
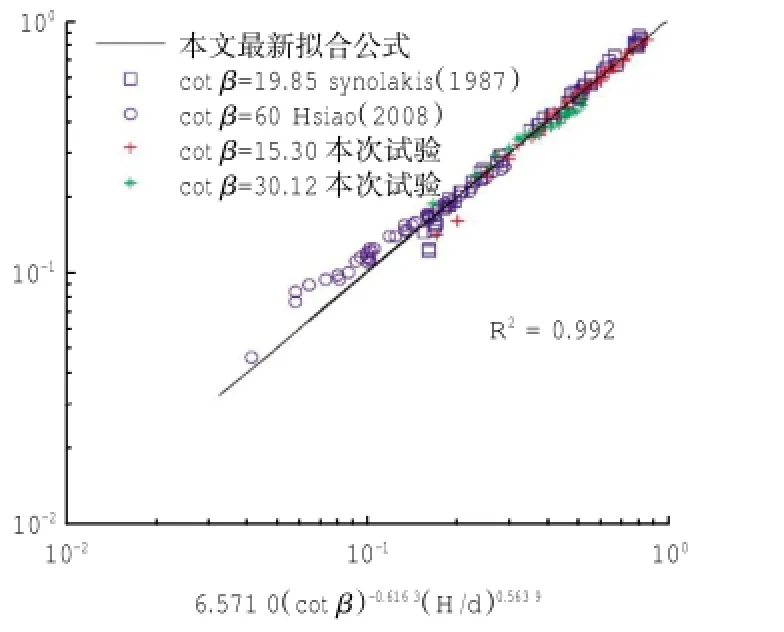
公式（1）僅為1頤19.85這一種單一斜坡坡度試驗數據擬合結果，對其他坡度不適用。公式（2）是從能量角度出發，但是能量耗散只涉及到波浪破碎，而未考慮底部摩擦和表面張力等的影響，因此也有局限性。公式（4）是Hsiao等人[3]根據1頤15、1頤19.85、1頤30及1頤60四種不同坡度的試驗數據擬合出的經驗公式，但是其中部分試驗數據年代較早，且H/d包含的范圍小于0.45。因此本文在前人工作的基礎上，通過擬合本次試驗1頤15.3以及1頤30.12兩種坡度4種工況的爬高試驗數據，并結合Synolakis[2]的1頤19.85的破碎海嘯波試驗數據、Hsiao等人[3]的1頤60的破碎海嘯波試驗數據，利用最小二乘法擬合出一個新的破碎海嘯波爬高公式，其中0.01

圖7　無量綱最大爬坡高度實測值與本文擬合公式相關性Fig.7　Correlation between the measured data and fittingformula of dimensionless maximum run-up

圖8分別給出了無量綱化的海嘯波最大爬高數據分別與公式（1）、公式（2）、公式（4）、公式（5）的對比情況。由圖中可以看出公式（2）、公式（4）、公式（5）在H/d小于0.3時，其估算結果比較相近，當H/d逐漸變大時，公式（2）估算結果與實測值成相反的趨勢，公式（4）及公式（5）估算結果較為相近，并且由于加入了本次試驗的最新數據，公式（5）在H/d>0.4時優于公式（4）。

3　結語

本次研究通過在無反射造波水槽中產生孤立波模擬海嘯的傳播，建立了1頤15.3以及1頤30.12兩種不同坡度的模型，旨在通過大量的試驗數據擬合出更適用于估算H/d在較大范圍內變化的海嘯波沿緩坡爬升的最大爬高公式，并且通過試驗觀察海嘯波近岸淺水變形的特性。

1）海嘯波在較深的等水深處傳播時波高變化不大，當進入斜坡段時，波峰面逐漸抬高，波速變小，在靜水位與斜坡交界的位置處，波峰前端幾乎呈直立狀，與海嘯傳播至岸邊時描述的“水墻”相似，破碎后水體前端逐漸接近不連續階梯狀，而后繼續向斜坡上方爬升。整個作用過程中，破壞性最強的階段是靜水位接近破碎時，且破碎后水體會有個加速過程，向岸方向爬升，即為海嘯波淹沒陸地的過程。

圖8　無量綱最大爬坡高度實測值與經驗公式對比Fig.8　Comparison between the measured data and empirical formula of dimensionless maximum run-up

2）通過最小二乘法擬合本次試驗1頤15.3、1頤30.12兩種坡度4種工況的爬高試驗數據以及Synolakis[2]1頤19.85、Hsiao等人[3]1頤60的試驗數據，提出了一個新的破碎海嘯波爬高公式6，其判定系數R2=0.992。

3）由于公式擬合需要大量的實測數據作為依據，因此下一階段需要進行更多的水槽試驗，對已經提出的公式進行修正，提高其適用范圍。

參考文獻：

[1]HALL J V J,WATTS G M.Laboratory investigation of the vertical rise of solitary waves on impermeable slopes[Z].USACE,1953.

[2]SYNOLAKIS C E.The run-up of long waves[D].Pasadena：Cali原fornia Institute of Technology,1986.

[3]HSIAO S C,HSU T W,LIN T C,et al.On the evolution and run-up of breaking solitary waves on a mild sloping beach[J].Coast Eng., 2008,55：975-988.

[4]SYNOLAKIS C E.The runup of solitary waves[J].Journal of Fluid Mechanics,1987,185：523-545.

[5]張金牛，吳衛，劉樺，等.孤立波作用下斜坡堤越浪量的實驗研究[J].水動力學研究與進展A輯，2014，29：656-662. ZHANG Jin-niu,WU Wei,LIU Hua,et al.An experiment study on overtopping of solitary wave against a slope dike[J].Chinese Jour原nal of Hydrodynamics,2014,29:656-662.

[6] 趙曦.海嘯波生成、傳播與爬高的數值模擬[D].上海：上海交通大學，2011. ZHAO Xi.Numerical simulation of generation,propagation and runup of tsunamis[D].Shanghai:Shanghai Jiao Tong University, 2011.

[7] 宣瑞韜.海嘯波爬高的水槽實驗研究[D].上海：上海交通大學，2013. XUAN Rui-tao.An experimental study on run-up of tsunami waves in wave flume[D].Shanghai:Shanghai Jiao Tong University, 2013.

[8]蔣昌波，楊武，陳杰，等.孤立波作用下沿海路基沖刷實驗研究[J].海洋工程，2014，32（5）：34-39. JIANG Chang-bo,YANG Wu,CHEN Jie,et al.Experimental study on scour around the coastal road by solitary waves[J].The Ocean Engineering,2014,32(5):34-39.

[9]EUGENY Buldakov.Tsunami generation by paddle motion and its interaction with a beach:Lagrangian modelling and experiment[J]. Coastal Engineering,2013,80:83-94.

[10]LI Y,RAICHLEN F.Energy balance model for breaking solitary wave run-up[J].Journal of Waterway Port Coastal&Ocean Engi原neering,2003,129:47-59.

E-mail：wenzhong78@vip.sina.com.cn

中圖分類號：U652.3

文獻標志碼：A

文章編號：2095-7874（2016）01-0042-06

doi：10.7640/zggwjs201601010

收稿日期：2015-07-14修回日期：2015-09-17

作者簡介：張文忠（1969— ），男，河北樂亭縣人，碩士，高級工程師，主要從事港口及航道工程研究。

Experiment study of tsunami run-up on the mild slope

ZHANG Wen-zhong1,LYU Ying-xue1,LIU Xin2,HUANG Xuan-jun1
（1.CCCC Tianjin Port Engineering Institute Co.,Ltd.,Key Laboratory of Coastal Engineering Hydrodynamic,CCCC,Tianjin
300222,China;2.China Nuclear Power Design Co.,Ltd.,Shenzhen,Guangdong 518031,China）

Abstract：In order to better evaluate the range of tsunami waves propagating to the near shore,we analyzed the characteristics and the states of the deformation of the tsunami,through producing solitary wave in the absorbing wave maker tank to test the spread of the tsunami wave along the mild slope.The experimental data at slope 1頤15.3 and 1頤30.12 are obtained.Compared the empirical formula with other relevant studies,we proposed a new formula of the maximum tsunami run-up along the mild slope.The results show the good correlation between the empirical formula and rich measured data.

Key words：tsunami;mild slope;run-up;empirical formula;physical model test