基于主成分分析法的風電功率短期組合預測

吳金浩　楊秀媛　孫　駿

（北京信息科技大學，北京 100192）

基于主成分分析法的風電功率短期組合預測

吳金浩楊秀媛孫駿

（北京信息科技大學，北京 100192）

間歇性與不確定性是風力發電的固有特性，在風力發電迅速發展的背景下風電功率預測的重要性日漸凸顯。為了減少單一模型在個別預測點誤差較大的情況，提高整體預測方法的預測精度及相對誤差率，本文采用反向傳播（BP）神經網絡以及支持向量機（SVM）兩種基本模型進行組合，并引入粒子群（PSO）以及交叉驗證（CV）算法來優化模型中的參數。結合主成分分析法（PCA）對原始數據進行預處理，在不降低預測精度的前提下，對原數據進行降維處理從而提高運算效率。使用模型分別對未來5天進行預測，結果表明組合預測模型的標準平均誤差（NMAE）、標準均方根誤差（NRMSE）都滿足國內現行指標，而且預測精度比單一模型有很大提高，相對誤差更加穩定，有效減少了較大誤差點的出現。實例研究表明，基于主成分分析法的風電功率短期組合預測模型的可行性。

風功率預測；主成分分析法；BP神經網絡；粒子群算法；支持向量機；組合預測

隨著對風力發電的深入研究，風電固有的間歇性以及不確定性成為了制約其發展的主要因素。大容量風電場接入電網后，造成電網電壓、頻率的波動，給調度運行帶來很大困難，甚至威脅到電力系統的穩定運行。因此，及時、精確地預測風電功率是首先需要解決的問題［1-2］。

目前，已經有研究人員做了風電功率預測多種方面的研究。文獻［3］使用時間序列法建模，得到預測時刻與前段時刻風速的關系，并確定神經網絡輸入變量數目，這種方法本質是基于時間序列模型，在風況發生突變時無法準確預測，對較長時間的預測也無法得到精確結果；文獻［4］理論分析得出風功率由風速、風向等因素決定，使用數值天氣預報系統收集的歷史數據，建立BP神經網絡模型，在風電場實裝顯示預測效果良好，模型預測誤差在15%左右，需要進一步優化或者開發更精確的預測模型；文獻［5］將粒子群（PSO）算法與基于前向神經網絡模型相結合，從而提高功率預測的精度，結果顯示模型平均誤差以及標準差都有不同程度地下降，預測準確率高于優化前的結果；文獻［6］使用交叉熵理論來確定組合預測的權值，先分析各預測模型的交叉程度，再根據公式求取權值，結果顯示使用交叉熵理論的組合模型精度較高。

目前傳統的組合預測的只是解決了單一預測模型可能出現較大誤差的問題，但基礎組合算法本身精度并不高，而且普遍存在運算時間較長、無法在工程上應用的問題。本文先對基礎算法進行優化，提高BP神經網絡與SVM的精度再進行組合，這樣整體預測效果獲得很大提升。然后使用主成分分析法對原始數據進行主成分分析數據預處理，在不降低預測精度的前提下減少運算時間。實測數據研究表明，本文提出的組合預測模型可以穩定、高效的完成預測任務，具有很大工程應用的潛力。

1　主成分分析法

主成分分析法（principal components analysis，PCA）是一種多元統計分析方法，利用降維的思想在少量信息損失的前提下，將多個指標轉化為若干綜合指標［8］。因此，面對多輸入因素的問題，只需考慮幾個主要的組成部分，從而使問題得到簡化，提高分析效率。結合本文風電功率預測模型，可用于解決預測模型輸入變量多、部分變量之間相關、運算時間過長的問題。

理論分析表明：主成分是原數據矩陣的協方差矩陣的特征向量的線性組合，它們是互不相關的，其方差為數據矩陣的特征根。計算出矩陣的特征根值并按照順序排列為λ1≥λ2≥…≥λp＞ 0。其中，第一主成分的貢獻率定義為，是第一主成分的方差與總方差和的比值；前兩個主成分的貢獻率定義為，前k個主成分的累計貢獻率定義為。當前k個主成分的貢獻率達到85%，就可以認為主成分可以代替原始數據。

選擇風速、風向、溫度、濕度和壓強五個因素作為預測模型的輸入項。對風向分別進行正弦、余弦計算，得到六維的原始輸入數據，然后運用PCA對原數據分析處理。

2　預測模型及優化方案

2.1預測模型的選擇

風電輸出功率與風速、風向等多種因素有關，使用傳統的建模方式很難精確表達。人工智能方法如BP神經網絡、SVM等具有較強的非線性學習能力，能通過統計數據學習得到其內在關系。BP神經網絡與SVM都具有很強的模式分類和非線性函數逼近能力，BP神經網絡采用的是基于經驗風險最小化原則，而SVM是基于結構風險最小化原則，考慮的是經驗風險和置信界之和的最小化。兩種方法在非線性函數擬合方面各有優勢，具有組合互補的可行性。

2.2BP神經網絡模型與粒子群算法參數優化

BP（Back Propagation）神經網絡是一種按誤差逆向傳播算法訓練的多層前饋網絡（Multilayer Feedforward Neural Networks，MFNN）模型［11］。網絡結構如圖1所示，u和y分別是網絡的輸入、輸出向量，網絡由輸入層、隱層和輸出層節點組成，前層至后層節點通過權值連接。

圖1　BP神經網絡示意圖

傳統的BP神經網絡使用梯度下降法調整參數，這種方法相鄰兩次迭代的搜索方向是正交的，迭代在向極小值靠近的過程中，走的是曲折的路徑，使得網絡收斂速度下降，可能找到的是局部極值而不是整體極值。為解決這些問題，采用粒子群優化算法（Particle Swarm Optimization，PSO）來進行參數尋優。粒子群算法是一種群體智能算法，根據生物種群特性，所有粒子都將跟隨最優粒子在空間中移動，直到找到問題的極值。PSO算法優化BP神經網絡整體流程如圖2所示。

圖2　PSO-BP神經網絡流程圖

2.3支持向量機模型與交叉驗證算法參數優化

支持向量機（support vector machine，SVM）是90年代中期發展起來的基于統計學理論的一種機器學習方法，通過尋求結構風險最小來提高學習機泛化能力，在統計樣本數量較少時也能獲得良好的統計規律［12］。SVM主要任務是在空間中尋找一個最優超平面來逼近目標函數，其基本原理如圖3所示。

圖3 SVM原理示意圖

圖3中，H為分類超平面；1H和2H為距分類超平面最近的兩平行面；mL為兩平面間隔。假設樣本是線性可分的，任務就是實現把樣本點分開，且保證分類間隔盡可能大。實際情況多數樣本都是線性不可分的，使用一個非線性映射，把低維的輸入數據映射到高維特征空間，然后在高維空間內尋找最優分類平面。

當使用SVM模型進行回歸預測時，尋找最優的懲罰參數c和核函數參數g能得到比較理想的預測準確率。本文使用交叉驗證法（cross validation，CV）來確定參數c和g，首先將原始數據分成K組，將每個子集數據分別做一次驗證集，其余的K-1組子集數據作為訓練集，這樣會得到K個模型，用這K個模型最終的驗證集的分類準確率的平均數作為交叉驗證法下分類器的性能指標。CV算法優化SVM整體流程如圖4所示。

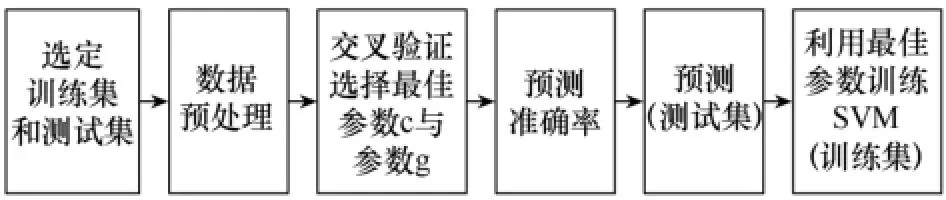
圖4　CV-SVM流程示意圖

3　風電功率預測的組合模型

3.1組合模型的概念

組合預測就是使用多種預測方法對同一模型預測，根據不同的計算規則確定預測方法的權值，最后整合為一個綜合模型［17］。采用組合預測法消除單一預測方法中的較大誤差，提高整體模型的穩定性。

假設使用m種方法對模型分別預測，單一預測方法的預測值分別為fi， i=1，2，…，m 。則組合預測可表示為f=l1f1+l2f2+…+lmfm，其中l1， l2，…，lm為各種預測方法的加權系數。組合預測的主要任務是確定各預測方法的權值，下文給出三種常見的加權系數計算方法。圖5經過優化的BP神經網絡與SVM預測模型的組合示意圖。

圖5　組合預測模型

3.2算術平均法

算術平均法也稱為等權平均法，對m種單項預測模型取相同的權值，即各模型比重相同。算術平均法適用于無法確定單項預測模型詳細精確度的情況。由于算術平均方法計算簡單，工程上可以快速得出結果，適用性比較強。

系數計算式：

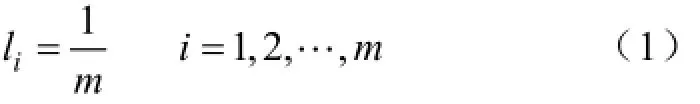
3.3預測誤差平方和倒數法

預測誤差平方和倒數法，考慮到每種方法的預測精度，是一種非等權值的計算方法。需要先計算出每種預測的誤差平方和，這個值越大對應的預測精度就越低，相應模型的權值也會比較小，再根據系數計算公式求取每種模型的權值，該方法更符合客觀規律。

系數計算公式：

式中，itx為第i種方法在第t時刻的預測值，tx為同一對象在第t時刻的觀測值，ite為第i種單項預測方法在第t時刻的預測誤差。

3.4二項式系數法

二項式系數法也是一種非等權計算方法，具體做法與平方和倒數不同。需要先求各單一預測模型的誤差方差和Eii，再對其進行排序，不妨設E11＞E22＞…＞Emm。根據統計學中位數的概念，排在中間模型對應的權系數最大，遠離中位數的模型權系數較小。

系數計算式：

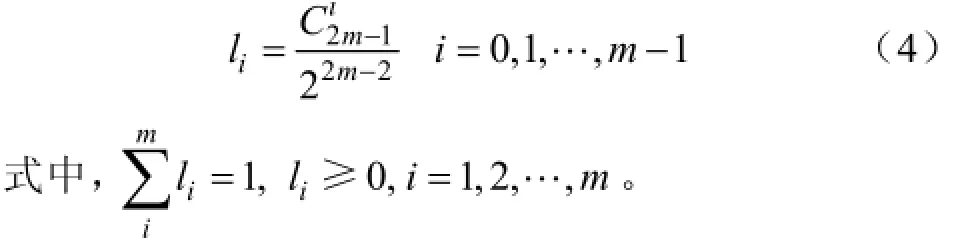
4　風電功率預測評估指標

國家能源局2011年發布的《風電場功率預報管理暫行辦法》規定風電場功率預測系統提供的日預測曲線最大誤差不超過25%；實時預測誤差不超過15%；全天預測結果的均方根誤差應小于20%［19］。

現行行業標準［20］及文獻廣泛采用標準平均誤差（normalized mean absolute error， NMAE）、標準平均相對誤差（normalized mean relative error，NMRE）、標準均方根誤差（normalized root mean square error， NRMSE）等來評估風功率預測效果。NMAE指預測值與真實值之間平均相差多少，是絕對誤差的平均值；NMRE是指絕對誤差占真實值的百分比；NRMSE是觀測值與真實值偏差的平方和觀測次數n比重的平方根，反映預測的精密度。

式中，x（i） 為樣本真實值；x′（i）為樣本預測值；capP是風電場的額定裝機容量；N為預測樣本個數。本文采用前兩個指標來評估預測模型。

5　算例分析

5.1風電場基本情況

本文算例風電場裝備80臺額定容量1.5MW的雙饋感應風力發電機組（WPG-DFIG），總裝機容量為120MW，風機輪轂高度65m，葉輪直徑58m。連續采集2013年5月的各項數據，數據分辨率為15min。使用5月前26天數據訓練模型，首先選擇5月27日作為預測日，預測長度為一天，即96個點。每一點輸入項為風機實時風速、風向、溫度、濕度和壓強五個因素，輸出項為風電機組實時輸出功率。然后使用訓練好的模型，分別對28、29、30、31日進行預測并作誤差分析。

5.2PCA數據預處理

首先對數據進行歸一化處理，統一各參數的量綱。風速歸一化采用公式對實時風速進行處理，式中vmax為歷史最大風速。氣溫、氣壓、濕度的歸一化方法與風速一致。風向可能在0°～360°之間變化，只對風向取正弦值或余弦值并不能完全區分0°～360°內所有風向，因此風向要取正弦、余弦兩個值來描述。歸一化后訓練數據為一個2496×6的矩陣，預測數據為一個96×6的矩陣。

然后進行主成分提取，計算歸一化后訓練數據的協方差矩陣，求出協方差矩陣的特征根及貢獻率并依據累積貢獻率提取主成分，計算結果見表1。

由表1可知前三個特征值累計貢獻率已達96.9719%，說明前三個主成分基本包含了全部信息，取前三個特征值，計算出相應的特征向量，計算結果見表2。

表1　特征值及貢獻率

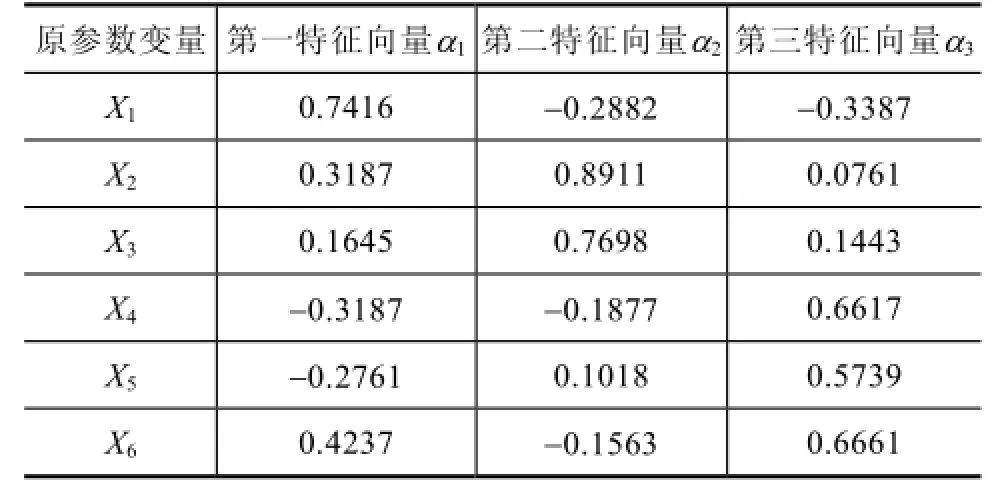
表2　特征向量表

通過特征向量寫出主成分表達式如下：

第一主成分：

第二主成分：

第三主成分：

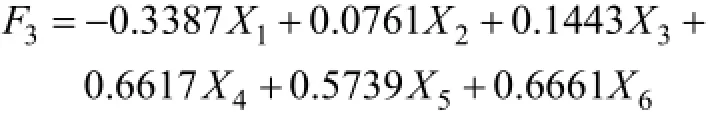
通過上述表達式對數據進行PCA處理，則訓練數據轉換為2496×3的矩陣，預測數據轉換為96× 3的矩陣。處理后變為3個輸入參數，這3個輸入互不相關且包含原來參數所有的信息。原來幾項參數之間互有聯系，全部作為輸入會導致信息冗余，經過PCA處理后可以在不影響精度的情況下，提高運算速度。

5.3單一模型的預測

對于BP神經網絡模型，選用包含一個隱含層的3層網絡，隱層神經元傳遞函數采用S型正切函數，輸出層神經元傳遞函數采用S型對數函數。進過PCA數據預處理后，輸入變為3維，隱層節點數定為7。方向傳播使用梯度下降法調整權值和閾值。然后使用粒子群算法優化BP神經網絡的初始權值和閾值，進化次數定為30，種群規模定為60。為防止粒子盲目搜索，將其位置和速度分別限制在區間［5，5］-［0，1］。

表3是兩種預測方法的標準平均誤差、標準均方根誤差以及訓練時間。圖6是兩種預測方法得到的一天時間（96個點）預測結果。可以看出，BP神經網絡可以基本完成預測任務，經過粒子群算法參數尋優后預測精度得到進一步提高，但某些點明顯存在誤差過大的情況，單獨使用這一種模型效果不佳。

表3　神經網絡模型預測誤差及訓練時間

圖6　神經網絡模型預測效果對比

對于支持向量機模型，使用徑向基函數作為核函數，svmtrain程序中的懲罰參數c和核函數g，任意給定兩個較小的值。然后使用交叉驗證的方法，通過計算可以找到一定意義最佳的參數c和g。

表4是兩種預測方法的標準平均誤差、標準均方根誤差以及訓練時間。圖7是兩種預測方法得到的一天時間（96個點）預測結果。可以看出，經過交叉驗證參數尋優后預測精度有所提高，但兩種預測模型也存在在某些點誤差比較明顯的情況。SVM預測精度與BP神經網絡的預測精度在同一水平，而且誤差較大的點并不一致，這是下文兩種模型組合的基礎。

表4　支持向量機模型預測誤差及訓練時間

圖7　支持向量機模型預測效果對比

5.4組合模型的預測

兩種經過參數優化后的模型PSO-BP以及CV-SVM的標準平均誤差均小于15%，標準均方根誤差均小于20%，且數值在同一數量級，符合組合預測的要求。根據上文計算公式得到三種模型的權系數見表5，三種組合模型預測誤差及訓練時間見表6，組合模型的預測結果如圖8所示，相對誤差如圖9所示。

由于圖8可以直觀看到，組合預測的預測效果十分明顯。其中平方和倒數模型的預測精度最高，其標準平均誤差為9.31%，標準均方根誤差為12.63%，比單一預測模型以及其他方法相比優勢明顯。由于選取的兩種模型本身精度差距不大，因此可以看到算術平均模型的精度排第二，在工程上使用可以犧牲精度而提高效率。二項式模型效果較差，這是由于本文只選取了兩種模型組合，如選三種及以上數量的模型組合，二項式模型就能發揮很好的作用。三種模型的預測時間基本等同于原來兩種預測模型的時間之和。由圖9可以看出基本上預測點誤差值能保持在一點范圍內，顯示出了組合預測模型平穩的優勢。圖中只有一個點有相對誤差大于10%，但不能排除該數據本身有誤的可能性。

表5　三種組合模型權系數

表6　三種組合模型預測誤差及訓練時間

圖8　三種組合模型的預測結果

圖9　三種組合模型的預測相對誤差

使用平方和倒數組合模型分別對5月28日、29日、30日、31日進行預測，并作誤差分析，結果如表7所示，而且無較大相對誤差的出現。最后可以得出使用本文的組合模型能有效減少較大誤差的出現，提高預測精度的結論。

表7　未來4日預測誤差及訓練時間

6　結論

本文基于實測數據，先使用PCA方法對數據進行降維處理，后建立組合預測模型預測未來24h風力發電功率。從數據預測效果和誤差分析，可以得到以下結論：

1）主成分分析法可以對觀測變量降維，能夠客觀地反映影響風功率預測的各種影響因素，在保證預測精度的前提下提高運算速度。

2）經過參數優化后PSO-BP神經網絡與CV-SVM模型可以獲得高的預測精度，兩種模型精確度在同一水平而且誤差較大的點不盡相同，適合進行模型組合。

3）分別求出算術平均法、誤差平方和倒數法、以及二項式系數法的權值，分析得出組合預測可以有效減少較大誤差的出現，從而提高預測精度。本文兩種模型組合的情況，誤差平方和倒數法模型精度最高。

4）組合預測受基礎預測模型精度的限制，因此選擇合適的兩種或者多種組合模型是關鍵。目前風電功率物理預測模型發展迅速，未來可以考慮將歷史數據外推模型與物理模型組合起來，以應對各種復雜地形、不同天氣條件下預測任務。

［1］ 何東， 劉瑞葉. 基于主成分分析的神經網絡動態集成風功率超短期預測［J］. 電力系統保護與控制，2013， 4（4）： 50-54.

［2］ 周松林， 茆美琴， 蘇建徽. 基于主成分分析與人工神經網絡的風電功率預測［J］. 電網技術， 2011， 35（9）：128-132.

［3］ 楊秀媛， 肖洋， 陳樹勇. 風電場風速和發電功率預測研究［J］. 中國電機工程學報， 2005， 25（11）： 1-5.

［4］ 范高鋒， 王偉勝， 劉純. 基于人工神經網絡的風電功率短期預測系統［J］. 電網技術， 2008（22）： 72-76.

［5］ 楊志凌， 劉永前. 應用粒子群優化算法的短期風電功率預測［J］. 電網技術， 2011， 05（5）： 159-164.

［6］ 陳寧， 沙倩， 湯奕， 等. 基于交叉熵理論的風電功率組合預測方法［J］. 中國電機工程學報， 2012（4）：29-34， 22.

［7］ 孟安波， 陳育成. 基于虛擬預測與小波包變換的風電功率組合預測［J］. 電力系統保護與控制， 2014，3（3）： 71-76.

［8］ 羅毅， 劉峰， 劉向杰. 基于主成分—遺傳神經網絡的短期風電功率預測［J］. 電力系統保護與控制，2012（23）： 47-53.

［9］ 王麗婕， 冬雷， 高爽. 基于多位置NWP與主成分分析的風電功率短期預測［J］. 電工技術學報， 2015， 5（5）： 79-84.

［10］ 王麗婕， 冬雷， 廖曉鐘， 等. 基于小波分析的風電場短期發電功率預測［J］. 中國電機工程學報， 2009（28）：30-33.

［11］ 范高鋒， 王偉勝， 劉純， 等. 基于人工神經網絡的風電功率預測［J］. 中國電機工程學報， 2008（34）：118-123.

［12］ 王賀， 胡志堅， 仉夢林. 基于模糊信息粒化和最小二乘支持向量機的風電功率波動范圍組合預測模型［J］. 電工技術學報， 2014（12）： 218-224.

［13］ Ernst B， Oakleaf B， Ahlstrom ML， et al. Predicting the wind［J］. Power and Energy Magazine， IEEE， 2007，5（6）： 78-89.

［14］ Peiyuan C， Pedersen T， Bak-Jensen B， et al. ARIMA-based time series model of stochastic wind power Generation［J］. IEEE Transactions on Power Systems， 2010， 25（2）： 667-676.

［15］ Chen Xia， Dong Zhaoyang， Meng Ke， et al. Electricity price forecasting with extreme learning machine and bootstrapping［J］. IEEE Transactions on Power Systems，2012， 27（4）： 2055-2062.

［16］ 劉純， 范高鋒， 王偉勝， 等. 風電場輸出功率的組合預測模型［J］. 電網技術， 2009（13）： 74-79.

［17］ Rodrigues AB， Da Silva MD. Confidence intervals estimation for reliability data of power distribution equipments using bootstrap［J］. IEEE Transactions on Power Systems， 2013， 28（3）： 3283-3291.

［18］ Khosravi A， Nahavandi S， Creighton D. Prediction intervals for Short-Term wind farm power Generation forecasts［J］. IEEE Transactions on Sustainable Energy，2013， 4（3）： 602-610.

［19］ 風電場功率預測預報管理暫行辦法［S］. 北京： 國家能源局， 2011

［20］ 風電功率預測功能規范［S］. 北京： 國家電網公司，2011.

The Combination Forecasting Model for Wind Farm Power based on PCA

Wu Jinhao Yang Xiuyuan Sun Jun（Beijing Information Science and Technology University， Beijing 100192）

Intermittency and uncertainty is the inherent characteristics of the wind power and in the rapid development of wind power generation background the importance of wind power forecasting is becoming more and more obvious. In order to reduce the error of the single model and are improve the prediction accuracy and relative error rate of the whole forecasting method， the paper combine two basic models of BP neural network and support vector machine（SVM）， and introduce the particle swarm and cross validation to optimize the parameters. The original data are preprocessed by principal component analysis （PCA）. In the premise of little reducing the accuracy of prediction， the original data is reduced to the dimension of the original data to improve the operation efficiency. The results show that the NMAE and NRMSE of the combined forecasting model meet the domestic current index. And the accuracy of the model is improved， and the relative error is more stable. This method can effectively reduce the appearance of large errors. In the final， these prove the feasibility of the combination forecasting model for wind farm power based on PCA.

wind power forecast； principal components analysis （PCA）； BP neural network； particle swarm； support vector machine （SVM）； forecast combination

國家自然科學基金（51377011）

吳金浩（1988-），男，山東省濟寧市兗州區人，本科，主要從事風電場與水電廠協同運行研究工作。