調速型鼠籠式異步磁力聯軸器的軸向力研究

楊超君, 章友京, 張　濤, 陳志鵬, 孔令營

(1. 江蘇大學 機械工程學院, 江蘇 鎮江 212013; 2. 江蘇大學 電氣信息工程學院, 江蘇 鎮江 212013)

?

調速型鼠籠式異步磁力聯軸器的軸向力研究

楊超君1, 章友京1, 張濤2, 陳志鵬1, 孔令營1

(1. 江蘇大學 機械工程學院, 江蘇 鎮江 212013; 2. 江蘇大學 電氣信息工程學院, 江蘇 鎮江 212013)

調速型鼠籠式異步磁力聯軸器即永磁調速器,它的力學參數、磁場分布對其傳遞能力及整個系統的穩定性與可靠性具有很大的影響,因此有必要對其工作時的軸向力進行深入研究.基于等效面電流法,推導出聯軸器在低轉差率下的螺旋進給/退出軸向力計算表達式;同時采用電磁場分析軟件Magnet對其進行模擬分析,得到了不同嚙合長度、不同轉差率下的螺旋進給/退出軸向力值,并進行了對比分析.調速型鼠籠式異步磁力聯軸器軸向力由完全嚙合狀態至脫離狀態呈現先增大后減小的趨勢;在相同輸入轉速情況下,轉差率越大,軸向力越小,在脫離狀態時趨于穩定值.這對于調速型鼠籠式異步磁力聯軸器以及其它類型磁力聯軸器的理論研究、參數設計與優化及其應用都有著一定的理論意義及實際應用價值.

永磁調速器; 等效面電流法; 軸向力; 電磁分析

調速型鼠籠式異步磁力聯軸器即永磁調速器[1],是在普通永磁磁力聯軸器的基礎上發展而來的一種新型的調速傳動裝置.永磁調速器作為一種新興的節能調速設備,在國外已經被成功應用于工業與軍事上[2-4],在國內也被應用于石化、電力等行業.與變頻調速設備相比,永磁調速器采用純機械式結構,消除了電力諧波及電磁干擾,實現了軟啟動及過載保護,有助于提高系統的穩定性和可靠性[5-6].

調速型異步磁力聯軸器作為一種新型傳動調速裝置,具有結構簡單、過載保護、節能效果顯著等優點[1，5].如圖1所示,調速型鼠籠式異步磁力聯軸器機械結構主要由永磁轉子和導體轉子組成.磁力聯軸器在非完全嚙合時,由于模型并不對稱，會有一定的軸向力產生,并且由于嚙合長度的變化，軸向力會隨之變化.軸向力的大小直接關系到磁力聯軸器工作時的穩定性,尤其是在進行連續調速的情況下,用來調節嚙合長度的執行機構承受交變載荷會影響磁力聯軸器調速的精確性.因此,軸向力的研究對于調速型磁力聯軸器的理論研究、參數設計與優化及其應用都有著一定的理論及實際意義.

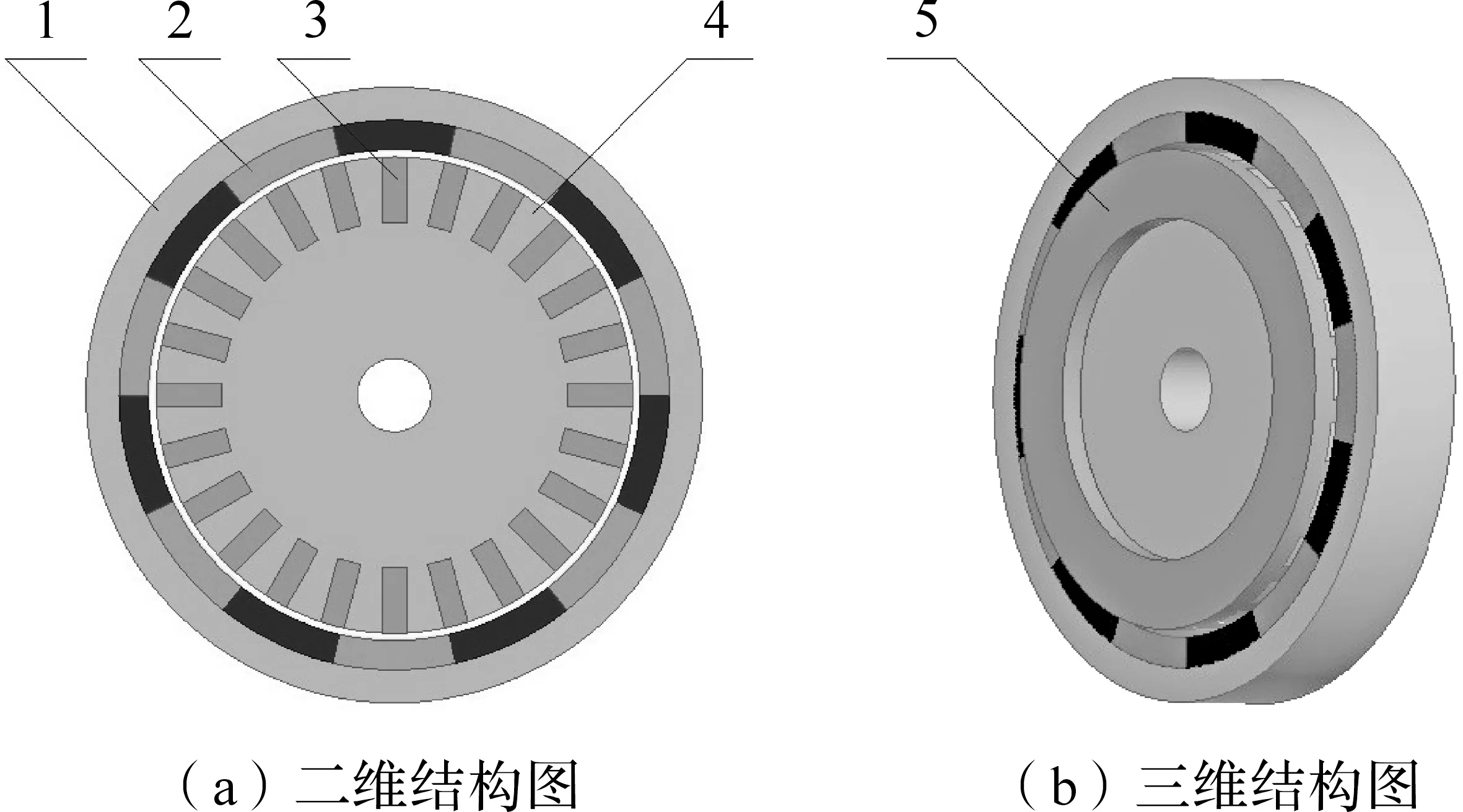
1—外轉子軛鐵; 2—永磁體; 3—銅導條; 4—內轉子軛鐵; 5—銅導體端環.圖1　調速型鼠籠式異步磁力聯軸器Fig.1　Adjustable speed squirrel-cage asynchronous magnetic coupling

1　聯軸器的原理和結構

調速型鼠籠式異步磁力聯軸器的結構如圖1所示,主要由永磁體2、銅導體3、外軛鐵1及內軛鐵4組成.各永磁體均為徑向充磁，但相鄰永磁體間充磁方向相反,其工作原理是銅導體切割永磁體磁場產生感應電流,感應電流產生的感應磁場與原永磁磁場相互耦合來傳遞動力[7].通過調節內外轉子的軸向位置可改變永磁體2與導體3之間的嚙合長度,從而控制其傳遞動力的能力,從而實現負載轉速、轉矩的調節.

2　軸向力的假設及計算

本文軸向力是指調速型鼠籠式異步磁力聯軸器內外轉子上受到的沿軸方向的力,內外轉子受到的軸向力大小相等、方向相反.調速型鼠籠式異步磁力聯軸器通過調節內外轉子軸向的嚙合長度改變轉速,為了系統可以精確并穩定地運行,內外轉子的軸向位置必須控制精確,因而軸向力的存在對磁力聯軸器的工作性能有較大影響.為了磁力聯軸器精確穩定地運行,需對軸向力進行研究分析.

2.1軸向力的分析和假設

計算永磁體磁場的方法有解析法、有限元法、等效磁網絡法和數值解析結合法[8].目前,對磁場及磁力計算主要采用有限元等數值計算法以及有限幾種典型結構的經驗公式法[9].有限元等數值計算法雖然具有較高的計算精度,但計算較為繁雜而且不能顯式表達磁場或磁力與各參數之間的相互關系.故本文通過引入等效面電流法,解析出動態空間磁場分布,進而求解出軸向力的計算表達式.

如圖1所示,磁力聯軸器由內、外兩個轉子組成,其中內轉子為銅導體,外轉子為永磁體.聯軸器工作時,外轉子轉動形成旋轉磁場,內轉子導體切割磁力線形成感應電流,感應電流產生感應磁場,與外轉子永磁體的旋轉磁場耦合產生轉矩,通過調節永磁體與導體之間的嚙合長度就可以控制傳遞的轉矩,從而實現負載轉速的調節.

基于等效面電流法作出如下假設:

1)永磁體徑向均勻磁化,氣隙是均勻的;

2)軛鐵將磁力線封閉,有較高的磁導率且未磁化飽和,忽略邊緣效應及漏磁;

3)永磁體的退磁曲線為一直線,回復線與退磁曲線重合,即永磁體磁導率為定值；

4)導磁材料被永磁體徑向均勻磁化,不存在體電流,只存在面電流；

5)理論計算中只考慮聯軸器工作在靜態下的情況,故忽略銅導體切割磁力線產生的感應磁場對氣隙磁場的影響.

2.2軸向力的理論計算

根據畢奧-沙伐定理,建立異步磁力聯軸器的直角坐標系,見圖2,坐標原點在磁力聯軸器端面的中點處.利用永磁體等效面電流法,可得永磁體在空間磁場中任意場點的磁感應強度表達式為[10]

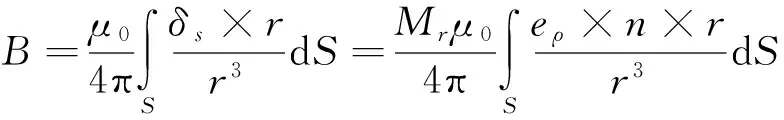
(1)

式中：B為空間磁密;δs為等效面電流;μ0為真空磁導率;r為源點到場點的矢量路徑;Mr為徑向磁化強度;eρ是徑向磁化強度在永磁體邊界面上的單位向量;n是永磁體邊界面的外法線單位向量.

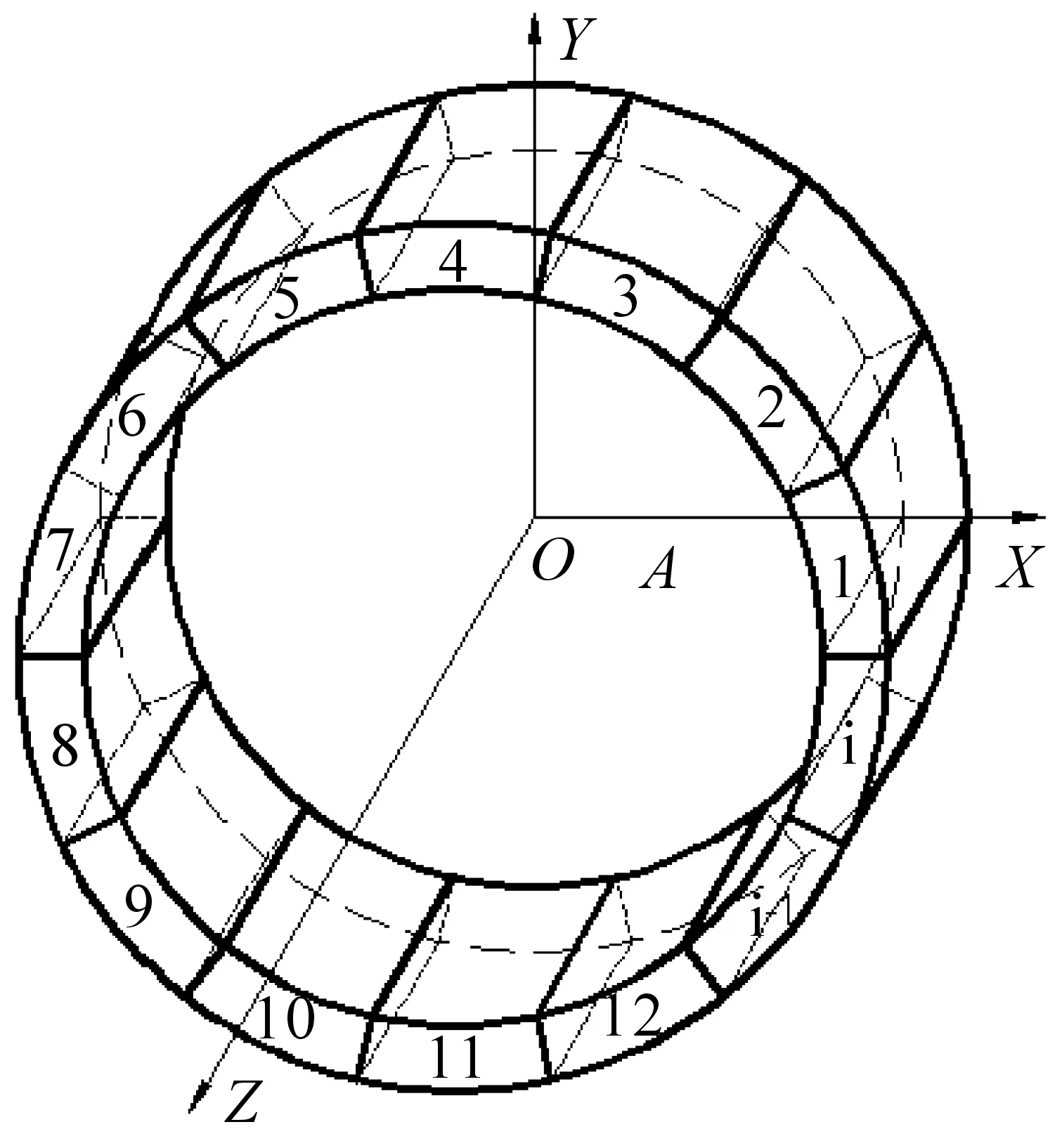
圖2　永磁轉子模型Fig.2　Model of permanent magnet rotor

為了便于分析計算,應用等效面電流法將單極永磁體模型等效為永磁體4個表面BCDE，FGHI，BCFG，EDHI的等效面電流,分別求出各等效面電流在氣隙中任一點A產生的磁感應強度B,見圖3.

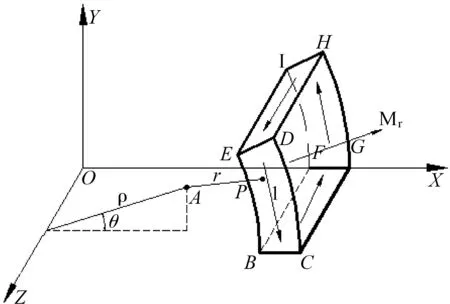
圖3　單塊永磁體的數學模型Fig.3　Mathematical model of single block permanent magnet

1)永磁體BCDE面上等效面電流在A點產生的磁感應強度B1為[11]

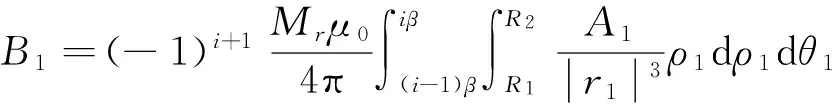
(2)

其中：

A1=(Z1-Z-vt)cos(θ1+ωt)x+(Z1-Z-vt)

sin(θ1+ωt)y+[ρcos(θ-θ1-ωt)-ρ1]z；

R1為永磁體內部半徑;R2為永磁體外部半徑;β為單塊永磁體的磁極張角；ω為永磁轉子的角速度;v為永磁轉子的軸向進給速度;i為永磁體編號，i=1,2,…,np，np為磁極對數.

2)永磁體FGHI面上等效面電流在A點產生的磁感應強度B2為

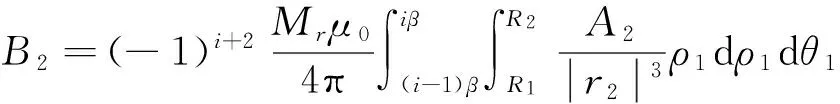
(3)

其中：

A2=(Z1-Z-vt)cos(θ1+ωt)x+(Z1-Z-vt)

sin(θ1+ωt)y+[ρcos(θ-θ1-ωt)-ρ1]z.

3)永磁體BCFG面上等效面電流在A點產生的磁感應強度B3為

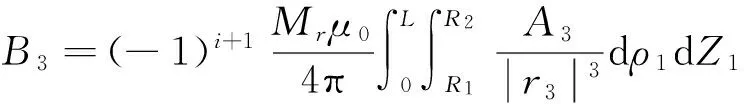
(4)

其中：

A3=[ρsinθ-ρ1sin((i-1)β+ωt)]x-

[ρcosθ-ρ1cos((i-1)β+ωt)]y.

4)永磁體EDHI面上等效面電流在A點產生的磁感應強度B4為

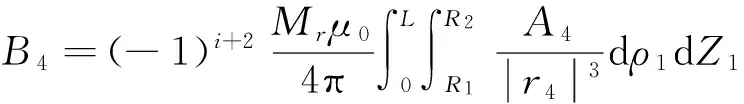
(5)

其中：

A4=[ρsinθ-ρ1sin(iβ+ωt)]x-

[ρcosθ-ρ1cos(iβ+ωt)]y.

故可以得到所有永磁體在A點產生的磁感應強度，為

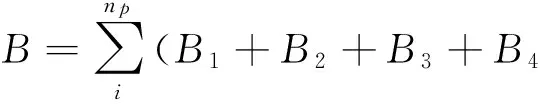
(6)

假設磁場在導磁材料區域的分布均勻,故可得到簡化的電磁力[11-12]為

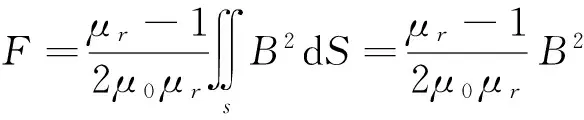
(7)

根據式(6)計算得到的磁感應強度,由式(7)及式(1)可以得出單塊永磁體對于點A處的電磁力為[13]

(8)

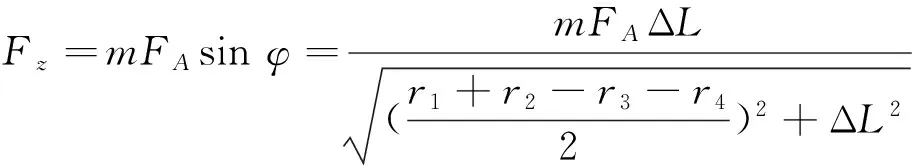
(9)

式中：ΔL為軸向位移長度;r1為外轉子外部半徑;r2是外轉子內徑;r3是內轉子外徑;r4是內轉子內徑;φ為夾角;m是永磁體的極數.

3　軸向力的模擬分析

由于調速型磁力聯軸器在工作時做雙自由度運動,既繞水平軸旋轉,又沿水平軸軸向移動(見圖4),故選用Magnet電磁場仿真軟件,分析調速型鼠籠式異步磁力聯軸器從完全嚙合狀態至脫離狀態的軸向力.聯軸器模型的主要結構參數如下:永磁轉子磁極對數為7,內轉子槽數為24,槽深為18mm,槽寬為6.5mm,永磁體軸向長度為26mm,端環軸向長度為6mm.

圖4　調速器運動示意圖Fig.4　Motion diagram of the machine

如圖5所示為主動轉子轉速為1 500r/min、軸向退出速度為0.08m/s時,不同轉差率下的螺旋退出軸向力隨時間的變化曲線.從圖5可知,4條曲線都以零點為起點.這是由于在完全嚙合狀態,聯軸器處于平衡位置,各個方向的合力為0.螺旋進給的軸向力隨著時間的增加先增大后減小,在260—280ms即軸向偏移為20.8～22.4mm時達到最大值,在400ms時刻即脫離狀態時達到最小值.軸向力在到達峰值前,4條曲線較為稀疏,轉差率對其影響較大;但在到達峰值后,4條曲線變得較為緊密,轉差率對其影響逐漸下降；在400ms時刻,各轉差率的軸向力相差無幾.

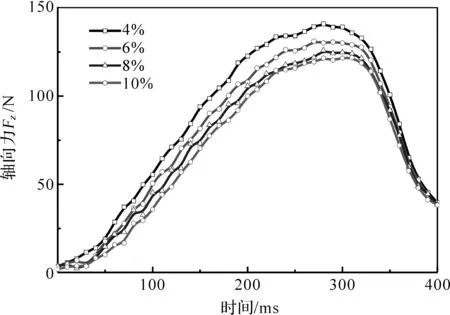
圖5　螺旋退出軸向力時變圖Fig.5　Time varying axial force diagram in the process of the screw out

圖6為4%，6%，8%，10%轉差率下軸向力的最大值.1 500r/min時最大值分別為141,136.77,125.6,124.5N;1 000r/min時最大值分別為151.3,141,139.97,131.9N；800r/min時的最大值分別為149.17，144.3，139.25，138.97N.隨著輸入轉速的增加,軸向力逐漸降低.

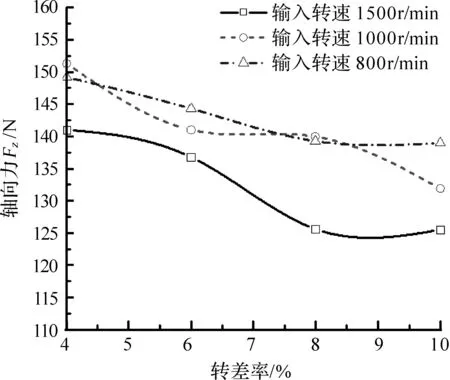
圖6　不同轉速下的最大軸向力Fig.6　Maximum axial force with different input speed

圖7為調速型鼠籠式異步磁力聯軸器輸入轉速為1 500r/min、軸向退出速度為0.08m/s時,不同轉差率下的螺旋退出至固定軸向偏移長度0，4，8，12，16，20，24，28，32mm的連續軸向力時變圖.如圖7所示,隨著時間的變化,軸向力先增大后減小,曲線呈現階梯狀爬升而后下降的趨勢.其中,軸向力最大值位于固定軸向偏移長度20～24mm區間,分別為128.6，131.17，138.15，147.1N;軸向力最小值位于固定軸向偏移長度32mm處,分別為25.8，25.9，26.1，26.2N.由圖中曲線可以看出：軸向力在到達峰值前,處于負加速度爬升狀態,相鄰固定軸向偏移長度的軸向力之差不斷減小;當運動至固定偏移長度并僅做旋轉運動時,軸向力波動類似于正弦波作周期性振動;在越過峰值后,軸向力急速下降至最小值.同時,從圖中可以看出,在同一軸向偏移長度的情況下,軸向力隨著轉差率的變大而變小.這是由于隨著調速器主從轉子間的轉差率的變大,導體轉子切割磁力線引起的感應電流所產生的反磁勢會隨之變大,從而削弱了氣隙磁場強度,使得軸向力變小.當軸向偏移長度為32mm時,此時調速器處于脫離狀態,導體轉子幾乎不能切割磁力線產生感應電流形成反磁勢,故轉差率對其影響降至最低.

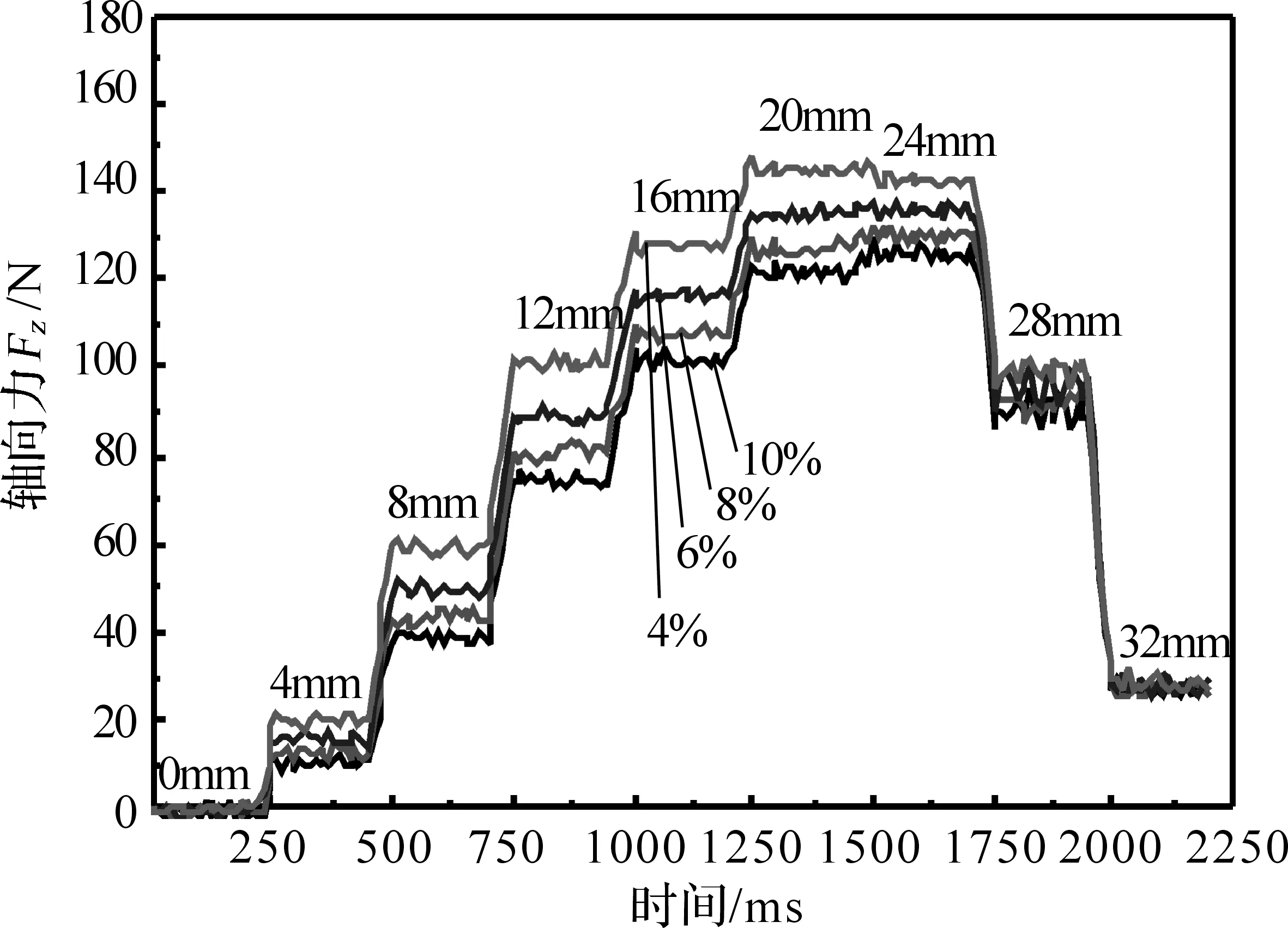
圖7　螺旋退出過程中的軸向力Fig.7　The axial force in the process of the screw out

圖8　固定軸向偏移的軸向力均值Fig.8　Mean axial force for fixed axial deviation

圖8為主動轉子轉速為1 500r/min、不同轉差率下的軸向力均值隨不同軸向偏移長度的變化曲線圖.從圖中可知,軸向力均值曲線呈現先增大后減小的趨勢.隨著轉差率的增大,軸向力也隨之變小.在軸向偏移長度32mm即脫離狀態時,各轉差率下的軸向力均值趨于穩定值26N.由公式(9)可知,嚙合長度ΔL=0時,軸向力Fz=0,隨著ΔL的增加,Fz逐步增大,但同時BA隨嚙合長度的增加逐步減小,導致FA逐步減小,當FA減小到一定程度,會抵消ΔL增大對FA的影響,此時出現軸向力最大值,隨著FA進一步減小,軸向力Fz逐步減小至0,趨勢與模擬一致.

4　結　論

從等效面電流理論出發,推導出調速型鼠籠式異步磁力聯軸器在低轉差率下的動態空間磁場分布及螺旋進給/退出軸向力計算表達式,然后進行模擬分析,得到結論如下:

1)調速型鼠籠式異步磁力聯軸器由完全嚙合狀態至脫離狀態過程中,軸向力呈現先增大后減小的趨勢,最大值出現在脫離過程中;

2)調速型鼠籠式異步磁力聯軸器在相同輸入轉速情況下,轉差率越大,軸向力越小,在脫離狀態時趨于穩定值;

3)調速型鼠籠式異步磁力聯軸器由完全嚙合狀態至脫離狀態過程中,轉差率對軸向力的影響逐漸變小,在同一軸向偏移長度的情況下,軸向力隨著轉差率的變大而變小.

[1]WALLACEA,vonJOUANNEA,JEFFRYESR,etal.Comparisontestingofanadjustable-speedpermanent-magneteddy-currentcoupling[C].IEEEPulpandPaperIndustryTechnicalConference.Atlanta:IEEEServiceCenter,2000:73-78．

[2]WALLACEA,vonJOUANNEA.Industrialspeedcontrol:arePMcouplingsanalternativetoVDFs[J].IEEEIndustryApplicationsMagazine,2001,7(5):57-63.

[3]HIGHFILLGS,HALVERSONLA.Loweringtotalcostofownershipwithbreakthroughmagnetictorquetransfertechnology[C].2006IEEECementIndustryTechnicalConferenceRecord.Atlanta:IEEEServiceCenter,2006:15．

[4]POTGIETERJohannesHJ,KAMPERMJ.Optimumdesignandcomparisonofslippermanent-magnetcouplingswithwindenergyascasestudyapplication[J].IEEETransactionsonIndustryApplications,2014,50(5):3223-3234．

[5]LUBINT,REZZOUGA.Steady-stateandtransientperformanceofaxial-fieldeddy-currentcoupling[J].IEEETransactionsonIndustrialElectronics,2015,62(4):2287-2296．

[6] 王旭,王大志,劉震,等.永磁調速器的渦流場分析與性能計算[J].儀器儀表學報,2012,33(1):155-160．

WANGXu,WANGDa-zhi,LIUZhen,etal.Eddycurrentfieldanalysisandperformancecalculationsforadjustablepermanentmagneticcoupler[J].ChineseJournalofScientificInstrument,2012,33(1):155-160．

[7]MOHAMMADIS,MIRSALIMM,VAEZ-ZADEHS,etal.Analyticalmodelingandanalysisofaxial-fluxinteriorpermanent-magnetcouplers[J].IEEETransactionsonIndustrialElectronics,2014,11(61):5940-5947．

[8] 章躍進,江建中,屠關鎮.應用數值解析結合法計算旋轉電機磁場[J].電工技術學報,2004,19(1):7-11．

ZHANGYue-jin,JIANGJian-zhong,TUGuan-zhen.Researchonnumericalandanalyticalcombinedmethodofmagnetfieldcomputationforrotationalelectricalmachines[J].JournalofElectrotechnics,2004,19(1):7-11．

[9] 田錄林,賈嶸,楊國清,等.永磁鐵磁貼合體的磁場及磁力[J].電工技術學報,2008,23(6):7-13．

TIANLu-lin,JIARong,YANGGuo-qing,etal.Themagneticfieldandmagneticforceofpermanentmagnetaffixedtoaplanemagnetizer[J].JournalofElectrotechnics,2008,23(6):7-13．

[10] 管春松.盤式異步磁力聯軸器的電磁特性與溫度場性能研究[D].鎮江:江蘇大學機械工程學院,2012：31-33．

GUANChun-song.Studyonelectromagneticpropertiesandthermalfieldinaxialasynchronouspermanentmagnetcouplings[D].Zhenjiang:JiangsuUniversity,SchoolofMechnicalEngineening,2012:31-33．

[11] 王晶晶.雙層實心異步磁力聯軸器渦流及溫度場分析[D].鎮江:江蘇大學機械工程學院,2009：24-25．

WANGJing-jing.Doublesolidinductionmagneticcouplingeddycurrentandtemperaturefieldanalysis[D].Zhenjiang:JiangsuUniversity,SchoolofMechanicalEngineering，2009：24-25．

[12] 張宏.新型節能調速設備永磁磁力耦合調速器的原理及應用[J].中國電力教育,2009,2(14):552-553．

ZHANGHong.Newenergy-savingequipmentprincipleandapplicationofpermanentmagneticcoupling[J].ChinaPowerEducation,2009,2(14):552-553．

[13] 王瑜.永磁裝置中磁場力的計算[J].磁性材料及器件,2007,38(5):49-52．

WANGYu.Calculationofmagnetforceofpermanentmagnetdevices[J].MagneticMaterialsandDevices,2007,38(5):49-52．

Analysis of axial force of adjustable speed squirrel-cageasynchronous magnetic coupling

YANG Chao-jun1, ZHANG You-jing1, ZHANG Tao2, CHEN Zhi-peng1, KONG Ling-ying1

(1. School of Mechanical Engineering, Jiangsu University, Zhenjiang 212013, China;2. School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China)

Mechanical parameters and the magnetic field distribution of the adjustable speed squirrel-cage asynchronous magnetic coupling are closely related to the ability to transmit electromagnetic torque and the stability and reliability of the entire system. Therefore, it is necessary to study the axial force on working condition deeply. Based on equivalent surface current method, the calculation expression of rotary feeder/exit axial force was obtained through using three-dimensional analysis. By using Magnet (one kind of electromagnetic field analysis software), the value of rotary feeder/exit axial force was solved under the different length of engagement and different slip ratio, and then the comparative analysis was done. The axial force of adjustable speed radial squirrel-cage asynchronous magnetic coupling showed a trend of decrease after the first increase from complete meshing state to out of state. The greater slip, the smaller axial force, and it got stable value when the adjustable speed squirrel-cage asynchronous magnetic coupling was out of state under the condition of the same input speed. The study on the axial force has a certain theoretical significance and practical value in the field of theory, parametric design optimization and application in the research of adjustable speed squirrel-cage asynchronous magnetic coupling and other types of asynchronous magnetic coupling in the future.

permanent magnetic coupling; equivalent surface current method; axial force; electromagnetic analysis

2015-03-10.

江蘇省自然科學基金資助項目(BK20131254).

楊超君(1965—)，女，江蘇無錫人，博士，教授，博士生導師，從事智能磁力機械、機械產品虛擬仿真技術、機械CAD/CAE和激光加工技術等研究，E-mail：yangchaojun@ujs.edu.cn.通信聯系人：章友京(1991-)，男，安徽績溪人，碩士生，從事智能磁力機械與控制研究，E-mail:735688913@qq.com.http://orcid.org//0000-0002-2423-1095

10.3785/j.issn. 1006-754X.2016.03.014

TH 133.4

A

1006-754X(2016)03-0282-05

本刊網址·在線期刊：http://www.journals.zju.edu.cn/gcsjxb