元模型層次的UML動態(tài)子圖到Coq形式規(guī)范的轉(zhuǎn)換

竇　亮　尹　敏　李　超　楊宗源

(華東師范大學計算機科學技術(shù)系　上海 201100)

?

元模型層次的UML動態(tài)子圖到Coq形式規(guī)范的轉(zhuǎn)換

竇亮尹敏*李超楊宗源

(華東師范大學計算機科學技術(shù)系上海 201100)

UML動態(tài)子圖主要包括序列圖和狀態(tài)圖等，它們在描述系統(tǒng)的行為方面應(yīng)用廣泛，但是半形式化的語義使它們不能直接進行形式化驗證。Coq是目前主流的交互式定理證明器，用形式化的Coq規(guī)范來描述UML動態(tài)子圖模型，可以在此基礎(chǔ)上進行對模型的屬性進行驗證等工作。基于現(xiàn)有工作，提出將UML動態(tài)子圖模型轉(zhuǎn)換為Coq形式規(guī)范的框架，在元模型層次給出狀態(tài)圖和序列圖的轉(zhuǎn)換規(guī)則，介紹算法和原型工具實現(xiàn)。這種元模型層次的轉(zhuǎn)換方法，保證了轉(zhuǎn)換前后的語法正確性，為進一步分析驗證提供了基礎(chǔ)。

UML動態(tài)子圖模型轉(zhuǎn)換元模型Coq Kermeta

0　引　言

UML[1]是面向?qū)ο蠼M織(OMG)提出的建模語言，能在各種抽象層次對系統(tǒng)進行描述和建模，被廣泛應(yīng)用在系統(tǒng)的設(shè)計階段。如果在設(shè)計階段就對UML模型進行驗證，能盡早地發(fā)現(xiàn)系統(tǒng)錯誤，提高軟件質(zhì)量，減少開銷。然而，目前的UML規(guī)范缺乏精確的形式語義定義，因此難以進行進一步的分析驗證。為了給UML進行精確的語義定義，許多研究工作采用了形式化方法。形式化方法是用于系統(tǒng)規(guī)范定義、開發(fā)和驗證等方面的基于數(shù)學的方法，利用適當?shù)臄?shù)學分析方法，以提高系統(tǒng)的可靠性與安全性。用形式語言來描述UML模型可以彌補UML自身的缺陷，消除開發(fā)人員對系統(tǒng)設(shè)計理解的不一致性。

Coq[2]是基于歸納構(gòu)造演算的高階定理證明器，在跨計算機科學和數(shù)學領(lǐng)域的研究中，Coq已經(jīng)成為一個強有力的工具，它可以作為形式化驗證程序的開發(fā)環(huán)境，也已經(jīng)成為研究人員對復雜語言的定義進行描述和推理的標準工具。基于定理證明器Coq對各種基礎(chǔ)軟件的語義進行形式化描述和驗證是當前的一個研究熱點[3-5]。在之前的工作[6，7]中，我們提出將UML序列圖轉(zhuǎn)換為Coq形式規(guī)范描述，在Coq定理證明器中證明了語義的相關(guān)屬性，但是從UML序列圖到Coq形式規(guī)范的轉(zhuǎn)換過程是手動完成的，這種方式的轉(zhuǎn)換效率較低，且不能保證轉(zhuǎn)換的正確性。

本文提出了一種元模型層面的轉(zhuǎn)換框架，設(shè)計了元模型層面的轉(zhuǎn)換規(guī)則，提出了針對狀態(tài)圖和序列圖這兩種UML動態(tài)子圖到Coq形式規(guī)范的轉(zhuǎn)換算法，并在Kermeta[8]中實現(xiàn)了自動轉(zhuǎn)換的原型工具。這種轉(zhuǎn)換不針對某一具體的動態(tài)子圖模型，而是在元模型層面上完成UML元模型到Coq形式規(guī)范的映射，使得轉(zhuǎn)換結(jié)果符合目標抽象語法，保持了UML動態(tài)子圖模型完整的語義成分。

本文的基本內(nèi)容如下：首先介紹元模型和Kermeta，并給出本文研究的UML狀態(tài)圖和序列圖的元模型定義；接著依次介紹UML狀態(tài)圖和序列圖轉(zhuǎn)換為Coq形式規(guī)范的具體實現(xiàn)，包括轉(zhuǎn)換框架、轉(zhuǎn)換規(guī)則和算法幾個方面；然后通過實例展示了轉(zhuǎn)換后生成的Coq形式規(guī)范；最后介紹相關(guān)工作并總結(jié)。

1　背景介紹

1.1元模型和Kermeta

OMG組織提出的元對象機制(MOF)是一個四層的元建模框架，在這個體系結(jié)構(gòu)中依次有元元模型層、元模型層、模型層和對象層。每一層都可以看成是上一層的實例，繼承了上層模型的元語義；同時又是下一層的抽象，為下一層模型建立了創(chuàng)建模型的元語言。MOF是自描述的，所以不再需要元元元模型。MOF用于定義面向?qū)ο笤Ｐ停湫偷木褪荱ML建模語言，在元模型層面進行模型轉(zhuǎn)換能保證轉(zhuǎn)換前后的模型符合元模型[9]。

Kermeta是一種可執(zhí)行的元建模語言，可描述模型的結(jié)構(gòu)和行為，支持元模型層面的轉(zhuǎn)換。Kermeta工具集成在Eclipse中，與OMG的EMOF標準兼容。Kermeta語言具有多種特性，包括命令式編程、面向?qū)ο缶幊獭⒚嫦蚰Ｐ途幊獭⒚嫦蚍矫婢幊毯推跫s式開發(fā)等特性。

1.2狀態(tài)圖和序列圖的元模型定義

在Kermeta中實現(xiàn)模型轉(zhuǎn)換，需要指定源/目標元模型，以一個符合源元模型的源模型作為輸入。因此，要進行模型轉(zhuǎn)換就需要指定源元模型，下面介紹本文研究的UML狀態(tài)圖和序列圖的元模型，分別如圖1和圖2所示。本文給出的UML狀態(tài)圖和序列圖元模型在UML2.0給出的標準元模型上略有刪減，并且使用Kermeta自帶的Ecore進行構(gòu)建和繪制。

圖1　狀態(tài)圖的元模型

圖1是狀態(tài)圖的Ecore元模型。StateModel是該元模型最頂層的類。本文轉(zhuǎn)換后生成的狀態(tài)圖抽象語法定義，支持衛(wèi)式條件的使用，考慮了狀態(tài)的進入/退出動作、歷史狀態(tài)記錄機制，支持層間轉(zhuǎn)移描述，是較為完整全面的狀態(tài)圖語法定義。

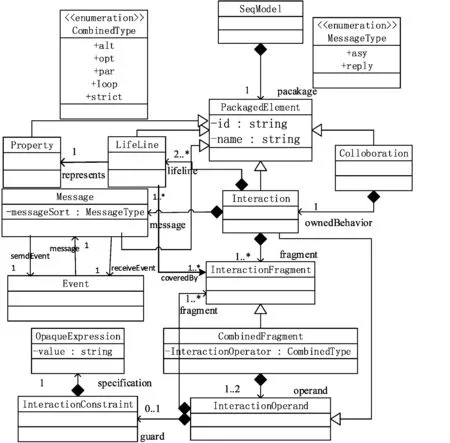
圖2　序列圖的元模型

圖2是序列圖的Ecore元模型。SeqModel是元模型最頂層的類。本文轉(zhuǎn)換后生成的序列圖抽象語法定義除了考慮消息、生命線、組合片段等元素，還考慮了交互操作符、衛(wèi)式條件等元素，涵蓋了序列圖的主要交互操作符片斷定義。

2　轉(zhuǎn)換工作

2.1轉(zhuǎn)換框架

模型轉(zhuǎn)換需要保證轉(zhuǎn)換前后模型語法和語義的正確性與完整性，UML圖中包含大量的語法和語義信息，直接在模型層面上進行轉(zhuǎn)換很可能會導致轉(zhuǎn)換前后模型信息的丟失。本文在Kermeta中實現(xiàn)的元模型層次的轉(zhuǎn)換工具框架如圖3所示，其中UML元模型和模型都屬于UML規(guī)范范疇，而Coq中對UML的抽象語法定義和UML刻畫的實際模型代碼符合Coq規(guī)范，轉(zhuǎn)換規(guī)則是用Kermeta進行編寫的。具體地，T1是將UML元模型定義為形式化的Coq抽象語法的過程，通過手工編碼實現(xiàn)；T2和T3是模型轉(zhuǎn)換的過程：首先，引入符合元模型的模型，然后，利用轉(zhuǎn)換規(guī)則將UML模型轉(zhuǎn)換為Coq形式規(guī)范代碼，并最終保存為Coq文件，以便在后續(xù)的定理證明工作中使用；T4利用了Kermeta的面向方面編程特性，直接將轉(zhuǎn)換規(guī)則織入UML元模型中；T5表明UML模型符合UML元模型，即模型是元模型的實例；T6表明轉(zhuǎn)換生成的Coq代碼符合Coq中對UML圖抽象語法的形式規(guī)范定義。

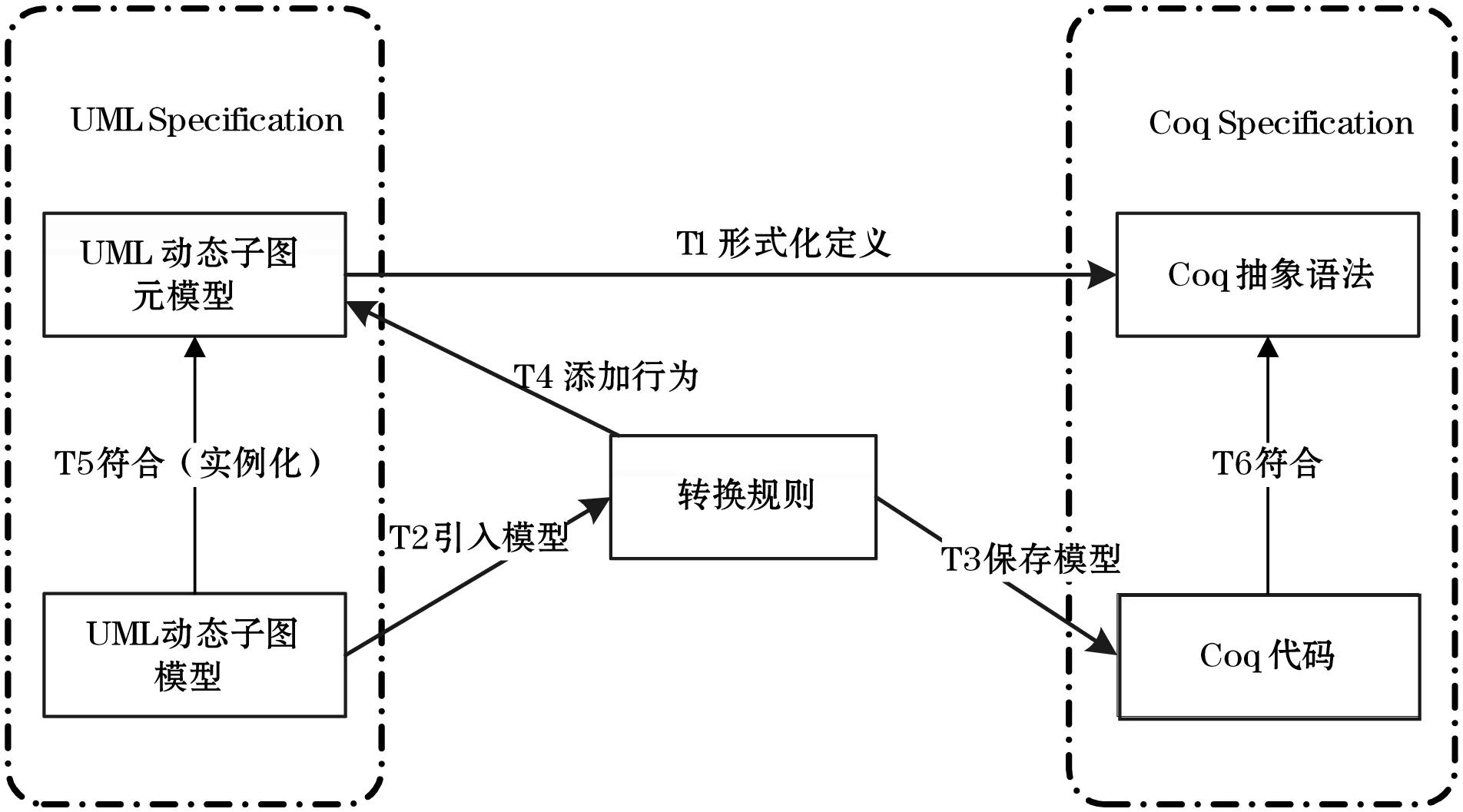
圖3　轉(zhuǎn)換框架

該轉(zhuǎn)換框架具有如下的優(yōu)點：

1. 層次清楚，分離關(guān)注，轉(zhuǎn)換規(guī)則如果需要變更，只需要修改轉(zhuǎn)換規(guī)則層即可；

2. 具備模型無關(guān)性，在元模型層面定義轉(zhuǎn)換規(guī)則，使得任意符合該元模型的模型都可以使用該轉(zhuǎn)換規(guī)則進行轉(zhuǎn)換，和特定模型定義的內(nèi)容沒有關(guān)系；

3. 采用了XMI來表示UML模型，使得可以使用不同的建模工具來對目標系統(tǒng)進行建模，方便模型的保存和引入。

2.2狀態(tài)圖的轉(zhuǎn)換規(guī)則和算法

從圖1中可看出狀態(tài)圖元模型的主要語法單元包括State、Transition、Behavior、Event等。為了將狀態(tài)圖模型轉(zhuǎn)換為Coq形式規(guī)范，首先在Coq中為這些元素定義抽象語法如下。這里使用歸納類型定義狀態(tài)圖，關(guān)于Coq的使用方法，可以參考文獻[10]。

Definition event:= string.

Definition sname:= string.

Definition tname:= string.

Definition action:= string.

Definition seqact:= list action.

Inductive history:Set:=

|none:history

|deep:history

|shallow:history.

Inductive bexp:Type:=

|BTrue:bexp

|BFalse:bexp

|BEq:aexp-> aexp-> bexp

|BLe:aexp-> aexp-> bexp

|BNot:bexp-> bexp

|BAnd:bexp-> bexp-> bexp

|BOr:bexp-> bexp-> bexp

|BImp:bexp-> bexp-> bexp.

(*衛(wèi)式條件的定義*)

Definition guard:= bexp.

Definition trans:= tname * nat * set sname * event * guard * seqact * set sname * nat * history.

Definition entryexit:= seqact * seqact.

(*狀態(tài)圖的抽象語法定義*)

Inductive sc:Type:=

|basic_sc:sname-> entryexit-> sc

|or_sc:sname-> list sc-> nat-> set trans-> entryexit-> sc

|and_sc:sname-> list sc-> entryexit-> sc.

接著定義元模型層面上的狀態(tài)圖到Coq形式規(guī)范的轉(zhuǎn)換規(guī)則：

(1) 狀態(tài)名、事件名和轉(zhuǎn)移名在Coq中都用字符串來表示，分別對應(yīng)sname、event和tname；

(2) 狀態(tài)的入口出口動作被映射成包含2個動作(action)列表的二元組；

(3) 狀態(tài)圖中的每個狀態(tài)都被映射為Coq抽象語法中定義的或狀態(tài)(or_sc)、基本狀態(tài)(basic_sc)和與狀態(tài)(and_sc)中的一種。例如：or_sc是包括狀態(tài)名、子狀態(tài)列表、活躍狀態(tài)序號、子轉(zhuǎn)移列表、入口出口動作的五元組；

(4) 每個衛(wèi)式條件(guard)都被映射為邏輯謂詞bexp規(guī)定類型中的一種；

(5) 每一個動作序列被映射為動作列表；

(6) 每個轉(zhuǎn)移都被映射為一個包含轉(zhuǎn)移名、源狀態(tài)序號、源狀態(tài)決定因子、觸發(fā)事件、衛(wèi)式條件、行為、目標狀態(tài)決定因子、目標狀態(tài)序號和歷史紀錄機制的九元組。為了處理轉(zhuǎn)移可能發(fā)生在不同層次的狀態(tài)之間的情況，用源目標決定因子和目標決定因子兩個元素進行指示。即，如果發(fā)生層間轉(zhuǎn)移，則源、目標狀態(tài)序號用來記錄最高層的源、目標狀態(tài)的序號，而決定因子用來記錄子層狀態(tài)的狀態(tài)名。

根據(jù)轉(zhuǎn)換規(guī)則，設(shè)計UML狀態(tài)圖到Coq形式規(guī)范的生成算法：首先，引入符合狀態(tài)圖元模型的狀態(tài)圖模型；其次，對模型進行分析，獲取模型中的狀態(tài)和轉(zhuǎn)移信息，并存儲在對應(yīng)的集合中；最后，按照轉(zhuǎn)換規(guī)則，將提取出來的狀態(tài)、轉(zhuǎn)移、衛(wèi)式條件等信息轉(zhuǎn)換為Coq形式規(guī)范代碼。算法描述如下：

算法1

TransList 狀態(tài)轉(zhuǎn)移信息的集合，初始為空

StateList 狀態(tài)集合，初始為空。包括簡單狀態(tài)、或狀態(tài)、與狀態(tài)，以及歷史紀錄狀態(tài)信息

//下述方法織入到元模型最頂層類StateModel上

operation toCoq():String

//通過下面2個方法獲取模型的信息，存儲在相應(yīng)集合

//最頂層的region調(diào)用getTransList方法

self.packagedElment.asType(StateMachine).region.one.getTransList();

//最頂層的Vertex調(diào)用getTransList方法

self.packagedElment.asType(StateMachine).region.one.subVertex.one.asType(Vertex).getStateList(TransList);

//將相應(yīng)集合中的狀態(tài)和衛(wèi)式條件進行編號

setStateID(StateList);

setGuardID(TransList);

re1 = Guard2Coq(TransiList.guard);

re2 = State2Coq();

re3 = Trans2Coq();

//返回轉(zhuǎn)換結(jié)果

return re1 + re2 + re3;

end

toCoq ()方法是整個算法的主線，該算法通過調(diào)用其他方法實現(xiàn)信息獲取、進行調(diào)整和轉(zhuǎn)換。對于模型信息的獲取，是通過getTransList()和getStateList()兩個方法實現(xiàn)的。getTransList()方法被織入到Region類上，而并沒有織入到Transition類上，主要是為避免重復獲取同一個trans的信息，所以從最頂層的region開始自頂向下地獲取所有trans的信息。getStateList()方法需要用到getTransList()獲得的信息，故放在getTransList()后執(zhí)行。這兩個方法的偽代碼如下：

aspect class Region{

operation getTransList()

//(1)處理最頂層的region中的每個transition元素

foreach trans in transition

//當目標狀態(tài)為歷史狀態(tài)時

if(self.target.isHistory(self.target)) then

trans.tState = trans.parent;

trans.history = trans.target.kind.name;

//層間轉(zhuǎn)移，則要添加源或目的決定因子sr和tr

if(not isPeer(trans.sState,trans.tState)) then

trans:= changeTrans(trans) ;

TransList = TransList ∪{trans.name × trans.source × trans.sr × trans.event × trans.guard × trans.action × trans.tState × trans.tr × trans.history };

//(2)遞歸處理其他層的region中的transition元素

foreach vertex in self.SubVertex

if(e.isInstanceOf(State)&&e.getType!=”basic_sc”)then

foreach trans in vertex.region.transition

trans.getTransList();

end }

//getStateList方法被織入到Vertex類上

aspect class Vertex{

operation getStateList(TransList)

// self是當前的最頂層狀態(tài)

if(self.isInstanceOf(State))then

entryExit = getEntryExit();

//(1)獲取基本狀態(tài)信息

if(self.getType()==”basic_sc”)then

type = “basic _sc”;

StateList= StateList ∪ {self.name × entryExit × type};

//(2)獲取或狀態(tài)信息

else if(s.getType()==”or_sc”)then

subTrans = getSubTrans(TransList);

subStates = getSubStates();

type = “or_sc”;

StateList= StateList ∪ {self.Name × subStates × 0 × subTrans × entryExit × type};

//遞歸調(diào)用getStateList將當前狀態(tài)的每個子狀態(tài)加入StateList

foreach s in self.subStates

if(not isHistory(s1))then s.getStateList(transList);

//(3)與狀態(tài)轉(zhuǎn)換與或狀態(tài)的處理類似，省略

else if(self.getType()==”and_sc”)then ……

StateList = StateList ∪ {self.Name × subStates × entryExit × type}；

end }

其中，getType()通過判斷狀態(tài)中region的數(shù)目來確定狀態(tài)的類型；chageTrans(trans)用來改變trans的源/目標狀態(tài)，以及設(shè)置源/目標決定因子；isHistory()用來判斷狀態(tài)是否是歷史類型的偽狀態(tài)；getTransList()和getSubStateList()分別用來獲得子狀態(tài)和子轉(zhuǎn)移；Trans2Coq()與State2Coq()的算法相似，限于篇幅未給出算法；Guard2Coq()為bexp中使用的操作符建立了相應(yīng)的解釋器，由解釋器將衛(wèi)式條件轉(zhuǎn)換為相應(yīng)的Coq代碼。

2.3序列圖轉(zhuǎn)換規(guī)則和算法

序列圖的抽象語法定義主要處理的語法單元包括LifeLine、 Event、 Message、Fragment等。首先在Coq中為這些元素定義抽象語法，也使用歸納類型來定義序列圖：

Inductive kind:Set:= | Send:kind | Receive:kind.

Notation ″!″:= Send

Notation ″?″:= Receive

Definition signal:= string.

Definition lifeline:= string.

Definition event:= kind * signal * lifeline * lifeline.

Inductive id:Set:= Id:nat-> id.

(*衛(wèi)式條件的定義*)

Inductive cnd:Type:= | Bvar:id-> cnd | Btrue:cnd

|Bfalse:cnd | Bnot:cnd-> cnd | Band:cnd-> cnd-> cnd

|Bor:cnd-> cnd-> cnd | Bimp:cnd-> cnd-> cnd.

(*序列圖的抽象語法定義*)

Inductive seqDiag:Set:=

|Dtau:seqDiag

|De:event-> seqDiag

|Dpar:seqDiag-> seqDiag-> seqDiag

|Dalt:cnd-> seqDiag-> seqDiag-> seqDiag

|Dopt:cnd-> seqDiag-> seqDiag

|Dstrict:seqDiag-> seqDiag-> seqDiag

|Dloop:nat-> cnd-> seqDiag-> seqDiag.

其中Event中的事件類型分為發(fā)送事件和接受事件，分別用‘?’和‘!’表示。序列圖被表示成一個歸納類型，可以為空(Dtau)，可以通過事件(De)構(gòu)成，也可以是通過交互操作符構(gòu)成。這里只考慮五種交互操作符Dalt、Dopt、Dstrict、Dloop和Dpar。

元模型層面上的序列圖到Coq形式規(guī)范的轉(zhuǎn)換規(guī)則主要包括：

(1) 消息名和生命線名在Coq中都用字符串來表示，分別對應(yīng)signal和lifeline類型；

(2) 序列圖中的每個事件被映射成Coq抽象語法中定義的類型、消息名、接受/發(fā)送生命線組成的四元組；

(3) 消息的約束條件被映射為cnd中規(guī)定的類型中的一種，并且約束條件中的變量被映射為自然數(shù)類型的id；

(4) 利用前面3條規(guī)則，將序列圖映射為由抽象語法中事件，約束條件和五種交互操作符遞歸構(gòu)造的Coq規(guī)范。

序列圖模型到Coq形式規(guī)范轉(zhuǎn)換的算法，與狀態(tài)圖的轉(zhuǎn)換相似，由于要處理的語法單元相對較少，因此去掉了存儲模型中元素的步驟。算法如下：

算法2

//下述方法織入到元模型最頂層類SeqModel上

operation toCoq():String

result:String;

//將依賴于消息的發(fā)送和接受事件，轉(zhuǎn)換為coq代碼

foreach m in message

result = result + m.message2Coq();

//將每個fragment轉(zhuǎn)換為Coq代碼。

foreach f in fragment

result = result + f.fragment2Coq();

return result;

end

//下述方法織入到Message類上

operation message2Coq():String

mName = self.name;

//獲得發(fā)送和接受消息的生命線(lifeline)

sLineName = getSendLineName();

rLineName = getRecLineName();

//發(fā)送事件

sendEvent=write2Coq(“!”,mName,sLineName,rLineName );

//接受事件

recEvent = write2Coq(“?”,mName,sLineName,rLineName );

return sendEvent + recEvent;

end

//下述方法織入到InteractionFragment類上

operation fragment2Coq():String

//(1)當fragment為事件類型時，將發(fā)送接受事件轉(zhuǎn)換

if(self.isInstanceOf(OcreenceSpecification))then

if(self.type ==”send”)then

result = result + event2Coq(self.name,“send”);

else if(self.type ==”receive”)then

result = result + event2Coq(self.name,“receive”);

//(2)當fragment為組合片段類型時

else if(self.isInstanceOf(CombinedFragment))then

//當交互操作符為單元操作符opt時

if(self.operand == “opt”)then

result = result + CombinetoCoq (operand,self.name);

//當為其他四種二元操作符時

else

leftOp = self;

//右操作符為下一個fragment

rightOp = nextFragment;

result = result + Combine2Coq(operand,leftOp,rightOp);

//對組合片段的子片段進行轉(zhuǎn)換

foreach f in self.operand.fragment

result = result + f.fragment2Coq();

return result;

end

算法中event2Coq()實現(xiàn)將某個發(fā)送或接受事件類型的組合片段轉(zhuǎn)換為Coq代碼；Combine2Coq則實現(xiàn)將包含單元或者二元操作符的組合片段轉(zhuǎn)換為Coq代碼。

3　實例研究

根據(jù)轉(zhuǎn)換框架和算法，我們實現(xiàn)了UML動態(tài)子圖到Coq代碼轉(zhuǎn)換的原型工具，實現(xiàn)了轉(zhuǎn)換過程的自動化。本章以用戶在自動取款機(ATM)取款的情景為例，繪制了圖4和圖5所示的序列圖模型和狀態(tài)圖模型，用來對原型工具進行測試。

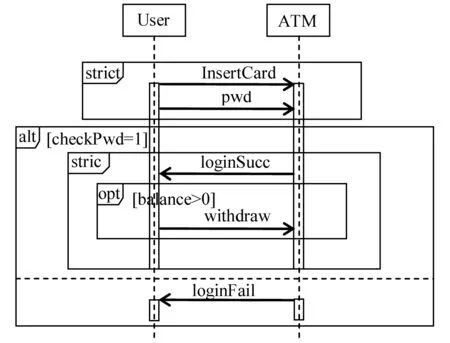
圖4　序列圖模型實例

圖4是用戶在ATM上取款的簡化的交互場景的序列圖。用戶首先插入銀行卡，然后輸入密碼，由ATM機根據(jù)輸入的信息進行身份驗證，發(fā)送驗證成功(loginSucc)或驗證失敗(loginFail)的消息；如果登錄成功，且?guī)粲囝~大于零，用戶可以選擇進行一次取款操作。原型工具執(zhí)行后自動轉(zhuǎn)換生成如下的Coq形式規(guī)范代碼：

Definition C1:cnd:= BEq(AId checkPwd)(ANum 1).

Definition C2:cnd:= BGt(AId balance)(ANum 0).

Definition sInsertCard:event:= (!,″InsertCard″,″User″,″ATM″).

Definition rInsertCard:event:= (?,″InsertCard″,″User″,″ATM″).

Definition spwd:event:= (!,″pwd″,″User″,″ATM″).

Definition rpwd:event:= (?,″pwd″,″User″,″ATM″).

Definition sloginSucc:event:= (!,″loginSucc″,″ATM″,″User″).

Definition rloginSucc:event:= (?,″loginSucc″,″ATM″,″User″).

Definition swithdraw:event:= (!,″cmd″,″User″,″ATM″).

Definition rwithdraw:event:= (?,″cmd″,″User″,″ATM″).

Definition sloginFail:event:= (!,″loginFail″,″ATM″,″User″).

Definition rloginFail:event:= (?,″loginFail″,″ATM″,″User″).

Definition ExampleSeq:SeqDiag:= Dstrict

(Dstrict (Dstrict (De sInsertCard)(De rInsertCard))

(Dstrict (De spwd)(De rpwd)))

(Dalt C1 (Dstrict(Dstrict (De sloginSucc)(De rloginSucc))

(Dopt C2 (Dstrict (De scmd)(De rcmd))))

(Dstrict (De sloginFail)(De rloginFail))).

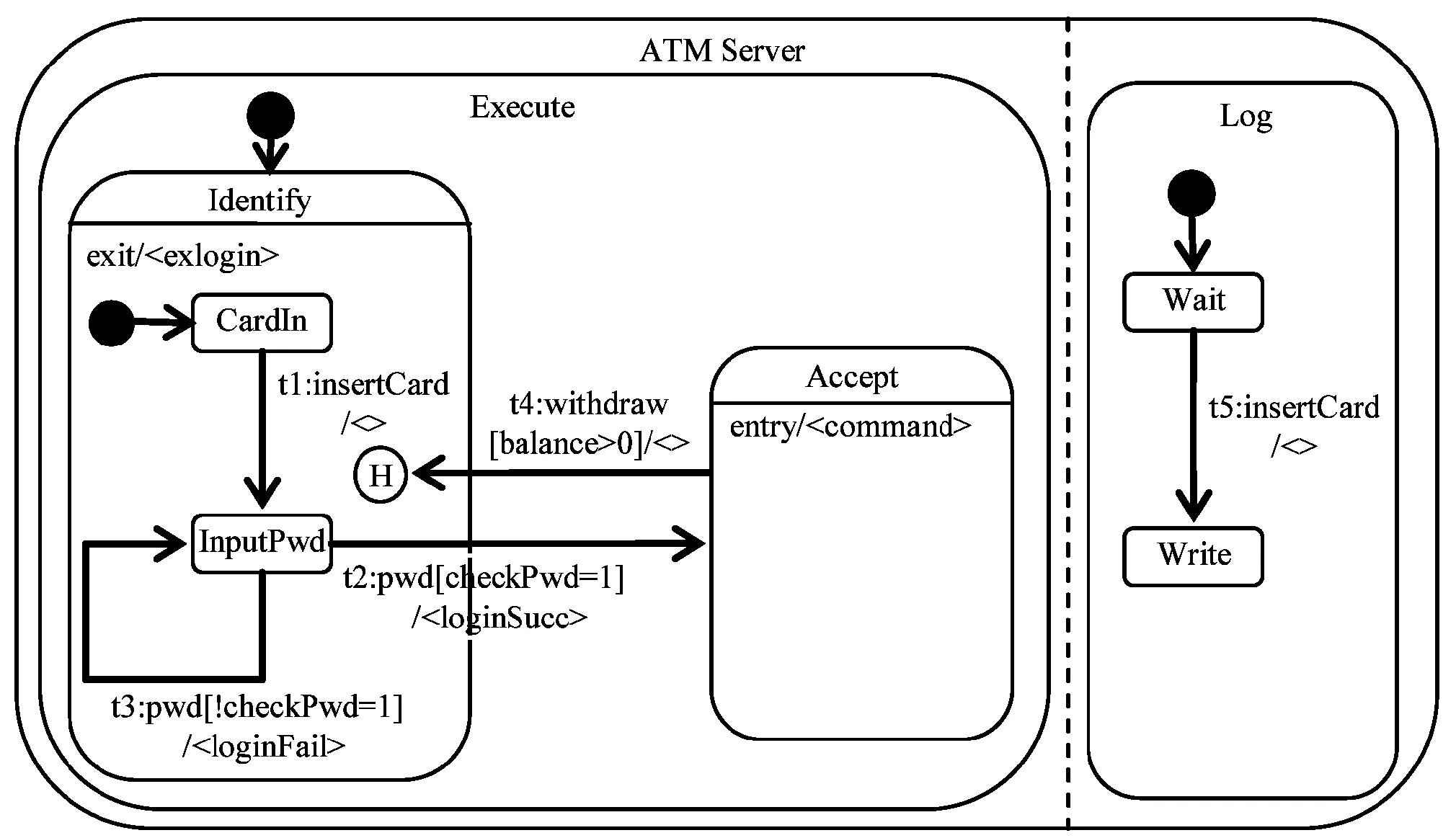
圖5　狀態(tài)圖模型實例

圖5是用戶在ATM上取款時，ATM服務(wù)器狀態(tài)變化情況的狀態(tài)圖。Execute和Log是并行運行的或狀態(tài)，分別表示系統(tǒng)處于給用戶提供服務(wù)的執(zhí)行狀態(tài)，以及系統(tǒng)在進行日志記錄操作的狀態(tài)。原型工具執(zhí)行后轉(zhuǎn)換為如下Coq形式規(guī)范代碼：

Definition g0:guard:= BGt (AId balance) (ANum 0).

Definition g1:guard:= BEq (AId checkPwd) (ANum 1).

Definition g2:guard:= BNot (BEq (AId checkPwd) (ANum 1)).

Definition t4:trans:=

(″t4″,1,nil,″withdraw″,g0,nil,nil,0,shallow).

Definition t1:trans:=

(″t1″,0,nil,″insertCard″,BTrue,nil,nil,1,none).

Definition t2:trans:= (″t2″,0,(″Indentify″::″InputPwd″::nil),

″pwd″,g1,″loginSucc″::nil,nil,1,none).

Definition t3:trans:=

(″t3″,1,nil,″pwd″,g2,″loginFail″::nil,nil,1,none).

Definition t5:trans:=

(″t5″,0,nil,″insertCard″,BTrue,nil,nil,1,none).

Definition n0:sc:= basic_sc ″CardIn″ (nil,nil).

Definition n1:sc:= basic_sc ″InputPwd″ (nil,nil).

Definition n2:sc:= or_sc ″Indentify″ (n0::n1::nil) 0

(t1::t3::nil) (nil,″exlogin″::nil).

Definition n3:sc:= basic_sc ″Accept″ (″command″::nil,nil).

Definition n4:sc:=

or_sc ″Execute″ (n2::n3::nil) 0 (t4::t2::nil) (nil,nil).

Definition n5:sc:= basic_sc ″Wait″ (nil,nil).

Definition n6:sc:= basic_sc ″Write″ (nil,nil).

Definition n7:sc:=

or_sc ″Log″ (n5::n6::nil) 0 (t5::nil) (nil,nil).

Definition n8:sc:= and_sc ″ATMServer″ (n4::n7::nil) (nil,nil).

這些自動生成的Coq形式規(guī)范代碼，可以在定理證明器Coq中直接打開，進行下一步的分析和驗證，使之前的研究工作[6，7]更加完善。本文完整源代碼和實例可在文獻[10]中下載。

4　相關(guān)工作

國內(nèi)外將形式化方法應(yīng)用于UML的研究一直是熱點。較多的工作致力于類圖的形式化和驗證，如文獻[12]等。對于UML的典型動態(tài)子圖——序列圖和狀態(tài)圖，也有許多形式語義研究工作，可參見綜述文獻[13，14]。本節(jié)主要討論將UML動態(tài)子圖轉(zhuǎn)換為形式規(guī)范的相關(guān)工作。

文獻[15，16]都將UML狀態(tài)圖轉(zhuǎn)換為了B語言規(guī)范，但是文獻[15]中沒有將狀態(tài)內(nèi)部的動作考慮在內(nèi)，且只對簡單的狀態(tài)圖進行了分析。在文獻[16]中為了表示狀態(tài)圖中的事件和轉(zhuǎn)移，加入了自己定義的新標簽，這就使得轉(zhuǎn)換得到的B語言規(guī)范不符合標準的B語言抽象語法。本文的狀態(tài)圖語法定義全面完整，并且生成的Coq規(guī)范也符合目標抽象語法。文獻[17]實現(xiàn)了UML狀態(tài)圖到Petri網(wǎng)的轉(zhuǎn)換，但是整個轉(zhuǎn)換都在模型層面進行，不能保證轉(zhuǎn)換前后語法的一致性。

文獻[18]基于B方法對用例圖模型與序列圖模型進行形式化轉(zhuǎn)換，提出了轉(zhuǎn)換規(guī)則，但沒有實現(xiàn)自動轉(zhuǎn)換工具。文獻[19] 采用了和本文相似的元模型層面的轉(zhuǎn)換框架，將序列圖和狀態(tài)圖轉(zhuǎn)換為廣義隨機Petri網(wǎng)，但是也只考慮了基本元素的轉(zhuǎn)換，對序列圖沒有考慮組合片段的情況，對狀態(tài)圖沒有考慮歷史偽狀態(tài)的轉(zhuǎn)換。本文則在全面考慮各種元素的轉(zhuǎn)換規(guī)則的基礎(chǔ)上，實現(xiàn)了自動化的轉(zhuǎn)換工具，由于利用了Kermeta的面向方面編程特性，規(guī)則的修改和擴展也很容易。

5　結(jié)　語

本文提出了一種元模型層次的UML動態(tài)子圖到Coq形式規(guī)范的轉(zhuǎn)換框架。首先給出了狀態(tài)圖和序列圖形式化Coq抽象語法，然后提出元模型層面轉(zhuǎn)換規(guī)則，并最終實現(xiàn)從UML動態(tài)子圖到Coq形式規(guī)范轉(zhuǎn)換的原型工具。本文的工作，使得從UML動態(tài)子圖到Coq規(guī)范的自動轉(zhuǎn)換成為現(xiàn)實，保證了轉(zhuǎn)換前后語法的正確性，得到了符合目標抽象語法的Coq形式規(guī)范，為分析驗證工作提供了便利。下一步的工作是完善現(xiàn)有工作中UML狀態(tài)圖和序列圖的特性，為實際應(yīng)用提供更全面的支持。

[1] Rumbaugh J,Jacobson I,Booch G.Unified Modeling Language Reference Manual[M].The Pearson Higher Education,2004.

[2] Paulin-Mohring C.Introduction to the Coq proof-assistant for practical software verification[C]//Tools for Practical Software Verification.Springer Berlin Heidelberg,2012:45-95.

[3] Leroy X.Formal verification of a realistic compiler[J].Communications of the ACM,2009,52(7):107-115.

[4] Chlipala A.A verified compiler for an impure functional language[C]//Proceedings of the 37th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages,2010,45(1):93-106.

[6] Zuo Y,Dou L,Xu L,et al.Mechanized semantics of UML sequence diagrams[C]//Proceedings of the IASTED International Conference on Engineering and Applied Science,2012:188-195.

[7] Dou L,Lu L,Yang Z,et al.Towards mechanized semantics of UML sequence diagrams and refinement relation[C]//Proceedings of the 24th IASTED International Conference on Modelling and Simulation,2013:262-269.

[8] Kermeta[EB/OL].[2015-3-1].http://www.kermeta.org/.

[9] Cetinkaya D,Verbraeck A.Metamodeling and model transformations in modeling and simulation[C]//Proceedings of the Winter Simulation Conference.Winter Simulation Conference,2011:3048-3058.

[10] Bertot Y,Castéran P.交互式定理證明與程序開發(fā):Coq 歸納構(gòu)造演算的藝術(shù)[M].顧明等譯.清華大學出版社,2010.

[11] 元模型層次的UML動態(tài)子圖到Coq形式規(guī)范的轉(zhuǎn)換工具源代碼及案例[EB/OL].[2015-3-1].https://github.com/lisa-dou/UML2Coq.

[12] Lano K,Clark D,Androutsopoulos K.UML to B:Formal verification of object-oriented models[C]//Integrated Formal Methods.Springer Berlin Heidelberg,2004:187-206.

[13] Micskei Z,Waeselynck H.The many meanings of UML2 Sequence Diagrams:a survey[J].Software & Systems Modeling,2011,10(4):489-514.

[14] Lund M S,Refsdal A,Stφlen K.Semantics of UML Models for Dynamic Behavior[M]//Model-Based Engineering of Embedded Real-Time Systems.Springer Berlin Heidelberg,2010:77-103.

[15] Ledang H,Souquières J.Contributions for modelling UML state-charts in B[C]//In Integrated Formal Methods,Springer Berlin Heidelberg,2002:109-127.

[16] Idani A,Ledru Y.Dynamic graphical UML views from formal B specifications[J].Information and Software Technology,2006,48(3):154-169.

[17] Pais R,Gomes L,Barros J P.From UML state machines to Petri nets:History attribute translation strategies[C]//IECON 2011-37th Annual Conference on IEEE Industrial Electronics Society.IEEE,2011:3776-3781.

[18] 夏志翔,徐中偉,陳祖希,等.UML模型形式化B方法轉(zhuǎn)換的實現(xiàn)[J].計算機應(yīng)用與軟件,2011,28(11):15-20.

[19] Bernardi S,Donatelli S,Merseguer J.From UML sequence diagrams and statecharts to analysable petri net models[C]//Proceedings of the 3rd international workshop on Software and performance.ACM,2002:35-45.

A METAMODELLING LEVEL TRANSFORMATION FROM UML DYNAMIC SUB-DIAGRAMS TO COQ

Dou LiangYin Min*Li ChaoYang Zongyuan

(DepartmentofComputerScienceandTechnology,EastChinaNormalUniversity,Shanghai201100,China)

UML dynamic sub-diagrams mainly comprise the sequence diagram and the state machine diagram,they are widely applied in describing system behaviours.However,it is hard to perform direct formal verification due to the semi-formal semantics of UML.Coq is a mainstream interactive theorem prover,using formal Coq specification to describe UML dynamic sub-diagrams model can carry out verification on model’s attributes on that basis.According to our previous work,the paper presents a framework to transform UML dynamic sub-diagrams model to Coq formal specifications,and the transformation rules of UML sequence diagram and state machine diagram are offered at meta-modelling level.The algorithm and the implementation of prototype tool are also introduced.This metamodelling level transformation framework ensures the correctness of semantics before and after transformation,and lays the basis for further analysis and verification.

UMLDynamic diagramsModel transformationMetamodellingCoqKermeta

2015-04-03。國家自然科學基金項目(61070226)。竇亮，講師，主研領(lǐng)域：形式化方法，定理證明和軟件工程。尹敏，講師。李超，碩士生。楊宗源，教授。

TP311

A

10.3969/j.issn.1000-386x.2016.08.002