新建鐵路隧道上跨既有公路隧道控制爆破安全距離研究
趙豐,薛亞東,李碩標 ,趙瀚翔
(1. 同濟大學 巖土及地下工程教育部重點實驗室,上海 200092;2. 同濟大學 地下建筑與工程系,上海 200092)
?

新建鐵路隧道上跨既有公路隧道控制爆破安全距離研究
趙豐1, 2,薛亞東1, 2,李碩標1, 2,趙瀚翔1, 2
(1. 同濟大學 巖土及地下工程教育部重點實驗室,上海 200092;2. 同濟大學 地下建筑與工程系,上海 200092)
新建塔石嶺鐵路隧道上跨既有公路隧道,采用全斷面爆破施工,為了確保既有公路隧道運營的安全,需要明確控制爆破開挖的安全施工距離。基于已有的巖體中爆破振動速度衰減理論模型,首先計算安全施工距離范圍,為驗證模型與參數的合理性,開展相應的有限元計算分析。計算結果得出了爆破距離與既有隧道襯砌拱頂振動速度的關系,據此可根據振動速度安全標準計算得到相應的爆破施工安全距離,從而為工程爆破設計提供科學依據。
交叉隧道;控制爆破;安全距離
隨著我國交通運輸事業的迅猛發展,越來越多的隧道工程投入建設。在近距離交叉隧道爆破施工對既有隧道的影響方面,國內外學者做了大量研究[1-3],采用數值模擬的方法對爆破過程中既有隧道的振動響應做了詳細分析[4-6],但對于上跨隧道控制爆破安全距離的研究還比較少。在保證既有隧道運營安全的前提下,如何合理控制上跨隧道控制爆破施工的距離對縮短工程工期、減少工程造價有著直接的影響。

臨近工程爆破不可避免會對既有的巖石產生振動影響,振動沖擊波可能導致隧道結構發生損壞或者出現襯砌掉塊,嚴重威脅隧道運營安全[8]。對于爆破振動的影響評價因素(或指標),許多國家,如中國、美國、德國、瑞典等,采用質點振動速度作為衡量爆破振動效應的標準。大量現場試驗和觀測表明,爆破振動破壞程度與質點速度的相關性最好,且與其他物理量相比,振速與巖土性質有較穩定的關系[9],因而學者提出了施工控制的重點是爆破振動的影響[10-13]。有關爆破振動速度的研究,目前主要有實測法、經驗公式法以及數值模擬法等。考慮爆破設計的安全與合理,本文通過理論分析計算上跨隧道的安全施工距離,并通過數值模擬,分析不同爆破工況下既有隧道二次襯砌控制點的振速變化規律,從而把握新建隧道控制爆破施工的安全距離范圍[11]。
1 工程概況
擬建塔石嶺隧道位于浙江省龍泉市龍泉鎮境內,為鐵路單線單洞隧道,隧道全長3672.89m,斷面底寬7.6m,高8.5m,受路線的總體走向和地形地貌等條件控制,該隧道設計路線在里程DK151+185處上跨既有公路(S228省道)坑底嶺隧道,坑底嶺隧道底寬11m,高7m,兩隧道呈64°斜交,最短垂直距離為17m,交叉處地質條件為Ⅲ級圍巖,具體如圖1所示。為了減少對既有隧道的影響,需要在兩隧道交叉點處一定范圍內進行控制爆破,綜合考慮造價、工期等各方面因素,控制爆破安全距離的選取是工程設計的關鍵。
2 理論分析
根據《爆破安全規程》(GB6722-2011)[7],對于交通隧道,規定安全振動速度應小于15cm/s。考慮到既有隧道已運營多年,襯砌強度有所下降,且隧道交叉區域附近存在斷層構造,因此建議本工程既有隧道襯砌的振動速度不大于5cm/s。
對于爆破振動波在傳播過程中的衰減規律已有如下研究:
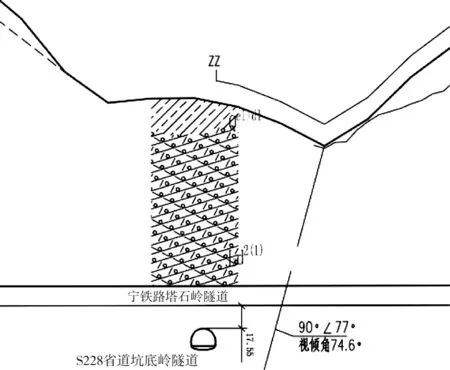
圖1 隧道位置剖面圖Fig.1 Cross section of tunnel position
1)薩道夫斯基公式
蘇聯科學家薩道夫斯基由試驗歸納出與巖石介質性質、爆源有關的系數K和衰減指數α,得到目前工程爆破計算地面振動速度普遍采用的經驗公式:
(1)
式中:v為地面質點峰值振動速度(cm/s); Q為爆破裝藥量kg;齊發爆時取為總藥量,分段爆破時取為最大一段藥量;R為測點距爆源中心的距離m;K為與巖石性質、爆破參數和方法有關的系數;a為爆破振動波隧距離衰減的指數。
我國《爆破安全規程》[7]列出了K和a的計算選取范圍(見表1)。K和a的取值也可以通過不同巖石的類型選取[8]。

表1 K 值和α值與巖石的關系
2)美國礦業局對20個采石場和建設工地的爆破振動觀測數據進行了分析,提出了振速的計算公式:
(2)
式中:K和α分別為現場的特征系數和衰減指數,其他符號意義同前。
3)P.B.Attwell(奧特維爾)等人對歐洲采石場的爆破振動觀測數據進行了統計分析,提出的振速公式如下:
v=K(Q/R2)α
(3)
式中符號意義同前。
4)日本旭化成工業株式會社提出:
(4)
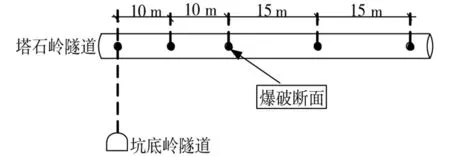
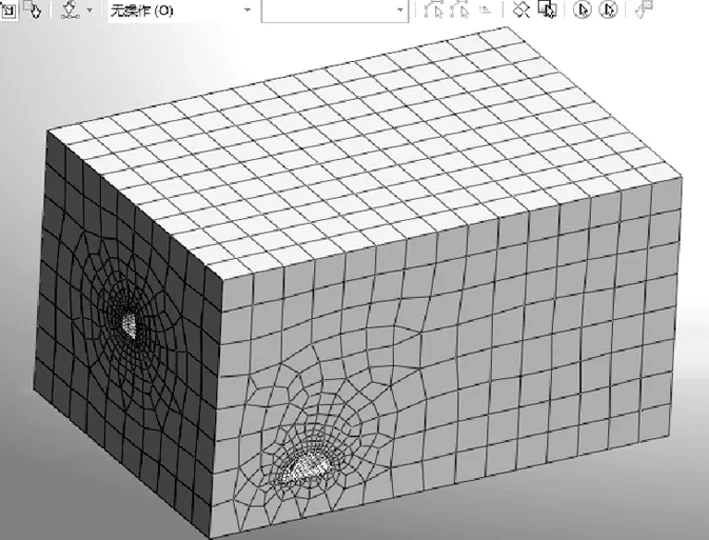
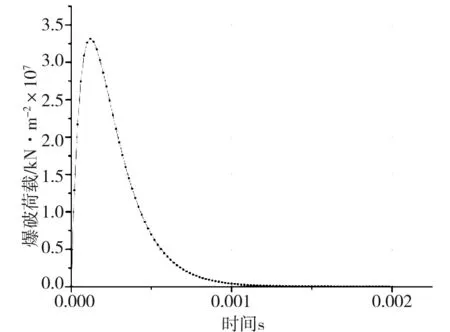
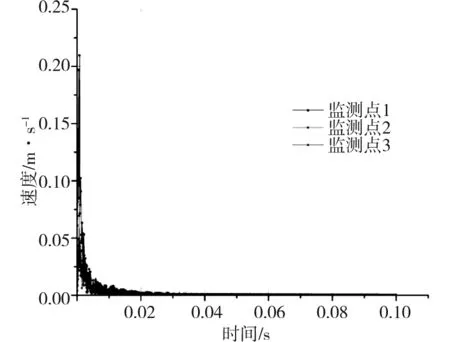
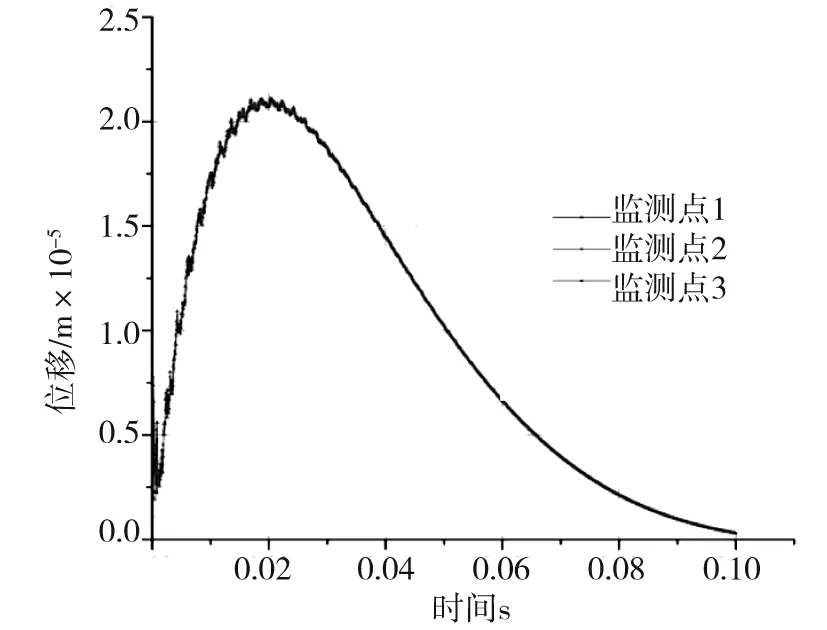
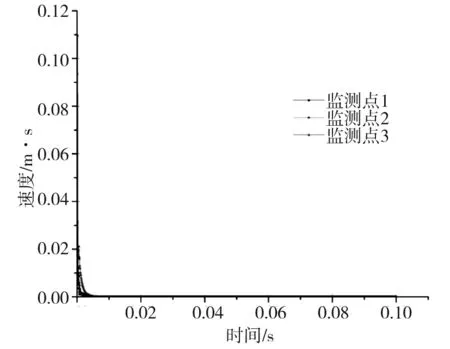
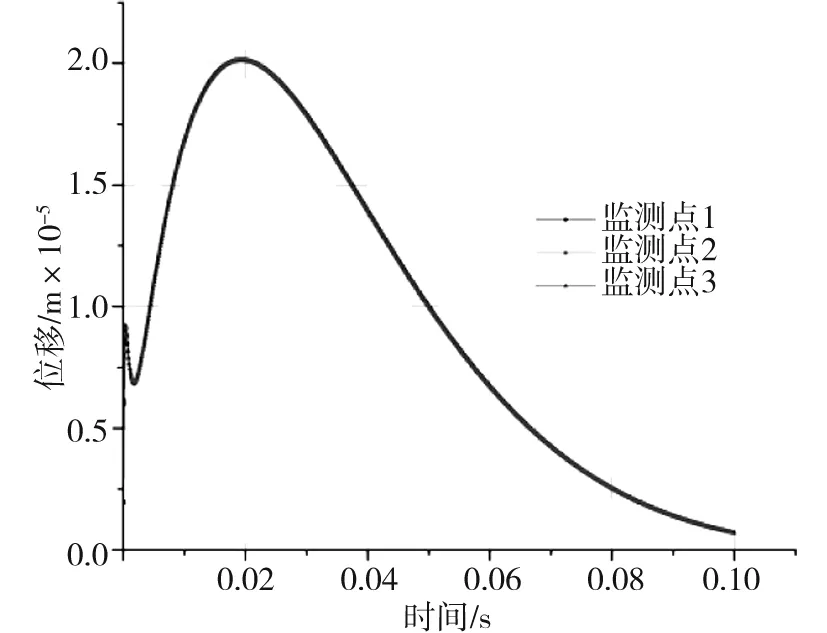
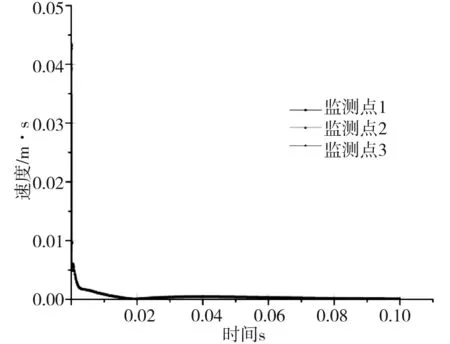
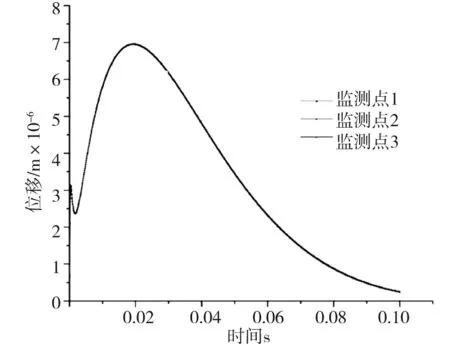
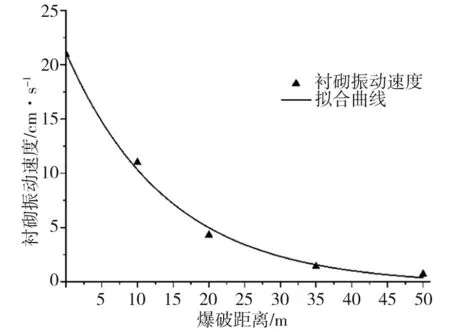
式中:K是與爆破條件、地質條件有關的系數,掏槽爆破時,K=500~1 000;臺階爆破時K=200~500;α為指數,爆區為黏土層時α=2.5~3.0,爆區巖石時,α=2.0;R為測點距爆源中心的距離m,30m 根據建議標準,控制既有隧道二次襯砌的振動速度為5cm/s。交叉處地質條件為Ⅲ級圍巖,參考表1可得到K與α的取值范圍,根據現場的鉆孔資料以及在現場所做的地層聲波測試[12],并結合以往的工程經驗,可大致估計所在地層的完整性。本工程計算參數取值如下:K=200~220,α=1.6,該工程分段爆破最大單段藥量為Q=16kg。利用上述4個公式分別反算得到的控制爆破安全距離范圍見表2。 表2 計算得到的控制爆破安全距離 3.1模擬方案 為了進一步研究新建隧道爆破開挖距離對既有隧道的影響,并與已有經驗公式相互驗證,采用MIDAS/GTS/NX大型數值模擬軟件進行模擬計算。根據相關資料和爆破計算理論,分別設置在隧道交叉點正上方開挖、距正上方右側10m開挖、距正上方右側20m開挖、距正上方右側35m開挖和距正上方右側50m開挖五種種模擬方案,每種方案全斷面開挖的進尺為3m。模擬計算方案示意圖見圖2。 圖2 模擬計算方案示意圖Fig.2 Simulation calculation program diagram 3.2有限元模型 根據本工程中隧道的尺寸、間距、以及爆破振動影響的范圍,確定模型長×寬×高=150m×100m×87m,計算模型網格見圖3。 圖3 有限元網格圖Fig.3 FEM model 3.3模型參數 模型中圍巖及隧道襯砌的物理力學參數見表3。 表3 有限元分析參數表 3.4監測點布置 模擬時,在既有公路隧道拱頂的襯砌上沿縱向布置3個監測點,監測新建隧道爆破開挖過程中對既有隧道襯砌的影響,測點間距25m,測點2位于兩隧道交叉處正下方,監測點布置見圖4。 3.5本構模型的選取 Hoke-Brown本構模型廣泛應用于巖石力學工程,但在實踐中所需的擾動因子D和地質強度指標GSI2個參數比較難以準確獲取。利用擾動巖體波速Vp和巖石縱波波速比值的平方計算擾動因子D,利用巖體縱波波速Vp與巖體RMR值的關系來計算巖體的GSI值,推導得到改進后的Hoke-Brown本構模型: 圖4 監測點布置圖Fig.4 Arrangement of monitoring points (5) (6) (7) (8) 定義擾動因子: (9) 式中,σc為巖石的單軸抗壓強度;Vi、Ei和kvi分別為巖體波速、變形模量和完整性系數;V0和E0分別為巖石(巖塊)波速、變形模量。一般情況下,取i=1,V1、E1和kv1分別表示巖體的波速、變形模量和完整性系數;在多次擾動(多次爆破)情況下,取i=2,3,4…n,分別表示在多次(i-1次)擾動后巖體的波速、變形模量和完整性系數等性質。 3.6邊界條件 在數值模擬計算邊界條件方面,有固定邊界,黏性邊界和彈性邊界。結合衢寧鐵路塔石嶺隧道采用爆破施工,爆破振動波對于固定邊界會引起振蕩反射波,導致計算結果失真,因此采用黏彈性邊界較為適合。黏性采用比較通用的瑞利(Rayleigh)阻尼,根據文獻[5]確定臨界阻尼ξmiin=0.01,體系基頻?0=50Hz。 3.7模型加卸荷計算 爆破動載的模擬,通常采用在設置的爆破區域邊界上施加相同當量的爆破動壓力荷載,美國公路研究所(NationalHighwayInstitute(US),1991)建議考慮爆破振動衰減隨時間作用的動壓力公式: (10) (11) 式中:Pdet為爆破荷載kN/m2;PB為作用在孔壁面上的退耦爆破壓力MPa; Ve為爆破速m/s;dc為裝藥直徑mm;dh為裝藥孔直徑mm;Sge為容重kN/m3。 在上述公式的基礎上,考慮時間函數關系,Statfield提出了改進爆破荷載計算公式: (12) 式中:B為荷載系數,為每1kg裝藥量產生的動壓力,可取16 338。單段藥量的荷載見圖5。 圖5 爆破荷載歷程Fig.5 History of blasting load 4.1正上方開挖 塔石嶺隧道掌子面在已建隧道正上方以全斷面法爆破施工,既有隧道襯砌上3個監測點處的振動速度時程曲線如圖6所示。襯砌位移量時程曲線如圖7所示。 圖6 振動速度時程曲線Fig.6 Vibration velocity time history curve 圖7 襯砌位移量時程曲線Fig.7 Lining displacement time history curve 正上方3m進尺全斷面開挖時,既有隧道襯砌振動速度最大值達到20.95cm/s,超過了建議的允許振動速度, 既有隧道襯砌位移最大值達到2.109×10-5,變形不會影響既有隧道安全。 4.2右側10 m開挖 塔石嶺隧道掌子面在已建隧道右側10m處全斷面法爆破施工,既有隧道襯砌上3個監測點處的振動速度時程曲線如圖8所示。襯砌位移量時程曲線如圖9所示。 圖8 振動速度時程曲線Fig.8 Vibration velocity time history curve 正上方右側10m處3m進尺全斷面開挖時,既有隧道襯砌振動速度最大值達到11.00cm/s,超過建議的允許振動速度, 既有隧道襯砌位移最大值達到2.011 5×10-5,變形不會影響既有隧道安全。 4.3右側20 m開挖 塔石嶺隧道掌子面在已建隧道右側20m處全斷面法爆破施工,既有隧道襯砌上3個監測點處的振動速度時程曲線如圖10所示。襯砌位移量時程曲線如圖11所示。 圖9 襯砌位移量時程曲線Fig.9 Lining displacement time history curve 圖10 振動速度時程曲線Fig.10 Vibration velocity time history curve 圖11 襯砌位移量時程曲線Fig.11 Lining displacement time history curve 正上方右側20m處3m進尺全斷面開挖時,既有隧道襯砌振動速度最大值達到4.30cm/s,小于建議的允許振動速度。既有隧道襯砌位移最大值達到7×10-6,不會影響既有隧道安全。 通過數值模擬,可得到不同開挖距離下拱頂襯砌質點的振動速度,如表4所示。 表4 參數值分析 對模擬結果進行擬合,得到爆破距離與振動速度之間的關系曲線,如圖12所示。 圖12 襯砌振動速度與距離的擬合曲線Fig.12 Line of the fitting curve of velocity and distance 該擬合曲線的函數方程為: y=y0+A1e-x/t1 (13) 式中:x為爆破開挖的距離;y為既有隧道拱頂襯砌質點的振動速度;y0,A1和t1為常數,分別為-0.27,21.38和14.25,擬合相似度為0.99。 將理論模型計算的結果與數值分析模擬的結果進行比較,發現用薩道夫斯基計算得到的安全距離與模擬的距離最為接近,而用其他公式計算的距離與模擬有較大的偏差。 1)在正上方爆破開挖時,既有隧道襯砌振動速度的最大值達到20.952cm/s,在正上方右側10m爆破開挖時,既有隧道襯砌振動速度的最大值達到11cm/s,均大于5cm/s;在正上方右側20m爆破開挖時,既有隧道襯砌振動速度的最大值為4.3cm/s,小于5cm/s;在正上方右側35m及50m爆破開挖時既有隧道襯砌振動速度遠小于5cm/s。結合理論分析結果,建議在塔石嶺隧道掌子面距離交叉點20m左右的范圍內施工時,需采用控制爆破的方式以保證既有隧道的安全。 2)通過擬合曲線可得到爆破距離與既有隧道襯砌拱頂振動速度的關系,據此可根據振動速度安全標準計算得到相應的爆破施工安全距離,從而為工程爆破設計提供科學依據。 3)通過實例驗證了爆破振動速度傳播規律采用數值模擬與經驗公式兩種方法計算的合理性與各自的不足,建議在爆破振動分析中結合兩種分析方法以取得可指導實踐的結論。 [1] 葉培旭, 楊新安, 凌保林, 等. 近距離交叉隧洞爆破對既有隧道的振動影響[J]. 巖土力學, 2011, 32(2): 537-541 . YEPeixu,YANGXinan,LINBaolin,etal.Vibrationeffectsonexistingtunnelinducedbyblastingofanadjacentcrosstunnel[J].RockandsoilMechanics, 2011, 32(2): 537-541. [2]YANGRL,ROCQUEP,KATSABANISP,etal.Measurementandanalysisofnear-filedblastvibrationanddamage[J].GeotechnicalandGeologicalEngineering,1994,12:169-182. [3]Jong-HoShin,Hoon-GiMoon,Sung-EunChae.Effectofblast-inducedvibrationonexistingtunnelsinsoftrocks[J].TunnelingandUndergroundSpaceTechnology,2011,26:51-61. [4] 喬汝佳. 小凈距爆破作用下隧道的動力響應研究 [D]. 西安: 西安建筑科技大學, 2013 . QiaoRujia.Studyoninfluenceofblastingvibrationontunnelsmallclearance[D].Xi’an:Xi’anUniversityofArchitectureandTechnology, 2013. [5] 潘小馬. 臨近隧道施工對既有隧道的影響[D]. 成都: 西南交通大學, 2002: 26 - 27. PanXiaoma.Influenceofanewtunnelconstructionontheadjacentexistingtunnel[D].Chengdu:SouthwestJiaotongUniversity,2002:26-27. [6] 醋經緯. 小凈距交叉隧道爆破振動控制技術研究 [D]. 蘭州: 蘭州交通大學, 2014. CuJingwei.Researchonthecontroltechnologyofsmallcleardistancecrosstunnelblastingvibration[D].Lanzhou:LanzhouJiaotongUniversity, 2014. [7]GB6722—86,爆破安全規程[S]. GB6722—86,Blastingsafetyregulation[S]. [8] 周維垣. 高等巖石力學[M]. 北京: 水利水電出版社, 1989. ZHOUweiyuan.Advancedrockmechanics[M].Beijing:Water&PowerPress, 1989. [9] 汪旭光. 爆破設計與施工[M]. 北京: 冶金工業出版社, 2012. WANGxuguang.Blastingdesignandconstruction[M].Beijing:MetallurgicalIndustryPress, 2012. [10] 陳仕猛. 上下交叉隧道近接施工技術的研究[D].成都: 西南交通大學, 2008. CHENShimeng.Studyonconstructionschemeofup-down-crossingandsmallclear-spantunnels[D].Chengdu:SouthwestJiaotongUniversity, 2008. [11] 趙東平, 王明年. 小凈距交叉隧道爆破振動響應研究[J]. 巖土工程學報, 2007, 29(1): 116-119. ZHAODongping,WANGMingnian.Studyoninfluenceofblastingvibrationoncrosstunnelswithsmallclearance[J].ChineseJournalofGeotechnicalEngineering, 2007, 29(1): 116-119 . [12] 閆長斌, 徐國元, 楊飛. 爆破動荷載作用下圍巖累計損失效應聲波測試研究[J]. 巖土工程學報, 2007, 29(1): 88-92. YANGChangbin,XUGuoyuan,YANGFei.Measure-mentofsoundwavestostudycumulativedamageeffectonsurroundingrockunderblastingload[J].ChineseJournalofGeotechnicalEngineering, 2007, 29(1) : 88-92. [13] 李玉峰, 彭立敏, 雷明鋒. 交叉隧道工程設計施工技術研究進展[J]. 鐵道科學與工程學報, 2014, 11(1): 67-78. LIyufeng,PENGlimin,LEImingfeng.Researchprogressinthedesignandconstructiontechnologyofcrossingtunnel[J].JournalofRailwayScienceandEngineering, 2014, 11(1): 67-78. Analysis on control blasting safety distance of the new railway tunnel overpasses the established highway tunnel ZHAO Feng1, 2,XUE Yadong1, 2,LI Shuobiao1, 2,ZHAO Hanxiang1, 2 (1.KeyLaboratoryofGeotechnicalandUndergroundEngineering(TongjiUniversity),MinistryofEducation,Shanghai200092,China;2.DepartmentofGeotechnicalEngineeringCollegeofCivilEngineering,TongjiUniversity,Shanghai200092,China) ProposedTashilingrailwaytunneloverpassestheestablishedhighwaytunnelandisdesignedtoadoptthewholesectionblastingconstruction.Inordertoensurethesafetyoftheexistinghighwaytunneloperation,itisnecessarytodefinethesafetyconstructionofcontrolledblastingexcavationdistance.Basedontheexistingtheoreticalmodelofblastingvibrationvelocityattenuationinrockmass,itwasthefirsttocalculatethesafetyconstructionoftheprojectscope.Next,thecorrespondingfiniteelementcalculationandanalysiswereusedtoverifytherationalityofthemodelandparameter.Theresultsindicatetherelationshipbetweenexplosiondistanceandthevibrationvelocityofthetunnelvaultlining.Accordingtothesafetystandardsofvibrationvelocity,thecorrespondingblastingconstructionsafetydistancecanbeobtainedthroughcalculation,soastoprovidescientificbasisforengineeringblastingdesign. crossedtunnel;controlblasting;safetydistance 2015-08-12 浙江省交通廳科技資助項目(2015J22) 薛亞東(1971-),男,山西芮城人,副教授,博士,從事隧道及地下工程研究;E-mail:yadongxue@126.com TU455 A 1672-7029(2016)07-1365-07
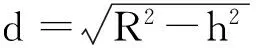
3 數值模擬

4 計算結果及分析

5 結論

