基于FPGA的進位保留Barrett模乘法器設計與實現

車文潔，高獻偉

（北京電子科技學院 北京 100070）

基于FPGA的進位保留Barrett模乘法器設計與實現

車文潔，高獻偉

（北京電子科技學院 北京 100070）

在有限域上的模算術運算中，乘法運算最基礎且最耗時，因此為提高公鑰密碼體質的運算速度，設計出運算速度快、消耗時間少的模乘法器非常關鍵。該文設計出進位保留Barrett模乘法器，乘法部分利用進位保留乘法器，求模運算部分利用Barrett約減運算，用硬件描述語言進行FPGA設計與實現，避免了除法運算。對于192位的操作數，完成Barrett模乘需要約186個時鐘周期，計算速率可以達到269.17 Mb/s。

Barrett模約減；Barrett模乘法器；FPGA；硬件描述語言

作為目前最受歡迎的公鑰密碼算法，ECC具有傳輸帶寬少、處理速度快、存儲空間占用小、靈活性高及安全性好等優點［1］，公鑰密碼算法均以模算術運算為基本運算，其操作數通常是大整數，運算量較大、耗時多，模算術運算的效率決定了公鑰密碼系統的運行效率，設計出高效模乘法器一直是公鑰研究領域的關注焦點，本文設計出的模乘法器運算速度高，耗時較少，在公鑰密碼系統有較高的實用性。

1 進位保留并行乘法器

利用進位保留并行乘法器原理，得出電路圖如圖1所示。

該結構圖由1×1乘法器的n×m陣列組成，其耗時等于n·T（1，1）加上m位輸出加法器的延時。關鍵路徑如上圖陰影部分所示。其計算時間等于

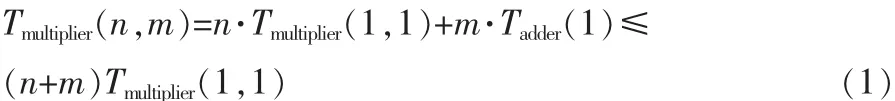
2 Barrett模約減運算

即使m不屬于非特殊形式的模數，xmodm的計算仍屬于模運算，屬于模乘運算中較耗時的部分。由于域乘法的速度是ECC算法的運算速度快慢的關鍵，因此選擇模很重要。

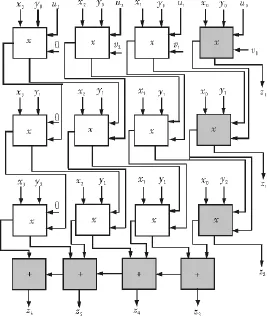
圖1 進位保留并行乘法器Fig.1 Carry-save combinational multiplier

Barrett方法［2-4］利用模約減運算代替了高成本的除法。如果使用模約減方法直接代替一般的模運算，則需要一種高成本的與模相關的的計算，因此本文中的設計方法適用于對一個模的多次約減運算。

假設Bk-1＜m＜Bk，其中B是基（B通常是2或2的冪）。如果m是B的冪，計算很簡單。z=xmodm的值是m整除x所得的余數，也就是

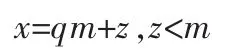
Barrett算法首先計算q=?x/m」的近似值q′，因此

首先計算（隨后計算q的近似值q′）

因為z=x-qm，由式（2）和式（3）得

令t為使

的最小整數，則

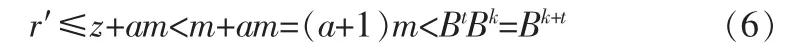
故

又由式（3）得出

下面的算法用于計算（k+T）比特數r=xmodm，其中包括計算q=?x/m」的近似值q′的approximation函數。

算法2.1 n-digit to（k+t）-digit約減

q:=approximation（x，m）；//q=?x/m」的近似值q′

r:=（（x mod Bk+t）-（q*m mod Bk+t））mod Bk+t；//計算 （k+T）比特數r=xmodm

如果a=2且B≥3，則式（5）中Bt≥3且t=1時等式成立。因而，可用modBk+1來計算x-q′m，該情況與經典的Barrett算法相對應。

下面我們給出計算q的近似值q′的一種方法［5］。

把x和m用基B表示為

q=?x/m」的近似值q′是

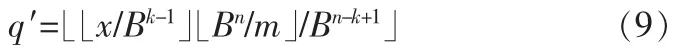
可以看到

此外

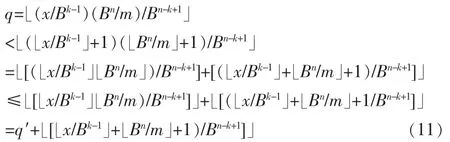
又因x＜Bn且m≥Bk-1則

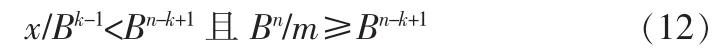
于是

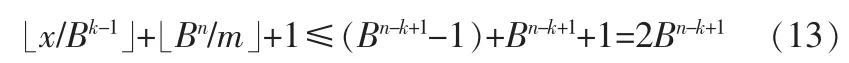
由式（11）和式（12）得出

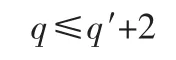
相當于

根據式（5）和式（14），t的值要符合Bt≥3，因此

若B=2，則t=2（估算時運算modBk+2），

若B＞2，則t=1（估算時運算modBk+1）。

綜上總結，可得出計算z=xmodp的算法2.2，其中，常數c必需提前計算，如式（15）。

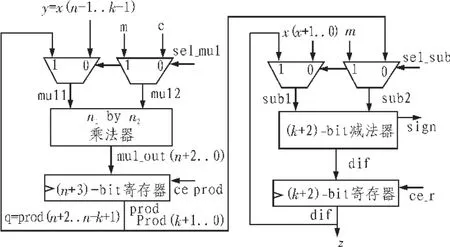
圖2 Barrett約減算法的數據路徑（B=2）Fig.2 Datapath of a Barrett reducer

B=2時Barrett約減的數據路徑對應圖2所示。圖中乘法器的輸入值mul1與mul2的大小取決于n與k的相對值：y 和c是（n-k+1）-bit數，q是（k+2）-bit數，m是k-bit數，因此

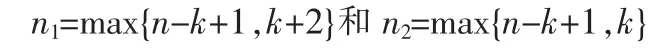
所述時鐘信號的最小周期值是n1-bit×n2-bit乘法器的延遲，上述乘法器僅使用了（n+3）個輸出。若使用進位保留乘法器，則相應消耗時間約為（n+3）TMULT。由式（6）和式（14），且r′＜3m，則得出最終計算結果為r′，r′-m或r′-2m。因此，總的計算時間最多是5個周期，則

3 基于Stratix II器件的硬件實現

Stratix II器件是Altera在2004年初推出的采用1.2 V、90 nm、9層金屬走線、全銅SRAM工藝制造的高端FPGA［6］，它的內部主要特性有內嵌RAM模塊、DSP塊、鎖相環（PLL）和外部的存儲器接口等，同時采用了全新的邏輯結構——自適應邏輯模塊（Adaptive Logic Module，ALM），在降低了成本的基礎上顯著地提高了性能和邏輯利用率。

文中基于StratixII系列器件EP2S180F1508C3芯片，以Quartus II 9.0為開發環境，采用硬件描述語言VHDL進行進位保留Barrett模乘法器的FPGA設計與實現，并對實現結果分析驗證。

4 進位保留Barrett模乘法器的設計

進位保留Barrett模乘法器，即乘法部分使用進位保留乘法器，求模運算部分使用 Barrett約減運算。電路如圖 3所示。

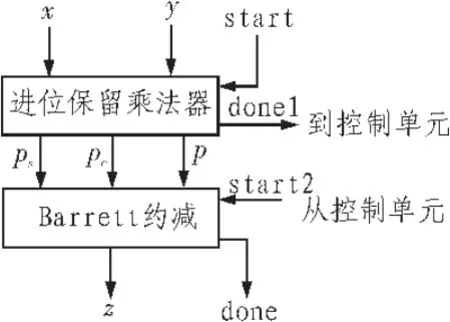
圖3 Barrett模乘法器Fig.3 Carry-save Barrett modular multiplication

如圖3中的第一個模塊是進位保留乘法器，第二個模塊是2節中的Barrett模約減電路，總的計算時間是計算兩個模塊所用時間的總和。

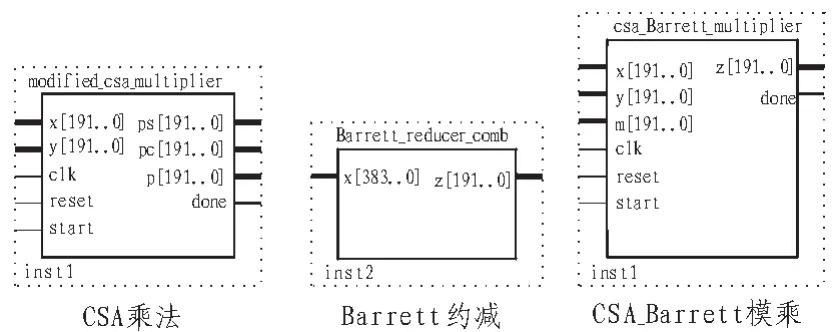
圖4 進位保留Barrett模乘法器接口定義Fig.4 Carry-save Barrett modular multiplication's block symbol files

圖3的接口定義如圖4所示。實現結果基于模齒為p192。

本文取模數：

m=p192=2192-264-1=（FFFFFFFFFFFFFFFFFFFFFFFFFFFF FFFEFFFFFFFFFFFFFFFF）16。仿真結果得出：共使用7 132個組合ALUTs，589個專用邏輯寄存器，仿真結果如圖5所示。

圖5 Barrett模乘法器仿真結果Fig.5 Carry-save Barrett modular multiplication’s simulation results

編譯和仿真后得到Barrett模乘法器的運行最高頻率為260.76 MHz，運行的總時鐘數為186，數據寬度為192 bit。根據公式：速度=最高頻率 （主頻）*數據寬度/運行總時鐘數（bit/s），經過計算得出運行速度：

260.76 MHz/186*192bit=269.17 Mb/s

表1為與已設計出的模乘法器的性能比較。

表1 性能比較Tab.1 Performance comparison

經過對比，可以看出本文設計出的模乘法器各方面綜合性能較佳。

圖 3中，x=（13579BDF）16，y=（2468ACE）16，計算出 z= （2C03A9277FA372）16，與仿真結果一致，則結果正確。改變模數m及被求模的數x，仍可驗證仿真結果的正確性。

5 結束語

本文應用 VHDL語言，利用進位保留乘法器及Barrett約減運算，設計出Barrett模乘法器，并在QuartusⅡ9.0環境下進行了綜合仿真驗證，結果與理論一致，驗證其正確性。這種方法能夠充分發揮硬件的速度和并行性，計算速率可以達到269.17 Mb/s，相比于Barrett算法［8］中的預計算部分使用的除法算法，在Barrett模乘法器只用到乘法算法及模約減運算，大大降低了設計復雜度以及硬件成本，運算效率提高，在公鑰密碼體制領域應用前景廣闊。

［1］張遠洋.素數域上公鑰密碼加速器庫的研究與實現［D］.鄭州：解放軍信息工程大學，2007.

［2］Jean-Pierre Deschamps，José Luis Ima？a，Gustavo D.Sutter，et al.Hardware Implementation of Finite-Field Arithmetic ［M］.3rd ed.［S.l.］:The McGraw-Hill Companies，2009.

［3］Parhami B.Computer Arithmetic［M］.New York:Oxford University Press，2000.

［4］Ercegovac M D，Lang T.Digital Arithmetic［M］.San Francisco: Morgan Kaufmann，2004.

［5］J.-P.Deschamps，G.Bioul，G.Sutter，et al.Synthesis of Arithmetic Circuits［M］.Wiley，Hoboken，New Jersey:Wiley，Hoboken，2006.

［6］葛亞明，彭永豐，薛冰，等.零基礎學FPGA［M］.北京：機械工業出版社，2010.

［7］TENCA A F，TODOROV GKOC C K.High-radix Design of a Scalable Modular Multiplier［A］.Cryptography Hardware and Embedded System-CHES 2001.Springer Verlag，Berlin，Gcrmanv，2001：189-205.

［8］Barrett P.Implementing the Rivest，Shamir and Adleman Public-key Encryption Algorithm on Standard Digital Signal Processor［C］.In:Cryptology-CRYPTO’86 Proceedings，vol.263 of Lecture Notes in Computer Science，Springer-Verlag，1987:311-323.

FPGA design and implementation of the carry-save Barrett modular multiplication

CHE Wen-jie，GAO Xian-wei
（Beijing Electronic Science and Technology Institute，Beijing 100070，China）

modulo arithmetic operation of multiplication on prime field is the most basic and most time-consuming operation，therefore，It is very important to design the faster operation speed，less resource efficient multiplier，This paper design a carry-save Barrett modular multiplier，multiplication part use carry-save multiplier，the modulo operation part use Barrett subtraction operation，It's designed and implemented on FPGA by hardware description language and the implementation results are verified.The Barrett modular multiplication operation requires approximately 186 clock cycles and the calculated rate can reach 269.17Mb/s for 192 bit operand.

Barrett modulo subtraction algorithm；Barrett modular multiplication；Field Programmable Gate Array；hardware description language

TN918.2

A

1674－6236（2016）04-0007-03

2015-03-03 稿件編號：201503048

北京市教育教學改革項目（121）；北京電子科技學院教研基金項目（jy201218）

車文潔（1991—），女，甘肅天水人，碩士研究生。研究方向：密碼算法的硬件實現等。