模糊控制在換熱器溫度控制系統(tǒng)中的應(yīng)用

強明輝，韓春春，王 宇

（蘭州理工大學 電氣工程與信息工程學院，甘肅 蘭州 730050）

模糊控制在換熱器溫度控制系統(tǒng)中的應(yīng)用

強明輝，韓春春，王 宇

（蘭州理工大學 電氣工程與信息工程學院，甘肅 蘭州 730050）

溫度影響工業(yè)生產(chǎn)的產(chǎn)品質(zhì)量和效率，所以對溫度的控制尤為重要。文章主要針對汽-水加熱換熱器被加熱介質(zhì)的出口溫度設(shè)計控制系統(tǒng)。通過分析加熱器的特性和工作機理，建立動態(tài)數(shù)學模型，進行控制分析。將模糊控制技術(shù)應(yīng)用于換熱器的出口溫度控制系統(tǒng)中，結(jié)合MATLAB/Simulink仿真，并與傳統(tǒng)的PID控制相比較，說明模糊控制在換熱器的溫度控制中能獲得良好的動態(tài)和穩(wěn)態(tài)性能，可在工程應(yīng)用領(lǐng)域得到推廣。

換熱器；數(shù)學模型；模糊控制；仿真

換熱器是使熱量從熱流體傳遞給冷流體的節(jié)能設(shè)備，又稱熱交換器［1］，在化工、石油、電子等工業(yè)部門應(yīng)用廣泛。因此換熱器的正確使用、過程控制及性能改善都對能源的有效利用及開發(fā)有著十分重要的意義。

換熱器的過程控制包括對溫度、流量等的控制，因為溫度直接影響產(chǎn)品質(zhì)量和效率，因此主要研究溫度控制。而且換熱器的動態(tài)特性復(fù)雜，傳統(tǒng)的PID控制很難滿足動、穩(wěn)態(tài)的性能要求，文章主要研究模糊控制在換熱器溫度控制中的應(yīng)用［2］。

1 換熱器的數(shù)學描述

換熱器的開發(fā)研制、實驗研究及過程控制都以產(chǎn)品的性能測試為前提。性能測試建立在熱平衡［3-4］的基礎(chǔ)上，即熱流體放出的熱量與冷流體獲得的熱量基本相等或相對誤差在一定范圍內(nèi)的情況下，實時測量與換熱器性能有關(guān)的現(xiàn)場數(shù)據(jù)，如溫度、流量及壓力等，傳送到PLC和上位機，進行控制反饋、數(shù)據(jù)的顯示及處理等。

假設(shè)忽略換熱過程的熱損失，則有：

1）熱平衡方程：

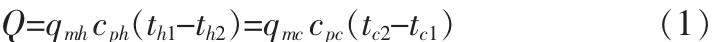
2）傳熱基本方程：

3）對數(shù)平均溫差：

4）熱平衡相對誤差：

式中：Q—熱負荷，W；K—總傳熱系數(shù)，W/（m2·K）；A—傳熱面積，m2；Δtm—對數(shù)平均溫差，℃；qmc、qmh—冷、熱流體的質(zhì)量流量，kg/s；cpc、cph—冷、熱流體的定壓比熱容，J/（kg·K）；tc1、tc2—冷流體進、出口溫度，℃；th1、th2—熱流體進、出口溫度，℃。

ΔQ＜5%，K當，的測試誤差小于10%時，認為系統(tǒng)達到平衡狀態(tài)，可進行性能測試。

2 換熱系統(tǒng)的數(shù)學模型

換熱器中以蒸汽加熱器應(yīng)用最多，浪費也最多。文中主要研究汽—水加熱器的溫度控制，取蒸汽流量作為控制量，將被加熱介質(zhì)的出口溫度作為被控量組成控制系統(tǒng)［2，4］。

2.1 被控對象的特性

加熱器中被加熱介質(zhì)沿管子流動方向的各點溫度分布不同，所以具有分布參數(shù)；這種對象即使在平衡狀態(tài)時，對象內(nèi)部的參數(shù)分布也不均勻，且傳熱時存在熱阻（對流熱阻與傳導(dǎo)熱阻），應(yīng)看作由多個容積和阻力組成，因此又是多容對象。總體來說是具有分布參數(shù)的多容對象［4］。在描述動態(tài)特性時，可以近似看作由3個集中容積的串聯(lián)組成，即三容過程，因此系統(tǒng)在反映輸入和擾動作用時存在較大延時。機理分析和工程實踐都表明，換熱器是一種慣性和時間滯后均較大，且很難用解析法建立數(shù)學模型的非線性復(fù)雜系統(tǒng)。

2.2 換熱器的數(shù)學模型的建立

1）數(shù)學模型的低階近似

從嚴格的傳熱理論分析，換熱器的傳熱過程要采用偏微分方程來描述。但換熱器動態(tài)特性復(fù)雜，用偏微分方程求解復(fù)雜，且所得模型階次高，難于用于實際計算和控制。文章采用低階近似的方法處理復(fù)雜的高階模型［4］，將換熱器這個三容時滯對象用一階滯后環(huán)節(jié)近似描述為：

式中，K—放大系數(shù)；T—時間常數(shù)；τ—滯后時間。它是由將多容對象處理為單容對象時引入的容量滯后時間τc和由工藝介質(zhì)傳輸距離引起的純滯后時間τ0兩部分組成的［4］。

2）參數(shù)的確定

通過階躍響應(yīng)法建立數(shù)學模型。實驗時，采用時間域法，在換熱器的輸入端人為輸入一個階躍擾動，測定設(shè)備輸出的階躍響應(yīng)曲線，根據(jù)響應(yīng)曲線計算對象的特性參數(shù)。

K、T、τ參數(shù)的求解步驟如下［4］：

①對換熱器系統(tǒng)做階躍響應(yīng)測試，得出一組數(shù)據(jù)；

②根據(jù)①中數(shù)據(jù)作階躍響應(yīng)曲線圖（見圖1）；

③在換熱器階躍響應(yīng)曲線圖中，找出系統(tǒng)輸出達到階躍給定的和的兩點對應(yīng)的時間t1和t2；

④由下式計算：

式中：R—階躍輸入幅值；Δy—系統(tǒng)輸出響應(yīng)，即：Δy= y（00）-y（0）

⑤由圖1得，t1=11.5，t2=19.8。

求得換熱器動態(tài)模型：

⑥對求得的G（s）作階躍響應(yīng)仿真，與圖1曲線比較，若曲線近似，則取G（s）為換熱器數(shù)學模型。階躍響應(yīng)仿真曲線如圖2所示。

以上兩圖對比可見：曲線近似一致，說明可對建立的數(shù)學模型進一步研究。

3 模糊控制在換熱器溫度控制中的應(yīng)用

模糊控制是以模糊集合論、模糊語言變量及模糊邏輯推理為基礎(chǔ)的一種計算機數(shù)字控制方法，以模糊數(shù)學為基礎(chǔ)，核心部分為模糊控制器。

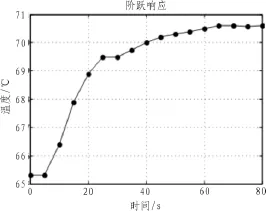
圖1 換熱器階躍響應(yīng)曲線圖Fig.1 Heat exchanger step response curve

圖2 階躍響應(yīng)仿真曲線Fig.2 The step response simulation curve

3.1 模糊控制的原理

模糊控制系統(tǒng)的組成類似于一般的數(shù)字控制系統(tǒng)，基本原理見圖3，模糊控制器原理見圖4。

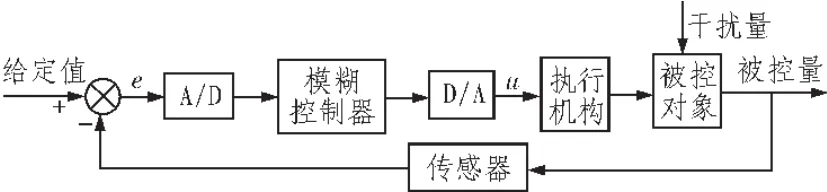
圖3 模糊控制系統(tǒng)原理框圖Fig.3 The principle diagram of fuzzy control system

3.2 模糊控制器的設(shè)計

選取誤差和誤差變化率作為模糊控制器的輸入變量，并選取控制量的變化作為模糊控制器的輸出變量。

1）模糊化、清晰化及變換因子

設(shè)［-xe，xe］、［-xec，xec］和［-yu，yu］分別為 e、ec和 u的基本論域，它們都是精確量。把覆蓋模糊語言變量的所有模糊子集的論域稱為模糊論域。

將輸入精確值從基本論域變換到模糊論域的系數(shù)，稱為量化因子。將精確量轉(zhuǎn)化為模糊量的過程稱為模糊化［5-6］。

將模糊推理得到的控制量（模糊量）變換為論域范圍的清晰量的過程稱為清晰化。經(jīng)清晰化處理的輸出變量是表示在模糊論域內(nèi)的，需要變換為執(zhí)行機構(gòu)需求的實際控制量。將輸出從模糊論域變換到基本論域的系數(shù)，稱為比例因子［5-6］。

本系統(tǒng)中，對溫度誤差E、誤差變化率EC和控制量U的模糊子集及模糊論域定義如下：

E的模糊集：

｛NB，NM，NS，NO，PO，PS，PM，PB｝

EC和U的模糊集：

｛NB，NM，NS，ZO，PS，PM，PB｝

E的模糊子集區(qū)分NO和PO，是為了提高穩(wěn)態(tài)精度。

模糊子集的隸屬度函數(shù)分別為：NB取Z形隸屬函數(shù)，PB 取S形隸屬函數(shù)，其余模糊子集均取三角形隸屬度函數(shù)。

2）參數(shù)確定

ke、kec及ku對控制系統(tǒng)的動態(tài)性能影響很大［4-6］。ke越大，系統(tǒng)調(diào)節(jié)惰性越小，上升速率越快，但過大會增大超調(diào)；kec越大，對系統(tǒng)狀態(tài)變化的抑制能力增大，增加了系統(tǒng)的穩(wěn)定性，但過大會使過渡時間變長；ku增大，系統(tǒng)響應(yīng)速度加快，但過大會導(dǎo)致超調(diào)增大乃至發(fā)生振蕩。

綜合考慮系統(tǒng)的動態(tài)和穩(wěn)態(tài)性能，取E和EC的論域為［-3，3］，U的論域為［1，7］，量化因子ke=3，kec=15，比例因子ku= 0.25。

4 仿真比較

利用MATLAB的Fuzzy Logic Toolbox根據(jù)上述步驟建立模糊推理系統(tǒng)（FIS），并將其嵌入Simulink仿真模型的模糊控制器模塊，實現(xiàn)與Simulink的連接并進行仿真。對比常規(guī)PID控制仿真結(jié)果，說明各自的優(yōu)缺點。仿真結(jié)果見圖5。

由Ziegler-Nichols整定法結(jié)合手動調(diào)節(jié)確定PID控制器3個參數(shù)的取值為：

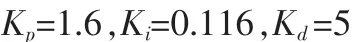
由上圖可見：PID控制響應(yīng)速度快，但超調(diào)量大，震蕩周期多，穩(wěn)定時間長；模糊控制無超調(diào)、調(diào)節(jié)時間短、穩(wěn)態(tài)性能好，控制效果優(yōu)于PID控制，可獲得較好的動態(tài)和穩(wěn)態(tài)性能。

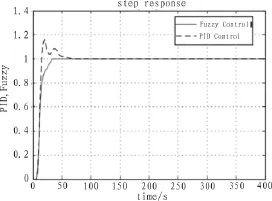
圖5 仿真結(jié)果Fig.5 Simulation result

5 結(jié) 論

文中通過分析換熱器工作機理，建立數(shù)學模型，將模糊控制和PID控制分別用于換熱器的出口溫度控制，經(jīng)MATLAB/Simulink仿真，說明模糊控制在抑制超調(diào)、減少調(diào)節(jié)時間等方面的優(yōu)點，尤其在處理過程復(fù)雜、具有非線性特點的被控對象時可以體現(xiàn)其優(yōu)越性。并且，F(xiàn)uzzy Logic Toolbox提供的5個圖形用戶界面（GUI）可視化程度高，容易實現(xiàn)FIS的編輯和調(diào)試。因此，可利用模糊控制算法實現(xiàn)換熱器的溫度控制。

［1］史美中，王中錚.熱交換器原理與設(shè)計［M］.4版.南京:東南大學出版社，2009.

［2］梅國梁，韓厚德.模糊控制技術(shù)在換熱器控制系統(tǒng)中的應(yīng)用［J］.機電設(shè)備，2009（1）:22-26.

［3］童正明，靳晶，秦桂花，等.1種板式換熱器測試平臺及應(yīng)用［J］.化工生產(chǎn)與技術(shù)，2012，19（3）:44-46.

［4］張亞萌.智能模糊控制技術(shù)在換熱器控制系統(tǒng)中的應(yīng)用［D］.天津:天津大學，2005.

［5］王麗娟.模糊控制在非線性系統(tǒng)中的研究［J］.電子設(shè)計工程，2012，20（4）:73-75.

［6］石辛民，郝整清.模糊控制及其MATLAB仿真［M］.北京：清華大學出版社，2008.

Application of fuzzy control in heat exchanger temperature control system

QIANG Ming-hui，HAN Chun-chun，WANG Yu
（School of Electrical Engineering and Information Engineering，Lanzhou University of Technology，Lanzhou 730050，China）

Temperature can influence the product quality and efficiency in industrial production，so temperature control is particularly important.Aiming at the outlet temperature of the heated medium in steam-water heaters，a control system is designed in the paper.By analyzing the characteristics and working mechanism of heaters，the dynamic mathematical model is set up and performance is analyzed.Fuzzy control technology is applied to the outlet temperature control system for heat exchanger，after modeling and simulation in MATLABSimulink，and by comparison with PID control，it has shown that fuzzy control in temperature control of heat exchangers can get good dynamic and steady-state performance，which can be promoted to engineering application.

heat exchanger；mathematical model；fuzzy control；simulation

TN01

A

1674－6236（2016）04-0072-03

2015-03-21 稿件編號：201503292

強明輝（1960—），男，陜西扶風人，教授級高級工程師。研究方向：過程控制，檢測技術(shù)。