旋轉矢量多迭代捷聯姿態解算誤差補償算法

王　真，高鳳岐，高　敏，高偉偉

（軍械工程學院，河北　石家莊　050003）

旋轉矢量多迭代捷聯姿態解算誤差補償算法

王真，高鳳岐，高敏，高偉偉

（軍械工程學院，河北石家莊050003）

為克服高動態條件下的捷聯姿態解算存在不可交換性誤差的問題，達到進一步增強捷聯姿態誤差抑制效果的目的，基于角速率的輸出提出了等效旋轉矢量三子樣二次迭代優化算法，推導對應的圓錐補償算法方程及其表達式。分別在不同圓錐運動頻率情況下和不同姿態更新頻率情況下，展開仿真驗證算法的漂移誤差和俯仰角誤差，以傳統的四元數法、三子樣算法為對照，分析仿真數據曲線，得出本改進算法在精度和穩定性方面均有較大提高。在單軸速率轉臺上進行光纖陀螺的實測驗證中，通過調整圓錐運動半偏角和頻率，測量獲取光纖陀螺慣組輸出情況，結果表明：該算法在高動態條件下受圓錐半角、圓錐運動頻率的影響較小，性能更加優越。

捷聯姿態測量；高動態；圓錐誤差補償；等效旋轉矢量

0　引言

捷聯慣性導航系統一般與載體固聯，直接感測載體的運動［1］，姿態實時計算是捷聯慣導的關鍵技術［2］。在導彈等高過載、高頻姿態變化的高動態環境下，傳感器采集的離散點信息較難反映真實的載體空間轉動次序，圓錐運動時尤為明顯，故也稱圓錐誤差。圓錐誤差是姿態解算的重難點問題，方向余弦法、四元數法［3］、三子樣算法［4］等傳統圓錐補償算法會引起較大的不可交換性誤差［5］。作為高動態情形下的誤差抑制重難點，圓錐誤差的有效抑制對導彈等載體的姿態解算準確度提高有顯著意義。

陳建鋒等［6］提出一種角速率輸入下的二次優化補償算法，湯傳業等［7］引入最小二乘方法進行圓錐誤差補償優化，Song等［8］進一步討論了傳統的圓錐誤差補償算法在機動條件下的實用性問題，黃磊等［9］提出了基于高階補償模型的新圓錐算法。

本文針對高動態圓錐誤差補償的難題，以等效旋轉矢量三子樣算法為基礎，基于增加旋轉矢量迭代次數提出了一種基于角速率輸出的二次迭代改進算法，并優化了旋轉矢量計算系數。通過上述算法改進，減小姿態更新過程中的計算量，有利于提高姿態解算準確度，尤其是在高動態條件下提高算法性能。

1　改進型算法的提出

基于陀螺角增量輸出是傳統的等效旋轉矢量法的研究前提，這種方法需要先轉換角增量信息為角速率信息，再計算等效旋轉矢量，這無疑增加了算法計算量且引入誤差。直接針對基于角速率輸出的算法研究并不多，本文旨在破除轉換環節，直接面向角速率輸出，從而提升算法性能和解算準確度。

1.1角速率輸出的等效旋轉矢量推導

下面推導針對角速率輸出的等效旋轉矢量，其過程如下：

記tk是第k次采樣時刻，設h為姿態更新的周期，且h=tk-tk-1，在姿態更新周期內，記等效旋轉矢量為Φ（h），在h=0處用泰勒級數法將Φ（h）展開：

Φ（0）顯然為0。ω是載體系相對于參考系的轉動角速率，運用三次型拋物線對其進行擬合，過程如下：

令在tk-1、tk-1+h/3、tk-1+2h/3、tk時刻計算出的角速率分別對應為ω1、ω2、ω3、ω4，將其代入上面的公式，得到四元數q（h）：

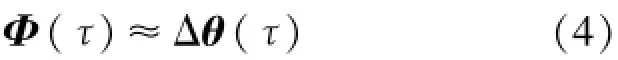
由此可推得ω（tk-1+），Δθ（）在=0處及各階導數為

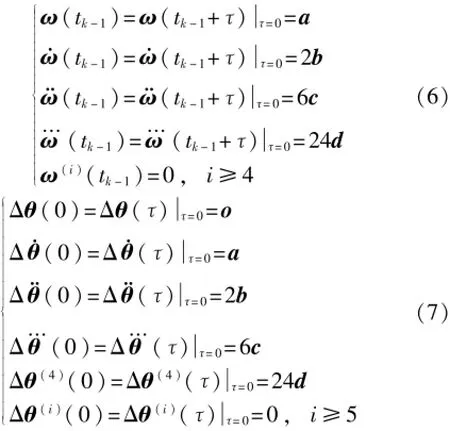
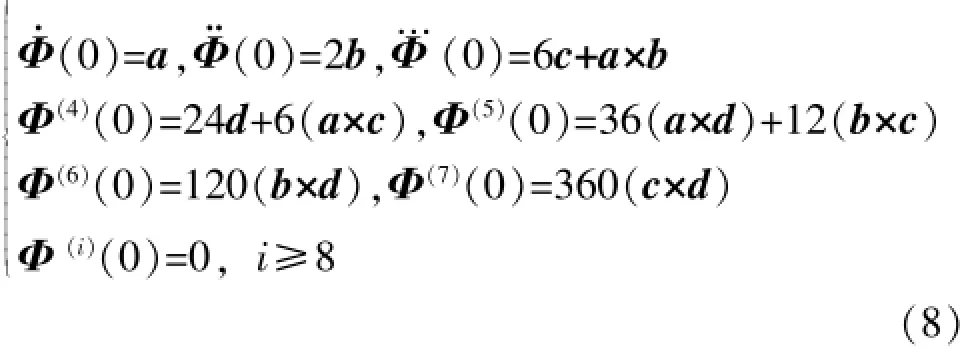
將上式代入Φ（h）在h=0處的泰勒展開式，由角速率系數與角速率的關系，得到基于角速率輸出的等效旋轉矢量估計值為

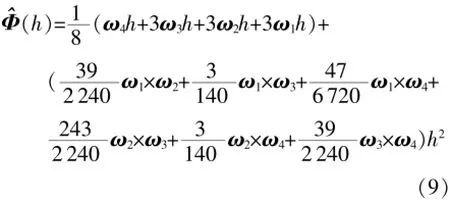
上式是對角速率進行三次曲線擬合后得到的，于是稱其為基于角速率輸出的等效旋轉矢量三子樣算法。得到等效旋轉矢量Φ后，可計算出姿態更新周期內的變化四元數q（h），表示如下：

在下個姿態更新周期的初始時刻，其四元數Q（t+h）可算出，并有如下表示（?為四元數乘）：

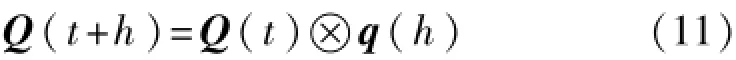
在姿態更新周期內，四元數更新由此實現。選取在平衡位置附近旋轉的圓錐運動，其等效旋轉矢量：

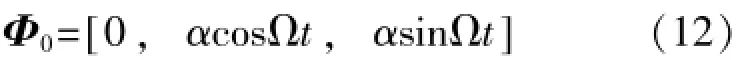
式中：α——圓錐角；

Ω——角頻率。

在上面描述的運動情況下，其四元數為

根據式（11），得到：

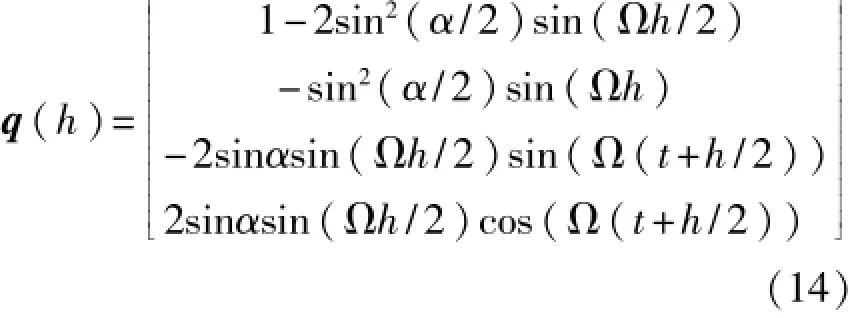
那么，相對應的角速率ω（t）可表示為

若姿態更新頻率較大時，sin（Φ/2）≈Φ/2，近似簡化后的等效旋轉矢量：

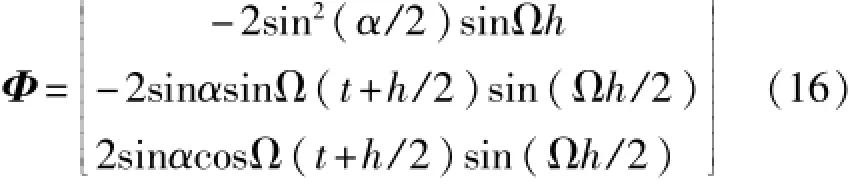
旋轉矢量誤差Φε=Φ-。若想讓Φε最小，需要設置低次冪項為零，從而得出在圓錐運動情況下，在沿著圓錐軸軸向的等效旋轉矢量的誤差估計值為

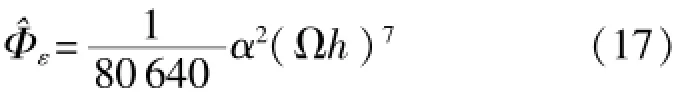
1.2等效旋轉矢量算法的改進

在姿態更新頻率較高的條件下，采用多次迭代辦法更新旋轉矢量，對抑制圓錐誤差有積極影響。按照這一思想，在基于角速率輸出情況，推導了等效旋轉矢量的三子樣二次迭代優化算法。

二次迭代更新時，設h為姿態更新周期，其迭代周期T=h/2，［tk-1，tk-1+T］和［tk-1+T，tk-1+2T］則分別為兩段迭代周期。在迭代周期［tk-1，tk-1+T］內，相對參考系下的載體系角速率可表示為［10］

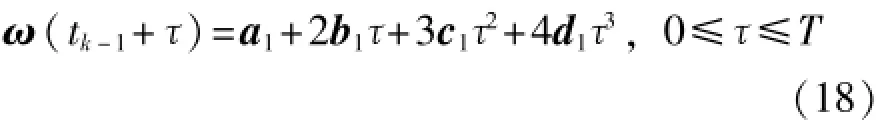
用泰勒級數展開Φ（tk-1+T）。

Φ（tk-1）=0，則Φ 在t=tk-1時刻各階導數皆可知，綜上可得：

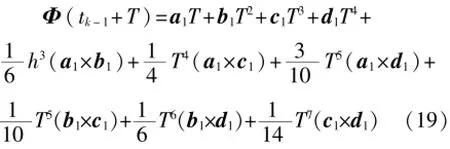
在［tk-1+T，tk-1+2T］周期內，其表達式亦同理可得。

綜合上面的內容，在姿態更新周期內，關于旋轉矢量的估計結果表示如下：

旋轉矢量增量為

Mij，Nij分別作為角速率叉乘項的待定系數。

對系數優化過程如下：

在典型的圓錐情況時，ωi×ωj僅僅與相對時間間隔h（j-i）有關聯。故將上式簡化為

在典型圓錐運動條件下，算法的誤差漂移［11］：

用泰勒公式將上式展開，可以獲到Ωh的各階系數，令（Ωh）3，（Ωh）5，（Ωh）7的系數為零。算法可表示為如下形式：

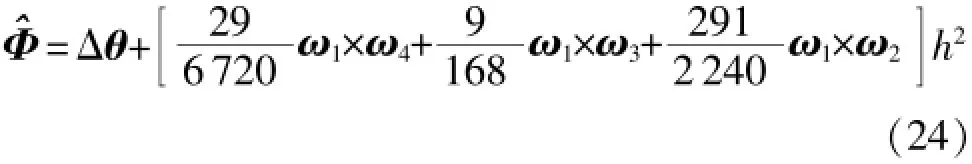
其中

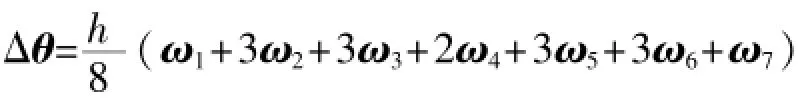
表示姿態更新周期內角增量值［12］。

2　仿真實驗分析

開展仿真實驗的總體思路是將四元數法［13］、三子樣算法［14］還有改進算法進行對比，來驗證本文改進算法的效果，實驗過程中預設圓錐角α=1.5°。

2.1驗證算法漂移誤差

首先，將圓錐運動的頻率固定為4Hz，隨著姿態更新頻率的變化，觀察算法漂移誤差（X軸方向分量），如圖1所示。然后，將姿態更新頻率固定為100Hz，隨著圓錐頻率的變化，觀察算法漂移誤差（X軸方向分量）變化情況，如圖2所示。

圖1　不同姿態更新頻率下的算法誤差

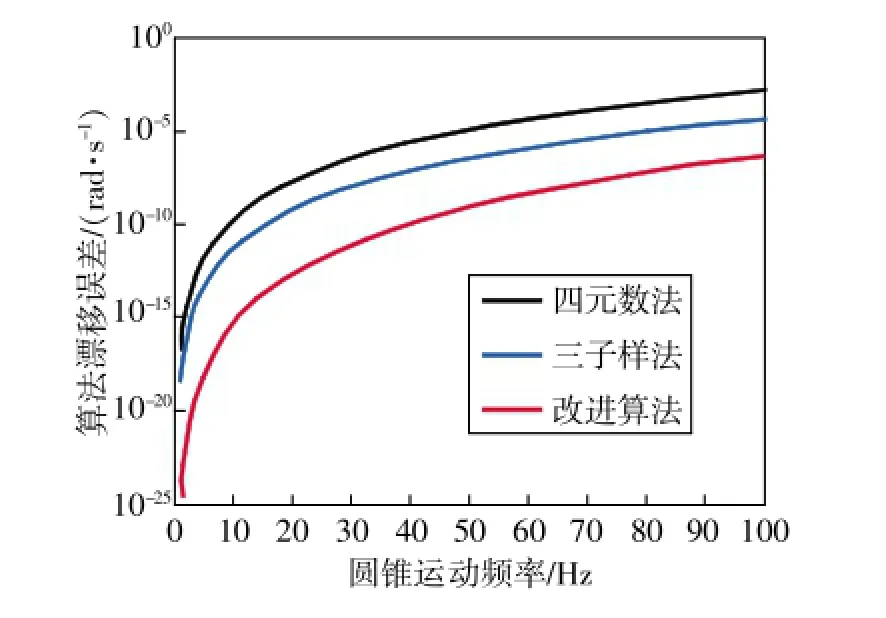
圖2　不同圓錐運動頻率下的算法誤差

由圖知，算法漂移誤差與圓錐運動頻率呈正比，與姿態更新頻率呈反比，改進算法在抑制圓錐運動誤差方面性能更佳。

2.2驗證俯仰角誤差

以俯仰角解算為例［15］，以期望更加直觀地分析圓錐運動施加于姿態解算的影響。在較典型圓錐運動條件［16］下，分別采用3種算法計算相對參考系的載體俯仰角。

設α=1.5°，仿真時間t=300s，分別在錐頻率4Hz、8 Hz條件下，采用以上算法得到的俯仰角誤差結果如圖3和圖4所示。

2.3分析仿真結果

在設定好的圓錐運動情況下，四元數法解算出的俯仰角誤差相較之下明顯較大；當圓錐頻率比較低時，關于俯仰角解算誤差，改進算法優于三子樣算法但在精度與穩定性方面相差不是很大，但當圓錐頻率明顯增大時，改進算法在精度與穩定性方面的優勢更加顯著。

3　圓錐誤差補償實測數據驗證

3.1試驗平臺及試驗條件

為更好地驗證本改進型補償算法在圓錐運動條件下的性能，搭建實測試驗平臺，其主要組成是被測光纖陀螺和單軸速率轉臺。

在單軸速率轉臺上，運用某型光纖陀螺慣組來模擬載體的圓錐運動。用安裝偏角模擬半錐角α，圓錐運動頻率f由設定速率轉臺參數來模擬，姿態更新周期h是在姿態解算算法中設定的。具體實驗條件如表1所示。

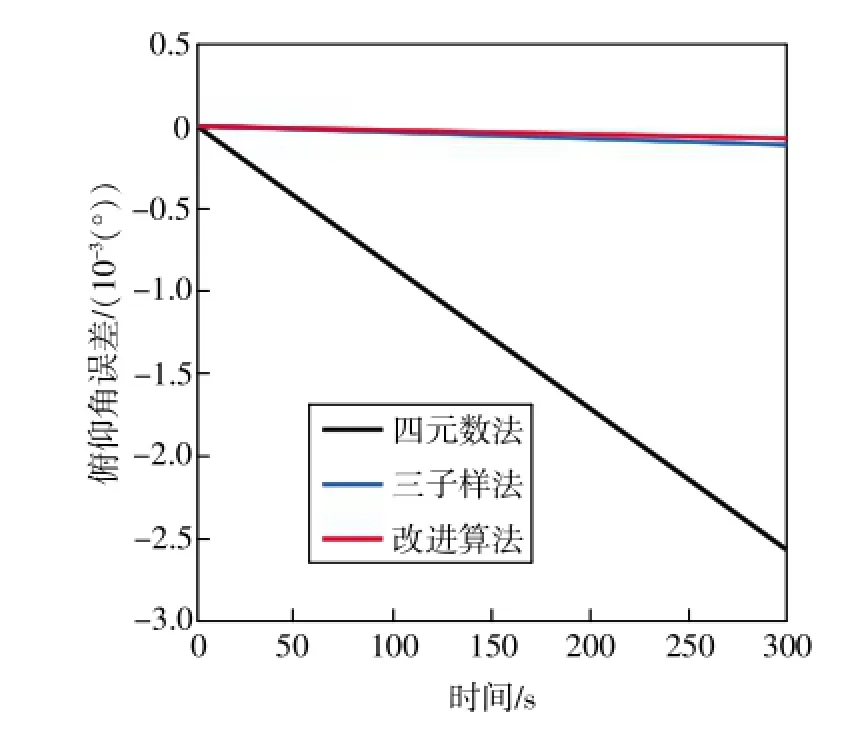
圖3　錐頻率4Hz下的俯仰角誤差

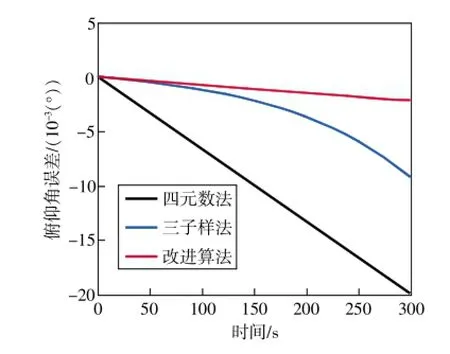
圖4　錐頻率8Hz下的俯仰角誤差

表1　實測的實驗條件

3.2實測數據情況

實測試驗開展的思路是，調整圓錐運動情況，獲取光纖陀螺慣組輸出情況，圓錐運動的調整分別由不同α、f來實現。需要指出的是，在實驗中沒必要對半錐角詳細羅列，僅區分較小與較大兩大類情況即可，并且分別由as和am表示。

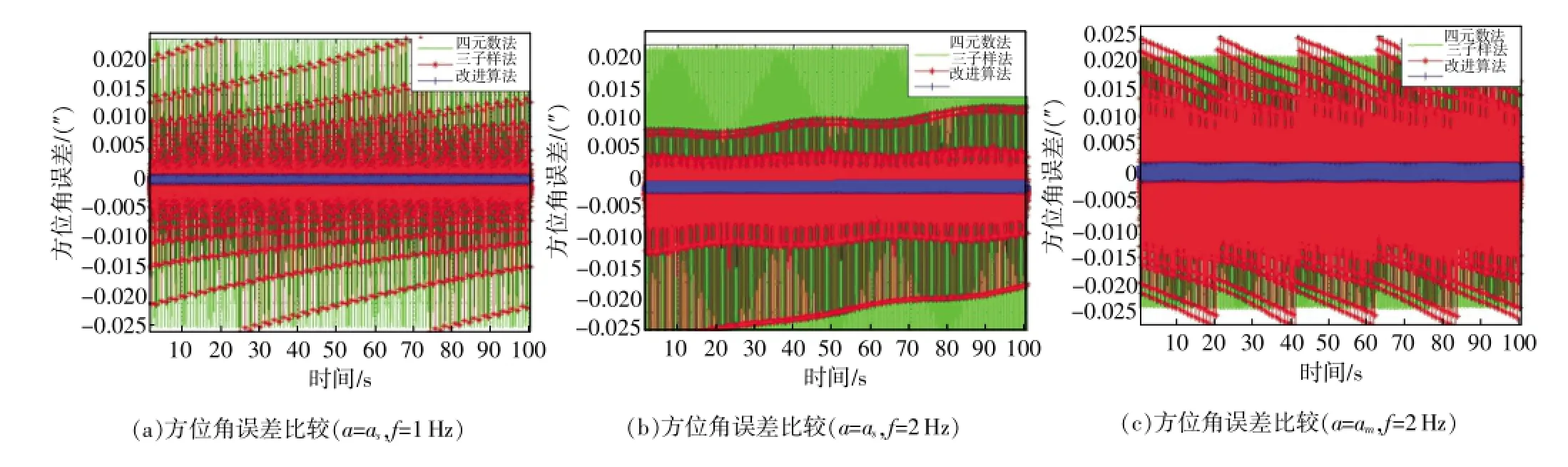
圖5　不同模擬圓錐運動下方位角誤差

實測3組數據，兩兩互為對比，具體條件設定如表2所示。

表2　實測的條件設定情況1）

在單軸速率轉臺上固定慣組后，通過初始精對準得出兩個半錐角數值：as=0.9527°，am=3.9318°。以方位角為例，對比3種算法在3組條件下的姿態解算誤差情況，結果如圖5所示。

3.3實測結果分析

在同一種圓錐運動情況下對比，本改進算法的姿態解算精度比其他兩種算法大幅提升，幾乎提升了一個數量級。在圓錐半角一樣時，圓錐運動頻率越大則引起更大的姿態解算誤差；在圓錐頻率一樣時，圓錐半角越大則引起更大的姿態解算誤差。本改進型算法相比前兩種算法來說，受圓錐半角、圓錐運動頻率的影響很小，算法性能更加穩定。

4　結束語

為有針對性地解決高動態條件下傳統圓錐補償算法有不可交換性誤差的問題，探討了基于角速率輸出的等效旋轉矢量的三子樣二次迭代優化算法，推導了相關的圓錐補償算法方程及表達式。

通過仿真計算和試驗驗證，對比四元數法和三子樣法，證明了本改進算法的優越性。首先，在不同的圓錐頻率與不同更新頻率情況下，本改進算法的誤差精度方面均有較明顯提高；其次，本改進算法受圓錐半角、圓錐頻率帶來的影響更小，高動態下性能更優與穩定性更好。此外，本算法的研究能針對性地解決高動態姿態解算的不可交換性誤差補償的問題，解決了算法復雜度與計算實時性的矛盾，改善整體性能，為下一步繼續深入挖掘圓錐誤差補償算法提供有益的理論參考和實驗依據。

［1］程承，潘泉，李漢舟.一種新的捷聯慣導系統圓錐誤差補償算法研究［J］.彈箭與制導學報，2014，34（1）：1-4.

［2］李海濤，曹詠弘，祖靜.等效旋轉矢量法在旋轉彈姿態解算中的應用［J］.測試技術學報，2011，25（4）：287-291.

［3］張榮輝，賈宏光.基于四元數法的捷聯式慣性導航系統的姿態解算［J］.光學精密工程，2008，16（10）：1963-1970.

［4］MILLER R B.A new strapdown attitude algorithm［J］.Journal of Guidance Control and Dynamics，1983，6（4）：287-291.

［5］黃磊，劉建業，曾慶化.基于高階補償模型的新圓錐算法［J］.中國慣性技術學報，2013，21（1）：37-41.

［6］陳建鋒，陳熙源，祝雪芬.硬件增強角速率圓錐優化算法的姿態解算精度分析及改進［J］.東南大學學報（自然科學版），2012，42（4）：632-636.

［7］湯傳業，陳熙源，李建利.一種角速率輸入的圓錐算法設計［J］.中國慣性技術學報，2013，21（4）：456-461.

［8］SONG M，WU W Q，PAN X F.Approach to recovering maneuveraccuracyinclassicalconingalgorithms［J］. Journal of Guidance Control and Dynamics，2013，36（6）：1872-1880.

［9］黃磊，劉建業，曾慶化.基于高階補償模型的新圓錐算法［J］.中國慣性技術學報，2013，21（1）：37-41.

［10］屈熠，趙忠.增強型等效旋轉矢量算法在圓錐運動下的仿真［J］.計算機仿真，2010，27（11）：25-27.

［11］李海濤，曹詠弘，祖靜.等效旋轉矢量法在旋轉彈姿態解算中的應用［J］.測試技術學報，2011，25（4）：287-291.

［12］袁張賢，王鑫偉.斜直圓筒內基于Euler-Rodrigues參數的細長桿螺旋屈曲研究［J］.計算物理，2012，29（4）：549-556.

［13］梁鋒，周衛東，馬薈.基于四元數的艦船捷聯慣導粗對準方法研究［J］.艦船科學技術，2013，35（8）：53-56.

［14］湯傳業，陳熙源.一種角速率輸入的捷聯慣導姿態算法［J］.東南大學學報，2014，44（3）：543-549.

［15］彭孝東，張鐵民，李繼宇，等.基于傳感器校正與融合的農用小型無人機姿態估計算法［J］.自動化學報，2015，41（4）：854-860.

［16］HUANGL，LIU J Y，ZENG Q H.Optimized strapdown coning correctionalgorithm［J］.Transactions of Nanjing University of Aeronautics&Astronautics，2013，30（4）：343-349.

（編輯：李妮）

Research on error compensation improved algorithm of strapdown attitude&heading measurement based on multiple iteration rotation vector

WANG Zhen，GAO Fengqi，GAO Min，GAO Weiwei
（Ordnance Engineering College，Shijiazhuang 050003，China）

To reduce the traditional coning error compensation algorithm noncommutativity errors under high dynamic conditions and to restrain the coning error，proposed the three-sample-andtwo-time iteration algorithm of equivalent rotation vector based on angular rate，and deduced the expression of coning error compensation algorithm.At different coning motion frequency and update frequency，simulation validation showed this algorithm had advantages in accuracy and stability than quaternion and three sub-sample algorithms.Experimental results show that there was smaller influence of coning motion frequency and cone angle on this algorithm，thus this algorithm is better than traditional algorithm under high dynamic conditions.

strapdown attitude&heading measurement；high dynamic；coning error compensation；equivalent rotation vector

A

1674-5124（2016）08-0113-05

10.11857/j.issn.1674-5124.2016.08.023

2015-09-10；

2015-10-11

裝備預研共用技術基金項目（9140A05040213JB34069）

王真（1991-），男，河北唐山市人，碩士研究生，專業方向為精密儀器與微系統。