運用方格，調正相異構想
——“平行四邊形面積”教學實踐與思考

浙江余姚市實驗學校（315400） 毛亞峰

運用方格，調正相異構想
——“平行四邊形面積”教學實踐與思考

浙江余姚市實驗學校（315400） 毛亞峰

學生相異構想的產生直接影響學習的成效。因此，課堂教學中，教師需要正確把握相異構想的評估與調正策略的實施，引導學生調正相異構想，使之與科學概念相一致，從而打造高效的數學課堂。

相異構想評估調正平行四邊形面積前測反思

一、相異構想的前測

1.前測說明

我們在2014學年和2015學年分別就同一內容做了同一的前測，前測題如下：你能想辦法求出這個平行四邊形的面積嗎？可以應用下列材料。

材料：平行四邊形紙片（紙片上沒有數據，相鄰兩條邊的長為8厘米、5厘米，且8厘米底邊上的高是3厘米）、剪刀、細繩、三角板、1平方厘米的正方形紙片、鉛筆。

兩次前測的區別：2015學年的前測材料中提供了透明的網格。

2.前測結果統計

2014學年前測對象為城鎮學生1086名，農村學生917名，共計2003名學生。

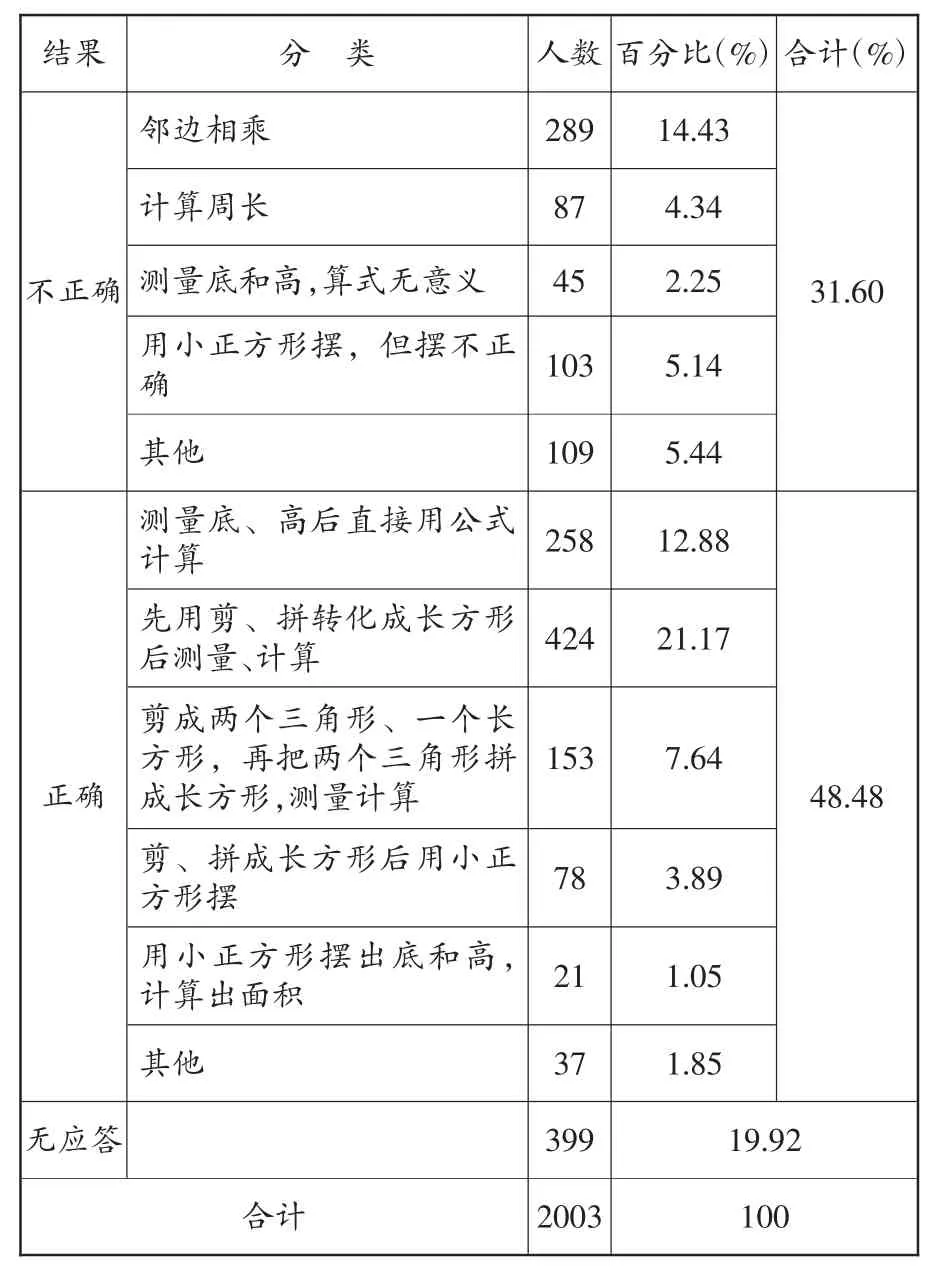
結果　分　類　人數百分比（%）合計（%）鄰邊相乘　289　14.43不正確31.60 103　5.14計算周長　87　4.34測量底和高，算式無意義　45　2.25用小正方形擺，但擺不正確其他　109　5.44測量底、高后直接用公式258　12.88計算先用剪、拼轉化成長方形424　21.17后測量、計算153　7.64正確48.48剪成兩個三角形、一個長方形，再把兩個三角形拼成長方形，測量計算剪、拼成長方形后用小正78　3.89方形擺用小正方形擺出底和高，21　1.05計算出面積其他　37　1.85無應答　399　19.92合計　2003　100

2015學年前測對象為城鎮學生1195名，農村學生832名，共計2027名學生。

結果　分　類　人數百分比（%）合計（%）鄰邊相乘　264　13.02不正確計算周長　54　2.66測量底和高，算式無意義　25　1.23用網格，但不會數　46　2.27 87　4.29其他　94　4.63 28.10用小正方形擺，但擺不正確　運用方格數方格：逐格拼組法　154　7.61 19.06 63　3.11測量底、高后直接用公202　9.97式計算先用剪、拼轉化成長方434　21.41形后測量、計算正確數方格：整體拼組法　169　8.34補成一個大長方形，放在網格上減去補的部分不運用方格剪成兩個三角形、一個長方形，再把兩個三角形拼成長方形，測量計算46.57 176　8.68剪、拼成長方形后用小99　4.88正方形擺用小正方形擺出底和16　0.79高，計算出面積其他　17　0.84無應答　127　6.27合計　2027　100

二、相異構想的評估

對學生相異構想的評估，主要從“四基”進行。如下：

1.確定評估標準

（1）基礎知識：探索并掌握平行四邊形面積計算公式的推導過程和計算方法。

（2）基本技能：能應用公式正確計算平行四邊形的面積，解決簡單的實際問題。

（3）基本思想：能用轉化的方法推導平行四邊形面積的計算公式，認識到轉化思想在平面圖形面積公式推導中的應用。

（4）基本活動經驗：在操作中積累轉化的活動經驗，以便在以后學習中遇到相似的問題時能調用該經驗加以解決。

2.評估相異構想

（1）負遷移影響明顯。

兩次前測均有較高比例的學生能正確得出平行四邊形的面積，有較好的學習基礎，但分別有14.43%和13.02%的學生用“鄰邊相乘”的方法計算，這是長方形面積計算方法負遷移的結果。

（2）方格仍是學生不可或缺的學習工具。

在第二次前測中，由于方格的引入，引發了學生更多的思考，使無應答的學生從19.92%下降到6.27%，提高了獨立探究的效率，這也說明學生積累了使用方格的活動經驗。

（3）缺乏轉化的活動經驗。

兩次前測顯示，把平行四邊形轉化成長方形進行測量、計算的約占21%。因此，教師在教學中需創設情境，引導學生調用已有的知識經驗，自發地把平行四邊形轉化成長方形進行研究。

三、調正策略的確定與實施

1.確定調正策略——借助方格引導探究

方格是學生熟悉的學習面積的工具，通常是指邊長為1厘米的小正方形，在幫助學生初步構建單位面積和推導長方形、正方形面積計算公式時，發揮了不可替代的作用。到了五年級學習“平行四邊形面積”時，教材中也編排了借助方格數平行四邊形面積的內容，但教師在課堂教學中出現了兩種處理方式：一是僅僅把方格當作數的工具，引導學生通過數平行四邊形和長方形的面積，發現兩者間的關系；二是完全拋棄了方格，認為五年級學生再用方格研究面積起點太低，直接進入了操作環節。我在教學實踐中充分發揮方格的不同功效，為調正學生的相異構想起到了積極的作用。

2.調正策略的實施

片斷（1）：簡要復習平行四邊形的特點，并出示前測結果。

出示右圖，讓學生計算出這個平行四邊形的面積，學生計算方法如下。

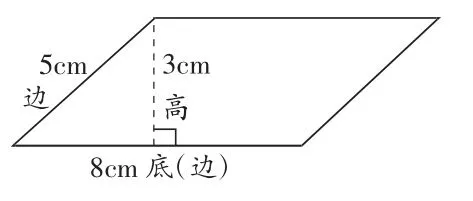
①（8+5）×2=26（cm2）求周長

②8×5=40（cm2）鄰邊相乘

③8×3=24（cm2）底乘高

片斷（2）：辨析鄰邊相乘。

師（指著第②種方法）：請你介紹自己的想法。

生1：因為長方形的面積是長乘寬，是鄰邊相乘，所以平行四邊形的面積也是鄰邊相乘，也就是8×5。

師：他從長方形的面積計算方法猜想到平行四邊形的面積是鄰邊相乘，有一定的道理。下面，我們來研究這種方法是不是正確的。你們想怎么研究？

生2：可以把平行四邊形放在網格上來研究。

師（引導并示范）：把平行四邊形的框架放在網格上推一推、看一看、想一想，你有什么發現？（學生操作，師巡視，然后交流）

生3：我發現不停地推下去，面積先是在變大，當推成長方形后面積達到最大，如果再推面積又開始慢慢變小。

生4：我發現這樣推，鄰邊的長度沒有變化，但是形狀變了，面積也變了。

師（小結）：我們把平行四邊形放在方格上，通過推來研究發現，用鄰邊相乘求平行四邊形的面積是——

生：錯誤的！

片斷（3）：研究底乘高。

師：底乘高是不是求平行四邊形面積的方法呢？你們準備怎么研究？

生5：剛才我們是在方格上研究的，那還是放在方格上研究吧！

師：平行四邊形的面積是底乘高嗎？你是怎么想的？

生6：我是數出來的。我先一格一格地數，正好有18格，這些不足一格的加起來共有6格，所以加起來是24格，也就是24平方厘米。這樣算，跟底乘高算出來的結果一樣。

師：像他這樣數，一共有24個1平方厘米，說明平行四邊形的面積就是24平方厘米，可以嗎？誰還有不同的方法？

生7：我不是數的，但我的方法比他簡便。我把平行四邊形的左邊三角形割下來，移到右邊，變成了長方形，8乘3是24，所以面積是24平方厘米。因此，我認為用底乘高這種方法求平行四邊形的面積是對的。

師：他用割補的方法，把平行四邊形轉化成長方形來研究，面積確實是24平方厘米。是不是所有的平行四邊形都能用割補的方法轉化成長方形呢？

生8：我認為可以。

生9：我有疑問，不太清楚。

師：到底可不可以呢？請你拿出平行四邊形的紙片試一試。

片斷（4）：拓展練習。

師：老師買了一個平行四邊形的車位，面積是18平方米，想一想，它可能會是怎樣的？把你想的畫在方格紙上。（學生想、畫，師巡視后展示學生畫的圖，如下）

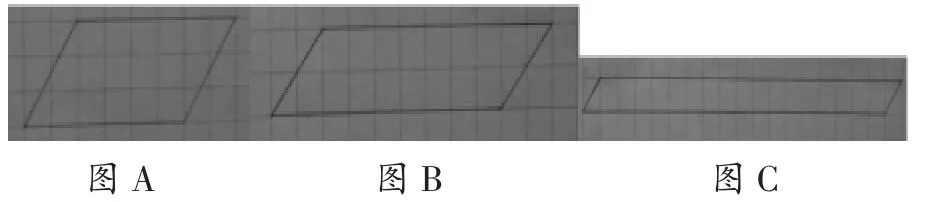
生10：我有不同意見。雖然它們的面積都是18平方米，但是圖B和圖C顯然不適合做車位，因為這樣的車位車是開不進去的。（其他學生紛紛點頭）

師：是啊，底9米、高2米和底18米、高1米的平行四邊形，雖然面積都是18平方米，但是卻不適合做車位，而第一種底6米、高3米的平行四邊形則比較合適做車位。底6米、高3米的平行四邊形還有兩種情況（如下圖），大家再來看一看，可以做車位嗎？

生：可以。

師：底6米、高3米的平行四邊形還有嗎？想一想，用手比劃一下。（在學生回答后）有多少個？

生：無數個。

師：是不是底6米、高3米的平行四邊形都合適呢？（出示下圖）比如這個平行四邊形，能做車位嗎？

生：不可以，車開不進去了。

師（小結）：我們在設計停車位的時候，不能光考慮它的面積，還要考慮它的形狀。

……

四、教學反思

小小的方格，在學生學習平行四邊形面積的不同環節中都發揮了極其重要的作用，是學生學習的“助推器”。其作用主要體現在以下幾個方面：

1.有助于激活、積累活動經驗

受知識、年齡的限制，小學生活動經驗的積累與更新必須在動手操作、用眼觀察、動口介紹、動腦思考中獲得。本課中有兩處由于恰當地使用了方格，有助于學生感性經驗的積累：一是在辨析鄰邊相乘是不是計算平行四邊形的面積計算方法時，這里的方格起著“量化”的作用；二是在數方格紙上平行四邊形的面積時，通過對比數的結果與底乘高計算的結果，初步肯定了底乘高是計算平行四邊形面積的方法。同時，在數的過程中（不足一格）不知不覺地用到了“補”的方法，為后續學習做好了方法上的準備。

2.有助于引發用割、補的方法轉化平行四邊形

平行四邊形面積計算公式的推導，是在用割、補的方法把平行四邊形轉化成長方形后，通過觀察兩者間的關聯進行的。那么，學生怎么就想到把平行四邊形轉化成長方形呢？在本課中，面對放在方格上的平行四邊形，不少學生都想到了把左邊的三角形割下來，“移”到另一邊，正好“補”成一個長方形。或許是這樣做便于數方格，或許是對長方形認識的思維定式影響，但學生的無心之舉，恰恰完成了本課的核心操作——用割、補的方法把平行四邊形轉化成長方形。接著，我通過提問，使學生迫不及待地進行探究，為成功驗證、推導平行四邊形的面積計算公式奠定了基礎。

3.有助于發展推理能力

五年級學生的思維正處于具體形象思維向抽象邏輯思維發展的過渡時期，因而在培養與發展推理能力時必須借助工具。如課中通過推放在方格上的平行四邊形框架，根據觀察所得推斷出鄰邊相乘不是求平行四邊形面積的方法；通過割、補方格上平行四邊形，推想是否所有的平行四邊形都能用這種方法轉化成長方形；通過觀察、比較畫在方格上的平行四邊形車位，結合生活經驗推測車位形狀的合理性……這里，小小的方格成為學生順利展開想像、發展推理能力不可或缺的輔助工具。

4.有助于學以致用

通過數學學習，使學生學會嘗試用數學眼光審視生活，用數學思維思考生活現象，用數學方法解決生活中的實際問題。如何在本課中落實這一潛在目標呢？我設計了“畫平行四邊形停車位”的拓展練習，使學生借助方格邊畫邊想，自主地把數學與生活緊密地聯系起來。

（責編藍天）

G623.5

A

1007-9068（2016）23-022