某鋼螺旋梯道的設計及計算方法研究

牛偉迪（同濟大學建筑設計研究院集團有限公司）

某鋼螺旋梯道的設計及計算方法研究

牛偉迪
（同濟大學建筑設計研究院集團有限公司）

本文針對某鋼螺旋梯道，采用空間梁單元結構模型和空間梁-板混合單元模型兩種方法，對該梯道進行建模計算。通過對兩種模型的計算結果分析比較發現：該螺旋梯道應力及位移滿足規范要求；空間梁單元結構模型建模過程簡單，便于應用，計算結果偏安全，適用于工程應用；空間梁-板混合單元結構模型建模較為復雜，能夠更好地考慮橫梁對整體結構的影響，計算結果相對精確。

鋼結構；螺旋梯道；空間梁單元結構模型；空間梁-板混合單元結構模型

1　前言

梯道的造型在一些對景觀要求較高的橋梁設計中，往往會起到錦上添花的作用。螺旋梯道以其優美飄逸的外形曲線，得到了業主和廣大設計人員的認可。某橋梁全長305m，位于某公園內，對景觀要求比較高，因此根據需求在主橋兩側對稱布置四座鋼螺旋梯道。

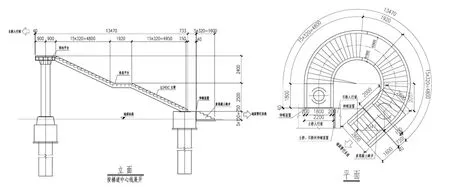
圖1　梯道總體布置圖（單位：mm）

鋼螺旋梯道一般可采用空間梁單元結構模型、空間梁-板混合單元結構模型和空間板單元結構模型。空間梁單元結構模型采用梁單元模擬梯梁，踏步視為橫梁連接兩個梯梁，同樣采用梁單元模擬，此種模型忽略了橫梁與梯梁之間的“蒙皮效應”對提高結構整體性的貢獻，建模過程簡單，便于應用；空間梁-板混合單元結構模型將梯梁視為空間梁單元，踏步按板單元處理，此種模型可準確地模擬踏步的受力情況以及其對梯梁的約束作用，建模過程相對復雜；空間板單元模型將梯梁與踏步均采用板單元模擬，計算結果能準確反映結構受力和變形情況，建模過程復雜，不便于工程應用。為方便工程應用并使計算結果能夠相互驗證，本次計算分別采用空間梁單元結構模型和空間梁-板混合單元結構模型對該梯道進行建模計算，并對計算結果進行分析對比。

2　工程概況

該梯道總體布置如圖1所示；梯道由內外兩片梯梁和踏步組成；梯道中心跨徑為12.4m，最外側跨徑18.8m，最內側跨徑8.1m；在跨中設置休息平臺；梯道內半徑1900m，外半徑3900m；梯道兩側箱梁尺寸為400× 200×16mm；踏步采用L型鋼尺寸為320×150×10mm；根據設計，梯道僅在兩端分別設置橋臺橋墩，休息平臺處不立墩，要求梯道一跨完成；下部結構采用樁柱式橋墩、輕型橋臺，梯梁分別與橋墩、橋臺固結。

3　結構計算與分析

3.1建模計算

梯道采用結構鋼Q345qC（GB/T714-2008）。

作用在該梯道的荷載包括：

⑴恒荷載：①自重，程序自動計入重量，自重系數取-1；②二期恒載：6cm瀝青混凝土，γ=24kN/m3；③欄桿：單側按計。

⑵人群荷載：計算采用兩車道加載；按《城市人行天橋與人行地道技術規范》（CJJ69-95）條文3.1.3.2取用：人群荷載加載長度L按中線跨度13m取值，半橋寬度B=0.9m。

⑶溫度作用：整體溫度作用按±30℃考慮；梯度升溫按照橋面鋼板升溫15℃計算，梯度降溫按橋面板降溫7.5℃計算。

⑷基礎變位：基礎沉降取10mm。

梯道兩端固結。采用容許應力法進行驗算。荷載工況包括：荷載組合1：恒載+人群+支座位移，對應應力提高系數1；荷載組合2：恒載+人群+支座位移，對應應力提高系數1.25。

計算采用有限元軟件Midas/Civil2015（Ver. 8.3.2R1），建立如下兩種模型：模型1——空間梁單元結構模型，如圖2所示；模型2——空間梁-板混合單元結構模型，如圖3所示：

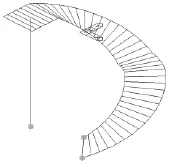
圖2　空間梁單元結構模型

圖3　空間梁-板混合單元結構模型

3.2計算結果分析

根據有限元軟件的計算，提取計算結果如下。

3.2.1模型1應力計算結果

⑴模型1應力計算結果

梯梁剪力和扭矩見附錄；橫梁剪力和扭矩很小，可不考慮彎曲剪應力影響，有效應力可參照圖5。

觀察圖4，梯梁最大拉應力出現在梯梁上端，最大壓應力出現在梯梁底部；梯梁應力由梯梁兩端向跨中休息平臺呈逐漸減小趨勢；應力在休息平臺處有所增加。觀察圖5，橫梁最大應力出現在休息平臺附近；橫梁應力由平臺向梯梁兩端呈逐漸減小趨勢。通過觀察可知，梯梁最不利位置出現在梯梁兩端；橫梁最不利位置出現在跨中休息平臺處。

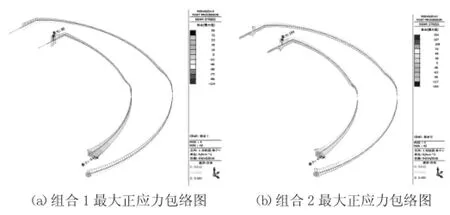
圖4　模型1梯道梁應力包絡圖（MPa）

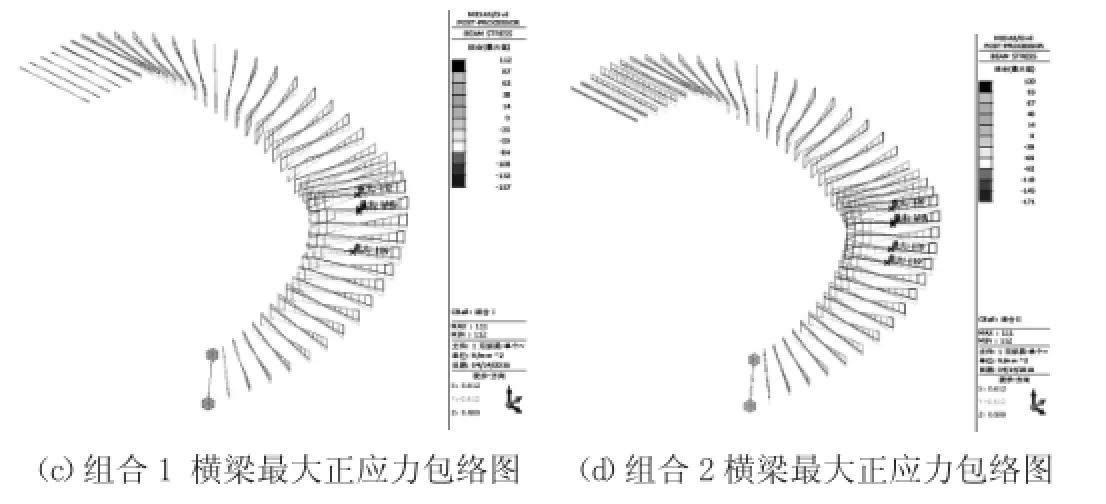
圖5　模型1橫梁應力包絡圖（MPa）

⑵模型2應力計算結果

梯梁剪力和扭矩見附錄。橫梁剪力和扭矩很小，彎曲剪應力對橫梁影響很小。

觀察圖6，梯梁最大拉應力出現在梯梁上端，最大壓應力出現在梯梁底部；梯梁應力由梯梁兩端向跨中休息平臺呈逐漸減小趨勢，變化趨勢比較緩和；應力在休息平臺處增加至與梁端應力接近。觀察圖7，橫梁最大應力出現在休息平臺附近；橫梁整體應力分布較均勻。通過觀察可知，梯梁最不利位置出現在梯梁梁端與跨中休息平臺處；橫梁最不利位置出現在跨中休息平臺處，橫梁應力整體分布均勻。

根據以上計算結果對該螺旋梯道進行驗算，驗算結果如表1所示。

通過表1驗算可知，該螺旋梯道整體計算應力滿足要求。

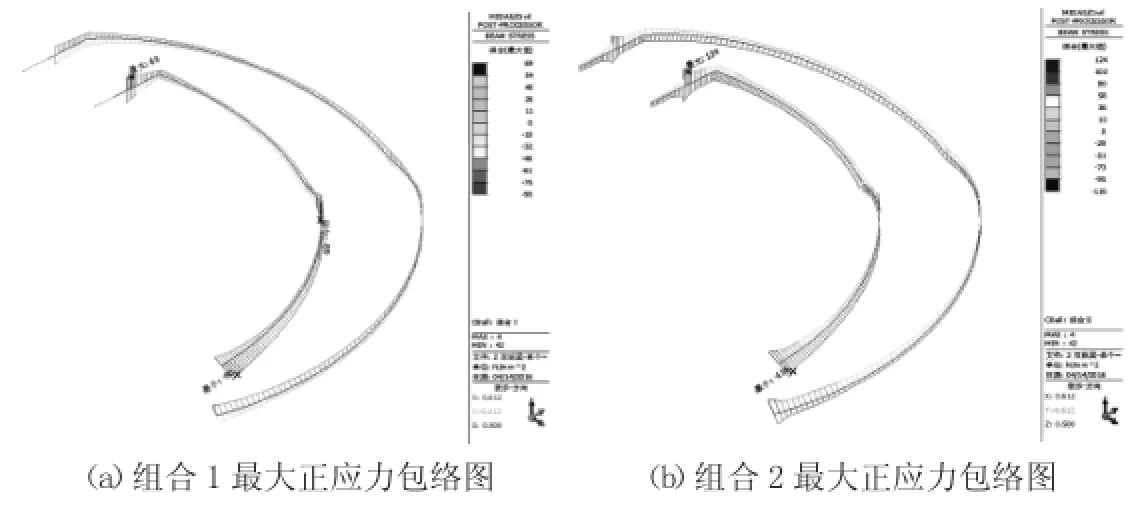
圖6　模型2梯道梁應力包絡圖（MPa）

圖7　模型2橫梁應力包絡圖（MPa）

表1　應力驗算結果

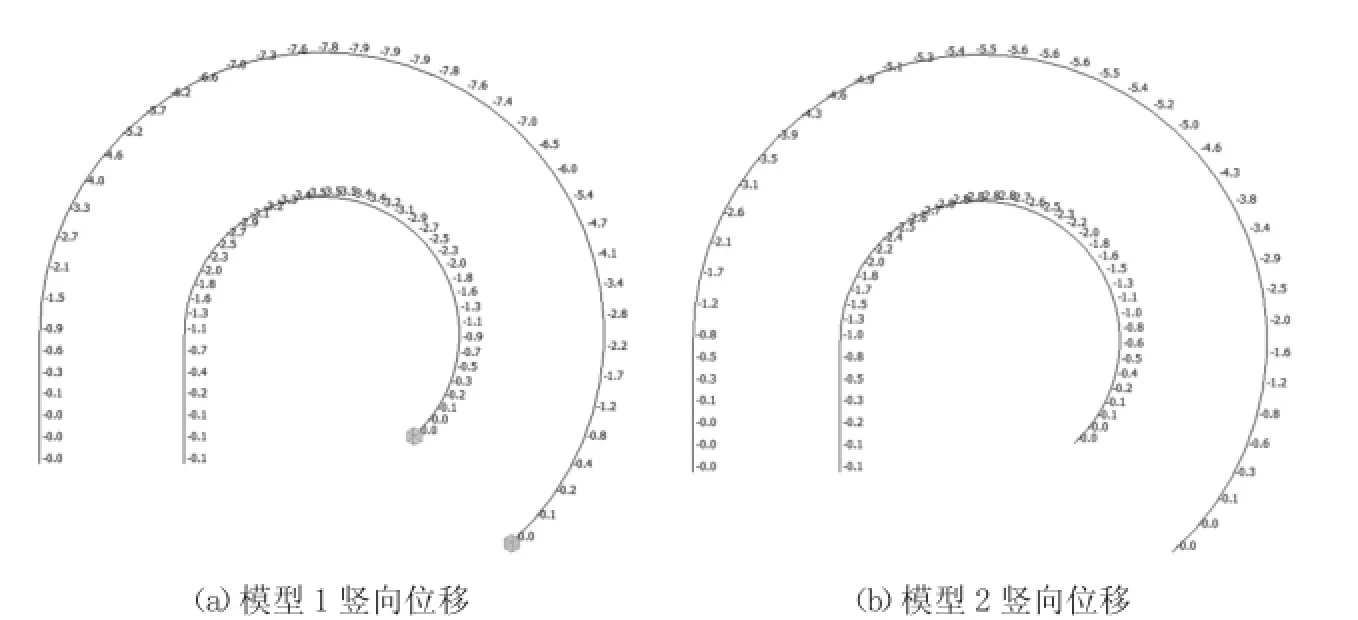
圖8　梯道梁人群荷載豎向位移（mm）

表2　梯道梁人群荷載豎向位移驗算

3.2.2主梁整體剛度分析

觀察圖8和表2，梯道人群荷載作用下最大豎向位移均發生在跨中休息平臺附近；外側梯道梁豎向位移均大于內側梯道；兩種模型計算得到的豎向位移變化趨勢相似；人群荷載豎向位移均滿足規范要求。

3.2.3兩種計算模型比較

觀察圖4和圖6，兩種模型的梯梁應力分布整體一致；最大應力均出現在梯梁兩端；梯梁應力由梯梁兩端向跨中平臺方向呈減小趨勢；觀察圖5和圖7，兩種模型的橫梁最大應力均出現在跨中休息平臺附近；橫梁應力由平臺向梯梁兩端呈逐漸減小趨勢；比較跨中與梁端應力差值，模型1梁端應力明顯大于跨中平臺處應力，而模型2兩處應力則較為接近。觀察表1對比兩種模型的最大應力和有效應力，模型1應力整體大于模型2，這可能是由于“蒙皮效應”的影響，使結構整體應力分布均勻，從而使模型2應力減小。

觀察圖8和表2，兩種模型得到的結構豎向位移變化情況整體一致；而由于忽略截面翹曲的影響，模型1的豎向位移比模型2偏大。

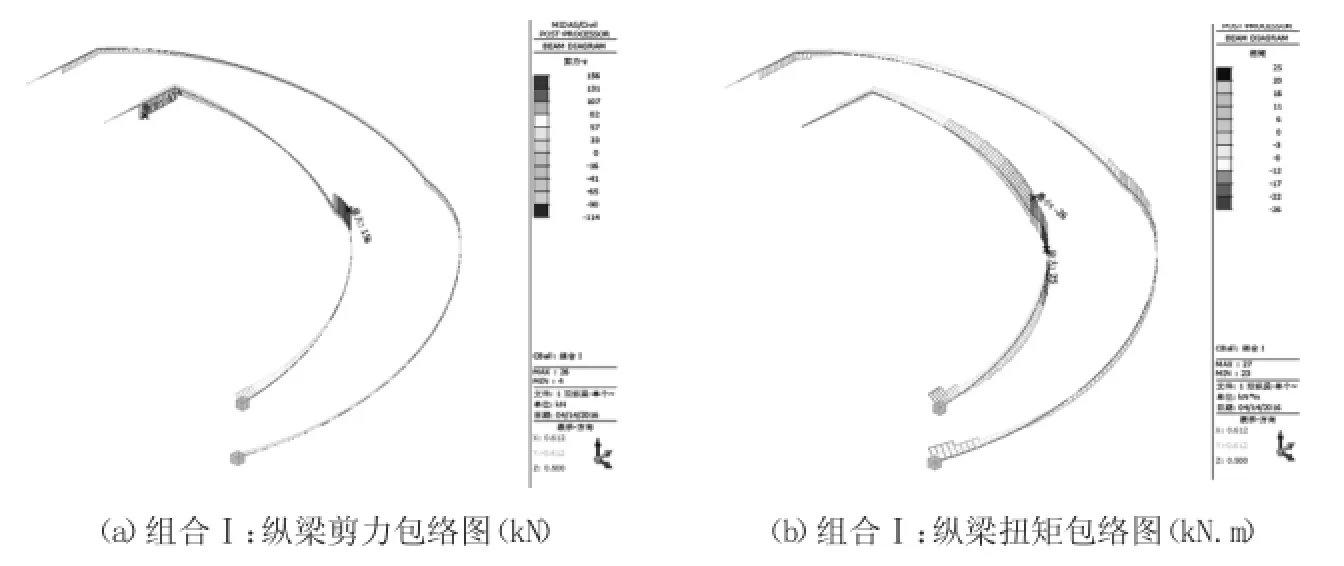
附錄1模型1梯道梁內力圖

附錄2模型2梯道梁內力圖

3.3結論及建議

通過兩種模型對鋼螺旋梯道的計算分析和比較，可得到以下結論及建議：

⑴使用兩種結構模型，即空間梁單元結構模型和空間梁-板混合單元結構模型，計算得到的鋼螺旋梯道應力分布和變形情況基本一致，說明兩種模型計算的正確性。

⑵兩種模型的計算結果表明，該螺旋梯道應力及剛度均滿足規范要求。

⑶空間梁單元結構模型計算得到的應力與位移均比空間梁-板混合單元結構模型大，這可能是因為空間梁單元結構模型對橫梁做了簡化，降低了橫梁對結構整體作用的貢獻。

⑷實際設計中，建議采用空間梁單元模型進行計算，此種計算方法建模過程簡單，所得計算結果偏于安全?！?/p>

［1］桂萍，陳昶.鋼結構旋轉樓梯的結構設計與有限元計算方法［J］.工程建設與設計，2002，（5）：6-10.

［2］王喆，程蓓，申林，等.鋼結構螺旋樓梯的設計［J］.鋼結構，2006，21（5）：22-24.

［3］武韓青，曾德偉，等.鋼螺旋樓梯的計算及設計方法研究［J］.鋼結構，2012（增刊）：645-652.

［4］袁建霞.板式鋼螺旋樓梯的有限元分析及計算方法研究［D］.秦皇島：燕山大學，2005.