無人機飛行控制器及模糊編隊控制器的設計

李倩，雷仲魁

（南京航空航天大學 江蘇 南京　210016）

無人機飛行控制器及模糊編隊控制器的設計

李倩，雷仲魁

（南京航空航天大學 江蘇 南京210016）

文章對無人機編隊控制系統中的單機飛行控制器與編隊飛行控制器分別進行了設計。在單機飛行控制器中加入了加速度控制模塊，將模糊PID控制算法應用于編隊控制器，針對"長機-僚機"模式2架無人機進行了編隊設計仿真。仿真結果表明，單機飛行器通過控制加速度大小可模擬仿真出無人機真實加速情況；編隊控制器通過控制相對距離可實現跟隨編隊以及合理的隊形變化，保持穩定飛行。這種控制方法切合實際，超調量小，系統穩定，滿足設計要求。

無人機；編隊飛行；單機飛行器；模糊PID控制

無人機的編隊飛行主要解決編隊控制［1］的問題，根據特定飛行任務對編隊隊形的要求，需要控制隊形在整個飛行過程中保持不變或在一定誤差范圍內變化。近年來，科學研究者基于仿生學研究，進行了很多關于無人機編隊的研究。比如，利用常規的PID控制方法進行設計的編隊系統［2］，用于雙機編隊飛行的自適應神經網絡控制［3］，用于多無人機編隊的分布式控制［4］等 。本文結合前述研究與無人機實際飛行條件，在原來理想仿真狀態的基礎上，考慮了無人機飛行性能限制，使無人機編隊飛行控制器與實際情況更加吻合，對無人機單機飛行控制器和編隊控制器進行了設計與仿真。

1　無人機飛行控制器設計

假設編隊系統中采用相同的長機和僚機的自動駕駛儀。速度和航向一般采用一階保持器，高度采用二階保持器，則自動駕駛儀［5～6］數學模型表達如下:

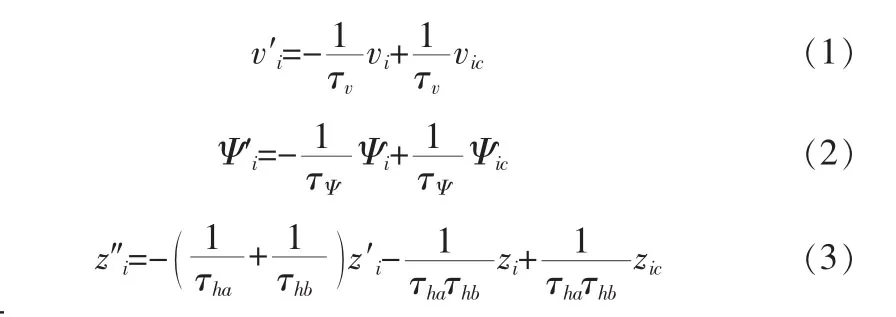
可見，此模型的速度控制模塊不考慮無人機的加速度，而是假設其加速度上限為無限大，而但實際情況是達不到的。因此，為完善設計，需要在無人機速度駕駛模型增加一個加速度模塊。由于MATLAB中的Simulink具有使用方便，調制參數便捷的特點，因此本文采用Simulink模型進行仿真，其速度改進控制模型如圖1所示。可見在原自動駕駛儀基礎上增加了限幅模塊，當加速度需要過大時，仍然使其保持在設定的最大值，以達到仿真要求。

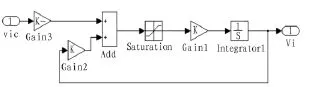
圖1　改進的速度控制模塊

2　無人機模糊編隊控制器設計

兩架無人機在編隊飛行過程中，存在相對運動。本文考慮的編隊模式為“長機—僚機”模式。假設兩架編隊飛行的無人機中，長機為L，僚機為W。在慣性參考坐標系下，長機位置坐標記為L（x1，y1，z1，ψ1），僚機的位置坐標記為W（x2，y2，z2，ψ2），ψ1、ψ2分別為長機和僚機的航向角。同時，在僚機參考坐標系下，長機與僚機實際間隔表示為xr與yr。根據編隊飛行中兩架無人機的幾何關系［5～6］，可推出其編隊飛行的相對運動方程，將1節自動駕駛儀模型代入到該相對運動方程中，再利用小擾動原理對該方程進行簡化，即可得系統的狀態方程為

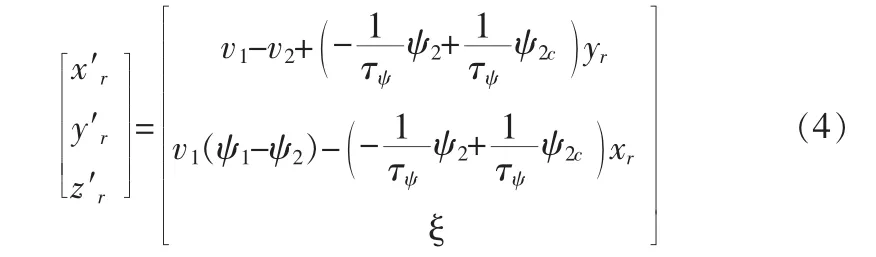
PID控制律是應用廣泛的一種控制方法，但由于實際的無人機編隊系統常容易受到各種復雜因素的影響，傳統的PID控制方法參數整定出來以后就不會再改變，難以適應編隊系統內部參數的隨時變化［7］。而模糊控制屬于自適應控制，能夠很好地適應這種變化，適合處理無人機編隊這種復雜的非線性系統問題。因此本文采取基于自適應模糊PID控制算法設計的控制器。在模糊編隊控制器系統中，線型混合器由速度通道、航向通道和高度通道構成，數學表達為:

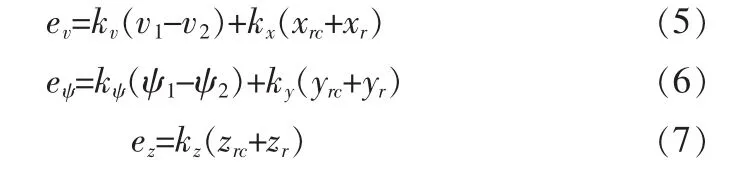
基于模糊 PID算法的控制器是以系統反饋誤差及其變化率為輸入，然后利用模糊規則和控制算法實現PID參數［8］的在線調整。針對無人機編隊控制系統，對速度、航向和高度通道分別設計其基于模糊PID算法的控制器。模糊PID控制器的輸入為誤差e和e′，輸出為 PID參數的增量Δkp，Δki，Δkd。設計時選用高斯函數作為模糊控制器的隸屬度函數，定義各個通道的參數論域，將權值設置為 1，再對模糊推理結果反模糊化即可得到精確的Δkp，Δki，Δkd值。最終結合系統動態設計指標，反復調整控制器中PID的3個參數以達到最優，即可得到各通道控制器的參數。數學表達為

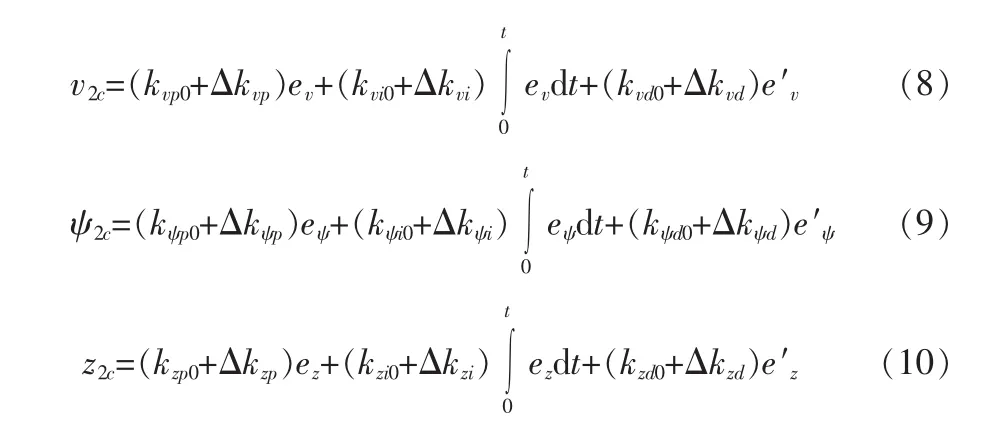
3　仿真結果分析

3.1無人機單機飛行器加速度仿真

本文采用某型號無人機，單機加速度仿真以無人機真實飛行狀態為背景［9］，假設該機加速度為27.7 m/s2（約10 s內速度由0增加到100 km/h），單機飛行器不考慮其他變量，只關注速度變化。仿真時間取60 s，輸入初始速度與控制速度（希望飛機達到速度）。由仿真圖2可知從0加速到100 km/h，約耗時10 s，之后便保持平穩運行；從80 km/h加速到100 km/h，系統約在3 s左右達到響應速度，之后保持平穩運行。由此可見，所設計的單架飛機加速度模型符合設計要求，較好的對無人機自動駕駛儀進行了模型仿真，可用于整個編隊系統。

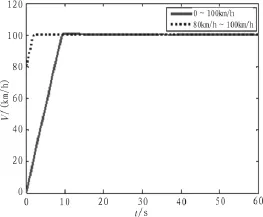
圖2　加速度仿真

3.2無人機編隊仿真

3.2.1仿真初始條件

根據前文整定的控制參數，假設長機與僚機采用同一駕駛儀模型，對編隊控制器采用左菱形編隊隊形進行仿真。由于本文編隊過程適用范圍為松散編隊到緊密編隊的過程，松散集結已完成高度的調整［10］。因此編隊飛行仿真假設2架無人機已飛到同一水平面并保持同一高度飛行，不考慮其高度的變化。仿真初始條件設置為，長僚機X方向初始間隔xrc0=100 m，Y方向初始間隔yrc0=30 m；長僚機最大加速度a=100 m/s2，初始速度都為80 km/h，初始航向角都設置為0。

3.2.2長僚機跟隨狀態仿真

取仿真時間為100 s，編隊時兩機處于同一水平面內，初始條件同上設置。對長機速度v1突然從80 km/h變為100 km/h，航向角ψ1偏轉0.3 rad，進行機動仿真。仿真結果如圖3所示。

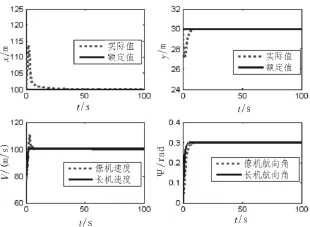
圖3　長僚機跟隨機動仿真

由圖可知，當長機發生機動時，僚機的速度、航向角也隨之發生機動，并且能在短時間內達到穩定收斂狀態。對于xr，yr，在最初幾秒內偏離設定編隊間距，但在短時間內調整后，迅速回到穩定狀態，調整到期望額定間距。由仿真可知，在設定最大加速度值后，速度變化要求滿足實際仿真情況，且整個系統調制時間短，超調量小，可滿足編隊跟隨要求。

3.2.3編隊隊形變化仿真

取仿真時間100 s，要求無人機從左菱形變化到右菱形進行編隊飛行。設定左菱形相對距離為xr=100 m，yr=30 m，右菱形為xr=100 m，yr=-30 m。編隊變換時假設長機速度v1=100 km/h，航向角ψ1=0.3 rad。得到的仿真結果如圖4所示。

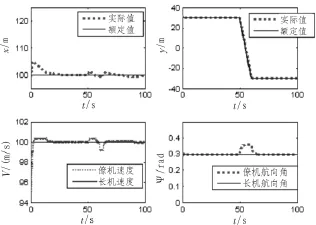
圖4　長僚機編隊變換仿真圖

由仿真圖4可知，僚機是在穩定飛行前進的同時，按設定要求向右進行隊形的調制與變化，速度和航向角都隨之經歷了一些變換并最終回到設定值的過程，完成了y方向間隔的變換調整，實現了左菱形到右菱形的變換。圖5所示為長僚機隊形變化時的間距變化和實時軌跡，更加直觀地表明了僚機能夠較好地完成左菱形到右菱形的隊形變換任務。

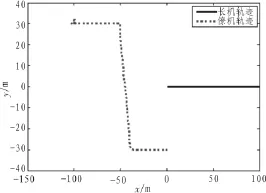
圖5　左菱形變為右菱形的實時軌跡圖

4　結束語

由仿真結果可以看出，單無人機控制器能夠在設定加速度值基礎上模擬實際飛行情況，完成速度的控制；在編隊隊形保持過程中，僚機能夠穩定地跟隨長機機動并保持期望的相對位置；而在編隊隊形變換過程中，僚機依然能夠迅速地跟隨長機的機動動作以及航跡，按照長機與僚機之間的新的期望相對位置指令，迅速地變換編隊隊形并保持指定的隊形繼續飛行，從而實現了行進間的編隊隊形變換。由此表明，該單機控制器以及編隊控制器能夠較好的完成2架無人機的編隊跟隨控制以及飛行過程中隊形變化的控制要求，具有一定參考價值。

［1］田八林，葉正寅，張中荃.無人機自由編隊飛行的補償模糊神經網絡控制［J］.中國民航學院學報，2005，23（6）:10-13.

［2］Pachter M，Azzo J J D，Dargan J L.Automatic Formation Flight Control.J Guidance［C］//AIAA，1994:1380-1383.

［3］劉小雄，武燕，李廣文，等.雙機編隊飛行自適應神經網絡控制設計與仿真［J］.系統仿真學報，2009，21（22）:7211-7214.

［4］李廣文，蔣正雄，賈秋玲.分布式多無人機編隊控制系統仿真［J］.計算機仿真，2010，2（27）:101-103.

［5］S McCamish，M Pachter，J J D'Azzo.Optimal formation flight control［C］.AIAA，1995：1-17.

［6］W Proud Andrew，M Pachter，J J D'Azzo.Close formation flight control［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit Portland:AIAA，1999:1231-1246.

［7］肖笑.基于BCC算法的多機系統PSS參數優化設計［J］.陜西電力，2012（12）：51-54.

［8］周云端，何志勇，趙瑞國.基于遺傳算法的加速度控制PID參數自整定研究［J］.火箭推進，2012（4）：68-71.

［9］張蒙正，鄒宇.美國典型高超飛行器項目研發及啟示［J］.火箭推進，2012（2）：1-8，37.

［10］邱進.一種應用于多斷口光控真空斷路器的同步控制系統的設計與實現［J］.供用電，2015（5）：69-73.

【相關參考文獻鏈接】

［1］楊蕊姣，李志宇，陳喆.雙口RAM在無人機三余度飛控計算機數據交換中的應用［J］.2015，23（11）:102-104.

［2］王文旭，李立，李儼.無人機覆蓋航跡規劃中子區域合并方法設計［J］.2015，23（11）:115-118.

［3］張文博，王惠林，呂勃龍，等.無人機載光電任務設備升降機構的控制器設計［J］.2015，23（14）:152-154.

［4］雷金奎，原丹丹，李海生.基于ARM的雙冗余微小型無人機飛行控制系統的設計［J］.2016，24（1）:162-164.

［5］郭昱津，王道波，路引.某型無人機飛行控制計算機硬件設計［J］.2016，24（3）:50-52.

［6］馬陽.基于改進型Smith預估器的超臨界機組主汽溫模糊控制系統［J］.2014，22（6）:17-19.

［7］毛亮，周成剛，張煜昕，等.模糊AHP在船載測控系統效能評估中應用研究［J］.2014，22（8）:85-88.

［8］陳軒，程月華，姜斌，等.衛星姿態控制系統的模糊控制和容錯控制分配［J］.2014，22（9）:62-64.

［9］程權成，常曉恒.T-S模糊系統非脆弱跟蹤控制器設計［J］. 2014，22（17）:1-4.

［10］曹詩林，王安.吹塑機壁厚控制系統的模糊PID控制器的設計［J］.2014，22（21）:84-87.

Controller design of single UAV and UAVs formation keeping based on fuzzy PID

LI Qian，LEI Zhong-kui
（Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

The article studied for the controller design of single UAV and formation keeping.For the single UAV controller，the controller added the acceleration control module，then，the formation keeping controller based on the fuzzy PID algorithm. Considering two UAVs formation flight in a"leader-follower"configuration，the simulation result shows that the single UAV flight controller can imitate the true flight speed change by controlling the acceleration module，and the formation keeping controller can realize formation keeping and changing by controlling the formation separation distances.The controller is practical，less overshoot and stable，which can meet the design requirements.

UAV；formation flight；single UAV controller；fuzzy PID control

TN03

A

1674－6236（2016）16-0086-03

2015-08-20稿件編號：201508111

李倩（1991—），女，江蘇南京人，碩士。研究方向：無人機編隊控制。