SCA-SVM模型在年徑流豐枯識別中的應用

潘秀昌

(云南省水利水電勘測設計研究院， 昆明　650021)

?

SCA-SVM模型在年徑流豐枯識別中的應用

潘秀昌

(云南省水利水電勘測設計研究院， 昆明650021)

通過4個典型測試函數對一種新型全局優化算法——正弦余弦算法(SCA)進行仿真驗證，仿真結果與粒子群優化(PSO)算法、模擬退火算法(SA)、布谷鳥搜索(CS)算法和人工蜂群算法(ABC)進行對比．利用SCA搜尋SVM最佳學習參數，提出SCA-SVM年徑流豐枯識別模型．以龍潭寨水文站為例進行實例研究，利用月徑流序列均值及標準差構建月徑流分類標準，并基于該分類標準構造樣本對SCA-SVM模型進行訓練及檢驗，利用訓練好的SLC-SVM模型對實例年徑流豐枯進行識別．結果表明：SCA算法尋優精度遠優于SA、CS、PSO和ABC算法，具有調節參數少、收斂速度快、尋優精度高和全局尋優能力強等特點；SCA-SVM模型對訓練及檢驗樣本的識別率均為100%，具有較好的識別效果和精度．

年徑流識別；正弦余弦算法；支持向量機；參數優化

科學合理的年徑流豐枯識別對于水文分析計算、年度用水計劃、水量分配及防洪抗旱具有重要意義．常用的豐枯識別方法有模糊聚類法[1]、投影尋蹤法[2]、集對分析法[3]、模糊-集對分析法[4]以及神經網絡法[5]等．支持向量機(Support Vector Machines，SVM)由于具有“結構簡單”、“克服維數災”及“小樣本優勢”等優點，能較好地克服傳統神經網絡過學習和泛化能力差等不足，在各行業領域具有廣泛應用[6-7]．實踐表明，基于徑向基核函數的SVM在解決識別問題時，懲罰因子C和核函數參數g對SVM模型的識別精度具有關鍵性影響．當懲罰因子C較小時，訓練及檢驗樣本識別率均較低，SVM處于欠學習狀態；當C過大，訓練樣本識別率較高而檢驗樣本識別率較低，SVM處于過學習狀態．核函數參數g越小，訓練樣本識別率越高而檢驗樣本識別率越低，SVM處于過學習狀態；當g較大時，訓練及檢驗樣本識別率均較低，SVM處于欠學習狀態．傳統試湊法、網絡搜索法等選取SVM學習參數的方法已不能滿足實際應用的精度要求．當前，隨著智能優化算法的不斷發展和日趨成熟，粒子群優化(Particle Swarm Optimization，PSO)算法[8]、模擬退火算法(Simulated Annealing，SA)[9]、布谷鳥搜尋(Cuckoo Search，CS)算法[10]和人工蜂群(Artificial Bee Colony，ABC)算法[11]等廣泛用于SVM參數優化，在提高SVM模型性能上取得了較好的效果．正弦余弦算法(Sine Cosine Algorithm，SCA)是文獻[12]于2015年基于正弦余弦函數提出的一種新型優化算法，該算法通過創建多個隨機候選解，利用正弦余弦數學模型來求解最優化問題，能夠探索不同的搜索空間，有效避免局部最優，具有模型簡單、調節參數少、收斂速度快、全局尋優能力強等優點，在函數優化和工程設計領域得到初步應用[12]．

年徑流豐枯特性不僅取決于徑流本身的大小，而且取決于徑流的年內時程分配．本文基于SCA算法及SVM特點，提出SCA-SVM年徑流豐枯識別模型，以龍潭寨水文站年徑流豐枯識別為例進行實例研究．主要步驟為：1)采用4個典型低維測試函數對SCA算法進行仿真驗證，仿真結果與PSO、SA、CS和ABC算法的仿真結果進行對比；2)提出SCA-SVM年徑流豐枯識別模型，參考文獻[5]的方法構建樣本對SCA-SVM模型進行訓練、檢驗以及對實例年徑流豐枯進行識別，并與常規方法識別結果進行比較分析．

1　SCA-SVM識別模型

1.1正弦余弦算法

一般來說，以群體為基礎的優化算法是通過一組隨機解以及更新策略而開始優化迭代過程，并利用目標函數進行反復評價，在保證足夠數的隨機解和優化步驟(迭代)條件下，算法可大大增加獲得最優解的概率．參考文獻[12]，SCA算法提出以下位置更新公式：

(1)

(2)

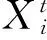
通過式(1)、式(2)組合后的位置更新公式如下：

(3)

式中，r4為rand(0，1)隨機數．

SCA算法中4個主要參數為r1、r2、r3和r4．參數r1決定了下一空間位置區域(或移動方向)，該區域或移動方向可以是候選解和目標解之間的任一空間或之外的空間；參數r2定義了在移動方向上應該移動的步長；參數r3提供了隨機選擇權，即隨機強調(r3>1)或淡化(r3<1)對所定義距離的影響；參數r4表示如何選擇在式(3)中的正弦和余弦分量之間切換．

一種優秀算法應能夠平衡勘探和開采能力，以期遍歷搜索空間內所有區域，并最終收斂到全局最優．為了平衡SCA算法中正弦和余弦函數在搜索范圍內的勘探和開采能力，利用下式來調整參數r1的自適應變化策略．

(4)

式中，t為當前迭代次數；T為最大迭代次數；a為常數．

在理論上，SCA算法基于下述原因能獲得較好的優化性能：(1)針對給出問題，SCA算法創建并改進一系列候選解，其本質有益于全局勘探和局部優化；(2)在探索所定義的搜索空間之外的區域時，正弦和余弦函數返回一個大于1或小于-1的值；(3)當正弦和余弦函數返回值在-1和1之間時，具有較好搜索前景的空間得到開發；(4)SCA算法在定義范圍內運用正弦和余弦函數順利地從勘探階段到開發階段過渡；(5)在優化過程中，全局相對最佳的候選解被存儲為一個可變目標點而不丟失；(6)在優化過程中，候選解總是在當前最佳候選解周圍更新他們的位置，并趨向于搜索空間中的最佳區域．

1.2支持向量機

給定數據集(xi，yi)，xi∈Rn，i=1，2，…，n，xi表示輸入向量，yi表示相應的輸出，依據風險最小化原則，SVM的決策函數為[13]：

(5)

式中，K(xi，xj)=Φ(xi)Φ(xj)為滿足Mercer條件的核函數；ai為對應的Lagrange乘子；b為分類閾值．

本文選擇徑向基核函數(RBF)作為SVM核函數，徑向基核函數表達式為：

(6)

式中，g>0．

因此，基于RBF的SVM識別決策函數為：

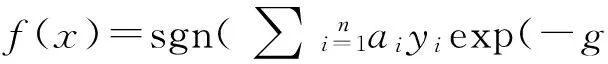
(7)

1.3SCA-SVM算法實現步驟

按上述SCA算法及SVM模型原理可知，SCA算法優化SVM學習參數的思想就是通過SCA算法搜尋一組向量(C，g)，使SVM模型的識別率最高．其實現步驟可歸納如下：

1)參考文獻[5]方法構建樣本，并進行歸一化處理，利用樣本對SCA-SVM模型進行訓練及檢驗．設定懲罰因子C和核函數參數g的搜尋范圍，確定式(8)為參數優化目標(適應度)函數．

(8)

式中，a表示正確識別到某個類別的樣本數；z表示錯誤分類到某個類別的樣本數．

2)初始化算法參數．設置群體數目N、最大迭代次數T、常數a、參數r2、r3；設置算法終止條件，并在解空間內隨機初始化候選解空間位置Xij(i∈[1，2，…，N]，j∈[1，2，…，D])．

3)基于式(8)計算群體候選解的第一次迭代適應度值，找到并保存當前群體中最佳候選解．

4)令t=2，利用式(4)計算參數r1，利用式(3)更新新候選解位置．

5)計算新候選解的適應度值，并與前次迭代最佳候選解的適應度值進行比較．若當前候選解優于前次候選解，則保存當前候選解為最佳候選解；否則，保存上次候選解為最佳候選解．

6)判斷算法是否滿足終止條件，若滿足，則轉到第7)步；否則，令t=t+1，重復執行第5)～6)步．

7)輸出最優候選解適應度值及所處空間位置，即(C，g)值，將(C，g)作為SVM的最佳學習參數對檢驗樣本及實例進行識別．

2　實驗仿真

針對低維極值優化問題，采用4個典型測試函數，見表1．對SCA算法進行仿真驗證，求測試函數的極小值，并與PSO、SA、CS和ABC算法的尋優結果進行比較，見表2．

表1　基準函數

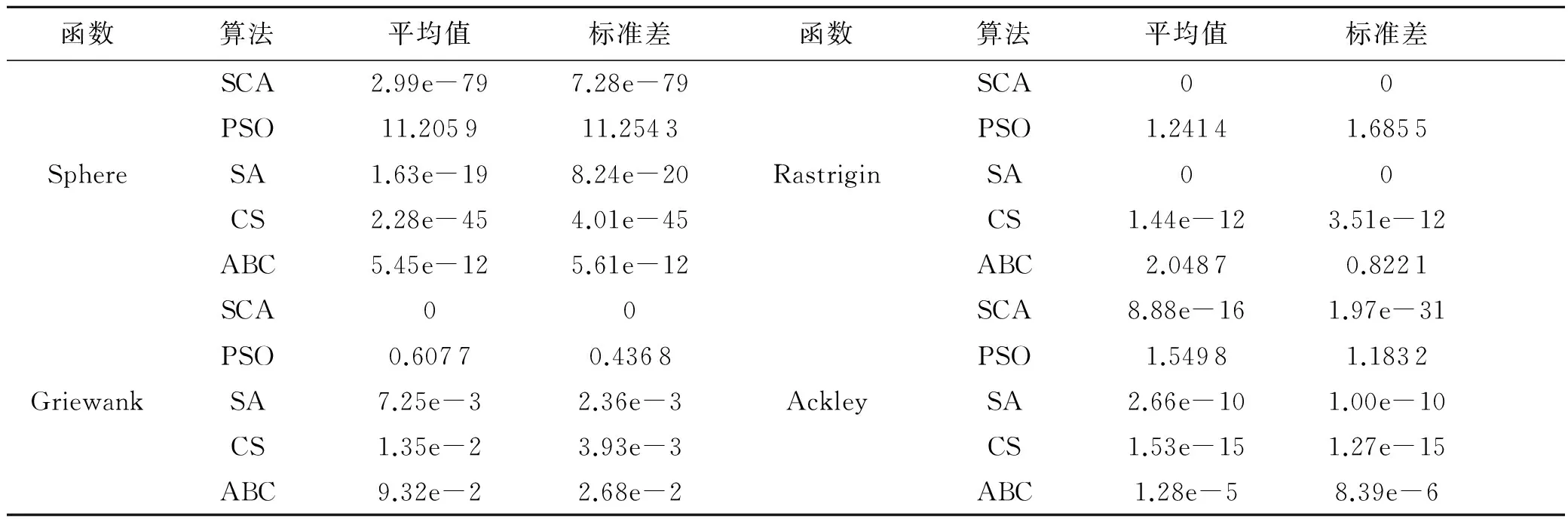
表2　函數優化對比結果

表1中，Sphere為單峰函數，用于測試算法的收斂速度和收斂精度；Griewank、Rastrigin和Ackley為多峰函數，用于測試算法逃逸局部極值能力和全局搜索性能．參考文獻[8-12]，設置實驗參數如下：SCA算法最大迭代次數T=1 000，群體規模N=50，常數a=2，參數r2=2×π×rand()，r3=2×π×rand()．PSO算法最大迭代次數T=1 000，種群規模N=50，ω=1，局部學習因子、全局學習因子c1=c2=2.0．SA算法最大迭代次數T=1 000，種群規模N=50，初始溫度T0=500，終止溫度Tend=0.001，溫度冷卻系數q=0.99．CS算法最大迭代次數T=1 000，鳥窩位置數N=25、發現概率pa=0.25．ABC算法最大迭代次數T=1 000，種群規模SN=50，局部循環次數lc=60．7種算法基于Matlab 2010a用M語言實現，對表1中4個測試函數重復進行20次尋優計算，并從平均值和標準差2個方面進行評估．

1)從表2來看，對于Sphere單峰函數，SCA算法求解精度優于CS、SA、ABC和PSO算法20個數量級以上，表現出較好的收斂精度和收斂速度；對于Griewank函數，SCA算法求解獲得了理論最優值，尋優效果遠遠優于SA、CS、ABC和PSO算法，表現出較好的全局與局部搜索平衡能力；對于Rastrigin函數，SCA、SA算法尋優均獲得了理論最優值，尋優效果明顯優于CS、PSO和ABC算法，表現出較好的全局極值搜索能力；對于Ackley函數，SCA算法獲得了較高的求解精度，尋優精度優于CS、SA、ABC和PSO算法5個數量級以上，具有跳出局部極值的良好性能．

2)綜合比較而言，SCA算法尋優效果優于SA和CS算法；遠優于PSO和ABC算法，具有較好的收斂速度、收斂精度和極值尋優能力．

上述比較表明，SCA算法利用正弦余弦數學模型來求解最優化問題，能夠探索不同的搜索空間，有效避免局部最優，具有調節參數少、收斂速度快、尋優精度高和全局尋優能力強等特點．

3　應用實例

3.1數據來源與月徑流識別標準

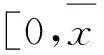
3.2SCA-SVM模型識別結果及分析

1)生成樣本．參考文獻[5]方法構造100個樣本，分別隨機選取60個、40個樣本作為訓練和檢驗樣本，并以各月序列最大流量的5倍作為識別上限值．將1～5作為特枯、枯、中、豐和特豐的識別輸出，并利用式(9)對各月徑流序列進行歸一化處理：

(9)

2)構建模型．在MatlabR2011a軟件環境下，基于libsvm工具箱編程構建12輸入1輸出的SCA-SVM識別模型．SCA-SVM模型參數設置為：SCA部分除最大迭代次數T=100外，其余參數設置均同上；SVM部分懲罰因子C和核函數參數g的搜索空間分別設為1～1 000、0.001～10．

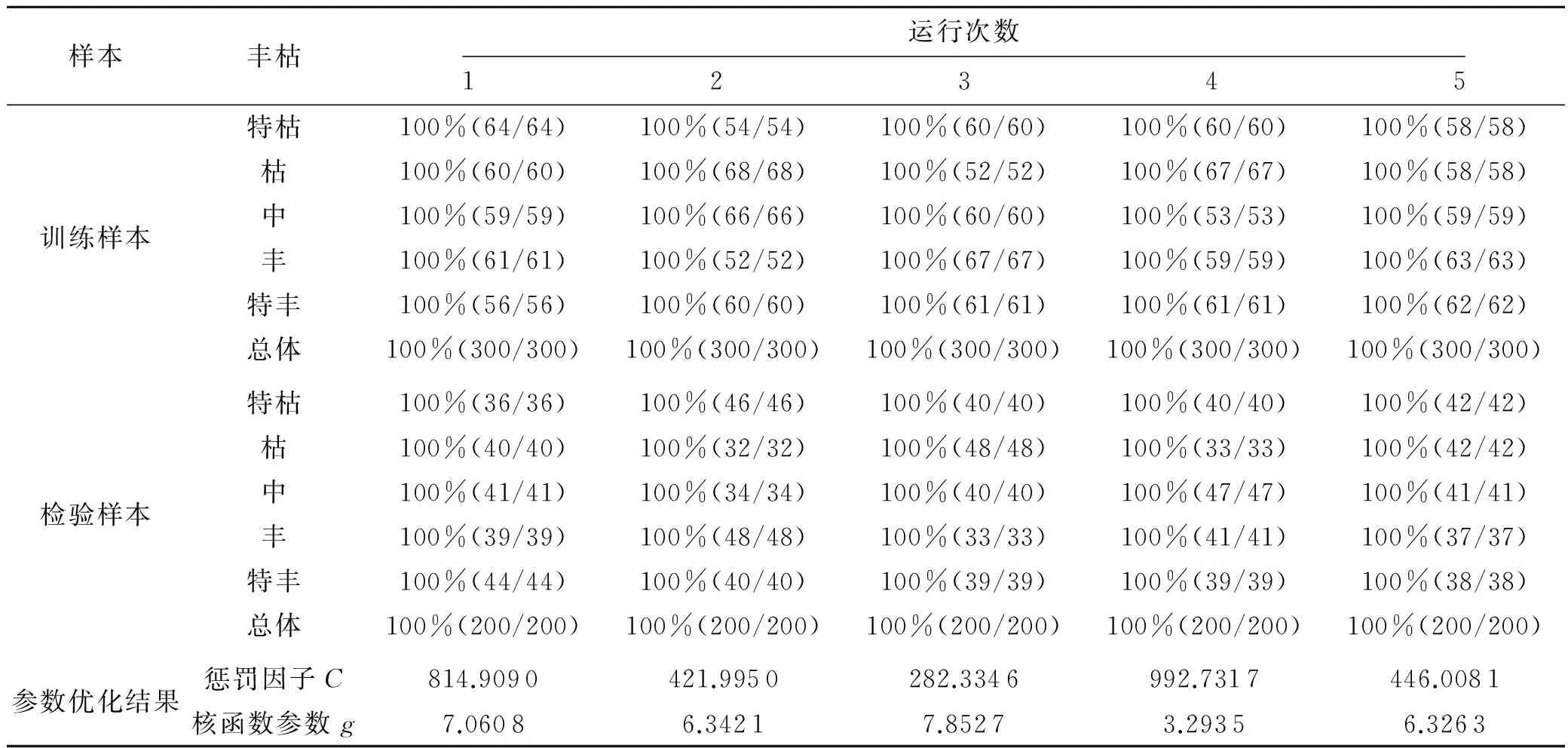
3)SCA-SVM模型訓練與檢驗．利用隨機內插和隨機選取的樣本對SCA-SVM模型進行訓練及檢驗，隨機5次運行訓練及檢驗結果見表3，并給出某次識別過程圖及識別結果圖，如圖1～2所示．

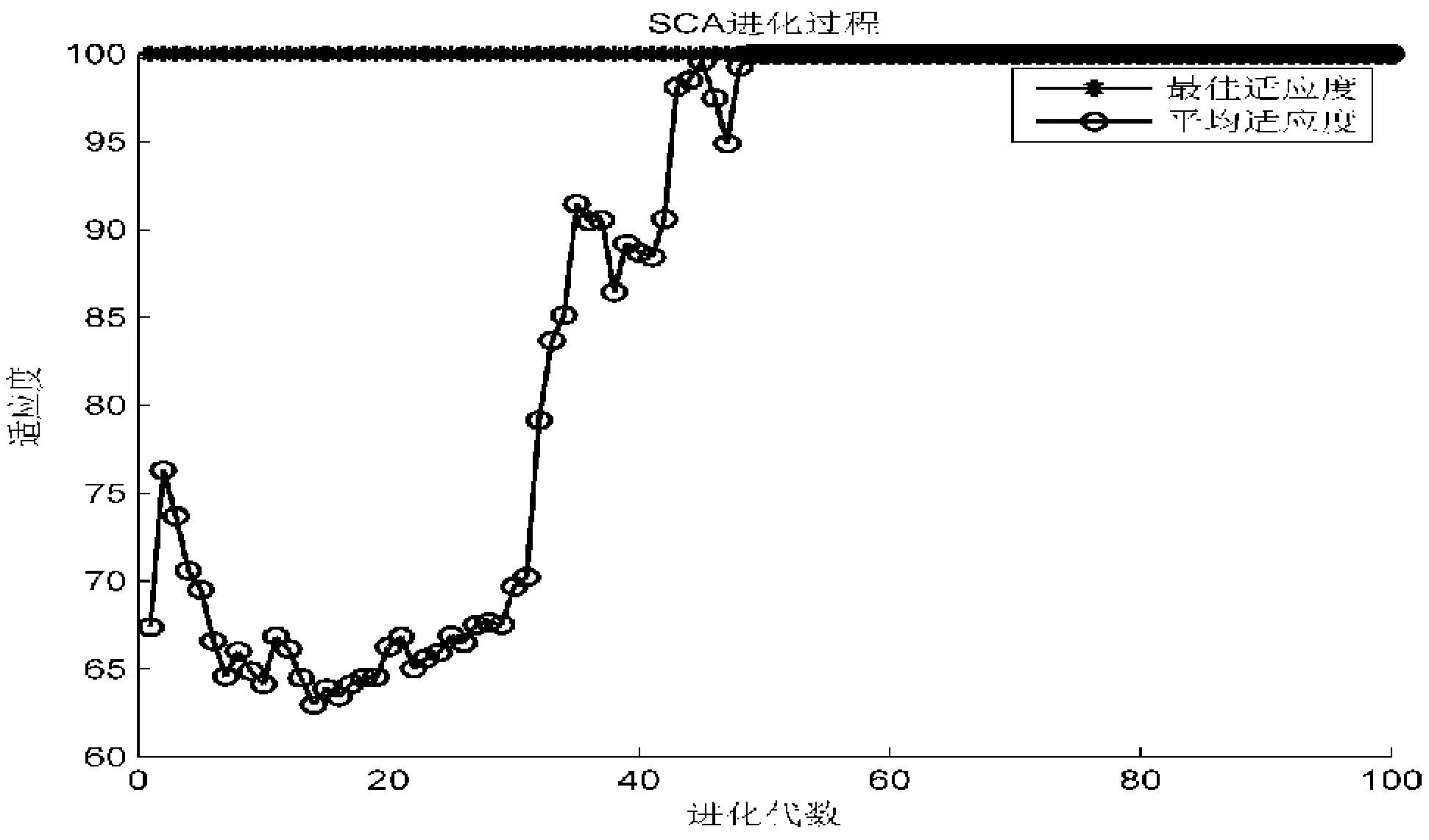
圖1　SCA算法某次尋優進化過程圖

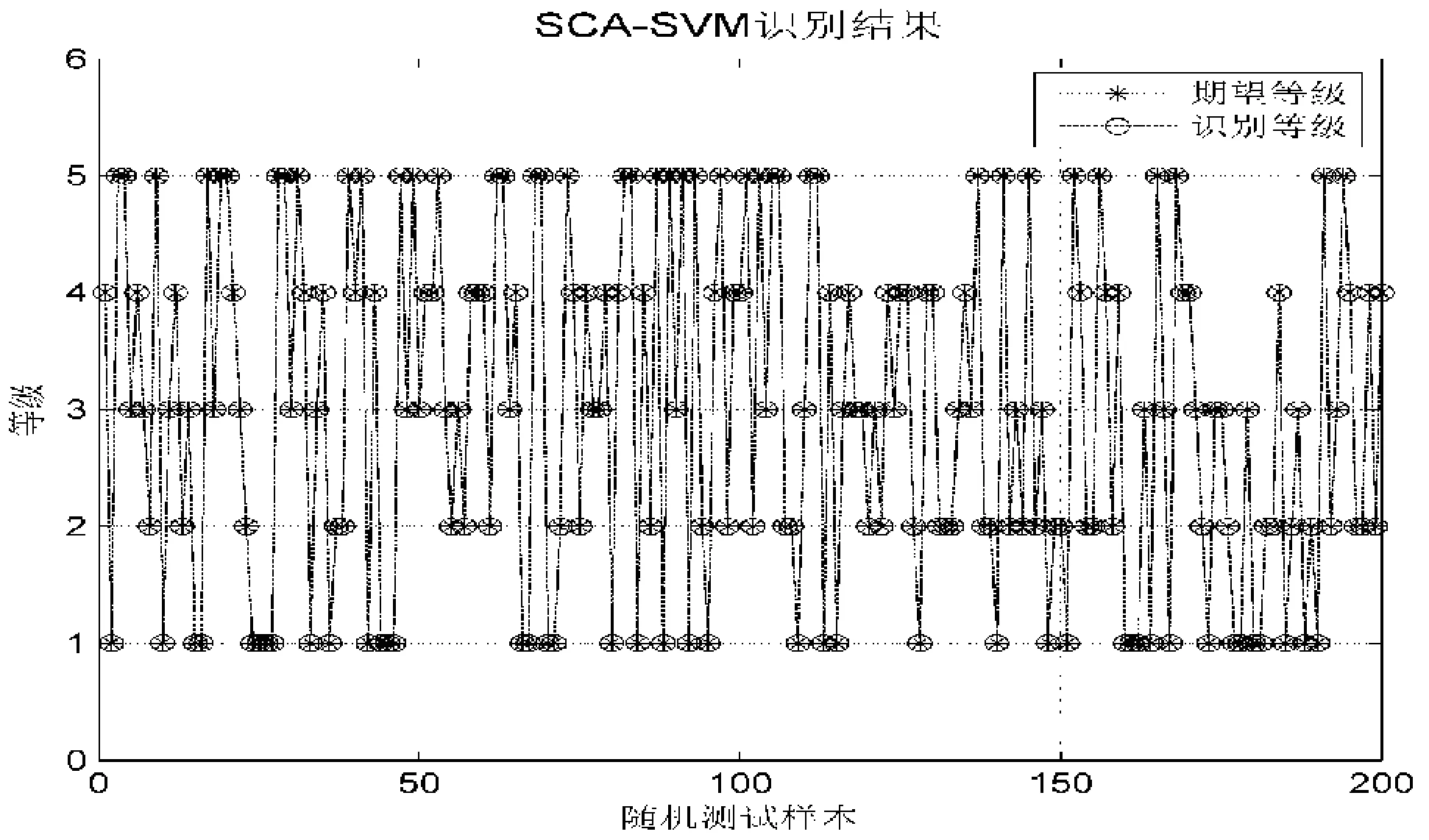
圖2　SCA-SVM模型豐枯識別結果

樣本豐枯運行次數12345訓練樣本特枯100%(64/64)100%(54/54)100%(60/60)100%(60/60)100%(58/58)枯100%(60/60)100%(68/68)100%(52/52)100%(67/67)100%(58/58)中100%(59/59)100%(66/66)100%(60/60)100%(53/53)100%(59/59)豐100%(61/61)100%(52/52)100%(67/67)100%(59/59)100%(63/63)特豐100%(56/56)100%(60/60)100%(61/61)100%(61/61)100%(62/62)總體100%(300/300)100%(300/300)100%(300/300)100%(300/300)100%(300/300)檢驗樣本特枯100%(36/36)100%(46/46)100%(40/40)100%(40/40)100%(42/42)枯100%(40/40)100%(32/32)100%(48/48)100%(33/33)100%(42/42)中100%(41/41)100%(34/34)100%(40/40)100%(47/47)100%(41/41)豐100%(39/39)100%(48/48)100%(33/33)100%(41/41)100%(37/37)特豐100%(44/44)100%(40/40)100%(39/39)100%(39/39)100%(38/38)總體100%(200/200)100%(200/200)100%(200/200)100%(200/200)100%(200/200)參數優化結果懲罰因子C814.9090421.9950282.3346992.7317446.0081核函數參數g7.06086.34217.85273.29356.3263

從表3及圖1～圖2可以看出，SCA-SVM模型隨機5次運行對訓練及檢驗樣本的識別率均為100%，具有較好的識別效果和精度．

4)實例識別結果及分析．利用訓練及檢驗好的SCASVM模型對實例年徑流豐枯特性進行識別，并與文獻[5]MVO-GRNN模型法和常規方法(以年徑流均值為指標采用均值標準差法)識別結果進行比較，見表4．

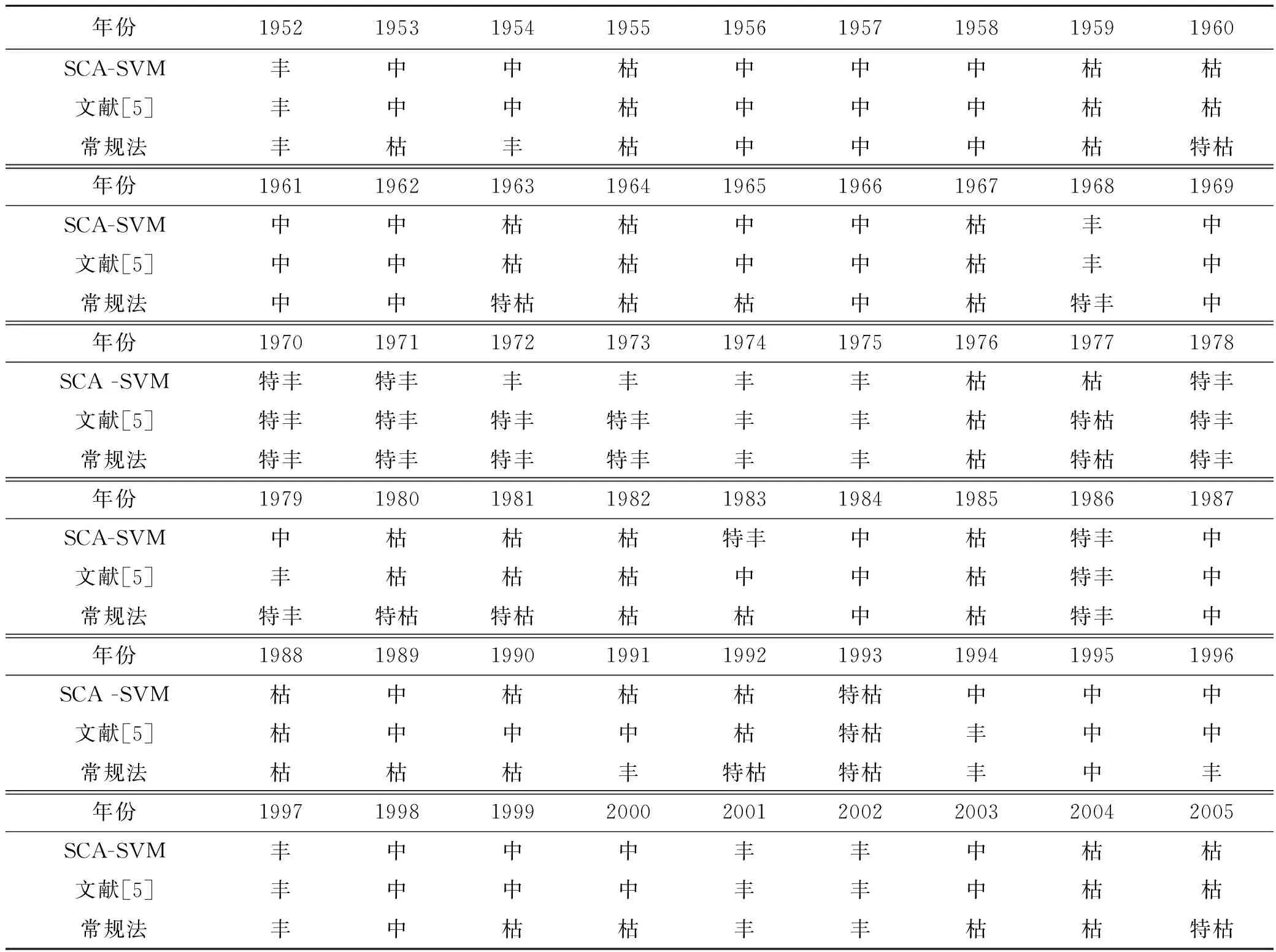
表4　龍潭寨水文站年徑流豐枯識別結果及比較

從表4可以看出，SCA-SVM模型和文獻[5]MVO-GRNN模型法的分類結果基本相同，與常規法的識別結果存在一定的差異．如1979年，SCA-SVM模型識別結果為中水，而MVO-GRNN模型法和常規法分別識別為豐、特豐水年，從年內時程來看，1979年豐水期徑流量占年徑流總量的78%，年內分配較不均衡，識別為中水更合理；又如1983年，SCA-SVM模型識別結果為特豐，而MVO-GRNN模型法和常規法分別識別為中、枯水年，從年內時程來看，1983年枯水期徑流量占年徑流總量的48.2%，幾乎占到年徑流總量的一半，年內分配較均衡，故識別為特豐更合理．從驗證比較結果來看，由于SCA-SVM模型考慮了年徑流本身的大小及年內時程分配信息，其識別結果更科學合理．

4　結　論

驗證了SCA算法的優化性能，提出SCA-SVM年徑流豐枯識別模型，以云南省龍潭寨水文年徑流豐枯識別為例進行實例驗證，并同MVO-GRNN模型法、常規方法識別結果作對比，結果表明：

1)通過4個典型測試函數仿真驗證了SCA算法尋優精度優于SA和CS算法，遠優于PSO和ABC算法，具有收斂速度快、求解精度高、極值尋優能力強等特點．

2)基于月徑流序列均值及標準差構建月徑流分類標準，并利用該分類標準隨機內插和隨機選取樣本對SCA-SVM模型進行訓練及檢驗，使SCA-SVM模型獲得了較好的識別精度．模型及方法具有通用性，可為相關識別研究提供參考．

3)SCA-SVM模型和MVO-GRNN模型法的評價結果基本相同，與常規法的識別結果存在一定的差異．由于SCA-SVM模型不但考慮了徑流本身的大小，而且考慮了年徑流年內時程分配，其識別結果更科學合理．

[1]張軍良，馬光文，張志剛．模糊聚類法在徑流豐枯特性分析中的應用[J]．人民長江，2009，40(7)：11-13．

[2]趙太想，王文圣，周秀平．一種徑流豐枯分類新方法研究[J]．人民黃河，2006，28(5)：12-13．

[3]王文圣，向紅蓮，李躍清，等．基于集對分析的年徑流豐枯分類新方法[J]．四川大學學報：工程科學版，2008，40(5)：1-6．

[4]丁小玲，周建中，陳璐，等．基于模糊集合理論和集對原理的徑流豐枯分類方法[J]．水力發電學報，2015，34(5)：4-9．

[5]崔東文，吳盛華．MVO-GRNN模型在年徑流豐枯分類中的應用[J]．人民珠江，2015，36(6)：50-54．

[6]孫艷，刀海婭．自適應變異粒子群算法與支持向量機在農業用水預測中的應用[J]．水資源與水工程學報，2015，26(3)：231-236．

[7]崔東文．支持向量機在水資源類綜合評價中的應用研究——以全國31個省級行政區水資源合理性配置為例[J]．水資源保護，2013，29(5)：20-27．

[8]白春華，周宣赤，林大超，等．消除EMD端點效應的PSO-SVM方法研究[J]．系統工程理論與實踐，2013，33(5)：1298-1306．

[9]魏勝．基于模擬退火算法支持向量機在枯水期月徑流預測中的應用[J]．水資源與水工程學報，2015，26(2)：135-138．

[10] 賴錦輝，梁松．一種新的基于GCS-SVM的網絡流量預測模型[J]．計算機工程與應用，2013，49(21)：75-79．

[11] 于明，艾月喬．基于人工蜂群算法的支持向量機參數優化及應用[J]．光電子·激光，2012，(2)：374-378．

[12] S． Mirjalili， SCA：A Sine Cosine Algorithm for Solving Optimization Problems[M]． Knowledge-based Systems， in press， 2015．

[13] 孫莉，徐琪．混合和聲搜索算法優化SVM的訂單優先權評價[J]．計算機工程與應用，2015，51(12)：241-245．

[責任編輯王康平]

Application of SCA-SVM to Annual Runoff Wet-Dry Identification

Pan Xiuchang

(Yunnan Institute of Water & Hydropower Engineering Investigation, Design & Research, Kunming 650021, China)

Through four test functions of a New Global Optimization Algorithm - SineCosine algorithm (SCA) performed simulation, simulation results and particle swarm optimization (PSO) algorithm, simulated annealing algorithm (SA), Cuckoo search (CS) algorithm and artificial bee colony algorithm (ABC) were compared. SCA search support vector machine(SVM) use the best learning parameters proposed SCA-SVM years of runoff recognition model. Taking the hydrological Station in Longtan Village for example, the use of monthly runoff series mean and standard deviation of monthly runoff build taxonomies and classification based on the standard configuration of the sample SCA -SVM model for training and testing, the use of trained SLC-SVM model examples of runoff for years to identify, recognize the results of the conventional identification methods were compared. The results show that：SCA optimization algorithm accuracy is much better than SA, CS, PSO and ABC algorithm with adjustable parameters small, fast convergence and high precision and optimization of Strong global search ability; SCA-SVM model for training and testing samples recognition rate was 100%, with good recognition performance and accuracy.

annual runoff identification；sine cosine algorithm；support vector machine(SVM)；parameter optimization

2016-05-17

國家水體污染控制與治理科技重大專項(201307102-006-01)；院士工作站建設專項(2015IC013)

潘秀昌(1982-)，男，工程師，主要從事水利水電、水資源規劃和水利水電征地移民設計等工作．E-mail：325865343@qq.com

10.13393/j.cnki.issn.1672-948X.2016.04.002

P333

A

1672-948X(2016)04-0006-06