考慮流量約束的碳存儲管道運輸網絡優化

尹宇起，李　清，楊　斌，胡志華

(上海海事大學科學研究院，上海 201306)

?

考慮流量約束的碳存儲管道運輸網絡優化

尹宇起，李清，楊斌，胡志華

(上海海事大學科學研究院，上海 201306)

針對實現碳存儲技術的大規模應用問題，提出以管道網絡為基礎的碳存儲網絡設計模型.通過將管道運輸的特點與最小生成樹方法相結合，提出考慮節點流量的連續節點最小樹方法，建立對應的碳存儲網絡設計模型.對連續選址的收集點進行編碼，采用遺傳算法求解模型得到添加連續節點的最小樹網絡.通過以上海市為背景的碳存儲網絡設計實驗可知，考慮節點流量的連續節點最小樹網絡優于一般最小生成樹網絡，而且針對遺傳算法中交叉概率及收集節點編碼長度分別設置實驗，分析了算法中參數的選取對求解結果的影響.

碳捕獲與封存；碳存儲；最小生成樹；遺傳算法；管道網絡

0　引言

溫室氣體增加所產生的溫室效應導致全球變暖的現象已成為國際社會關注和討論的熱門問題.碳捕集與封存(Carbon Dioxide Capture and Storage，CCS)作為減少溫室氣體排放的重要手段成為全球研究熱點，管道運輸是該技術得以實施的關鍵環節[1].由于碳源與碳匯在區域分布上的不均衡，在碳存儲網絡的設計過程中如何實現節點間液態CO2的管道物流成為碳存儲網絡設計的重點.

碳存儲網絡中碳源點的特點：CCS網絡中的熱電廠、水泥廠、化肥廠、鋼鐵廠等碳源的數目較大且多分布在工業園區和城市周邊.每個碳源的CO2排放量巨大，如一個裝機容量為500 MW的發電廠每年需要輸送4～5 Mt的CO2[2].液態CO2需要在特定條件下運輸，如文獻[3]通過對離岸碳存儲鏈CO2運輸的研究得出整個系統的最優運輸條件.

本文設計的碳存儲網絡指在管道網絡的基礎上，增加碳捕獲和碳封存環節構成的能夠完成碳存儲完整流程的網絡系統.管道網絡結構的決策成為碳存儲網絡設計問題的關鍵，本文采用節點流量的連續節點最小樹網絡，即在最小生成樹(Minimum Spanning Tree，MST)網絡的基礎上，構建滿足管道網絡設計的新型網絡結構.針對影響管道網絡建設成本的管道長度和管道直徑2個主要因素，在連續節點最小生成樹網絡問題中增加節點的流量，約束優化管道路徑的選取.在最小生成樹模型的基礎上建立滿足問題要求的新型最小樹網絡模型，采用遺傳算法進行求解，得到優于一般最小生成樹模型的管道網絡.

1　碳存儲與管道網絡

根據NETL(National Energy Technology Library)的統計資料，世界上正在運行和計劃建設的CCS項目(包括單純的碳捕獲項目)已有247項.由于CCS技術的目標是實現CO2永久性或半永久性隔離，而且海洋封存技術目前還不成熟，且涉及海底生態、法律等諸多方面的問題[4]，因此上述已經實施的CCS項目中CO2的封存方式主要是地質封存.

CO2的管道運輸技術已經成熟，通過改進管道技術壓縮成本的空間不大，因此優化碳存儲網絡，設計高效的運輸網是降低網絡成本的關鍵.國內外相關研究人員已經開始進行碳存儲網絡設計和優化的研究.[5-12]將該源匯匹配問題歸結為一個具有多背包性質的組合最優化問題，建立CCS源匯匹配數學模型，采用結合貪婪算法的混合遺傳算法求解模型.J.Morbee等人[6]在網絡設計過程中，首先使用k-均值聚類法減少網絡中節點數，然后應用Delaunay三角網得到運輸管道的預選方案，最后運用InfraCCS工具以新確定管道成本為目標設計最優網絡.M.K.Chandela等人[8]討論了干線管道的潛在經濟性，由于地理位置影響封存成本，通過主干線管道運輸CO2到一個成本低的封存點使網絡更經濟.由于碳存儲網絡建設的資金限制及經濟最優化，一些學者運用動態網絡規劃的思想研究碳存儲網絡.孫亮等人[11]提出基于GAMS的源匯匹配動態規劃模型，借鑒Delaunay三角網來構造潛在運輸路徑，將源匯匹配問題簡化為混合整數規劃問題，應用GAMS/CPLEX進行建模求解.R.S.Middletona等人[12]通過對網絡的成本、建設和環境問題進行詳細全面的建模，構建了考慮時空優化的SimCCSTIME模型，研究如何以及何時部署大規模CCS的基礎設施.上述文獻主要從數學規劃及動態規劃的角度研究CO2運輸管道網絡問題.

設計管道網絡也可以應用圖論中的最小生成樹方法[7，13-14]，運用模擬退火算法和最小支撐樹算法對潛在CO2匯點進行離散選址決策，并確定最優網絡布局.本文在已有最小生成樹文獻基礎上選址新節點并考慮節點的流量，從而通過設計管道網絡，優化管道路徑的選取及管道直徑的確定.

2　問題定義

2.1問題描述與分析

本文所設計的碳存儲網絡是以管道網絡為基礎結合碳捕獲和碳封存環節構成的網絡系統.針對管道網絡設計問題的要求，提出以下假設：(1)問題中將碳源點及碳匯點確定為圖中節點，其中碳源點捕獲并輸出CO2，碳匯點作為管道的終端節點(根)封存CO2；(2)節點間管道的衡量指標包括長度和直徑，管道網絡設計的目標是實現管道網絡的權重值(與管道長度及直徑有關)最小化；(3)每個碳源點只有一條輸出管道，但可以有多條輸入管道；(4)在建成管道網絡中，CO2總是由各碳源點發出沿著所在路徑輸送到碳匯點，即網絡中的邊(弧)方向，然而初始連通圖中這種方向性并不存在；(5)添加的收集點本身的輸出量為0.

在管道網絡的建設中，管道的長度與直徑決定工程建設的投入.由于碳源點的分布具有區域廣泛性及無規律性，大規模的碳存儲網絡中管道網絡建設的投入巨大，如何選擇管道路徑及確定管道直徑、優化管道網絡建設成本成為碳存儲網絡設計的關鍵問題.本文管道路徑的選擇可由最小樹模型網絡確定，并且各段管道的直徑由流經管道的CO2流量確定，因此管道的長度與直徑在路徑選取后即可確定.此時問題的目標是管道網絡建設成本最優，即管道的長度與直徑成為管道路徑選取的目標.

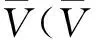
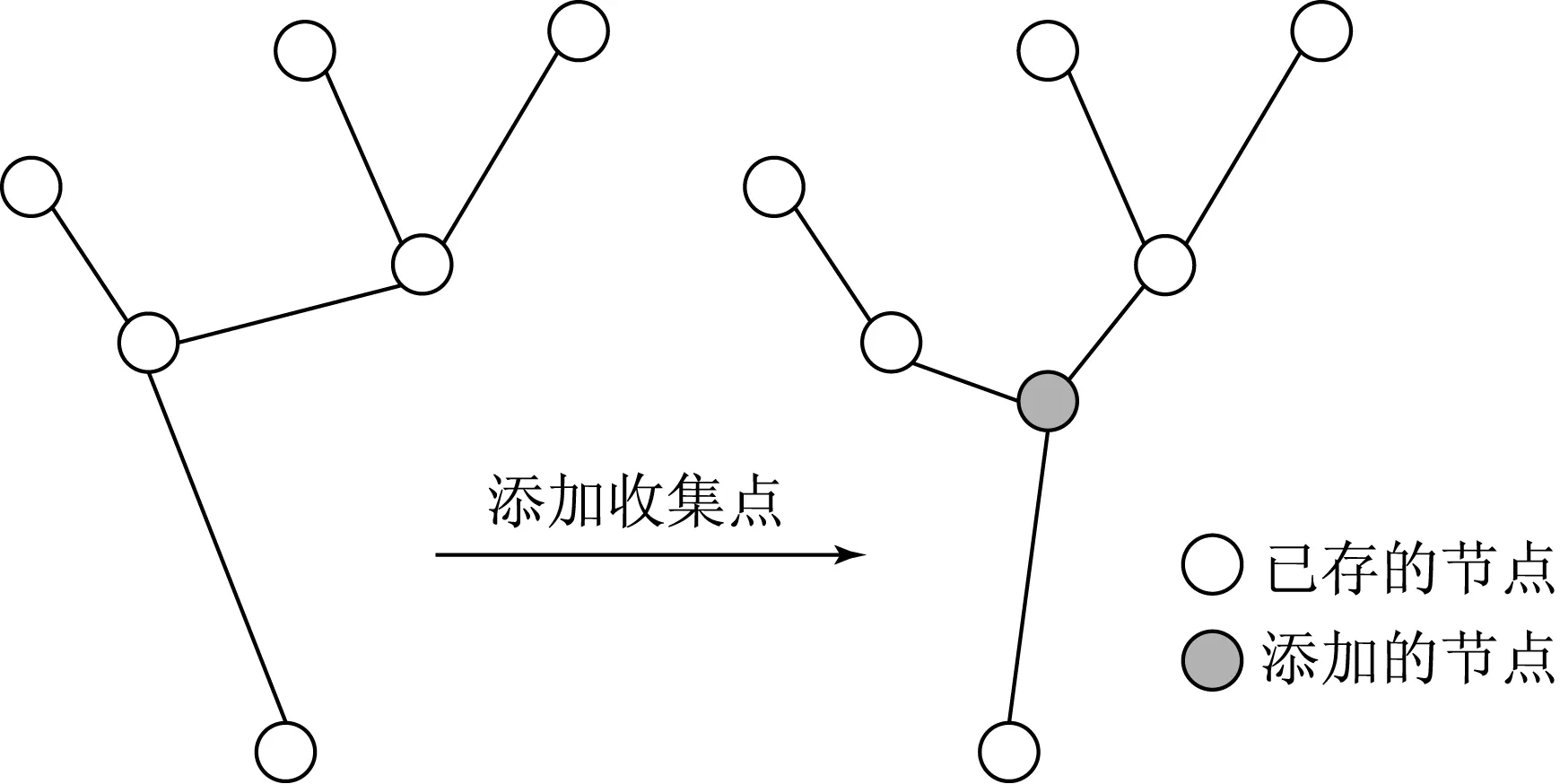
圖1　最小生成樹轉化為連續節點最小樹示意圖

通過上述的問題描述可知，此時最小樹網絡中的賦權值包括邊的長度(管道長度)和節點的輸出量(碳捕獲量).為了設計最優的碳存儲管道網絡，本文在最小生成樹網絡模型[M1]的基礎上，考慮節點的輸出量構建最小樹模型[M2].通過選址新節點更新管道網絡的可選路徑，構建連續節點最小樹模型[M3].本文采用了函數w(d，f)量化問題目標，即碳存儲管道網絡建設成本最小化，其中d表示管道長度，f表示管道流量.

2.2符號定義

假設無向圖以G=(V，E)表示，有向圖以T=(V，A)表示.模型涉及的參數與變量符號如下.

2.2.1集合與索引

(a)i，j=1，2，…，n，表示碳源的索引；

(b)k=1，2，…，m，表示添加的連續節點的索引；

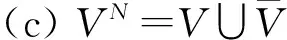
(d)GN=(VN，EN)，表示擴展后圖的無向圖.

2.2.2參數

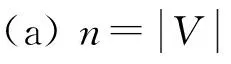
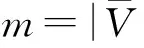
(c) (Xi，Yi)，i∈V，表示碳源點所在位置的坐標；

(d)Ci，i∈V，表示碳源點i需要運輸的二氧化碳量；

(e)Dij，(i，j)∈E，表示碳源點i與j間的距離；

(f)AS表示圖S的邊集，其中S為圖G=(V，E)的任意子圖.

2.2.3變量

(a)xij，(i，j)∈EN，變量為0～1，邊(i，j)∈EN被選則為1，否則為0；

(b)yij，(i，j)∈AN，變量為0～1，弧(i，j)∈AN被選則為1，否則為0；

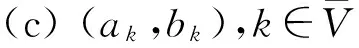
3　模型

3.1一般最小樹模型

求解以管道距離為權重的最小生成樹模型[M1]，其中根據生成樹網絡的性質——邊數等于節點數減1且不含圈，確定一般最小生成樹模型的約束.

(1)

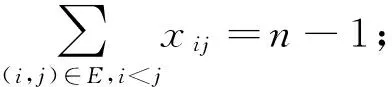
(2)

(3)

xij∈{0，1}，?(i，j)∈E.

(4)

模型中：(1)式表示管道總長度最短；約束(2)式表示最小生成樹網絡中連通的邊數為n-1條；約束(3)式表示最小生成樹網絡中不含圈；約束(4)式表示變量xij為0～1的變量.

3.2節點流量最小生成樹模型

由問題假設(4)可知，在樹形管道網絡構建完成后，無向的樹形圖G=(V，E)可以看做有向樹形T=(V，A)圖(弧的方向與CO2的流向一致)，其中弧的選取yij，(i，j)∈A與邊的選取xij，(i，j)∈E的關系為

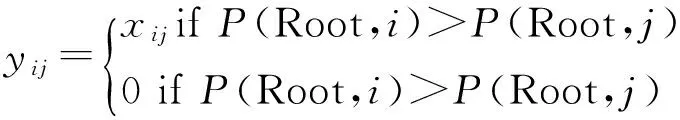
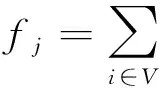
(5)

s.t.(2)與(3)式

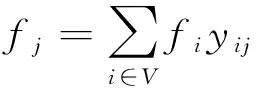
(6)

wij=fi·Dij，?i，j∈V；

(7)

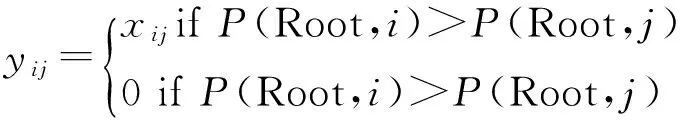
?i，j∈V；

(8)

xij，yij∈{0，1}，?i，j∈V.

(9)

模型中：(5)式為目標函數表示考慮節點流量的最小生成樹網絡賦權值最小；約束(6)式表示節點流量的累加公式；約束(7)式表示賦權值函數公式；約束(8)式表示無向圖與有向圖最小樹間邊(弧)的關系；約束(9)式表示變量xij與yij變量為0～1.

3.3連續節點最小生成樹模型

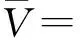
(10)

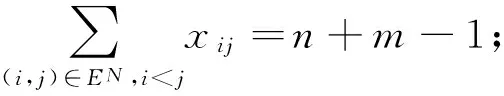
(11)

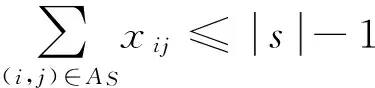
(12)

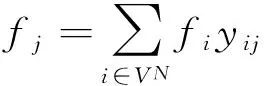
(13)

wij=fi·dij，?i，j∈VN;

(14)

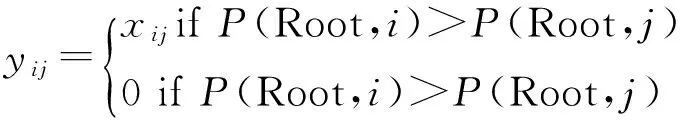
?i，j∈VN;

(15)

?i，j∈VN;

(16)

(17)

xij，yij∈{0，1}，?i，j∈VN;

(18)

(19)

模型中：約束(10)式為目標函數表示考慮節點流量的最小生成樹網絡賦權值最小；約束(11)式表示最小生成樹網絡中連通的邊數為n+m-1條；約束(12)式表示最小生成樹網絡中不含圈；約束(13)表示節點流量的累加公式；約束(14)式表示賦權值函數公式；約束(15)式表示無向圖與有向圖最小樹間邊(弧)的關系；約束(16)式表示添加節點后碳源點i與j間的距離；約束(17)式表示添加節點的數目；約束(18)式表示變量xij與yij變量為0～1；約束(19)式表示ak與bk取值連續.

4　算法

4.1遺傳算法的整體流程

Procedure：添加連續節點的最小生成樹;

Input：碳源的數目及坐標、添加節點的數目、遺傳算法參數;

Output：添加節點坐標及最小樹的長度;

Begin

t←0，

基于實數編碼的方法初始化P(t)，

基于實數編碼的方法評價P(t)，

While(不滿足終止條件)do

使用交叉算子以P(t)產生交叉子代C(t)，

使用變異算子以P(t)產生變異子代C(t)，

求解最小樹的長度，以此評價C(t)，

使用輪盤賭規則從P(t)和C(t)中選擇染色體組成P(t+1)，

t←t+1；

Output：添加節點坐標及最小樹的長度;

End.

4.2編碼和解碼方法

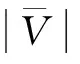
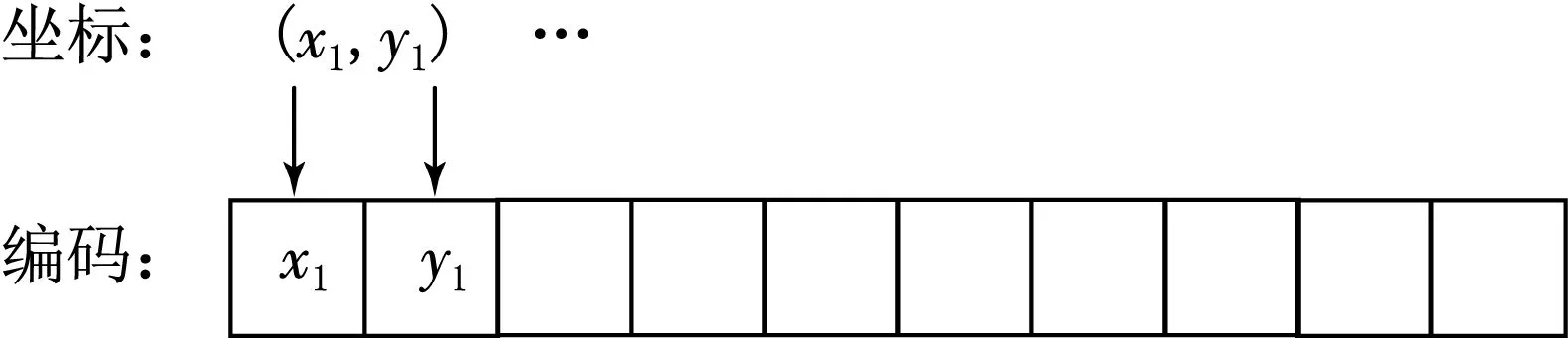
圖2　遺傳算法中編碼示意圖

4.3交叉算子

分散交叉算子偽代碼如下：

Procedure:分散交叉算子；

Input：父代p1[]，p2[]，編碼長度L；

Output：交叉子代c[]；

Begin

i←0，

Whilei≤Ldo，

If rand(i)=1，

c(i)←p1(i)，

else

c(i)←p2(i)，

i←i+1；

Output：交叉子代c[]；

End.

交叉算子求解過程見圖3.

4.4變異算子

均勻變異算子偽代碼如下：

Procedure:均勻變異算子；

Input：父代p[]，編碼長度L，變異概率MR，編碼取值范圍(Low，Up)；

Output：交叉子代c[]；

Begin

Span=Up-Low；//實數編碼區間長度，

Fori=1 toL，

生成隨機數R，

IfR>MR，

生成隨機數Rs，

c(i)=Low+Rs·Span，

Else，

c(i)=p(i)；

Output：交叉子代c[]；

End.

圖4　變異算子求解示意圖

變異算子的求解示意圖見圖4，其中第3個基因被選擇為變異基因.

5　實驗部分

5.1算例數據與算法參數

(1) 算例數據

以上海市為背景設計碳存儲網絡，選取46個碳排放企業作為碳源點且在沿海區域選取1點作為虛擬匯點以便于擴展為離岸碳存儲.節點流量在區間[5，15]內隨機生成.源匯點坐標已知，節點間直線距離表示需要建設管道的長度，連續節點的選取數目根據實驗要求選取.

(2) 算法參數

遺傳算法中主要參數：種群規模為20；迭代次數為200；實驗過程中交叉概率與變異概率若無實驗設置說明，則選取交叉概率為0.8、變異概率為0.10.

5.2實驗設計與結果

為了驗證模型及其對應遺傳算法的可行性，本文設計的實驗見表1，實驗1求解后的結果見表2.

表1　實驗目的及實驗設計

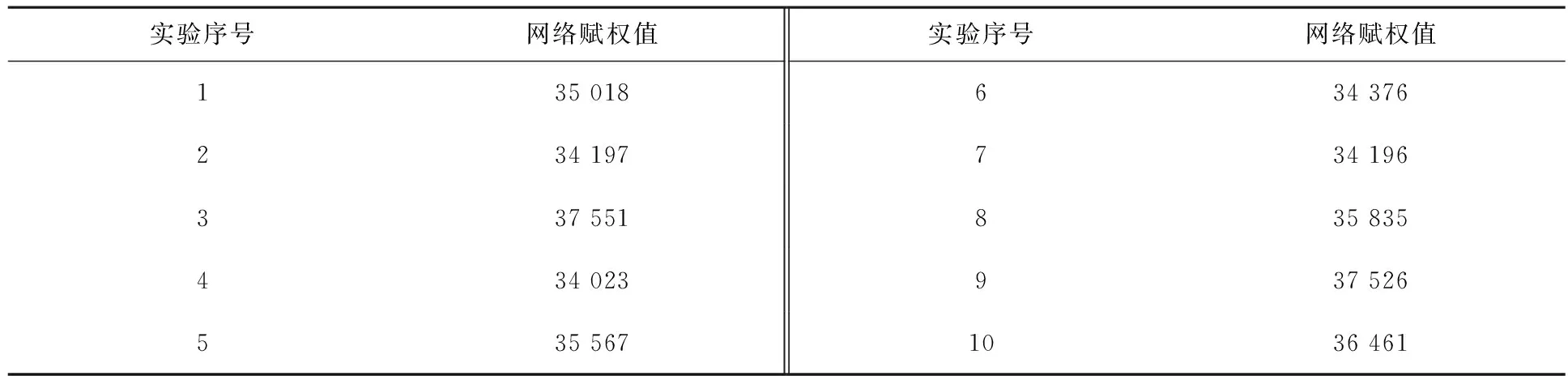
表2　實驗1求解后的結果

5.3實驗分析

(1) 實驗1中求解[M2]得到覆蓋全部碳源的管道網絡的權值為44 257.采用遺傳算法對[M3]求解10次，發現添加新的節點作為管道網絡中的收集點優于未添加節點最小生成樹的實驗結果，見表2.此次實驗中[M2]的實驗結果的平均值為35 475，最小與最大的差值為3 528，然而在現有遺傳算法設置條件下，無法確定何種因素影響[M3]的實驗結果的波動.在模型的求解結果中我們可以發現并非每一添加的收集點都是有效的，如圖5所示.

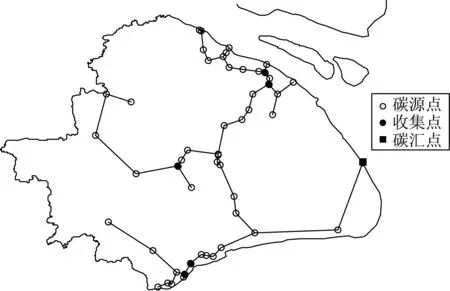
圖5　實驗1中[M3]的求解結果

(2) 根據實驗2求解結果得到圖6，首先添加節點數目不同使得實驗結果的中位值呈現波動性趨勢，添加5個節點時實驗結果的中位值最優；其次，添加節點數目的不同對應的實驗結果的范圍相似，添加5個節點時的優勢解分布密集.

(3) 根據實驗3求解結果得到圖7，首先交叉概率的變化使得各概率條件下的多次實驗的中位數呈現類似拋物線的形狀，交叉概率為0.9時取得較優實驗結果的概率更高；其次，實驗結果中位數的變化趨勢也是實驗結果取值范圍的變化趨勢.

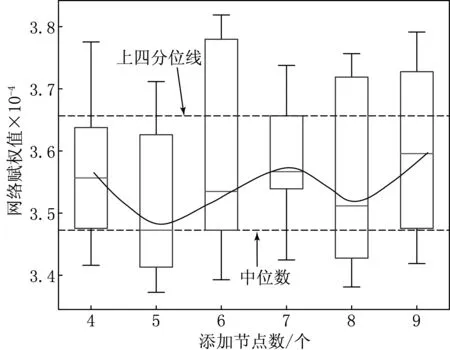
圖6　實驗2求解得到關于網絡賦權值箱形圖

圖7　實驗3求解得到關于網絡賦權值箱形圖

綜上可知，由添加連續節點的最小樹模型[M3]得到的管道網絡優于一般最小生成樹模型[M2]，因此[M3]具有可行性.由于添加的節點中存在無效收集點，在[M3]的最小樹基礎上將無效添加點剔除后才會得到最終的管道網絡.在使用遺傳算法求解[M3]的過程中，算法設置極為重要.通過算例實驗發現：(1)交叉概率與實驗結果間存在近似凸性，通過調整交叉概率可以使實驗結果更優，如上述算例中采用0.9的交叉概率；(2)添加節點數目對實驗結果的范圍影響不大；(3)增加添加節點數目的改變使得求解值呈現波動型變動.

6　結語

為實現碳存儲技術的大規模應用，需要構建完整的碳存儲網絡.本文以管道網絡為基礎構建碳存儲網絡，其中將碳捕獲環節和碳封存環節抽象為碳存儲網絡的節點，采用考慮節點流量的連續節點最小樹模型與遺傳算法相結合的方法求解新型的管道網絡.在新型的管道網絡中，通過添加連續的收集點使得管道網絡的柔性增加，并且考慮碳源點的CO2輸出量量化管道直徑，最后由算例實驗可知，考慮節點輸出量的連續節點最小樹模型得到優于一般最小生成樹模型的管道網絡，驗證了連續節點最小樹模型的可行性.同時，通過算例實驗對遺傳算法中的設置進行相應的討論，為模型與算法的結合及應用提供了理論上的支持.然而求解后發現添加的節點中存在無效收集點，文中并未考慮碳匯點的選擇問題.

[1]李昕. 二氧化碳輸送管道關鍵技術研究現狀[J]. 油氣儲運，2013，32(4)：343-349.

[2]拉克利，李月.碳存儲與封存[M]. 北京：機械工業出版社，2010:278.

[3] NAM H，LEE T，LEE J，et al. Design of carrier-based offshore CCS system：plant location and fleet assignment[J]. International Journal of Greenhouse Gas Control，2013，12：220-230.

[4]王建秀，吳遠斌，于海鵬. 二氧化碳封存技術研究進展[J]. 地下空間與工程學報，2013，9(1)：81-90.

[5]李永，陳文穎，劉嘉. 碳收集與封存的源匯匹配模型[J]. 清華大學學報(自然科學版)，2009，49(6)：894-896.

[6]MORBEE J，SERPA J，TZIMAS E. Optimized deployment of a European CO2transport network[J]. International Journal of Greenhouse Gas Control，2012，7：48-61.

[7]劉巍，董明. 碳封存網絡的規劃模型及求解算法研究[J]. 工業工程與管理，2011，16(6)：128-132.

[8]CHANDELA M K，PRATSONB L F，WILLIAMS E. Potential economies of scale in CO2transport through use of a trunk pipeline[J]. Energy Conversion and Management，2010，51(12)：2825-2834.

[9]MIDDLETONA R S，KUBYB M J，BIELICKIC J M. Generating candidate networks for optimization：The CO2capture and storage optimization problem[J]. Computers，Environment and Urban Systems，2012，36(1)：18-29.

[10]MIDDLETONA R S，BIELICKIB J M. A scalable infrastructure model for carbon capture and storage：SimCCS[J]. Energy Policy，2009，37(3)：1052-1060.

[11]孫亮，陳文穎. 基于GAMS的CCUS源匯匹配動態規劃模型[J]. 清華大學學報(自然科學版)，2013，53(4)：421-426.

[12]MIDDLETONA R S，KUBYB M J，WEIB R，et al. A dynamic model for optimally phasing in CO2capture and storage infrastructure[J]. Environmental Modelling & Software，2012，37：193-205.

[13]ANDRé J，AURAY S，WOLF D D，et al. Time development of new hydrogen transmission pipeline networks for France[J]. International Journal of Hydrogen Energy，2014，39(20)：10323-10337.

[14]WANG Y，DUAN M，FENG J，et al. Modeling for the optimization of layout scenarios of cluster manifolds with pipeline end manifolds[J]. Applied Ocean Research，2014，46：94-103.

(責任編輯：石紹慶)

Carbon storage pipeline transport network optimization considering flow constraints

YIN Yu-qi，LI Qing，YANG Bin，HU Zhi-hua

(Scientific Research Academy，Shanghai Maritime University，Shanghai 201306，China)

The paper offers to the pipeline network-based carbon storage network design problems. By combining the characteristics of the pipeline with the minimum spanning tree(MST) method，the paper establishes the carbon storage network design model with using a continuous-node MST method considering the node output. Encoding the continuous-node of location，and adopting genetic algorithm to solve our model，we can achieve the minimum spanning tree with adding new node. The experiment，designing Shanghai’s carbon storage network，shows that the MST network with continuous-node is better than that without continuous-node. The experiment about the crossover probability，mutation probability and the collection node length coding of genetic algorithms，shows respectively influence on the results from them.

CCS；carbon storage；minimum spanning tree；genetic algorithm；pipeline network

1000-1832(2016)03-0067-07

2015-03-17

國家自然科學基金資助項目(71471109)；交通運輸部科技項目(2015328810160)；上海市科委科研計劃項目(14DZ2280200，14511107402)；上海市教委科研創新項目(14YZ100)；上海市曙光計劃項目(13SG48)；上海市科委科技創新行動計劃項目(14170501500)；上海市自然科學基金資助項目(15ZR1420200)；教育部人文社會科學研究青年基金資助項目(15YJC630145，15YJC630059)；上海海事大學研究生創新基金資助項目(2014ycx013).

尹宇起(1991—)，男，碩士研究生，主要從事綠色物流、管道運輸研究；胡志華(1977—)，男，博士，副教授，主要從事港航與物流運作優化、社會科學計算實驗、計算智能研究.

U 172[學科代碼]520·60

A

[DOI]10.16163/j.cnki.22-1123/n.2016.03.013