模糊聯盟合作對策τ值及其計算方法

楊靛青,李登峰*

(福州大學經濟與管理學院,福建福州 350108)

模糊聯盟合作對策τ值及其計算方法

楊靛青,李登峰*

(福州大學經濟與管理學院,福建福州 350108)

針對現實合作中存在模糊聯盟的情況,利用Choquet積分定義了模糊聯盟合作對策τ值,證明了其存在性、唯一性和其他重要性質,討論了其和模糊核心的關系,并給出凸模糊聯盟合作對策τ值的計算公式.最后通過一個算例說明該τ值的有效性與合理性.研究發現,基于Choquet積分的模糊聯盟合作對策τ值是對清晰聯盟合作對策τ值的擴展,而清晰聯盟合作對策τ值僅是其特例.特別地,對于凸模糊聯盟合作對策,其τ值計算過程可以簡化.

模糊聯盟合作對策;Choquet積分;τ值;對策論;模糊集

1　引　言

τ值、Shapley值[1]和Banzhaf值[2]等都是常見的合作對策單值解.1981年,Tijs[3]用幾何方法首次提出了擬均衡合作對策τ值,并證明了它與核心有密切的關系;Driessen[4]引入分歧函數,給出了擬均衡對策τ值的精確表達式,并討論了其具有有效性、個體合理性等性質和公理化方法,從而說明了τ值作為分配方案時的公平合理性;Bilbao等[5]研究了擬陣合作對策下τ值的計算方法和性質;Casas-mendez等[6]利用Owen聯盟結構的思想,提出了具有聯盟結構的合作對策τ值,對τ值進行公理化刻畫并討論了其在破產對策、機場對策等方面的應用;安世虎[7]考慮合作對策中聯盟結構受到限制的情況,構造了準擬陣合作對策τ值,并將該方法與擬陣合作對策Shapley值進行比較;侯東爽等[8]定義了廣義特征函數下合作對策τ值,利用概率有效性、S均衡下的相對不變性和限制成比例性證明了τ值存在的唯一性,并討論了核心和τ值的關系.以上關于τ值的討論主要集中在經典合作對策上,可以處理在清晰聯盟條件下的合作利益分配問題.但現實中,由于環境變動、可調配資源不確定等因素,局中人可能以模糊聯盟的形式參與合作,如何利用τ值理論方法處理這種模糊聯盟合作利益分配問題,顯然不同于清晰聯盟合作對策的情況,因此有必要對模糊聯盟合作對策τ值的計算方法和性質進行研究.

模糊聯盟合作對策研究關注的重要問題之一是如何描述不同模糊聯盟的合作支付函數.目前,該研究的重要分支就是利用Choquet積分方法對清晰聯盟合作對策下的支付函數進行模糊拓展,并提出基于Choquet積分的模糊聯盟合作對策分配方案.Tsurumi等[9]較早引入Choquet積分方法,提出了模糊聯盟合作對策Shapley值,這類函數具有單調性、連續性等一些良好性質;譚春橋等[10,11]提出了基于Choquet積分的合作對策模糊延拓方法,討論了這種模糊延拓的性質,研究了其與經典合作對策Shapley值、核心的關系;在此基礎上,譚春橋[12]進一步對基于Choquet延拓的區間模糊聯盟合作對策Shapley值進行了研究,證明了該Shapley值的存在性,并給出Shapley值的解釋表達式;Li等[13]通過和文獻[9]的計算方法進行比較分析,給出了模糊聯盟合作對策Shapley值的一種簡單表示方式;孟凡永等[14]提出了基于Choquet積分的模糊聯盟合作對策Banzhaf值,討論了此類對策Banzhaf值的性質和公理化方法.從文獻上看,基于Choquet積分的模糊聯盟合作對策Shapley值、Banzhaf值都有深入研究,成果較多,理論體系較完善,但對基于Choquet積分的模糊合作對策τ值的研究則鮮有報道.

為此,本文在前人研究的基礎上探討了基于Choquet積分的模糊聯盟合作對策τ值的計算方法和性質,利用Choquet積分方法,定義基于Choquet積分的模糊聯盟合作對策τ值,討論此類合作對策τ值的存在性和唯一性,研究此類τ值的相關性質并證明其和模糊核心的關系.特別針對凸模糊聯盟合作對策,簡化了其τ值計算公式.最后通過一個合作生產的實例來說明基于Choquet積分的模糊聯盟合作對策τ值的合理性和有效性.研究結果表明,基于Choquet積分的模糊聯盟合作對策τ值將合作對策τ值的應用范圍從{0,1}n清晰聯盟拓展到[0,1]n模糊聯盟.該τ值是清晰聯盟合作對策τ值的一般化表示形式,其滿足的性質延續了清晰聯盟合作對策τ值的性質,進一步說明它是清晰模糊合作對策τ值的模糊拓展,而清晰聯盟合作對策τ值是其特例.基于Choquet積分的模糊聯盟合作對策τ值為解決在模糊環境下局中人合作利益分配問題提供了一種新方法.

2　清晰聯盟合作對策τ值的定義及性質

清晰聯盟合作對策可表示為一個序對＜ N,v＞,其中N={1,2,...,n}為局中人集合,v為清晰聯盟合作對策的支付函數,即v:N → R且滿足v(?)=0.記G(N)為清晰聯盟合作對策的集合. 記M(v)=(M1(v),M2(v),...,Mn(v))為合作對策v的上值向量,每個分量滿足Mi(v)=v(N)-v(N{i}). Mi(v)可視為局中人i可期望得到的最大支付.m(v)=(m1(v),m2(v),...,mn(v))為合作對策v的下值向量,每個分量滿足,其中S?N?.mi(v)可視為局中人i可期望得到的最小支付.為方便起見,將N{i}簡寫成Ni,v({i})簡寫成v(i),v(S∪{i})簡寫成v(S∪i).

定義2若v∈Gqb(N),則

清晰聯盟合作對策τ值是一個函數τ:Gqb(N)→Rn,滿足下列性質[4]:

2)個體合理性:對于任意i∈N,有τi≥v(i);

3)對稱性:設π是N的一個排列,對于任意i∈N,有τπ(i)=τi;

4)啞元性:設S?Ni,若v(i)=v(S∪i)-v(S),則τi=v(i);

5)替換性:對于任意i,j∈N與聯盟S?N{i,j},若v(S∪i)=v(S∪j),則τi=τj;

6)策略等價下的共變性:設v∈Gqb,若存在一個對策w滿足條件:當a＞0和d∈Rn時,對任意S?N都有

7)限制成比例性:若M(v)=λv,則τ和M(v)成比例.

3　基于Choquet積分的模糊聯盟合作對策

模糊聯盟合作對策可表示為一個序對＜Fn,v′＞,其中N={1,2,...,n}為局中人集合,Fn用于表示局中人集合N上的模糊聯盟集合[0,1]n,v′為n人模糊聯盟合作對策的支付函數,即v′:Fn→R.記G0(N)為模糊聯盟合作對策的集合.用e?=(0,0,...,0)表示空聯盟,eS=(s1,s2,...,sn)滿足當i∈S?N時, si=1,否則si=0,這樣eS表示:S集合中的局中人完全參與聯盟,NS集合中的局中人完全不參與聯盟. eN=(1,1,...,1)表示大聯盟,e{i}表示局中人單干形式,簡寫成表示為局中人集合N上的模糊聯盟,si∈[0,1]表示模糊聯盟中局中人i的參與水平,模糊聯盟也可表示為當T?N時,.將簡寫成.實值支付函數表示為模糊聯盟合作時可期望獲取的支付,滿足v′(e?)=0.當si只取1時,模糊聯盟就退化為清晰聯盟,相應的模糊聯盟合作對策就退化為清晰聯盟合作對策.因此,模糊聯盟合作對策是清晰聯盟合作對策的擴展,而清晰聯盟合作對策是模糊聯盟合作對策的特例.

定義3設v′∈G0(N).如果對任意S1,S2∈Fn,有

則稱v′是凸的(超模),記凸模糊聯盟合作對策的集合為FGcov(N).注意當si只取1時,則v′退化成(清晰聯盟)凸合作對策,記Gcov(N)為凸合作對策的集合.

定義4對于非空集M上所有有界非負可測函數f:M→R+,函數f關于v的Choquet積分定義[11]為

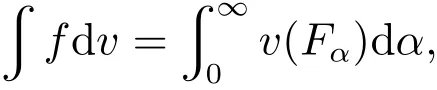
其中Fα={x|f(x)≥α}(α∈[0,∞))為函數f的α截集.

若非空集合M={x1,x2,...,xm},則函數f可以表示成離散形式f(x1),f(x2),...,f(xm),將它們按照單調不減次序可排列為

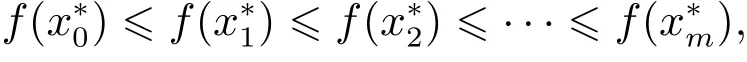
其中{x*1,x*2,...,x*m}為非空集合M中的元素{x1,x2,...,xm}依據上述單調不減排列的重排形式.于是, Choquet積分可簡化表示為

其中f(x*0)=0.

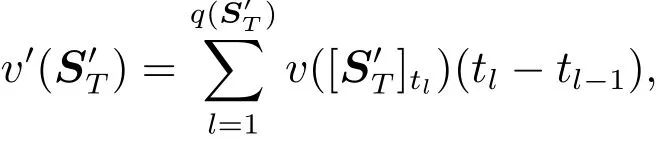
從定義5看,清晰聯盟合作對策v與關于v基于Choquet積分的模糊聯盟合作對策v′之間存在一一對應關系,而且如果v∈G(N)是單調、連續且凸的,則對應的v′也是單調、連續且凸的[9].

4　基于Choquet積分的模糊聯盟合作對策τ值的計算方法

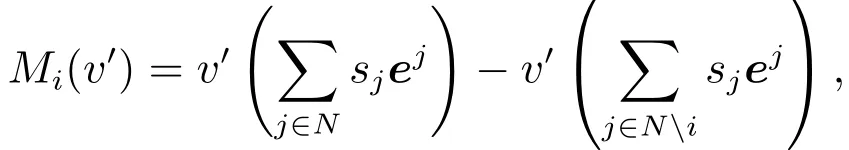
Mi(v′)是局中人i在模糊聯盟中所能獲取的理想支付.如果局中人i想從模糊聯盟中獲得更多支付,則其他局中人會將其驅逐出模糊聯盟.所以,Mi(v′)是局中人i在模糊聯盟合作對策v′中所能獲得支付的上界. M(v′)=(M1(v′),M2(v′),...,Mn(v′))∈Rn稱為模糊聯盟合作對策v′的上值向量.根據定義5,有

令T?N且i∈T.模糊聯盟S′T中局中人i的剩余支付R(S′T,i)可表示為

R(S′T,i)表示模糊聯盟S′T中除局中人i之外其他局中人都獲得可期望得到的最大支付時,局中人i所能得到的剩余支付.模糊聯盟合作對策v′下值向量m(v′)的第i個分量mi(v′)可表示為

它可看作是局中人i的最小合理支付,表示在模糊聯盟S′T中其他局中人獲取到各自理想支付的同時,局中人i可以獲取到盡可能多的剩余支付.

定義6設v′∈Gc(N).對任意則稱v′是擬均衡模糊聯盟合作對策.

用Gfqb(N)表示擬均衡模糊聯盟合作對策的集合.注意當si只取1時,擬均衡模糊聯盟合作對策v′退化成擬均衡合作對策v.

定理1若v∈Gcov(N),則其對應的v′∈Gc(N)有v′∈Gfqb(N).

證明由于v∈Gcov(N),關于v基于Choquet積分的模糊聯盟合作對策v′∈FGcov(N),則v′是均衡的[15].于是,對任意S′N∈Fn,至少存在一組向量x滿足且對任意T?N有因此,對任意i∈N,有

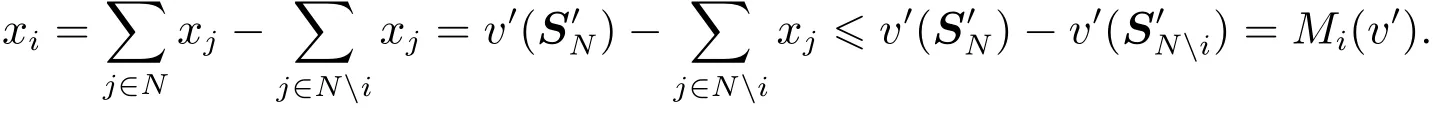
考慮上述關系,對任意T?N且i∈T,有

定義7設v′∈Gc(N)和給定.如果函數fgv′:Fn→R,滿足對任意T?N,有

則稱fgv′為基于Choquet積分的模糊聯盟合作對策v′的分歧函數.

定義8設v′∈Gc(N)和給定.如果向量λv′∈Rn的每一個分量滿足

則稱λv′為基于Choquet積分的模糊聯盟合作對策v′的特許向量.

定理2若v∈Gcov(N),給定,其對應的v′∈Gc(N),滿足對任意i∈N,有

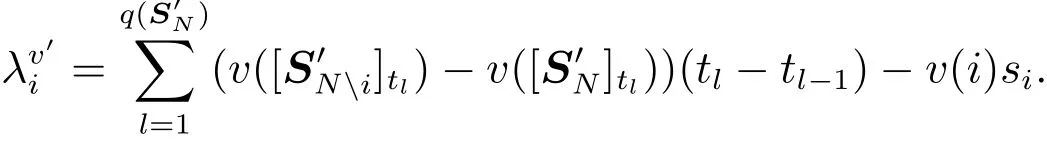
證明因v∈Gcov(N),則有v′∈FGcov(N).對任意T?Ni,根據定義3有

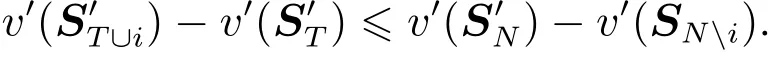
根據定義7,有fgv′(S′T)≤fgv′(S′T∪i),因此對任意T?N且i∈T,有

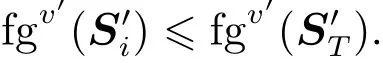
根據定義8,有

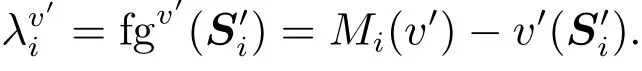
定義9設v′∈Gfqb(N),給定,則

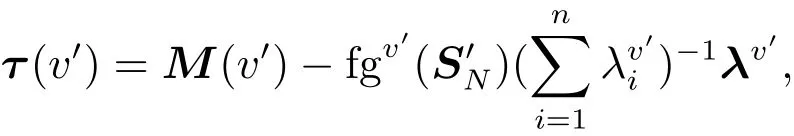
稱τ(v′)為基于Choquet積分的模糊聯盟合作對策τ值.

證明因為v∈Gcov(N),根據定理1,有v′∈Gfqb.依據定義9,對任意i∈N有

又根據定理2,則任意i∈N有

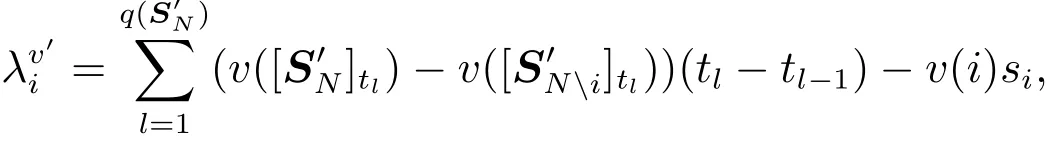
則對任意i∈N有

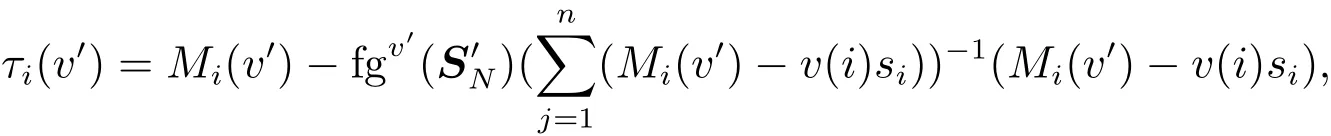
定理3利用凸模糊聯盟合作對策的特點直接計算出特許向量,無需進行多次計算和比較,因此為計算凸模糊聯盟合作對策τ值提供了簡便的方法.

下面給出基于Choquet積分的模糊聯盟合作對策τ值的計算步驟:

步驟1 判斷基于Choquet積分的模糊聯盟合作對策是否是凸的.若是凸的,則進入步驟2;若不是凸的,則進入步驟3.

步驟2根據定理3的τ值計算公式進行計算.

步驟3根據定義6,判斷基于Choquet積分的模糊聯盟合作對策是否滿足擬均衡條件.

步驟4若該對策滿足擬均衡條件,則根據定義9的τ值計算公式進行計算.

下面用一個算例來說明基于Choquet積分的模糊聯盟合作對策τ值的計算過程.

設N={1,2,3}和v∈G(N).其中v(i)=0(任意i∈N),v({1,2})=v({1,3})=2,v({2,3})=3, v({1,2,3})=4.當時,基于Choquet積分的模糊聯盟合作對策τ值計算過程如下:

2)判斷v′是否滿足擬均衡性.根據Mi(v′)的定義,得

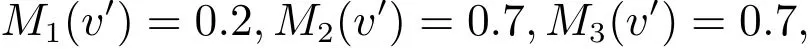
根據mi(v′)的定義,得

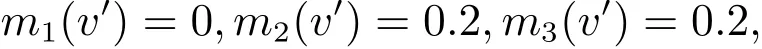
3)計算τ值.根據定義8,得

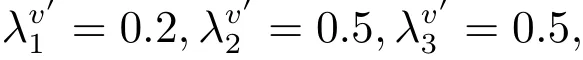
根據定義9,得

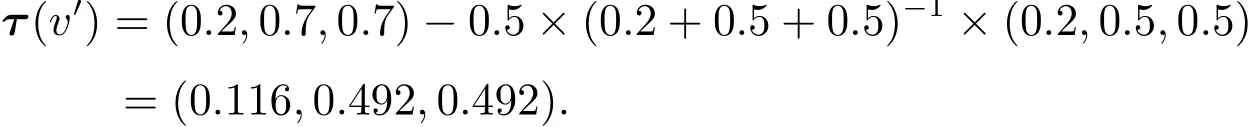
5　基于Choquet積分的模糊聯盟合作對策τ值的性質

定理4基于Choquet積分的模糊聯盟合作對策τ值滿足有效性、個體合理性、對稱性、啞元性、替換性、策略等價下的共變性、限制成比例性等性質.

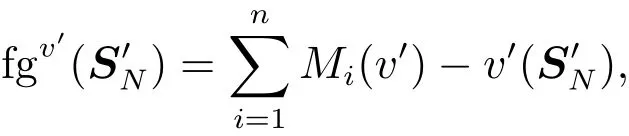
2)因v′∈Gfqb(N),由定義6可知,有.根據fgv′和λv′的定義,有

5)對于任意i,j∈N與T?N{i,j},若v′(S′T∪i)=v′(S′T∪j),則

根據定義7,對任意T?N,有

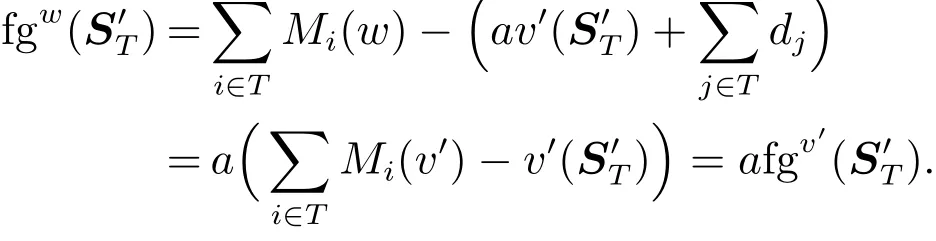
7)限制成比例的證明顯然.證畢.

需要注意的是,當si只取1時,模糊聯盟就退化為清晰聯盟,相應的基于Choquet積分的模糊聯盟合作對策v′就退化為清晰合作聯盟對策v.對應的基于Choquet積分的模糊聯盟合作對策τ值退化成清晰聯盟合作對策τ值,其滿足的性質對應地退化成清晰聯盟合作對策τ值滿足的性質.顯然,基于Choquet積分的模糊聯盟合作對策τ值是對清晰聯盟合作對策τ值的擴展,清晰聯盟合作對策τ值是基于Choquet積分的模糊聯盟合作對策τ值的特例.

定理5基于Choquet積分模糊聯盟合作對策的解如果滿足有效性、策略等價下的共變性和限制成比例性,則這個解是唯一的且這個解就是τ值.

證明必要性.由定理4可知,基于Choquet積分的模糊聯盟合作對策τ值滿足有效性、策略等價下的共變性和限制成比例性.

充分性.假設存在一個解φ滿足以上三個性質,則只需證明φ(v′)=τ(v′)即可.令v′∈Gc(N),定義向量d=M(v′)-λv′和合作對策w∈Gc(N)滿足:對任意T?N,有

由于φ和τ均具有策略等價下的共變性,因此

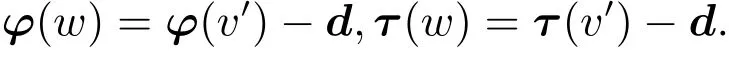
為了證明φ(v′)=τ(v′),只需證明φ(w)=τ(w).

由于對任意i∈N,有

又有

則

又由于φ和τ均具有限制成比例性,則φ(w)與τ(w)均和M(w)成正比.因此存在實數α和β使得

定義10設v′∈Gc(N)和.v′的模糊核心可表示為

模糊核心是所有局中人都能接受的分配方案組成的集合,這是因為任意模糊子聯盟中所有局中人所獲得的支付之和都不少于其聯盟所得的支付.

定理6設v′∈Gfqb(N)和,且滿足的條件為

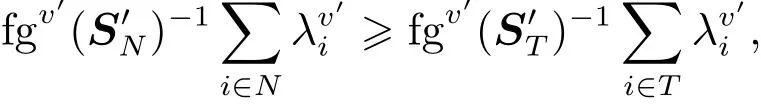
其中T?N,fgv′(S′T)＞0且2≤|T|≤n-2.

證明令x=τ(v′),根據τ值的定義和有效性可知,對任意i∈N,有Mi(v′)-λv′i≤ xi≤ Mi(v′) 且.則有

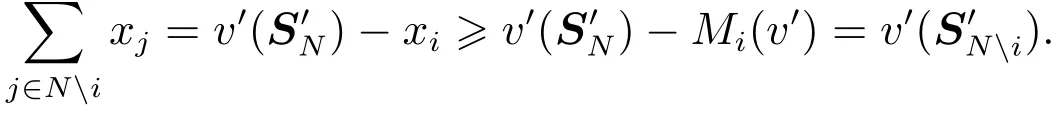
6　案例分析

假設有A、B、C、D、E五家企業集合為N={1,2,3,4,5},他們完全參與到一個生產合作項目當中.若五家企業單獨工作,當i∈{1,2,3,4}時,v(i)=10,而v(5)=20;當|S|=2且S?{1,2,3,4}時,v(S)=30,其他v(S)=50;當|S|=3且S?{1,2,3,4},v(S)=80,其他v(S)=100;當|S|=4且5∈S時,v(S)=200,其他v(S)=150;v(N)=320.根據定義1與2計算出經典清晰聯盟合作對策τ值,如表1所示.

表1　清晰聯盟合作對策的特許值、上值和τ值Table 1 The concession values,the upper values and τ-values of the crisp cooperative game

若生產合作項目中A、D企業只投入其50%企業資源,而B、C和E企業分別投入其40%、30%和20%的企業資源,這樣A、B、C、D、E五家企業在該合作項目中的參與度分別是50%、40%、30%、50%和20%,即s1=0.5,s2=0.4,s3=0.3,s4=0.5,s5=0.2,可表示為模糊聯盟S′N=(0.5,0.4,0.3,0.5,0.2).很顯然,這里描述的清晰聯盟合作對策v是凸的,其基于Choquet積分的模糊聯盟合作對策v′也是凸的.因此,根據定理2和定理3,計算τ值只需利用定義5計算以下部分模糊聯盟形式下的支付值,如表2所示.

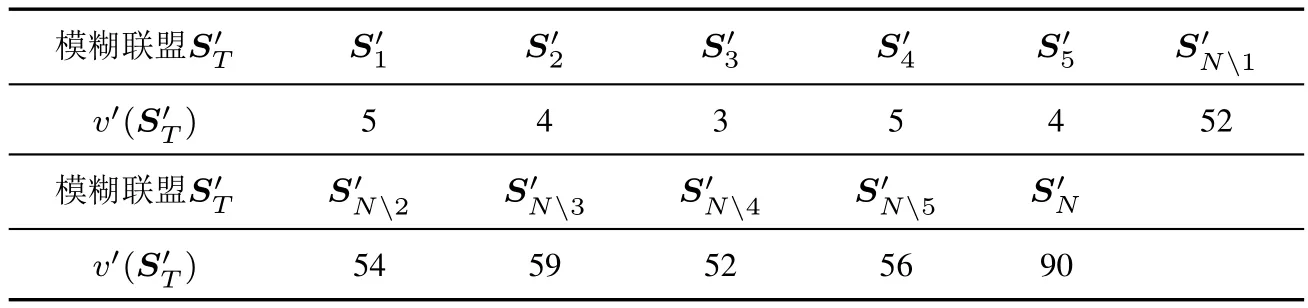
表2　部分模糊聯盟形式下的支付值Table 2 The payoffs of some fuzzy coalitions

根據定理2、定理3及定義8,可以計算出相應的分配方案,計算結果如表3所示.

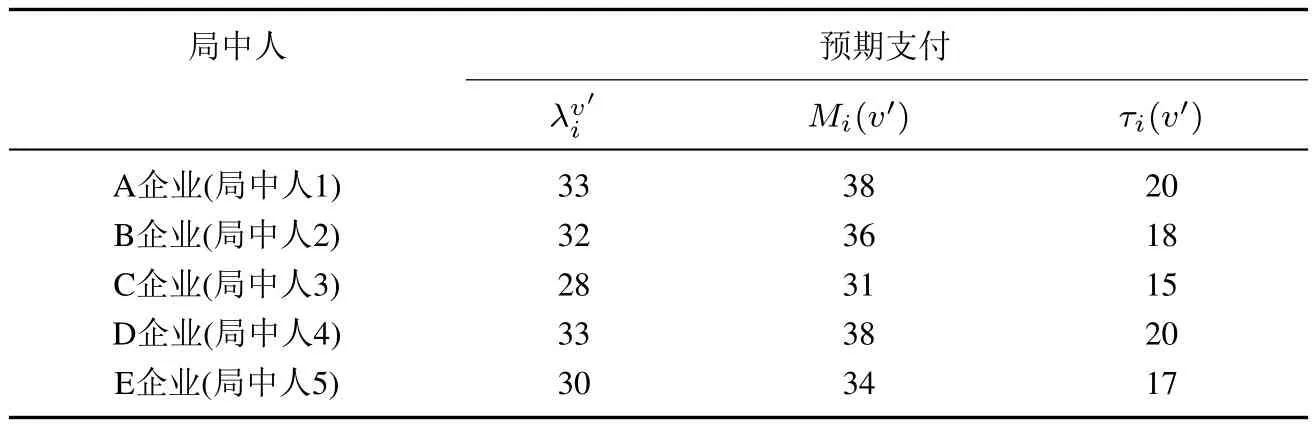
表3　模糊聯盟中各局中人的特許值、上值和τ值Table 3　The concession values,the upper values and τ-values of the fuzzy cooperative game

計算結果為τ(v′)=(20,18,15,20,17).顯然,滿足有效性,且τ1(v′)≥v′(S′1)說明企業1通過合作生產分配得到的支付大于其單干獲得的支付.類似,當i∈{2,3,4,5}時,有τi(v′)≥v′(S′i),所以分配結果也滿足個體合理性.同時,對任意T?N,滿足,所以τ值分配方案滿足模糊核心條件.由于該算例描述的合作對策問題滿足凸模糊聯盟合作對策的條件,對λv′計算可利用定理3的公式,無需對fgv′(S′T)進行計算比較,從而簡化了τ值計算.

按照以上計算過程,可以計算任意模糊聯盟情況下的合作對策τ值,表4是一組不同模糊聯盟情況下的合作對策τ值.

表4　不同模糊聯盟情況下的τ值Table 4　The τ-values of different fuzzy coalitions

7　結束語

本文利用Choquet積分方法對清晰合作對策進行模糊拓展,在此基礎上提出基于Choquet積分的模糊聯盟合作對策的τ值.該τ值具有個體合理性、對稱性、啞元性等性質,且是模糊聯盟合作對策滿足有效性、策略等價下的共變性和限制成比例性的唯一解.研究發現,基于Choquet積分的模糊聯盟合作對策的τ值是經典合作對策τ值的模糊拓展,經典合作對策τ值是其特殊情況.同時,若基于Choquet積分的模糊聯盟合作對策是凸的,則其τ值存在且其特許向量和τ值計算公式可以簡化,從而提高了其計算效率.算例說明,利用基于Choquet積分的模糊聯盟合作對策的τ值可在局中人以不同參與度參加合作時計算出一種合理的分配方案,可作為合作談判中的重要參考信息.但該τ值的使用需要滿足一定的條件,比如,利用Choquet積分方法構造模糊聯盟的支付函數要求聯盟局中人的資源是可拆分量化且可組合產生支付;該τ值的存在性取決于模糊聯盟合作對策是否滿足擬均衡模糊聯盟合作對策條件等.另外,本文僅研究模糊聯盟合作對策τ值的定義和求解,但現實中,局中人常以多層聯盟結構形式參與合作,今后研究重點將考慮具有模糊聯盟結構的合作對策解的定義和求解方法.

[1]Shapley L.A value forn-person games//Kuhn A,Tucker A.Contributions to the Theory of Games.Princeton:Princeton University Press,1953:307–317.

[2]Owen G.Characterization of the Banzhaf-coleman index.SIAM Journal on Applied Mathematics,1978,35(2):315–327.

[3]Tijs S.Bounds for the core and theτ-value//Moeschlin O,Pallaschke D.Game Theory and Mathematical Economics.North-Holland: Amsterdam,1981:123–132.

[4]Driessen T.Cooperation Games,Solutions and Applications.Netherlands:Kluwer Academic Publisher,1988.

[5]Bilbao J,Jiménez-losada A,Lebrón E,et al.Theτ-value for games on matroids.Top,2002,10(1):67–81.

[6]Casas-mendez B,Garcia-jurado I,Nouweland A,et al.An extension of theτ-value to games with coalition structures.European Journal of Operational Research,2003,148(3):494–513.

[7]安世虎.準擬陣合作對策的τ值.系統工程理論與實踐,2012,32(1):139–145. An S H.τ-value for strictly cooperative games on matroids.Systems Engineering:Theory and Pratice,2012,32(1):139–145.(in Chinese)

[8]侯東爽,孫浩.廣義特征函數下合作對策的τ值.應用數學學報,2008,31(2):324–332. Hou D S,Sun H.Theτvalue of cooperative games with generalized characteristic functions.Acta Mathematicae Applicatae Sinica, 2008,31(2):324–332.(in Chinese)

[9]Tsurumi M,Tanino T,Inuiguchi M.A Shapley function on a class of cooperative fuzzy games.European Journal of Operational Research,2001,129(3):596–618.

[10]譚春橋,陳曉紅.基于Choquet積分的n人對策模糊延拓方法的研究.系統工程學報,2009,24(4):479–483. Tan C Q,Chen X H.Fuzzy extension ofn-persons games based on Choquet integral.Journal of Systems Engineering,2009,24(4): 479–483.(in Chinese)

[11]譚春橋.基于Choquet積分n人對策廣義模糊延拓方法.系統工程學報,2012,27(2):193–200. Tan C Q.Generalized fuzzy extension ofn-persons games based on Choquet integral.Journal of Systems Engineering,2012,27(2): 193–200.(in Chinese)

[12]譚春橋.基于Choquet延拓具有區間模糊聯盟n人對策的Shapley值.系統工程學報,2010,25(4):451–458. Tan C Q.Shapley value forn-persons games with interval fuzzy coalition based on Choquet extension.Journal of Systems Engineering,2010,25(4):451–458.(in Chinese)

[13]Li S J,Zhang Q.A reduced expression of the Shapley function for fuzzy game.European Journal of Operational Research,2009, 196(1):234–245.

[14]孟凡永,張強,孫紅霞.模糊合作對策上的Banzhaf函數.系統工程學報,2012,27(1):1–8. Meng F Y,Zhang Q,Sun H X.Banzhaf function on function on fuzzy cooperative games.Journal of Systems Engineering,2012, 27(1):1–8.(in Chinese)

[15]Shapley L.Cores of convex games.International Journal of Game Theory,1971,1(1):11–26.

τ-values of cooperative games with fuzzy coalitions and solving method

Yang Dianqing,Li Dengfeng*
(School of Economics and Management,Fuzhou University,Fuzhou 350108,China)

Considering fuzzy coalitions appearing in the practical cooperation,this paper defines the τ-value for the fuzzy cooperative game with Choquet integral,and proves its existence,uniqueness and some important properties.The relation between the τ-value and the fuzzy core is discussed.The computational formula of τ-value for the convex fuzzy cooperative game is given.Finally,the effectiveness and rationality of the τ-value is illustrated by a numerical example.The result shows that the τ-value for the fuzzy cooperative game with Choquet integral is an extension of the τ-value for crisp cooperative game.Especially,for the convex fuzzy cooperative game,the computational process of the τ-value can be simplified.

fuzzy cooperative game;Choquet integral;τ-value;game theory;fuzzy set

O225

A

1000-5781(2016)01-0013-11

10.13383/j.cnki.jse.2016.01.002

2014-03-28;

2015-02-05.

國家自然科學基金重點資助項目(71231003);國家自然科學基金資助項目(71171055);高等學校博士學科點專項科研基金資助項目(20113514110009);國家教育部新世紀優秀人才支持計劃資助項目(NCET-10-0020);福建省社會科學規劃資助項目(2012C022).

.

楊靛青(1979—),男,福建漳州人,博士生,講師,研究方向:模糊決策與對策,Email:52881164@qq.com;

李登峰(1965—),男,廣西博白人,教授,博士生導師,研究方向:經濟管理決策與對策、運籌管理與模糊系統分析等,Email: lidengfeng@fzu.edu.cn.