風險規避供應鏈的最優兩部定價契約

代建生

(昆明理工大學管理與經濟學院,云南昆明650093)

風險規避供應鏈的最優兩部定價契約

代建生

(昆明理工大學管理與經濟學院,云南昆明650093)

在雙邊道德風險下,研究了制造商和銷售商均風險規避且都具有一定談判能力下的最優兩部定價契約.發展了一種方法來求解最優契約參數,并考察了渠道成員的風險規避、談判能力和保留效用,以及市場需求波動等外生變量對契約參數的影響,研究表明:最優批發價格隨制造商風險規避程度增大而下降,隨銷售商風險規避程度增大而上升.刻畫了市場需求波動影響最優批發價格的臨界條件.最后利用數值算例驗證了結論的有效性.

供應鏈管理;兩部定價;風險規避;納什談判;雙邊道德風險

1　引　言

兩部定價由線性分成比例(在供應鏈合約實踐中常以批發價格形式出現)和固定轉移支付組成.通過兩部定價機制,渠道成員可得到供應鏈縱向整合的最優結果并實現利潤在參與者之間的任意分配.兩部定價契約具有許多優點,相對于單一價格契約,兩部定價契約更有效率[1-2];相對于數量折扣契約,在一定條件下,兩部定價契約對制造商更為有利[3].這一契約機制在供應鏈合約實踐中被廣泛采用,比如,在連鎖經營模式中,加盟商除了按批發價格向總部訂購商品外,還向連鎖總部支付加盟費和(或)管理費用,這些費用是加盟店給予連鎖總部的單邊轉移支付;一般品牌制造商欲進入沃爾瑪或家樂福等零售巨頭的銷售渠道時,除了按批發價向零售巨頭供給商品外,通常要繳納進場費、贊助費、場地使用費等多種費用,這些費用在本質上是制造商向銷售商的單邊轉移支付.

對兩部定價契約已進行了大量的研究,其中一簇重要的文獻關注于如何設計最優契約來改善系統的運行效率[4-7].Giannoccaro和Pontrandolfo[4]針對渠道合作中的機會主義行為,討論了如何設計最優兩部線性契約來激勵成員加大投入,促進渠道協作.Jeuland和Shugan[5]從制造商的角度考察了如何通過兩部定價機制實現供應鏈縱向整合的最優結果.劉京軍和梁建峰[6]考慮離散投資環境中,基金投資委托人如何運用最優線性契約來激勵管理人.于麗萍等[7]考察了制造商以提供商業信用、零售商以廣告形式進行合作的最優兩部定價契約設計.

上述文獻是在無道德風險或單邊道德風險背景下對兩部定價契約進行的研究.事實上,無論是制造商還是銷售商,由于彼此信息的不對稱,都有搭便車的激勵,因而存在雙邊道德風險問題.一些文獻在這一背景下對兩部定價契約進行了研究[8-12],得到一個基本結論:在雙邊道德風險下,兩部定價契約通常不能實現系統的帕累托最優.這些文獻假定合作一方毫無談判能力,這很具限制性.比如,當電器銷售巨頭國美或蘇寧面對電器生產巨頭海爾或長虹時,任何一方都不可能擁有完全的談判能力,以至于可以提供一個要么接受要么拒絕的合約供另一方選擇.張欽紅和駱建文[13]以及孟衛東等[14]在渠道雙方都具有一定談判能力且存在雙邊道德風險的假定下探討了供應鏈的激勵和協調問題.

前面有關雙邊道德風險的文獻假定渠道成員風險中性,在這種情形下,只要市場需求的期望值不變,其波動大小對渠道成員的效用及策略選擇就沒有影響,因而最優契約參數與市場需求波動大小無關,但這與現實觀察是不符的.事實上,決策者的行為往往表現出某種風險規避的特性[15-16].直覺上,如果渠道成員風險規避,即使市場需求期望保持不變,只要需求波動大小發生變化,既定契約安排下渠道成員的效用必然發生改變,因而渠道成員有改變策略選擇的激勵,這意昧著供應鏈的最優契約在不同需求波動下是不同的.已有研究指出:相對于風險中性者,風險規避者的行為更保守,因而市場需求不確定對契約設計有重要影響[17-19].渠道成員的風險規避對兩部定價契約有何影響呢?本文力圖回答這一問題.

本文在雙邊道德風險下考察渠道成員風險規避、市場需求波動和相對談判能力對最優兩部定價契約的影響.技術上,使用指數效用函數來描述渠道成員的風險偏好,這一效用函數在金融和運營等管理文獻中得到廣泛運用[6,19-22],同時使用納什談判解來討論渠道利益的分配和談判問題,這一方法在經濟和運營文獻應用較為普遍[13,14,19,23,24].與本文最相關的研究是孟衛東等[14],他們在雙邊道德風險下考察了渠道成員通過納什討價還價確定利益分配下的兩部定價契約設計問題,但他們假定渠道成員是風險中性的,本文討論的是渠道成員風險規避的情形.Gan等[19]與本文的研究也是相關的,他們運用指數效用函數和納什談判解,考察了風險規避供應鏈的協調和談判問題,但他們沒有考慮渠道促銷問題,也不關注兩部定價契約.

2　渠道合作模型

制造商和銷售商進行渠道合作,制造商負責產品的生產,銷售商負責產品的銷售.為了簡化分析,本文僅考察市場價格外生給定下的利益分配問題.不失一般性,將商品價格與單位生產成本的差設為1.商品實現的收益只依賴于商品銷量,商品銷量與質量改進和促銷力度有關,同時受到不確定因素的影響.商品的質量改進由制造商負責,并由其投入水平e1確定;而促銷由銷售商負責,促銷力度由銷售商的投入水平e2來刻畫(在本文中,用下標1來指代制造商,下標2指代銷售商).商品銷量Y是雙方投入水平的函數

其中ei∈[0,∞),函數f的Hesse陣處處負定且;隨機變量ε～N(0,σ2),其中σ2反映了市場需求的波動大小.

為了實現渠道協作,渠道雙方通過談判達成以下分成契約:渠道成員i所得收入為Yi=ti+wiY,其中t1+t2=0,w1+w2=1且wi≥0.wi為線性分成比例,ti為固定轉移支付,可正可負.

質量改進或促銷過程中產生的成本記為ci(ei),它關于ei二階可導且嚴格凸增.成員i從渠道合作中實現的利潤為Yi-ci(ei).渠道成員具有不變的絕對風險偏好(CARA),其效用函數為

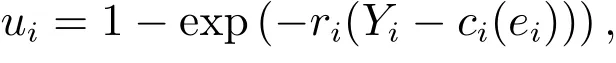
其中ri＞0為成員i的絕對風險規避系數.注意到ε～N(0,σ2),渠道成員i的期望效用可表述為

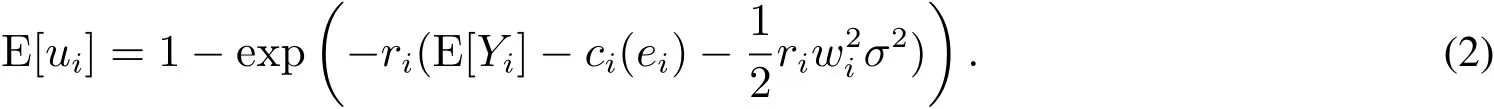
令r12=r1/r2,它表示渠道成員的相對風險規避程度:r12＞1表示制造商更加風險規避,r12＜1表示銷售商更加風險規避.

渠道成員擁有參與或不參與渠道協作的自由,成員i的保留效用設為u0i.質量改進和促銷的投入不可相互觀察,或者可觀察但不能被第三方所證實,因而存在雙邊道德風險.給定契約安排,渠道成員總是選擇能使自身效用最大化的投入水平.渠道雙方通過談判確定渠道收益的分配,設τi為成員i的談判力因子,滿足0≤τi≤1且τ1+τ2=1.合作雙方按納什談判解分享合作剩余,并選擇保留效用作為談判威脅點,技術上要求納什積函數最大化.綜上,供應鏈面臨以下問題(P1)[25]

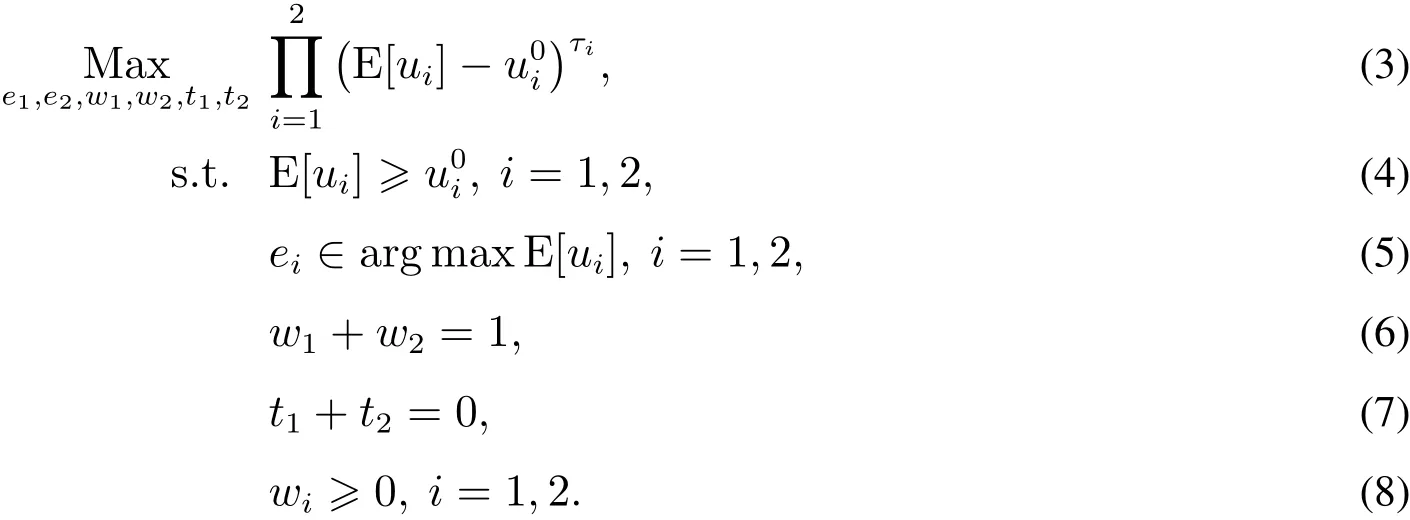
式(3)表示供應鏈選取最優兩部定價契約和投入組合以最大化納什積函數.式(4)為IR約束,成員參與渠道協作所得期望效用不小于各自的保留效用,否則它將退出渠道協作.特別地,由于渠道成員擁有參與自由,所有渠道成員的個體理性約束都必須得到滿足.式(5)為IC約束,由于行動的不可觀察,合作各方追求自身期望效用的最大化.式(6)和式(7)為BB約束,合作剩余完全在合作雙方之間進行分配.式(8)為非負約束,它是對利益份額取值為正的規定,這一限定與兩部定價契約實踐是相符的.

3　模型分析

3.1最優線性分配比例

式(5)的一階最優條件為

用式(9)替代式(5),將相應的規劃記為P2.特別地,P1與P2有同解,因為E[ui]關于ei是嚴格凹的,IC約束的一階必要條件也是充分條件[26].

命題1P2的解也是P3的解.

根據命題2,要求解P2,總可先求解P3,找出解的前四個分量,再根據P2目標函數極大化的要求求解后兩個分量.下面來求解P3.為了推導的方便,令F(e1,e2,w1,w2)=(F1(e1,e2,w1,w2),F2(e1,e2,w1,w2)),其中.由式(9),有

其中0表示分量為0的二維行矢量.

對F(e1,e2,w1,w2)求關于e1和e2的一階偏導數,有

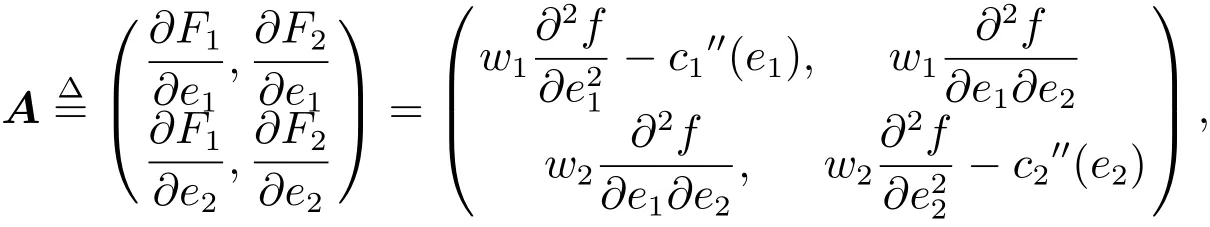
由成本函數的凸性和生產函數f的Hesse陣的負定性,矩陣A的行列式|A|≥0.特別地,當f嚴格負定或成本函數嚴格凸時,|A|＞0,則A-1存在,后文總是在這一假定下進行討論.這一設定并不具有很大的限制性,它包括了文獻中經常使用的兩類函數族:①f是線性的,但ci(ei)是嚴格凸的,如;②f是嚴格凹的,但ci(ei)是線性的.

方程(10)隱含地確定了e1與e2關于w1和w2的函數關系

根據隱函數定理,有

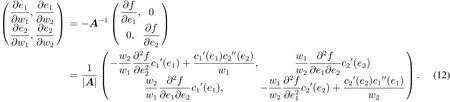
將式(11)代入P3的目標函數,將其簡記為W(w1,w2).求解P3,先不考慮IR約束(事后進行檢驗),如此,約束式(7)將變得無關緊要(命題2);且根據式(9),有wi＞0,故非負約束式(8)得到滿足.綜上,P3簡化為在約束式(6)下極大化W(w1,w2),其關于w1和w2的一階最優條件為

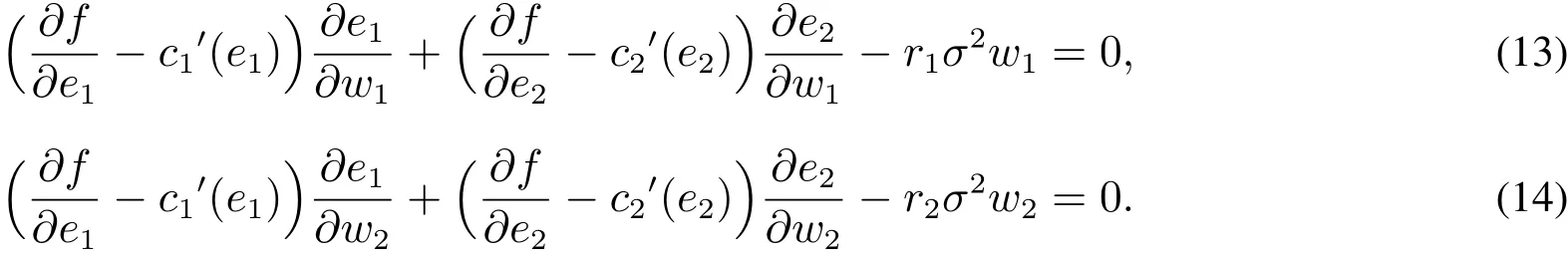
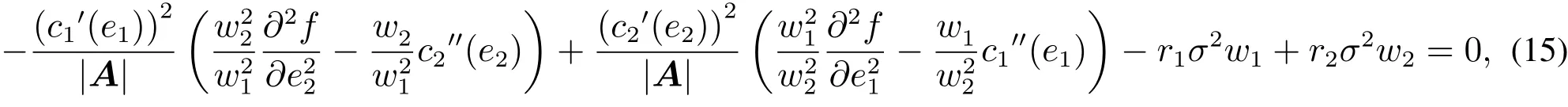
將式(9)和式(12)代入式(13)和式(14),并利用式(6),有式(15)和式(6)隱含地確定了wi與參數r1、r2和σ2的函數關系.令wi=w*i滿足式(6)和式(15),借助式(9)可解出e*i.因式(15)不含變量τ1和τ2,故在P1、P2和P3的解中,(e*i,w*i)與談判力因子無關.孟衛東等[14]在風險中性假設下指出最優線性分配比例與談判能力無關.根據前面的討論,這一結論在風險規避假設下仍然成立.

定理1.在渠道協作中,1)當市場需求確定時,最優線性分配比例與渠道成員的風險規避程度無關.2)當市場需求波動時,一方所得線性分配比例隨自身風險規避程度增加而減小,隨對方風險規避程度增加而增大;市場需求波動對分配比例的影響依賴于雙方相對風險規避程度的大小:當rjw*j＞riw*i時,渠道成員i所得最優線性分配比例隨市場需求波動的增大而上升;當rjw*j＜riw*i時,渠道成員i所得最優線性分配比例隨市場需求波動的增大而下降.

證明1)由式(15)可知,當σ2=0時,wi與風險規避系數r1和r2無關,即當市場需求確定時,(e*i,w*i)與雙方的風險規避程度無關.

2)P3的目標函數可視為w1與r1、r1和σ2的函數,不妨將P3的目標函數重新表述成

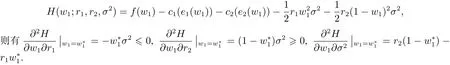
由Topkis[27]的定理3.2和Amir[28]的引理1,在P3的目標函數H(w1;r1,r2,σ2)中,內生變量w1與外生變量r1是子模的,變量w1與r2是超模的;當rjwj＞riwi時,w1與σ2是超模的,否則是子模的.由Topkis[27]的定理6.1和Amir[28]的定理9,有,當rjw*j＞riw*i時,;當rjw*j＜riw*i時,. P3的目標函數也可表示為H(w2;r1,r2,σ2),上面的討論同樣適用.證畢.

當市場需求確定時,最優線性分配比例與渠道成員風險規避程度無關,這一結論是顯然的.當市場需求波動時,一方所得線性分配比例隨自身風險規避程度增加而減小,隨對方風險規避程度增加而增大,這一結論也是符合直覺的,因為在兩部定價契約中,固定轉移支付部分相當于確定性資產,而與線性分配比例相對應的收益是風險性資產.當某一渠道成員變得更為風險規避時,通過減少其風險性資產在資產組合中的配比,能改善整個系統的效率.市場需求波動對線性分配比例的影響更為復雜,不能依靠直覺得到,定理1刻畫了市場需求波動如何影響最優線性分配比例的臨界條件.

前文將市場價格與單位生產成本的差模型化為1,因而制造商的線性分成比例w1可解釋為批發價格(兩者至多相差一個常數項).定理1提供了以下管理洞見,第一、當渠道一方變得更加厭惡風險時(如經歷某一災害而遭受了重大經濟損失),有必要調整批發價格:如果制造商變得更加規避風險,批發價格應調減,反之,如果銷售商變得更加規避風險,則應提高批發價格.第二、如果現有批發價格滿足條件,當市場需求波動更大時,應提高批發價格,否則降低批發價格;如果,則執行相反的政策.特別地,如果制造商風險中性而銷售商風險規避,市場需求波動越大,批發價格應越高;如果制造商風險規避而銷售商風險中性,市場需求波動越大,批發價格應越低.

當渠道成員風險中性時,即當r1=r2=0時,式(15)可簡化為

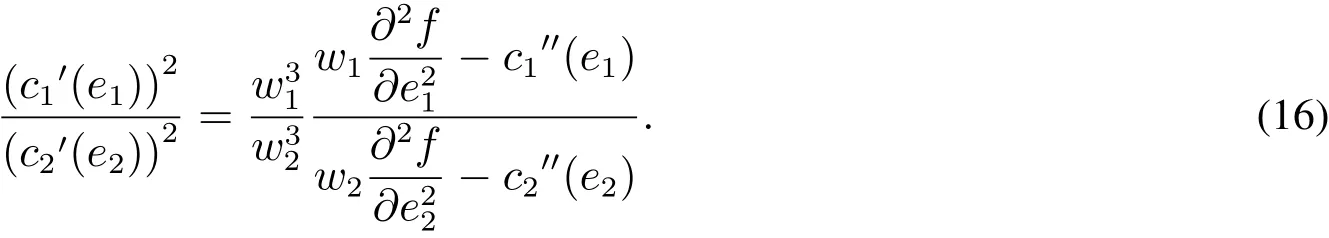
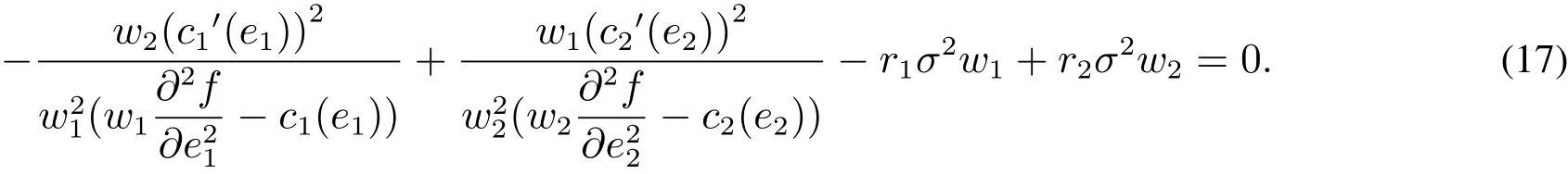
3.2最優固定轉移支付

令u0i=1-exp(-v0i).命題2表明(t*1,t*2)是以下規劃的解(記為P4),即

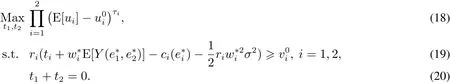
設λi是P4中與IR約束對應的拉格朗日乘子,構造P4的廣義拉格朗日函數

對L求t1和t2的偏導,簡單變形,得到

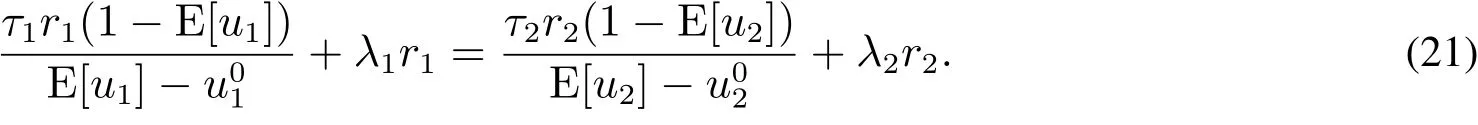
命題3.在P4的解中,當τi=0時,λi＞0;當0＜τi＜1時,λi=0.

當某一渠道成員毫無談判能力時,與之對應的約束是繃緊的,這表明它參與合作所得收益正好等于保留收益,沒能額外分享因合作產生的凈剩余.當渠道合作雙方的談判力均不為零時,雙方都將參與合作凈剩余的分配.

由命題3及式(21),有

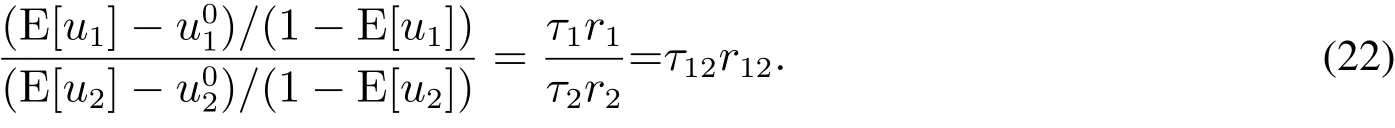
將式(2)代入上式,注意到t1+t2=0,有

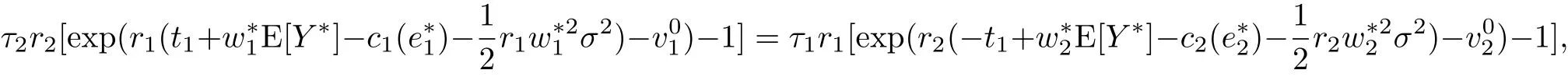
上式隱含地確定了t1與v01、v02、τ1及τ2這四個變量的關系.注意到w*i和e*i與上述四個變量無關,運用隱函數定理,分別求t1關于v01、v02、τ1及τ2的偏導,可得以下結論.

定理2.在渠道協作中,各方所得固定轉移支付隨自身保留效用和談判能力增大而增大,隨對方保留效用和談判能力的增大而減小.

一方保留效用增加,參與渠道協作的機會成本增加,談判基點增大,因而要求增加轉移支付.談判能力增強,要求從合作剩余中分得的收益增加,由于線性分配比例不隨談判能力的變化而變化,因而要求轉移支付增加.在商業實踐中,當制造商(銷售商)擁有新增的銷售(供貨)渠道,可能導致制造商(銷售商)的保留效用增加.因此,供應鏈一方通過加強渠道建設,能獲得對現有渠道伙伴的競爭優勢.渠道成員通過品牌建設,增強經濟實力和談判技巧等,或者獲得專利及獨家經營權,有助于增大該成員在與現有伙伴合作中利益分配的談判能力,從而獲取更大的利益分配份額.

盡管P4的解必然滿足式(22),但滿足式(22)的解未必是P4的解,除非它還滿足約束(19).下面來討論這個問題.在最優線性分配比例下,為了確保渠道成員參與渠道合作而補償給渠道成員的最低支付,稱之為最低轉移支付,如果補償小于這個支付,渠道成員沒有參與的激勵,渠道合作無法達成.將成員i的最低轉移支付記為,它滿足,解之,得

命題4不僅提供了判定P4解存在的充要條件,而且給出了最優固定轉移支付取值的邊界:其下界使自己剛好獲得保留效用,其上界使對方恰好獲得保留效用.

4　數值分析

4.1最優線性分配比例的求解及敏感性分析

上一節給出了最優批發價格和固定轉移支付滿足的方程,但沒有給出兩個變量的顯性解.事實上,方程(22)是一個關于ti的超越方程,沒有解析解.為了進一步驗證理論推導的正確性,以及進行更深入的探討,本小節對上述模型進行數值分析.設某供應鏈由單一的制造商和單一的銷售商組成,制造商負責生產商品并通過銷售商進行銷售.為了取得競爭優勢,制造商投入成本e1改進產品質量,而銷售商投入成本e2來加強市場營銷.商品銷量與渠道投入的函數關系為,其中a1,a2＞0,a1和a2的差異反映了渠道成員的投入對終端市場需求的不同影響.

由式(9),有

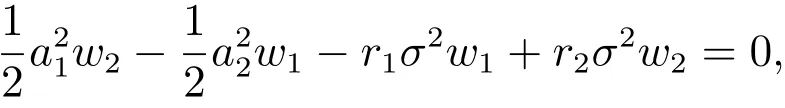
將約束(6)代入上式,解得

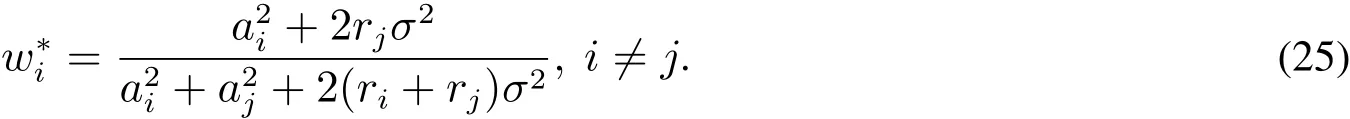
由ri≥0,有wi＞0,這表明非負約束(8)得到滿足.

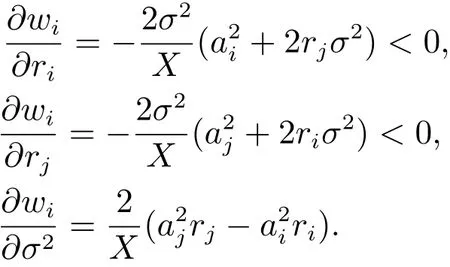
易驗證上面的結果與定理1保持一致.

下面進行數值分析,除非特別說明,后文中的參數值設定為a21=10,a22=15,r1=1,σ2=1,v01= 1,v01=0.5.圖1在四種不同的市場波動情形下繪制了w*1隨r2的變化情況.在隨機需求下,隨著銷售商風險規避程度的增加,制造商相對于銷售商的風險規避程度遞減,批發價格遞增.由于商品收益是不確定的,這表明制造商承擔了更多的風險;在確定需求下,批發價格與相對風險規避程度無關.圖2反映了批發價格隨市場波動程度的變化曲線.當a22r2＞a21r1時,批發價格隨需求波動程度增加而增加;當a22r2＜a21r1時,批發價格隨需求波動程度增加而減小,當a22r2=a21r1時,批發價格維持恒定.四條曲線在σ2=0時交匯于一點,當市場需求確定時,無論渠道成員的風險規避程度如何,最優批發價格保持不變.圖1和圖2都表明,市場需求波動越大,相對風險規避程度對批發價格的影響越大.

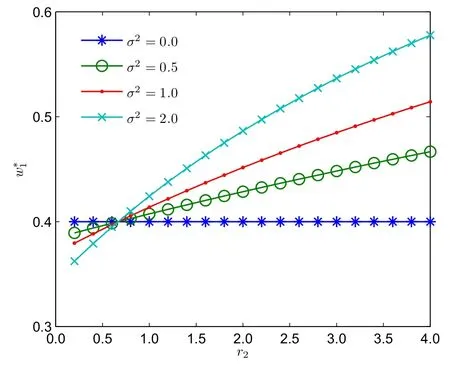
圖1　w*1隨r2的變化曲線Fig.1 The curve line of w*1with respect to r2

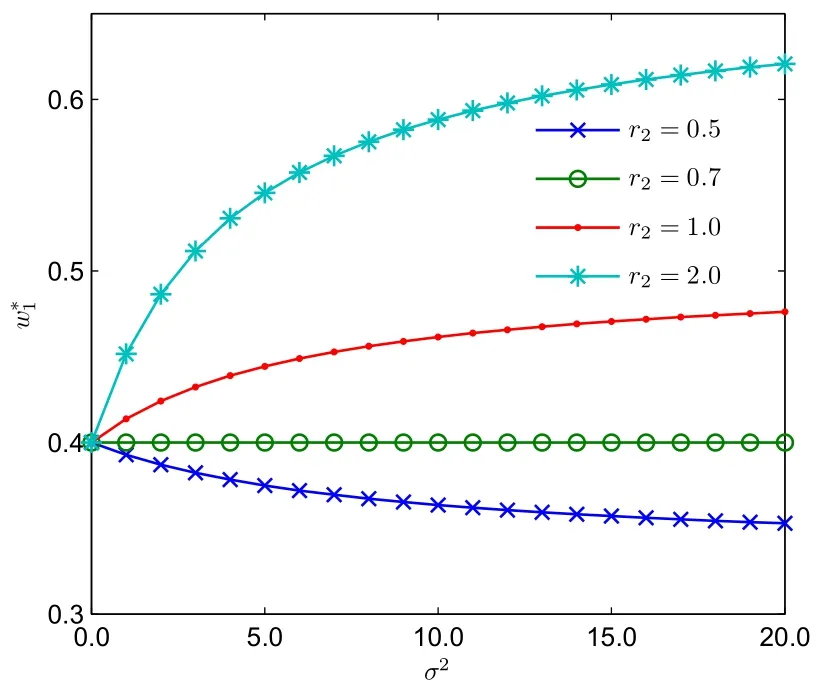
圖2　w*1與σ2的變化曲線Fig.2 The curve line of w*1with respect to σ2

4.2最優轉移支付影響因素分析

當r2=2時,由式(24)和式(25)可解得(e*1,e*2,w*1,w*2)=(0.509 9,1.127 7,0.451 6,0.548 4);運用公式(23)并借助數值算法可解得,由命題4,P4的解存在,且有.可類似計算r2為其它值的最低轉移支付.圖3繪制了t*1隨τ12的變化情況:當τ12→0時,;當τ12→∞時,,其中t*1可正可負:當t*1＞0時,表示銷售商向制造商支付渠道費用,比如加盟商向總部支付的管理費;當t*1＜0時,表示制造商向銷售商支付渠道費用,比如制造商向沃爾碼等零售巨頭繳納的進場費.從圖3可知,當相對談判能力差異極其顯著時,t*1隨τ12的變化趨近于收斂,其下界為,上界為-,其經濟含義是:如果制造商相對于銷售商毫無談判能力,制造商只能獲得保留效用;反過來,當銷售商毫無談判能力時,銷售商只能獲得保留效用.圖4反映了σ2=3的情形,相對于圖3,圖4中t*1的上界和下界都被壓縮,因為當市場波動增大時,風險規避的制造商和銷售商的風險補償增加,在IR約束下,雙方的最低轉移支付都將增大.圖3和圖4聯合表明:當市場需求波動增加時,相對談判能力對固定轉移支付的影響將減弱.

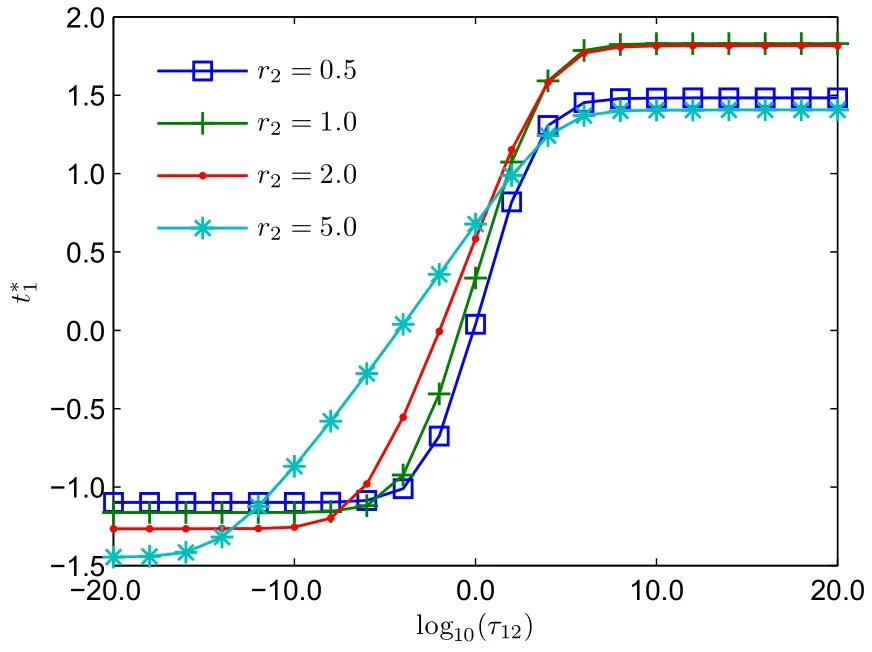
圖3　t*1隨τ12的變化曲線(σ2=1)Fig.3 Effect of τ12on t*1(σ2=1)

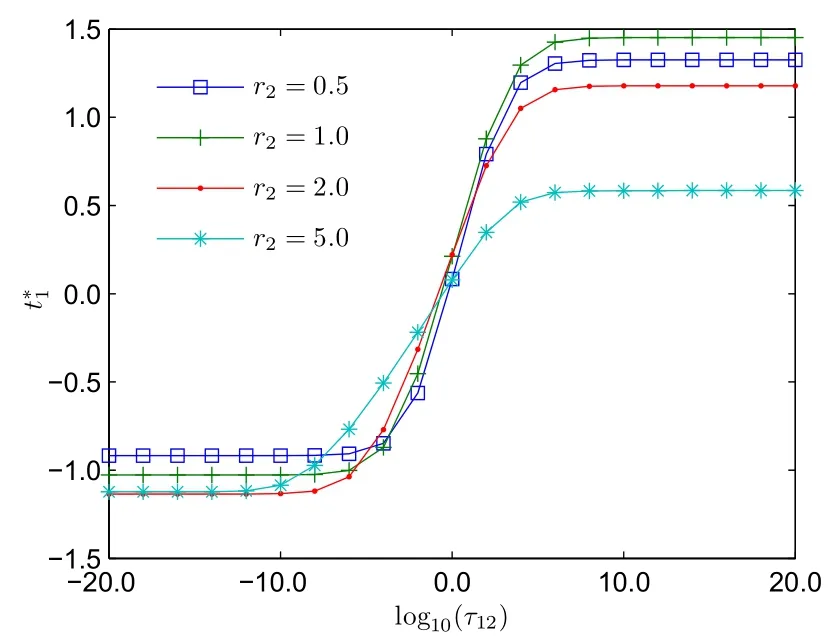
圖4　t*1隨τ12的變化曲線(σ2=3)Fig.4 Effect of τ12on t*1(σ2=3)

給定參數τ12=5,圖5反映了t*1隨v01的變化情況:制造商的轉移支付和保留效用具有正向線性關系.圖6反映了相對風險規避程度與轉移支付的關系:與談判能力和保留效用有所不同,相對風險規避程度對轉移支付的影響較為復雜,不再是單調變化的關系,而是顯著地受到相對談判能力的影響.

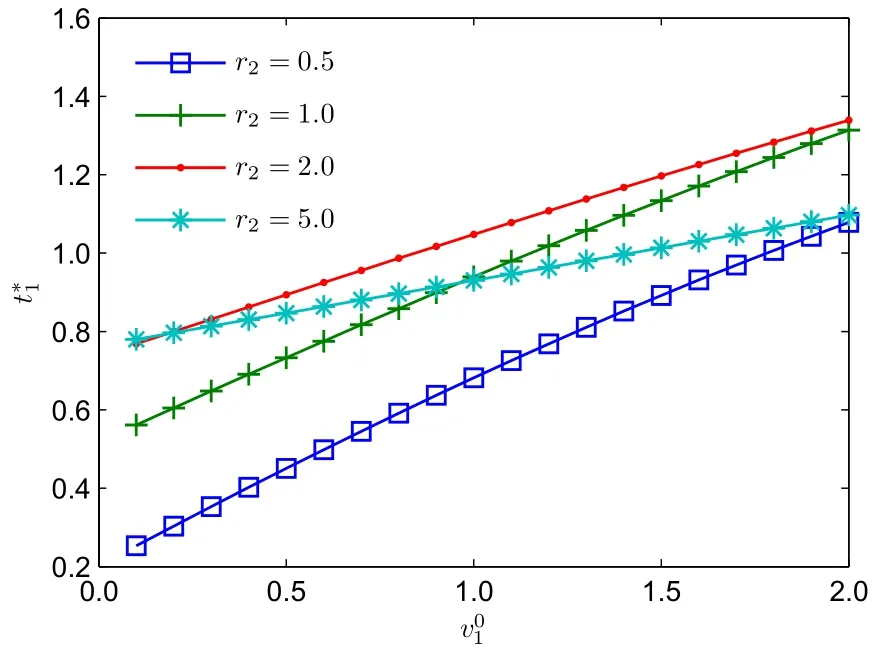
圖5　t*1隨v10的變化曲線Fig.5 Effect of v10on

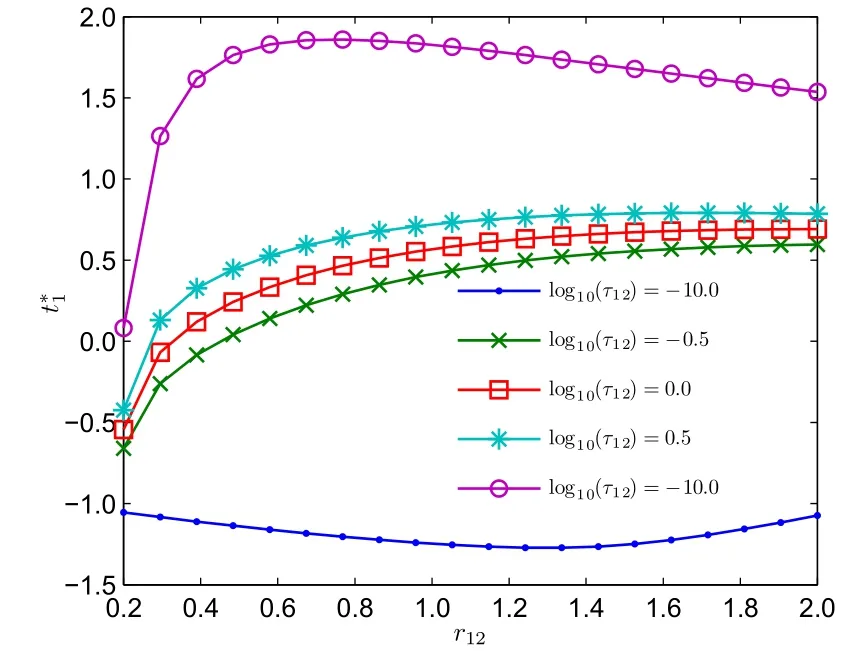
圖6　t*1隨r12的變化曲線Fig.6 Effect of r12on

5　結束語

風險規避供應鏈的最優兩部定價契約受到渠道成員風險規避程度、市場需求波動程度以及相對談判能力等因素的影響.本文發展了一種算法可先求解最優線性分配比例,再確定最優固定轉移支付,從而獲得兩部定價契約的最優解.研究表明,在確定需求下時,制造商與銷售商的風險規避程度對批發價格沒有影響.在隨機需求下,渠道成員風險規避程度對最優批發價格施加重要影響;市場需求波動越大,其影響就越大.兩部定價契約中的單邊轉移支付依賴于渠道成員的保留效用和談判能力,一方的保留效用和談判能力越大,獲取的單邊支付就越大.特別地,無論渠道成員是否風險規避,最優批發價格與談判能力無關.

通過討論,得到以下管理啟示,當制造商變得更加規避風險時,批發價格應調減,反之,當銷售商變得更加規避風險時,則應提高批發價格.如果現有的批發價格滿足條件,當市場需求波動變得更大時,應提高批發價格,否則降低批發價格;如果,則執行相反的政策.通過加強渠道和品牌建設,增強經濟實力和談判能力,能取得對現有渠道伙伴的競爭優勢,從而在渠道協作的利益分配中獲益.

本文的討論是在影響市場需求的隨機變量服從正態分布下進行的,這一假設具有較大的限制性,下一步可在隨機變量服從更一般的分布下對風險規避供應鏈的兩部定價契約進行研究.

[1]石巋然,肖條軍.一類零售商驅動型供應鏈契約問題.系統工程學報,2009,29(6):680–687. ShiKR,XiaoTJ.Contractproblemofthesupplychaindrivenbyretailer.JournalofSystemsEngineering,2009,29(6):680–687.(in Chinese)

[2]Feng Q,Lu L X.Supply chain contracting under competition:bilateral bargaining vs.stackelberg.Production and Operations Management.,2013,22(3):661–675.

[3]Raju J,Zhang Z J.Channel coordination in the presence of a dominant retailer.Marketing Science,2005,24(2):254–262.

[4]Giannoccaro D,Pontrandolfo P.Supply chain coordination by revenue sharing contracts.International Journal of Production Economics,2004,89(8):131–139.

[5]Jeuland A P,Shugan S M.Managing channel profit.Marketing Science,2008,27(1):52–69.

[6]劉京軍,梁建峰.道德風險下的最優委托理財契約研究.系統工程學報,2009,29(5):602–606. Liu J J,Liang J F.Optimal contract for delegated portfolio management with moral hazard.Journal of Systems Engineering,2009,29(5):602–606.(in Chinese)

[7]于麗萍,葛汝剛,黃小原.商業信用–廣告合作的供應鏈兩部定價契約協調.工業工程與管理,2010,15(2):41–45. Yu L P,Ge R G,Huang X Y.Supply chain two part pricing contract coordination based on trade credit and advertisement cooperation.Industrial Engineering and Management,2010,15(2):41–45.(in Chinese)

[8]Romano R E.Double moral hazard and resale price maintenance.The RAND Journal of Economics,1994,25(3):455–466.

[9]Roels G,Karmarkar U,Carr S.Contracting for collaborative services.Management Science,2010,56(5):849–863.

[10]吳剛,李傳昭,吳丙山.供應商–銷售商聯合促銷報酬契約設計.管理工程學報,2010,24(3):132–135. Wu G,Li C Z,Wu B S.Compensate contract design of supplier-retailer’s coordinative sale promotion.Journal of Industrial Engineering and Engineering Management,2010,24(3):132–135.(in Chinese)

[11]張旭梅,沈娜利,鄧流生.供應鏈環境下考慮雙邊道德風險的客戶知識協同獲取契約設計.預測,2011,30(4):20–24. Zhang X M,Shen N L,Deng L S.Contract on customer knowledge collaborative capture based on double-sided moral hazard in supply chain.Forecasting,2011,30(4):20–24.(in Chinese)

[12]Cobett C J,Decroix G A,Ha A Y.Optimal shared-savings contracts in supply chains:Linear contracts and double moral hazard.European Journal of Operational Research.2005,163(3):653–667.

[13]張欽紅,駱建文.雙邊不完全信息下的供應鏈信用期激勵機制.系統工程理論與實踐,2009,29(9):32–40. Zhang Q H,Luo J W.Coordination of supply chain with trade credit under bilateral information asymmetry.Systems Engineering:Theory&Practice,2009,29(9):32–40.(in Chinese)

[14]孟衛東,代建生,熊維勤,等.基于納什談判的供應商–銷售商聯合促銷線性合約設計.系統工程理論與實踐,2013,33(4):870–877. MengWD,DaiJS,XiongWQ,etal.Linearcontractdesignforsupplier-retailerjointpromotionbasedonNashbargaining.Systems Engineering:Theory&Practice,2013,33(4):870–877.(in Chinese)

[15]Brown A O,Tang C S.The impact of alternative performance measures on single-period inventory policy.Journal of Industrial and Management Organization,2006,2(3):297–318.

[16]Schweitzer M E,Cachon G P.Decision bias in the newsvendor problem with a known demand distribution:Experimental evidence.Management Science,2000,46(3):404–420.

[17]Choi T M.Li D,Yan H.Mean-variance analysis of a single supplier and retailer supply chain under a returns policy.European Journal of Operational Research,2008,184(1):356–376.

[18]代建生,孟衛東.風險規避下具有促銷效應的收益共享契約.管理科學學報,2014,17(5):25-34. Dai J S,Meng W D.Revenue sharing contract for a risk-averse supply chain with promotional effect.Journal of Management Sciences in China,2014,17(5):25-34.(in Chinese)

[19]Gan X,Sethi S P,Yan H.Coordination of supply chains with risk-averse agents//Choi T M,Cheng T C E.ed.,Supply Chain Coordination under Uncertainty.Berlin:Springer-Verlag,2011:3–31.

[20]Bouakiz M,Sobel M.Inventory control with an exponential utility criterion.Operations Research,1992,40(3):603–608.

[21]Chen X,Sim M,Simchi-Levi D,et al.Risk aversion in inventory management.Operations Research,2007,55(5):828–842.

[22]Choi S,Ruszczyński A.A multi-product risk-averse newsvendor with exponential utility function.European Journal of Operational Research,2011,214(1):78–84.

[23]He Y,Zhao X.Coordination in multi-echelon supply chain under supply and demand uncertainty.International Journal of Production Economics,2012,139(1):106–115.

[24]林宏偉,邵培基,余步雷.基于風險規避的網絡廣告兩階段收益定價模型.系統工程學報,2013,28(3):32–337. Lin H W,Shao P J,Yu B L.Two-stage revenue pricing model for internet advertising with the risk-aversion.Journal of Systems Engineering,2013,28(3):32–337.(in Chinese)

[25]代建生,孟衛東.團隊生產中的利益分享機制設計研究.中國管理科學.2010,18(1):120–127. Dai J S,Meng W D.A study on profit-sharing mechanism in team production.Chinese Journal of Management Science,2010,18(1):120–127.(in Chinese)

[26]Conlon J R.Two new conditions supporting the first-order approach to multi-signal principal-agent problems.Econometrica,2009,77(1):249–278.

[27]Topkis D M.Minimizing a sub-modular function on a lattice.Operations Research,1978,26(2):305–321.

[28]Amir R.Supermodularity and complementarity in economics:An elementary survey.Southern Economic Journal,2005,71(3):636–660.

附錄 文中定理的證明

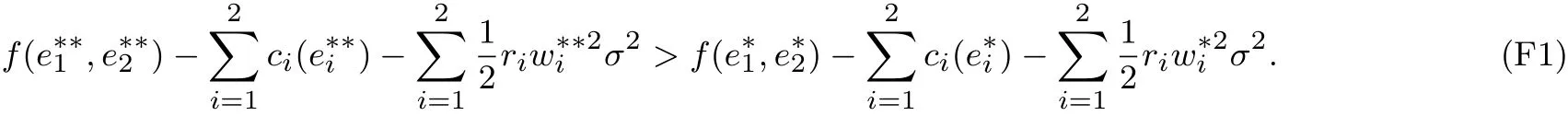
因此,在下面兩式中,必有一個式子成立

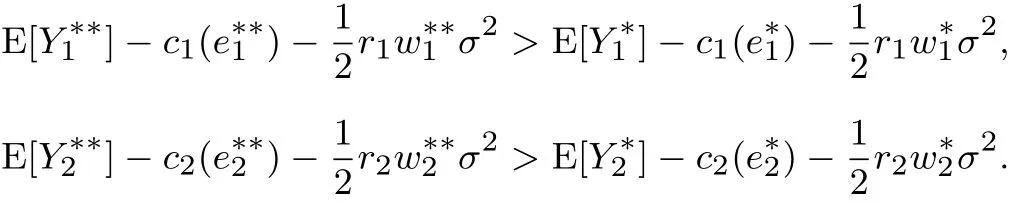
不失一般性,假設前式成立.注意到P2與P3的解域是一樣的,因此,也是P2的可行解.另構造P2的一個可行解,其中t1+t2=0,使得

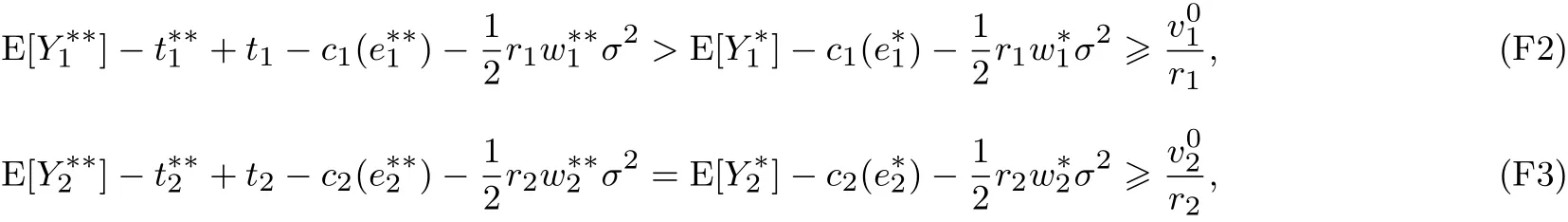
用V來表示P2的目標函數值.式(F2)及式(F3)表明

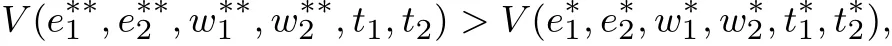
(ii)設P2的解為(e*1,e*2,w*1,w*2,t*1,t*2),由命題1,它也是P3的解.用W來表示P3的目標函數,則有

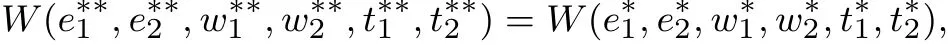
即

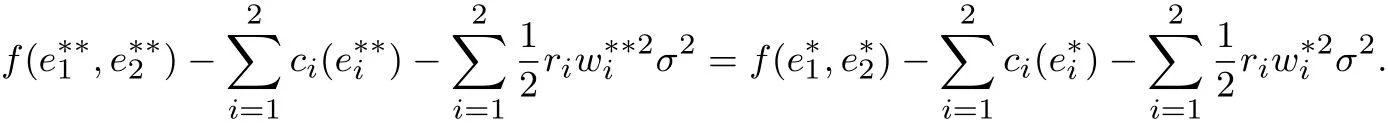
故存在Δt,使得下面兩式同時成立

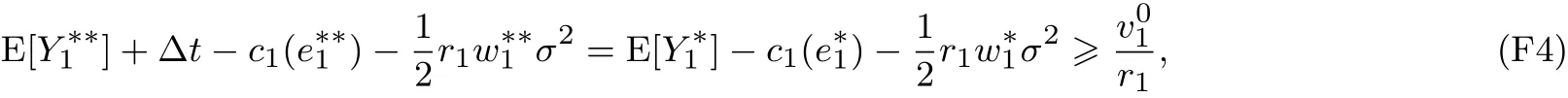
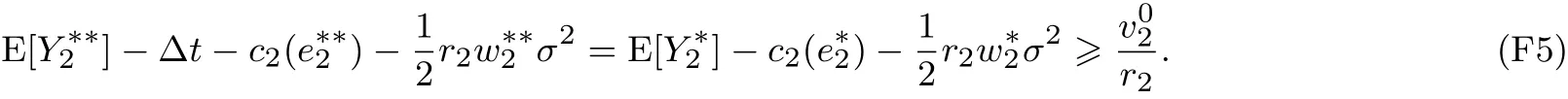
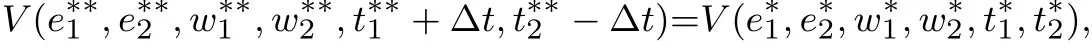
因而它也是P2的解.證畢.

命題3的證明第一部分的證明.首先注意到ri＞0,而根據約束極值理論,又有λi≥0.不失一般性,設τ1=0,則有τ2=1,因λ2≥0,由式(21),必有λ1＞0.

命題4的證明必要性.要使P4有解,要求存在ti,使得,i=1,2,因為關于ti是嚴格增的,因而,i=1,2,BB約束要求

下證式(22)的解存在,令

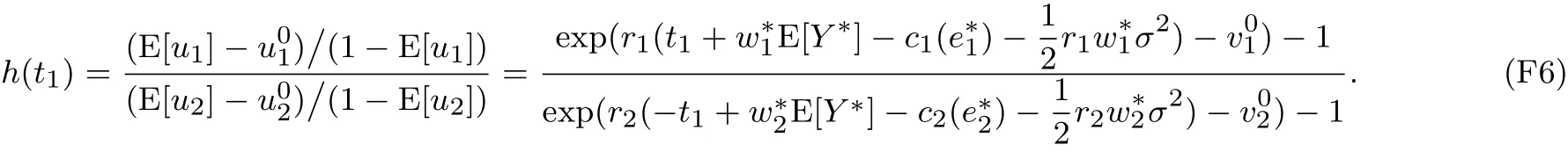
Optimal two-part pricing contract of a risk-averse supply chain

Dai Jiansheng
(Faculty of Management and Economics,Kunming University of Science and Technology,Kunming 650093,China)

This paper studies the optimal two-part linear contract for a supply chain consisting of a manufacturer and a distributor who are risk averse with CARA risk preferences and have bargaining powers,in the presence of bilateral moral hazard.An approach is developed to solve the optimal two-part pricing contract parameters.It investigates the effect of the exogenous variables,such as risk aversion degrees,bargaining powers and reservation utilities of the channel’s member firms,and market demand variability,on the parameters of the optimal contract.It concludes that the optimal wholesale price decreases in the risk aversion degrees of the manufacturer and increases in that of the distributor.Furthermore,a threshold condition is characterized that can determine how market demand variability affects the optimal wholesale price.At last,validity of the conclusions is verified with a numerical example.

supply chain management;two-part pricing;risk aversion;Nash bargaining;bilateral moral hazard

C94;F274

A

1000-5781(2016)01-0066-12

10.13383/j.cnki.jse.2016.01.007

2013-05-21;

2013-12-05.

國家自然科學基金資助項目(71462023;71362025);昆明理工大學人才培養基金資助項目(KKSY201408067);昆明理工大學管理與經濟學院熱點(前沿)領域科研支持計劃項目(QY2015046).

代建生(1978—),男,四川華鎣人,博士,研究方向:供應鏈協調等,Email:jiansheng.dai@163.com.