一種低溫余熱高效利用的氨水動力循環

陳昕，王如竹

?

一種低溫余熱高效利用的氨水動力循環

陳昕，王如竹

（上海交通大學低溫與制冷研究所，上海 200240）

提出了一種高效利用余熱的以氨水溶液為工質的三級壓力動力循環，該循環包含了兩個膨脹做功過程。由于氨水動力循環存在多個自由度且耦合在一起，當余熱溫度和冷凝溫度確定時，循環約束條件能確定高、中、低壓力和氨質量分數自由度的取值范圍。當冷凝溫度確定時，對于不同的余熱溫度和膨脹機進口壓力，最佳循環的選擇可以用圖表顯示且做出參考。在典型工況下當余熱溫度190℃、冷凝溫度30℃時，以熱效率為目標函數的優化計算結果表明熱效率為21.6%，相應的熱力學第二效率為62%。當膨脹機進氣壓在3500 kPa時，余熱溫度在130～190℃范圍內，與KCS11相比改進循環的熱效率提高了8%。在低溫余熱下(>150℃)，改進循環的熱效率要明顯高于Rankine循環和ORC循環。

二元混合物；熱力學；優化；氨水溶液；動力循環；Kalina循環

引 言

低溫余熱驅動以氨水溶液為工質的熱力學循環可以應用在制冷、熱泵、動力或冷電熱聯供等領域，因而受到了研究者廣泛的關注[1-5]。當余熱溫度較低時，使用傳統的以水為工質的朗肯循環不能有效地將余熱轉化為輸出功，Kalina首先提出了以氨水溶液為工質的一系列動力循環[6]，被命名為Kalina循環，在中低溫熱源下，Kalina循環的熱效率能比以水為工質的傳統Rankine循環提高32%[7]。與單一物質水不同，氨水混合物在相變過程中溫度會發生改變，這一性質是提高熱效率的主要原因，通過與有限熱容量的熱源和冷源溫度匹配，可以分別提高吸熱過程和降低放熱過程中的平均溫度，同時，在換熱器中，恰當的冷熱物流溫度匹配能減少傳熱過程中不可逆損失[8]。

由于Kalina循環能有效利用低-中溫余熱，根據熱源品位不同，人們已經在基礎循環的基礎上得到了一系列Kalina循環應用方案，如直燃式KCS5應用在熱源溫度高于648℃[9]，KCS34應用在余熱溫度低于121℃低溫熱源[10]，KCS11應用在余熱溫度低于204℃中低溫熱源[11]。Hettiarachchi等[12]對KCS11進行優化計算余熱溫度為90℃時熱效率為11%。除了使用氨水溶液為工質，其他非共沸混合物（R32和R601a）應用在KCS11在特定工況下熱效率比氨水溶液要高[13]。KCS11存在著多自由度的設計參數[14-16]，如膨脹機進氣壓、排氣壓和氨質量分數，它們的取值范圍受到約束條件的制約，但是在文獻中沒有詳細的設計參數的選值流程，如果膨脹機中工質干度較低時，液滴會影響膨脹機的性能，而且會對膨脹機造成腐蝕，從而增大運行成本[17-18]，所以必須滿足膨脹機出氣的干度是一個約束條件。為滿足約束條件，本文提出了確定設計參數的取值范圍的方法。提出的改進動力循環包含兩個膨脹做功過程，所以對于中間壓力的選擇會影響循環的熱效率。與傳統的兩級壓力系統相比，改進循環設置三級壓力是考慮當余熱溫度較低或者進入膨脹機進氣壓力較高時，能提高膨脹機出口蒸汽的干度，排氣壓力可以適當降低從而提高熱效率。改進動力循環的熱力學建模是利用EES（Engineering Equation Solver）熱力學分析軟件。

1 循環介紹

與圖1中KCS11相比，改進循環的不同之處如圖2所示，從余熱鍋爐出來的過熱蒸汽進入膨脹機1，做功后的氨水氣液混合物分流，一股再次進入熱鍋爐加熱成過熱蒸汽進入膨脹機2，做功后進入回熱器被從泵2流出的過冷氨水溶液預冷，再流經冷凝器向環境排熱，經泵1升壓后在絕熱混合器中與另一部分在狀態點2分流的氣液混合，兩股分流混合后（狀態點10）再經泵2升壓流經回熱器預熱。最后進入余熱鍋爐加熱完成循環。在絕熱混合器中，狀態點4為兩相溶液，狀態點9為過冷狀態，分流比定義為4/2,分流比的選擇是滿足狀態點10為飽和溶液或者過冷狀態。

通常而言，余熱溫度和冷凝溫度是已知條件，但是循環中的膨脹機1進氣壓力（高壓），排氣壓力（中壓），膨脹機2排氣壓力（低壓），氨水溶液質量分數和分流比都是設計參數，所以循環存在5個自由度。但是這5個自由度的取值范圍可以由約束條件來確定。表1包含了6個狀態點的干度約束條件，其中約束條件1和2是為了滿足膨脹機1和2進氣至少為飽和氣態；約束條件3和4是為了保證膨脹機出口干度至少為0.95以避免液滴損壞膨脹機葉片；約束條件5是為了在給定冷凝溫度條件下能被冷卻水冷卻；約束條件6是保證絕熱混合器出口為飽和液體或過冷狀態（>1:過熱狀態；<0:過冷狀態）。

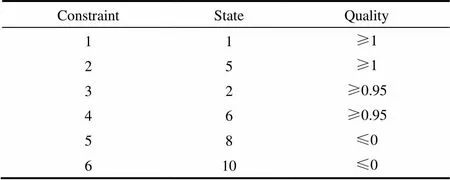
表1 6個狀態點干度約束條件 Table 1 Quality constraint for 6 states

為了方便分析，將圖2中(1,5)、8、1、2和6分別代替為H、L、H、M和L。下角標H、M和L分別表示高、中和低。在建立循環數學模型之前，預先假設的條件見表2。

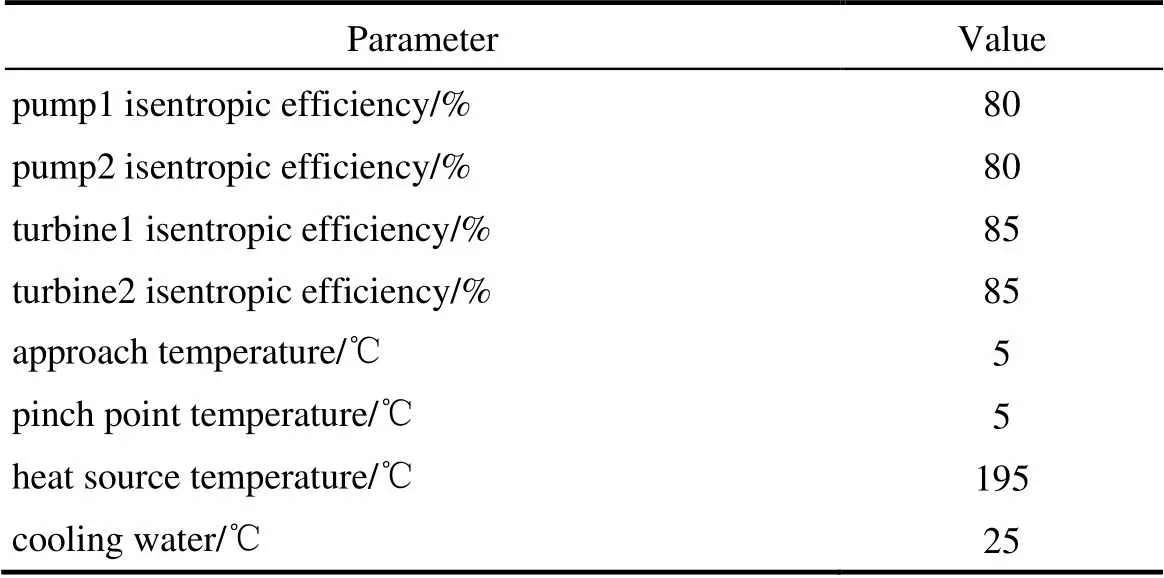
表2 循環建模中假設的輸入參數 Table 2 Assumed input parameters for simulation

1.1 氨質量分數的確定

只要設計參數H、M和L確定，氨質量分數可取范圍可由表1中的約束條件確定：

約束條件1和2

min1=(H,H,2=1) (1)

約束條件5

式中，為干度。式（1）是求得滿足進入膨脹機1和2氨水為飽和氣態最小的氨質量分數，因為在氨水溶液中，壓力和質量分數是正比關系，所以式中壓力為H,計算得到的min1也能滿足當M時干度的要求。式（2）是計算為了將氨水溶液能被冷卻到飽和液態的最大氨質量分數。當選擇的質量分數小于此值時均能保證氨水可被冷卻。

約束條件3和4

式（3）、式（4）中turbine1和turbine2分別為膨脹機1和2的等熵效率，對于求得min2的詳細計算步驟如下

式中，和分別是熵和焓，Ms是當膨脹機等熵效率為1時排氣焓值。因為式（5）是隱函數，所以在計算過程中需要迭代求得min2，同樣地，min3也是按照類似的方法求得。綜上，在給定設計參數時氨質量分數的取值范圍為

1.2H、M和L的設計流程

1.2.1 高壓H對氨質量分數的影響

如圖3所示，隨著H的升高min也隨之升高，可選取的氨質量分數的范圍也隨之縮小。如果膨脹機等熵效率提升，質量分數范圍也會進一步縮小。

1.2.2 中間壓M取值范圍

如圖4所示，在給定H和L后，隨著M的增加，分段函數min沿著min2，min1和min3變化。只有中間壓力M在某一范圍內時，定義該范圍臨界值為M1和M2，max才會大于min，此時才有可供選擇的氨質量分數。計算M1是令式（2）、式（3）相等，而計算M2是令式（2）、式（4）相等。

其中，一個隱含條件為M1≥L,否則就失去了使用膨脹機2的意義，定義存在低壓為Lmax，使得M1與之相等，所以Lmax可以由式（7）求得

另外，觀察圖4，min函數為“U”形，底部值為min1，當L降低時，max也會隨之降低，若降低到小于min1，此時無法選取M，定義該低壓為Lmin。令式（1）、式（2）相等，有

式（10）、式（11）與M無關，所以，在未確定設計參數M時，L的取值范圍由式（10）、式（11）所確定

1.2.3 低壓L設計范圍

在[Lmin，Lmax]范圍內M1和M2隨L的變化關系如圖5所示。M1、M2和Lmin、Lmax的交點分別定義為MA、MB、MC、MD。這4個點的求解令式（7）、式（8）中LLmin和LLmax得出，所以這4個點也與M無關，求得的值見表3。在由M1、M2、Lmin和Lmax組成的閉合空間內分為3個區域，當M的取值在區域1或3內，相對應所能選擇的L各不相同，如當M在區域1內，L選擇的最小值為M1和M的交點，求解為令式（7）中M1M，交點坐標為（L1,M1）。同理，當M在區域3內，L選擇的最小值為M2和M的交點，求解為令式（8）中M2M，交點坐標為（L2,M2）。然而M在區域2內，L選擇的最小值即為Lmin。對于這3個區域內，L相對應的取值范圍為

區域1：

區域2：

區域3：

式中，L1和L2由式（16）、式（17）求得

表3 pMA、pMB、pMC、pMD、pLmin和pLmax的值 Table 3 Value of pMA, pMB, pMC, pMD, pLmin and pLmax

根據以上的分析，在給定H、H和L，可按圖6求出中壓M的取值范圍，根據用戶設計的M，得出L的允許范圍，在根據用戶最終確定的M和L計算出氨質量分數的取值范圍。

2 循環熱力學參數分析

循環熱力學模型是由氨質量分數守恒、質量守恒和能量守恒所建立，前文所述約束條件6是通過分流比來滿足。在H=190℃、L=30℃時，H、M、L和這4個自由度高度耦合，正如前文所述，某個參數變化將會改變其他參數的取值，各個自由度對循環性能的影響可通過參數分析來確定，找出其中關系且試圖將4個自由度解耦。熱效率和熱力學第二效率可分別由式（18）、式（19）求得

式中，t1和t2分別是膨脹機1和2的輸出功；p1和p2分別是泵1和2的消耗功；boiler為余熱鍋爐供熱量；reversible為可逆循環熱效率。

2.1 氨質量分數對熱效率的影響

選取H=3500 kPa和M=2000 kPa，參考圖5，L的選取位于區域2，即L∈[Lmin,Lmax]。表4所示為在此范圍內選擇的L相對應的氨質量分數。對于不同的L,氨質量分數對熱效率的影響如圖7所示，熱效率首先隨著氨質量分數的增加而上升然后下降，所以存在一個氨質量分數opt使得熱效率最高。

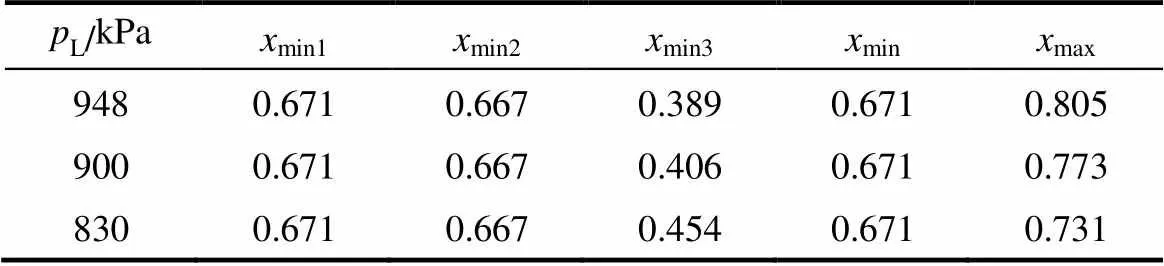
表4 對選擇pL值對應的氨質量分數范圍 Table 4 Range of ammonia mass fraction with respect to corresponding pL

2.2 低壓L對熱效率的影響

選取H=3500 kPa和opt，對于不同的M，低壓L與熱效率的關系如圖8所示，相應的L的取值范圍如表5所示。

表5 對選擇pM值對應的pL范圍 Table 5 Range of pL with respect to corresponding pM

當M的取值在區域1時熱效率最高，在區域1、2和3內，熱效率隨著L的升高先上升后降低，對于固定的中壓存在一個最佳低壓，定義為Lopt。另外，在接下來的分析中，M的取值范圍在區域1內以確保最高熱效率，即M∈[MD,MA]。

2.3 中壓M對熱效率的影響

選取LLopt和opt，圖9所示的是熱效率隨中壓M的變化關系，對于不同的H相對應的M取值范圍如表6所示。對于H3500 kPa或3000 kPa，當M上升時，熱效率首先上升隨之下降。另外，觀察圖9，當H給定時，存在一個最佳的中壓Mopt使熱效率最高。

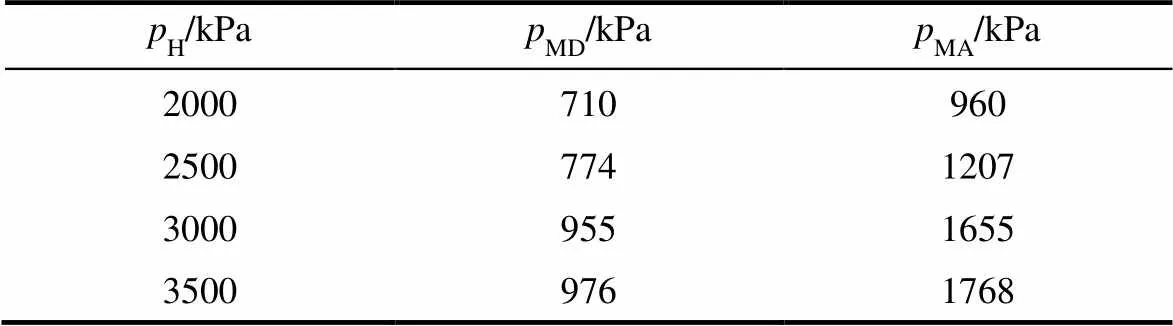
表6 選擇不同pH值時對應的pM范圍 Table 6 Range of pM with respect to corresponding pH

2.4 高壓H對熱效率的影響

選取LL1，opt和MMopt，圖10所示的是對于不同H與熱效率的關系，當H=190℃，熱效率隨著H的上升至最高，定義此點高壓為Hopt，然后趨于平穩。當降低余熱源溫度為180℃，正如預期一樣，熱效率隨高壓變化趨勢相一致，且當熱效率平穩后其值小于190℃時的熱效率。

3 循環熱力學最優化分析

通過前面對4個自由度的參數分析，可以看出在給定H和L，及采用表2的假定，選取LL1，opt，MMopt和HHopt時循環存在著最優熱效率。本文采用的Genetic Optimization 算法，由Charbonneau[19]提出。該算法能很好地找出全局最優值，目標函數定為熱效率。見表7，表1中約束條件全部滿足，5個自由度的取值見表8，另外，只有1.1%的氣液混合物流經絕熱混合器。優化后熱效率為21.6%，熱力學第二效率為62%。

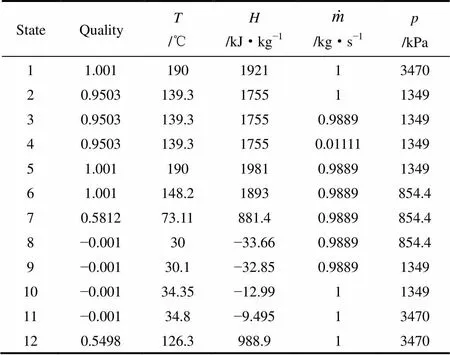
表7 各節點優化結果 Table 7 Tabulated optimization results for each state

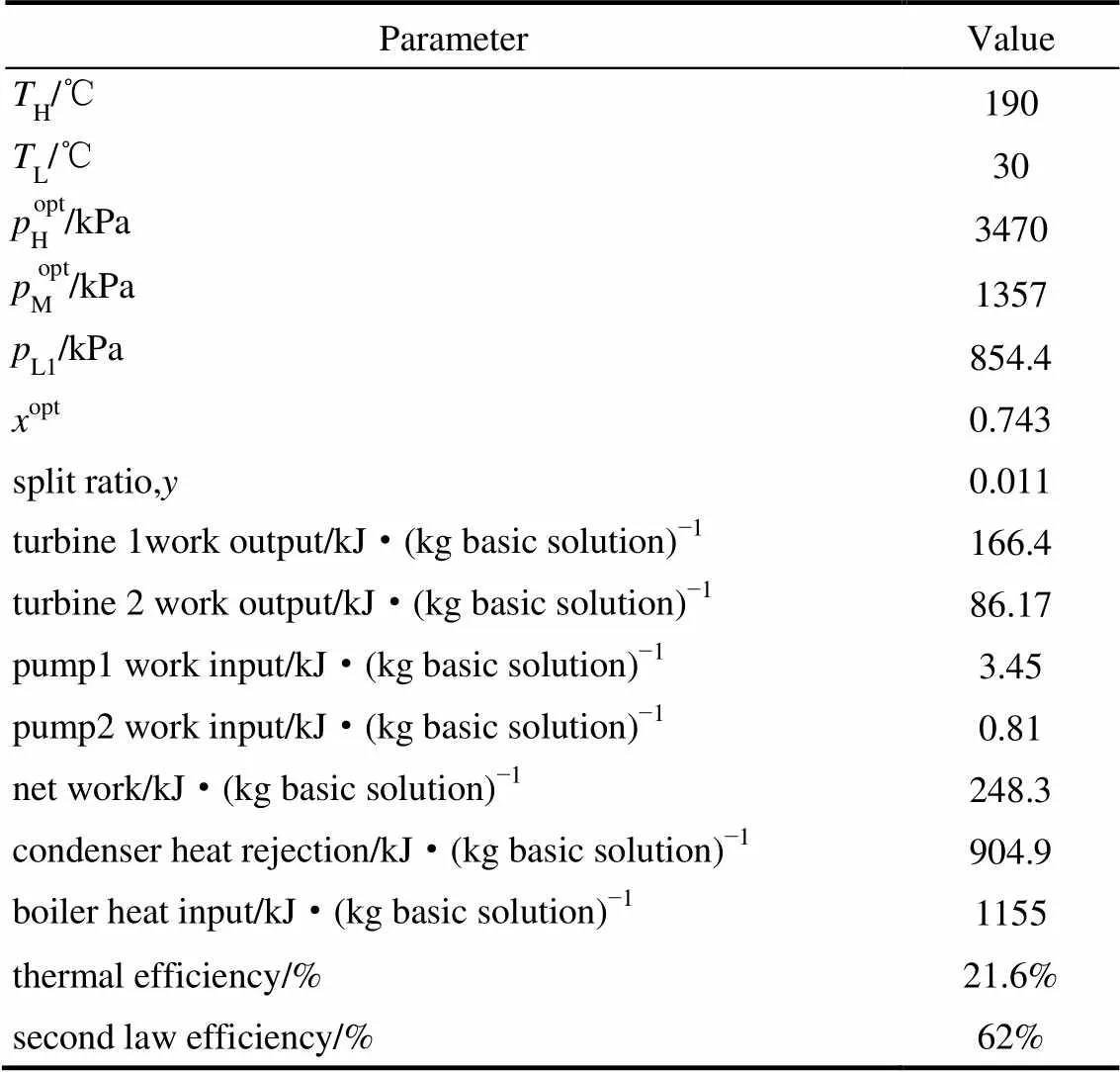
表8 優化計算結果 Table 8 Tabulated optimization results

圖11所示的圖是在優化結果中分數為0.743生成的，圖中3條虛線至上而下分別為恒定HoptMopt和L1壓力下氨水氣液兩相，左右兩邊實線分別表示飽和液態和氣態。因為狀態點2的干度已經達到0.95，如果使用兩級壓力KCS11，膨脹機出氣壓力需大于等于中壓，從而降低了熱效率。

在最優工況下，僅改變分流比，熱效率的變化見圖12，熱效率隨著分流比的增加首先緩慢上升，然后再急劇下降。在最佳分流比附近，熱效率變化很小，如當分流比取為0時，也就是氨水工質經過高壓膨脹機后不需要分流，直接進入余熱鍋爐再過熱，此時熱效率僅降低到21.3%。見表7，再考慮狀態點3為兩相流（干度=0.95），在實際運行中分流兩相流很難確保完全一致的氣液分配比，再由于氣液兩相氨質量分數（0.773/0.207）相差較大，可能會造成進入低壓膨脹機的工質組分發生改變，所以改進循環可以忽略絕熱混合器，這樣能使循環更具有適用性。

4 討 論

對于KCS11可通過類似的自由度設計流程和優化分析求出最優解，當膨脹機進氣壓力恒定為3500 kPa時，改進循環和KCS11隨余熱溫度的變化如圖13所示，改進循環的熱效率明顯高于KCS11。在余熱溫度130～190℃區間內，改進循環的熱效率提高了大致8%。

當余熱溫度為190℃時，改進循環和KCS11隨膨脹機進氣壓的變化如圖14所示，當進氣壓較高時，改進循環的熱效率同樣也高于KCS11。當進氣壓為3778 kPa時，改進循環熱效率提高了9.5%，這是因為改進循環中膨脹機2的排氣壓力能夠低至786 kPa，而KCS11排氣壓力必須為930 kPa滿足排氣干度的約束條件。

在固定冷凝溫度L=30℃時，根據不同的余熱溫度和膨脹機進氣壓，選擇所適宜的循環如圖15所示，當余熱溫度和進氣壓位于在曲線之下應當考慮選擇改進循環，即余熱溫度較低或者進氣壓較高時，改進循環的熱效率要高于KCS11。

圖16所示的是在不同熱源溫度下，改進循環、KCS11、Rankine循環和ORC循環（R245fa）的熱效率對比，其中Rankine和ORC循環中膨脹機和泵的等熵效率如表2所示。Rankine循環熱效率在熱源溫度區間內最低，ORC循環在熱源溫度小于156℃時，其熱效率高于KCS11但小于改進循環。所以改進循環在低溫熱源下能夠具有明顯的優勢。另外在低溫區域內，ORC循環熱效率相比較而言最高[20]，這與計算結果相一致。

5 結 論

本文提出的以氨水為工質的三級壓力動力循環存在著5個自由度，這5個自由度高度耦合，首先當確定了余熱溫度H、高壓H和冷卻水溫度L后，中壓M、低壓L和氨質量分數這3個設計參數的取值范圍通過約束條件來確定。其次，對于循環性能來說，經過參數分析，這3個值又都存在一個最佳值使熱效率最佳，最后經過優化計算，以熱效率為目標函數，計算出最佳的設計參數。當H=190℃和L=30℃時，熱效率為21.6%。與KCS11相比，改進的循環能在余熱溫度H較低或高壓H較高時，熱效率能明顯高于KCS11循環，特別是對于低溫廢熱的合理高效利用提出了有意義的借鑒。

符 號 說 明

H——焓，kJ·kg-1 ? ——質量流，kg·s-1 p——壓力，kPa q——干度 S——熵，kJ·kg-1·K-1 T——溫度，℃ x——氨水質量分數 y——分流比 η——熱效率 上角標 opt——最佳值 下角標 H——高 L——低 M——中 p——泵 t——膨脹機 min——最小值 max——最大值

References

[1] SRIKHIRIN P, APHORNRATANA S, CHUNGPAIBULPATANA S. A review of absorption refrigeration technologies [J]. RenewableSustainable Energy Reviews, 2001, 5(4): 343-372.

[2] DENG J, WANG R Z, HAN G Y. A review of thermally activated cooling technologies for combined cooling, heating and power systems [J]. Progress in EnergyCombustion Science, 2011, 37(2): 172-203.

[3] GOSWAMI D Y. Solar thermal power technology: present status and ideas for the future [J]. Energy Sources, 1998, 20(2): 137-145.

[4] HEROLD K E, RADERMACHER R, KLEIN S A. Absorption Chillers and Heat Pumps [M]. New York: CRC Press, 1996: 189-191.

[5] GOSWAMI D Y, STEFANAKOS E, RAHMAN M M. Analysis of power and cooling cogeneration using ammonia-water mixture [J]. Energy, 2010, 35(12): 4649-4657.

[6] KALINA A I. Generation of energy by means of a working fluid, and regeneration of a working fluid: US 4346561 [P]. 1982-08-31.

[7] ZHANG X, HE M, ZHANG Y. A review of research on the Kalina cycle [J]. RenewableSustainable Energy Reviews, 2012, 16(7): 5309-5318.

[8] LOLOS P A, ROGDAKIS E D. A Kalina power cycle driven by renewable energy sources [J]. Energy, 2009, 34(4): 457-464.

[9] KALINA A I, LEIBOWITZ H M. System design and experimental development of the Kalina cycle technology [J]. Texas AM University, 1987.

[10] NASRUDDIN, USVIKA R, RIFALDI M,Energy and exergy analysis of Kalina cycle system (KCS) 34 with mass fraction ammonia-water mixture variation [J]. Journal of Mechanical ScienceTechnology, 2009, 23(7): 1871-1876.

[11] MLCAK H A. Kalina cycle concepts for low temperature geothermal [J/OL]. Transactions - Geothermal Resources Council, 2002, 26: 707-713. http://pubs.geothermal-library.org/lib/grc/1019685.pdf.

[12] HETTIARACHCHI H D M, GOLUBOVIC M, WOREK W M,. The performance of the Kalina cycle system 11(KCS11) with low-temperature heat sources [J]. Journal of Energy Resources Technology, 2007, 129(3): 243-247.

[13] ELSAYED A, EMBAYE M, ALDADAH R,. Thermodynamic performance of Kalina cycle system 11 (KCS11): feasibility of using alternative zeotropic mixtures [J]. International Journal of Low-Carbon Technologies, 2013, 8(s1): i69-i78.

[14] SUN F, ZHOU W, IKEGAMI Y,. Energy-exergy analysis and optimization of the solar-boosted Kalina cycle system 11 (KCS-11) [J]. Renewable Energy, 2014, 66(6): 268-279.

[15] HE J, LIU C, XU X,. Performance research on modified KCS (Kalina cycle system) 11 without throttle valve [J]. Energy, 2014, 64(1): 389-397.

[16] KIM K H, HAN C H, KIM K. Effects of ammonia concentration on the thermodynamic performances of ammonia-water based power cycles [J]. Thermochimica Acta, 2012, 530(1): 7-16.

[17] MORAN M J, SHAPIRO H N, BOETTNER D D,. Fundamentals of Engineering Thermodynamics [M]. 6th ed. New York: John WileySons Inc., 2007: 340.

[18] GANJEHKAVIRI A, JAAFAR M N M, HOSSEINI S E. Optimization and the effect of steam turbine outlet quality on the output power of a combined cycle power plant [J]. Energy ConversionManagement, 2015, 89(89): 231-243.

[19] CHARBONNEAU P. Genetic algorithms in astronomy and astrophysics [J]. Astrophysical Journal Supplement, 1995, 101(2): 309.

[20] LIN D, ZHU Q, LI X. Thermodynamic comparative analyses between (organic) Rankine cycle and Kalina cycle [J]. Energy Procedia, 2015, 75: 1618-1623.

An efficient ammonia-water power cycle in low temperature waste heat application

CHEN Xin, WANG Ruzhu

(Institute of Refrigeration and Cryogenics, Shanghai Jiao Tong University, Shanghai 200240, China)

An improved ammonia-power cycle activated by low temperature waste heat is operated under three pressure stages，which consists of two turbines. Since there exists many degrees of freedom for ammonia-water power cycle and they are coupled, once the waste heat and condensation temperature are fixed, the selection range of degrees of freedom like three pressure levels and ammonia mass fraction are confined by the cycle constraints. A graphic aid is proposed to select the optimum cycle with various pairs of waste heat temperature and turbine inlet pressure under fixed condensation temperature. For the typical working condition like waste heat and condensation temperature of 190℃ and 30℃, the optimization results shows that the thermal efficiency of 21.6% is obtained and the corresponding second law efficiency is 62%. The thermal efficiency is increased by around 8% when the temperature of waste heat is from 130℃ to 190℃ under a fixed turbine inlet pressure(3500 kPa). The improved cycle increases the performance compared with Rankine cycle and ORC cycle in low temperature waste heat application (>150℃).

binary mixture; thermodynamics; optimization; ammonia water solution; power cycle; Kalina cycle

supported by the Science Fund for Creative Research Groups of the National Natural Science Foundation of China (51521004).

date: 2016-03-09.

Prof. WANG Ruzhu, rzwang@sjtu.edu.cn

TK 11+5

A

0438—1157（2016）09—3536—09

10.11949/j.issn.0438-1157.20160275

國家自然科學基金創新研究群體科學基金項目（51521004）。

2016-03-09收到初稿，2016-05-28收到修改稿。

聯系人：王如竹。第一作者：陳昕（1987—），男，博士研究生。