一類非線性振動方程的定性分析

李　鵬，竇霽虹，仲文林，盧克英

(西北大學 數學學院, 陜西 西安　710127)

?

·數理科學·

一類非線性振動方程的定性分析

李鵬，竇霽虹，仲文林，盧克英

(西北大學 數學學院, 陜西 西安710127)

對一類非線性振動方程進行定性分析與探究,并推廣了此類方程。采用行列式-跡法則、小參數擾動、首次積分和Bendixson-Dulac判別法。證明了方程對任何參數都不存在閉軌線和奇異閉軌線,分析了方程在特殊情形下奇點個數、類型。豐富了已知結果, 使其適用范圍更廣。

振動方程; 定性分析; 閉軌線; 極限環;Dulac判別法

文獻[1]給出了一類由微分方程

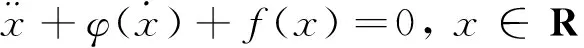
(1)

(2)

在mb≠0時,對任何參數都不存在閉軌線和奇異閉軌線。文獻[2]中未分析式(2)平衡點的類型及其穩定性;也未考慮b=0時,系統極限環的存在性。本文首先在方程(2)的基礎上推廣并得到一類特殊振動方程滿足適當條件后,仍然具有文獻[2]的結論；其次，針對文獻[2]中的不足進行補充。這一探究更加豐富振動方程理論，對于物理學中機械振蕩和周期振蕩的研究具有深刻意義。

引理1[3]設G為單連通域,若存在一次可微函數B1(x,y)與F(x,y),使

在G中保持常號,且不在任何子區域中恒等于零,則方程不存在全部位于G中的閉軌線和奇異閉軌線。

引理2[2](Bendixson-Dulac判別法)若在單連通域G內存在函數B(x,y)∈C1(G),使

且不在G的任何子區域內恒為零,則系統不存在全部位于G內的閉軌線和具有有限個奇點的奇異閉軌線。函數B(x,y)稱為Dulac函數。

引理3[2]設有系統

其中X和Y在O(0,0)鄰域內解析,O(0,0)為其對應線性系統的中心點,若在O(0,0)鄰域S(0,δ)內存在此系統的一個連續的首次積分,則O(0,0)必為中心。

本文主要研究一類非線性振動方程

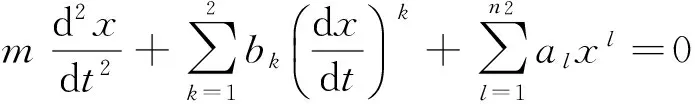
(3)

1　主要定理

定理1若mb1≠0,則方程(3)對于任何參數都不存在閉軌線和具有有限個奇點的奇異閉軌線。

證 明假設振動方程式(3)的更一般形式

(4)

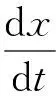
(5)

取E(x,y)≡C1, 其中C1為常數,則

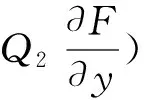
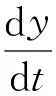
(6)

只有選取F(x,y)≡C2x,其中C2為常數。

對于x,y∈R,要使得式(6)符號確定,則有如下結論:當k=1或2,l=1,2,3，…時,式(6)可以化為

(7)

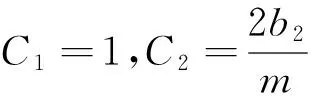
將非線性殊振動方程式(3)進一步推廣為

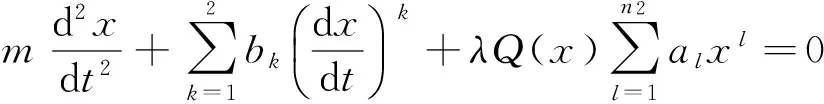
(8)

其中Q(x)是一類關于變量x的非多項式[4-7],并滿足:

1)Q(x)是連續函數,在x=0處具有n階導數;

2)Q(x)在x=0處取值為0,即Q(0)=0;

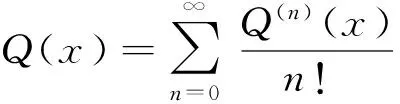
使之也具有對于任何參數都不存在閉軌線和奇異閉軌線,得到如下定理。

定理2若λ≠0，mb1≠0,則振動方程式(8)對于任何參數都不存在閉軌線和具有有限個奇點的奇異閉軌線。

證 明仿照定理1的證明,取E(x,y)≡C3,取F(x,y)≡C4x,其中C3,C4為常數,同樣可得如下結果:

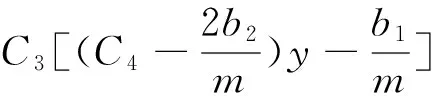
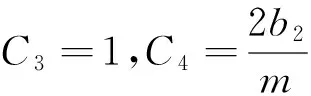
關于定理2,給出2個典型振動方程作為實例通過Matlab軟件對振動方程進行數值模擬[9]。

例1振動方程

(9)

當mb1≠0時，對于任何參數都不存在閉軌線和具有有限個奇點的奇異閉軌線。取m=1.0,b1=-0.3,b2=-0.8,λ=0.4,a1=0.1,a2=0.3,a3=0.4,其余參數為0,軌線圖如圖1所示。

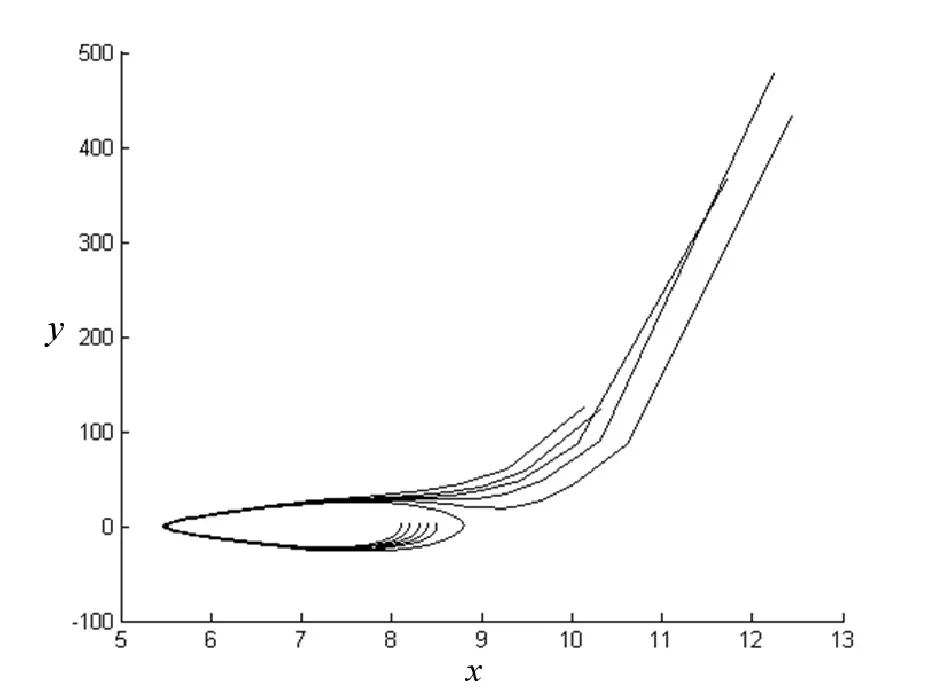
圖1　振動方程式(9)的軌線圖Fig.1　Trajectory of vibration equation (9)

取m=1.0,b1=0.3,b2=-0.8,λ=0.4,a1=0.1,a2=0.3,a3=0.4,其余參數為0,軌線圖如圖2所示。

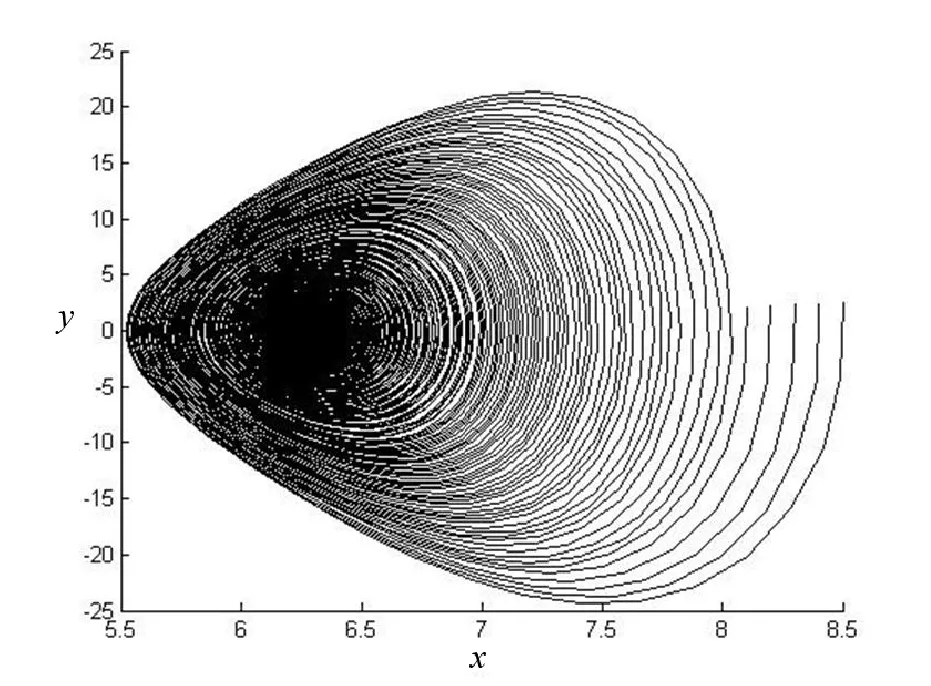
圖2　振動方程式(9)的軌線圖Fig.2　Trajectory of vibration equation (9)

結果分析：只改變b1符號，其他參數值不變時，方程式(9)軌線圖發生改變，但是不存在極限環或奇異閉軌線。

例2振動方程

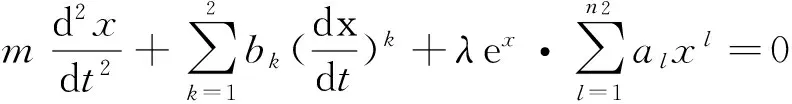
(10)

當mb1≠0時，對于任何參數都不存在閉軌線和具有有限個奇點的奇異閉軌線。取m=1.0,b1=-0.3,b2=-0.8,λ=0.3,a1=0.1,a2=0.3,a3=0.4,其余參數為0,軌線圖如圖3所示。

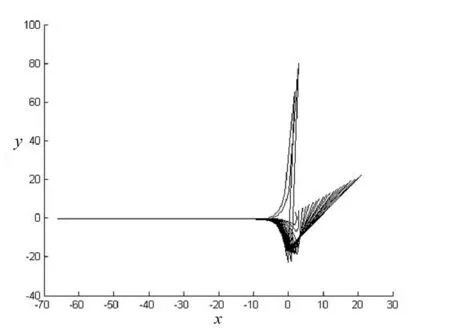
圖3　振動方程式(10)的軌線圖Fig.3　Trajectory of vibration equation (10)

取m=1.0,b1=0.3,b2=-0.8,λ=0.3,a1=0.1,a2=0.3,a3=0.4,其余參數為0,軌線圖如圖4所示。

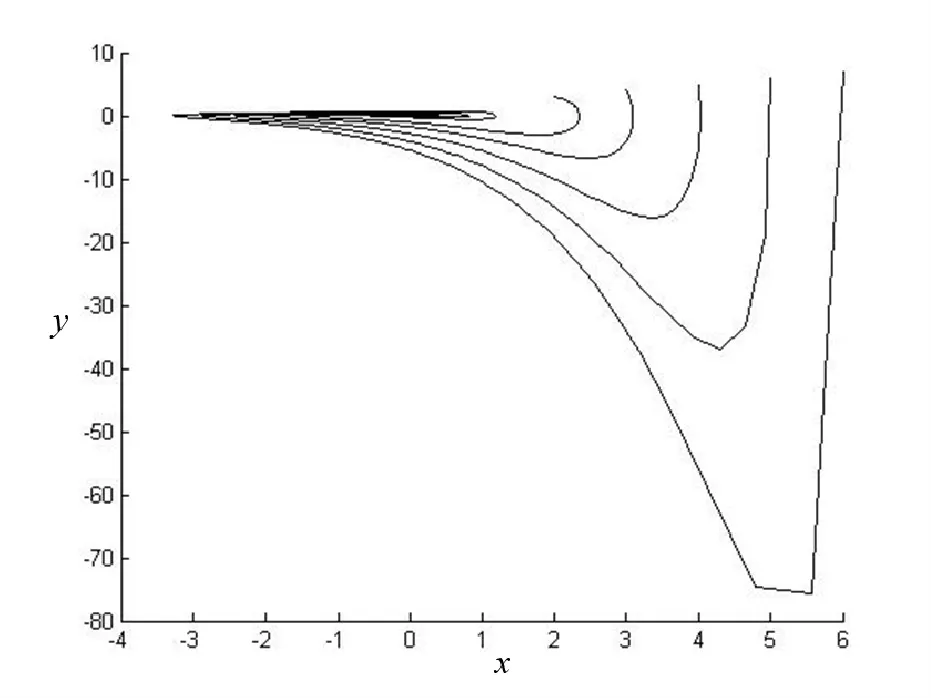
圖4　振動方程(10)式的軌線圖Fig.4　Trajectorg for ribration equation (10)

結果分析:只改變b1符號，其他參數值不變時，方程式(10)軌線圖發生改變，但是不存在極限環或奇異閉軌線。

綜上，由例1和例2中的振動方程式(9)，(10)的軌線圖驗證定理2結論成立。

本文還研究振動方程式(3)特殊情形下的方程:

(11)

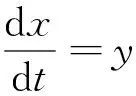
(12)

由定理1可知方程式(11)不存在極限環由于在上述振動方程中m代表質量,故本文只考慮參數m>0時,系統(12)平衡點性態和極限環的存在性。

2　定性分析

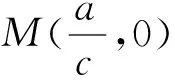
(13)

記p=-tr(D),q=det(D)。

(i)當c=0時,系統只有唯一奇點O(0,0),將其代入式(13)得

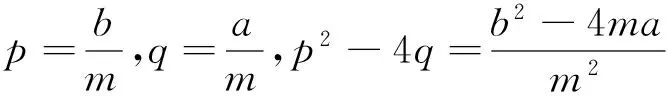
當a<0時,有q<0,故奇點O(0,0)為不穩定鞍點;

當a>0,b>0,b2-4ma>0時,有p>0,q>0,p2-4q>0,故奇點O(0,0)為穩定結點;

當a>0,b<0,b2-4ma>0時,有p<0,q>0,p2-4q>0,故奇點O(0,0)為不穩定結點;

當a>0,b>0,b2-4ma≤0時,有p>0,q>0,p2-4q≤0,故奇點O(0,0)為穩定焦點或穩定臨界結點或穩定退化結點;

當a>0,b<0,b2-4ma≤0時,p<0,q>0,p2-4q≤0,故奇點O(0,0)為不穩定焦點;或不穩定臨界結點或不穩定退化結點;

當a>0,b=0時,有p=0,q>0,故奇點O(0,0)為中心。

當a=0時,系統(12)有奇線y=0。有關奇線的性態在這里不予分析。

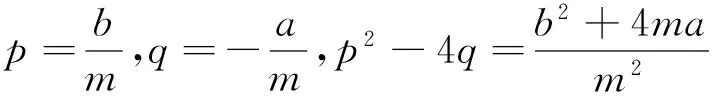
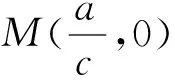
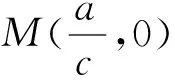
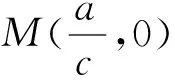
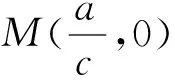
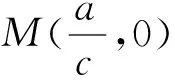
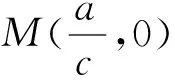
當a=0,c≠0時,有q=0,故奇點O(0,0)是高階奇點,采用小參數擾動法[2]來分析高階奇點的類型。

引入參數ε,0<ε?1,考查輔助系統

(14)

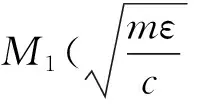
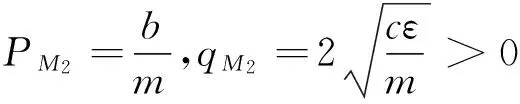
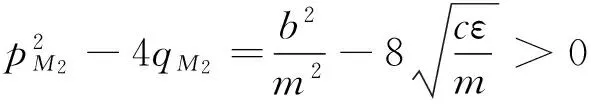
經判斷后可得M1是鞍點;M2為穩定結點。當ε無限靠近時M1和M2均向O點逼近。當ε→0時式(14)就變為

(15)

此時M1和M2在O點重合,從而形成鞍結點。

定理4當b≠0時,對于系統式(12)中任何參數都不存在閉軌線和奇異閉軌線;當b=0時,系統式(12)必存在閉軌線。

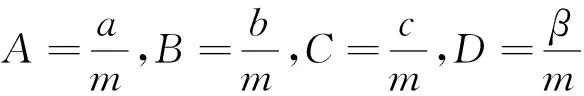
(16)

取Duluc函數B(x,y)=e-2Dx，且當B≠0時，即b≠0時，有

恒成立,故由引理2可知當b≠0時,對于任何參數,系統式(12)都不存在閉軌線和奇異閉軌線。

當B=0,即b=0時,系統(16)是可積的,存在連續的首次積分。

(i)當D=0且B=0時,存在連續的首次積分

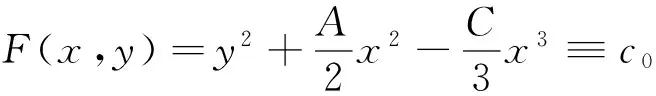
其中c0為任意常數。

(ii)當D≠0，B=0時,也存在連續首次積分。

首先將方程式(16)化為:

(Ax-Cx2-Dy2)dx+ydy=0

(17)

記M(x,y)=Ax-Cx2-Dy2,N(x,y)=y。

由文獻[10]，利用積分因子，將式(9)轉化為恰當微分方程后，可以采用通積分求出式(8)或式(9)的通解。經計算:

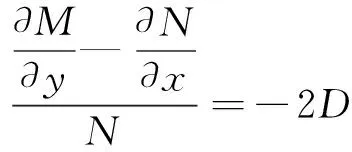
故式(17)的一個積分因

μ(x,y)=e∫-2Ddx=e-2Dx，

則式(17)轉化為一個恰當方程:

μ(x,y)M(x,y)dx+μ(x,y)N(x,y)dy=0。

(18)

對于恰當方程(18)可求得通積分u(x,y)=c,它同時滿足

(19)

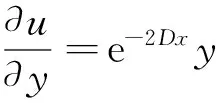
(20)

對式(19)關于x積分得到

(21)

將u(x,y)代入式(20)可得

并代入式(21)，可得

所以方程(17)的通解為

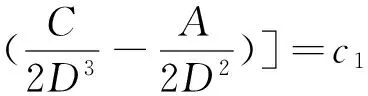
其中c1為任意常數。故方程式(17)的一個連續首次積分為

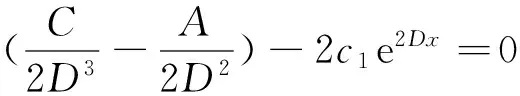
根據定理3可得:當B=0時,即b=0時,O(0,0)為其對應線性系統的中心點。結合引理3可得:當b=0時,O(0,0)必為中心,故系統必存在閉軌線。定理3和4的結論對文獻[2]作了進一步補充。

3　結　論

由于奇點附近軌線分布的復雜性,對其研究是定性分析的重要部分,此外它反映了客觀世界中重要的靜止平衡狀態,有著重要的應用價值[11-13];其次閉軌線,奇異閉軌線和極限環在研究定性結構中扮演著重要角色，反映了現實世界中大量存在的周期振蕩現象。

[1]陸啟韻.常微分方程的定性方法和分叉[M].北京：北京航空航天大學出版社，1989：207-208.

[2]馬知恩,周義倉.常微分方程定性與穩定性方法[M].北京：科學出版社，2015.

[3]葉彥謙.極限環論[M].上海：上海科學技術出版社，1984：14-22.

[4]DUJia,XIAOJian.ExistenceofLimitCyclesforaclassof(n+1)-thPolynomicalsystem[J].ChineseJournalOfEngineeringMathematics，2014,31(2)：274-285.

[5]DUJia,XIAOJian.Limitcycleandbifurcationproblemforaclassofnonpolynomialplanardifferentialsystems[J].CommunicationonAppliedMathematicsandComputation, 2014,128(2)：189-198.

[6]朱勇,姜萬錄.摩擦力作用下電液伺服系統非線性動力學行為[J].北京航空航天大學學報，2015，1：41-01.

[7]李國濤,劉興國.一類非多項式微分系統的定性分析[J].湖南工業大學學報，2008，122(6)：10-12.

[8]韓彥偉,曹慶潔.一類幾何非線性系統的動力學行為及應用研究[D]. 哈爾濱：哈爾濱工業大學，2015：10.

[9]薛定宇,陳陽泉.高等應用數學Matlab求解[M].3版.北京：清華大學出版社，2013：10.

[10] 王高雄,周之銘.常微分方程[M].3版.北京：高等教育出版社，2010：55.

[11] 惠俊鵬,楊超.考慮參數攝動的飛行器氣動伺服彈性魯棒穩定性分析研[J].導彈與航天運載技術，2015,8：1-5.

[12] 羅海洋.受電磁激勵連續轉子系統非線性振動與穩定性[D].大連：大連理工大學，2014.

[13] 張國策.陳立群磁場中懸臂梁的非線性振動[D].上海：上海大學，2014.

(編輯亢小玉)

The qualitative analysis of a type of Nonlinear vibration equation

LI Peng, DOU Ji-hong, ZHONG Wen-lin, LU Ke-ying

(School of Mathematics, Northwest University, Xi′an 710127， China)

To do qualitative analysis of and exploration for a special type of vibration equation, at last the promotion and extension of the equation were done.The determinant of trace rule, small parameter perturbation, the first integral and Bendixson-Dulac discriminant are applied into the analysis on the vibration equation for qualitative analysis. Under different parameters, the number and type of singularities was proved.In the sequel, to prove that the equation for any parameters doesn′t exist closed trajectories and the singular closed trajectories. The obtained results improve and expand the related known works.

vibration equation; qualitative analysis; closed trajectories; limit cycle; Dulac discriminant method

2015-04-03

西北大學研究生自主創新基金資助項目(YZZ14083)；陜西省教育廳自然科學專項基金資助項目(CU063120603000)

李鵬，男，山西忻州人，從事微分方程定性與穩定性研究。

竇霽虹，女，陜西西安人，教授，從事微分方程定性理論研究。

O175.12

A

10.16152/j.cnki.xdxbzr.2016-04-001