明末清初太陽視差在中國的傳播

張　祺,宋芝業

(內蒙古師范大學 科學技術史研究院,內蒙古 呼和浩特　010022)

?

明末清初太陽視差在中國的傳播

張祺,宋芝業

(內蒙古師范大學 科學技術史研究院,內蒙古 呼和浩特010022)

明末清初之際，太陽視差傳入中國,并被積極引入官方歷法。從《崇禎歷書》到《歷象考成后編》均對其進行了不同程度的整理與修正,理論層面上已經與西方相差不遠,但由于中國天文學以實用為中心的價值取向,僅將其作為歷法計算的重要參數,未能產生類似于西方的影響。通過對比幾部官方歷法中太陽視差的相關記述,研究清代歷算家對該項知識的3次主要修改,并在此基礎上分析清代歷算家對太陽視差的認識程度以及科學訴求。關鍵詞：視差;天文單位;歷法

太陽視差又稱太陽赤道地平視差,在雷達天文學問世之前,地月系質心到太陽的距離,即天文單位,皆需通過太陽視差測定。近幾個世紀以來,太陽視差一直是天文學的重要問題。1672年火星沖日期間,卡西尼及其助手通過觀測數據推算出了當時最為精確的太陽視差,將原先的日地距離擴大了近20倍,引起西方學術界極大的轟動。1738年《歷象考成后編》編撰時,將卡西尼的觀測數據及推算方法收入其中,但卻并沒有產生類似西方的轟動效應。本文基于原始文獻,通過比對明末清初直至乾嘉時代的幾部官方歷法著作,分析當時學者對太陽視差的理解方式,進而了解中國歷算家對太陽視差的認識程度以及科學訴求。

1　《崇禎歷書》中的太陽視差

最早傳入中國的西方視差知識,見于1605年由利瑪竇(Matteo Ricci,1552—1610)與李之藻(1565—1630)合譯的《乾坤體義》。該書主要介紹地圓說、地球五帶劃分、行星內外順序等西學基礎知識。文中討論“日球大于地球,地球大于月球”時繪有一圖,名為“測量月離地幾何式”,其中就包含一些地平視差知識。

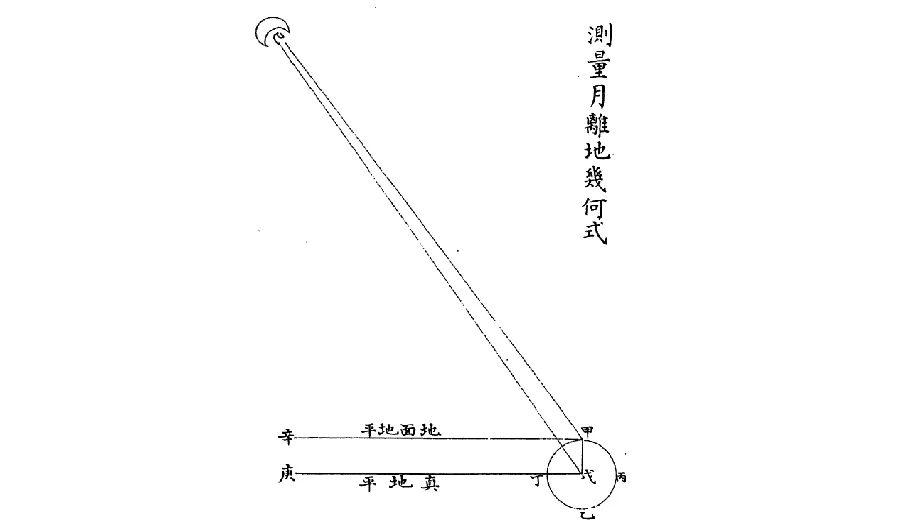
圖1　《乾坤體義》中的月地距離計算模型Fig.1　Calculation model of the distance between Month and Earth

假如甲乙丙丁為地球,戊為其心,甲戊為地球半徑,己為月,戊庚真地平,甲辛地面地平也。從甲地面欲測己戊線,乃月離地心里數之幾何矣[1]。

這是一段介紹月地距離計算方法的文字,后文具體算法中先后用到了“真地平高度”與“視地平高度”,并指明它們之間的差異,該差異其實就是地平視差。文中雖未明確使用這一概念,但已經相當于用地平視差求解月地距離。

1607年,李之藻與利瑪竇合譯的實用天文學著作《渾蓋通憲圖說》出版,其中的“地平規說”再次提及地平視差的相關知識。

此規應設二規,一當地中半處,一當地面。若太陽、金星及木、火、土三星離地絕遠,即以地中做平規,算法亦無差。若算太陰及金、水二星,離地不甚遠,則當就地面起算,方得確度耳[2]。

文中主要介紹地平規的用法,主張將行星的地平視差按距離分為兩類,其中月亮、金星、水星離地心較近,視差較大。而太陽、土、木、火三星及恒星離地較遠,視差微乎其微,可忽略不計。

1612年,王英明《歷體略》刊出,該書主要是一部介紹中西天文學的通俗性著作。書中關于地平視差亦有所涉及,但內容與之前著作大同小異,如其言道:

太陽當空,列曜俱熄,至夜而星可測也。星莫燦于五緯,然各有遲留退伏。又金、水、太陰距地最近,不可以地面為較。自太陽以上,諸曜距地絕遠,則地面、地心總之不異[3]。

明末清初之際的天文歷法著作中,介紹地平視差最為全面、理論最為系統的,當推徐光啟(1562—1633)率同湯若望(Johann Adam Schall von Bell,1591—1666)、羅雅谷(Giacomo Rho,1593—1638)等傳教士編撰的《崇禎歷書》。入清以后,該書又由湯若望等人略加刪改,更名為《西洋新法歷書》。《崇禎歷書》成書于1634年,書中對日、月、五星地平視差的概念、幾何原理、觀測中的作用、《地半徑差表》的構造方法都做出了較為詳細的論述。特別值得注意的是,修改了之前著作中無需考慮太陽視差的說法,對這一問題給予了足夠的重視。如《崇禎歷書·日躔歷指》開篇即批評古法測冬、夏至日高時,未考慮到“人目不在地心在地面,故得數未確。”[4]相對于中國傳統測量方法及早期的西學普及性著作,可說是一個較大的變化。

關于太陽視差的幾何原理及觀測中的作用,《崇禎歷書》主要通過作圖明之:

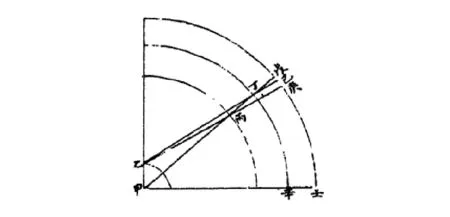
圖2　《崇禎歷書》中的地平視差Fig.2　The horizontal parallax in "Chong Zhen Li Shu"

如上圖,甲為地心,甲乙為地半徑,丁辛為日躔最高圈,日行在最高丁,人見日躔于外天巳,壬巳弧為其地平上之視高。然從地心測之,則壬戊為其地平上之實高,兩高之差為戊丁巳角或乙丁甲角。若日行高沖丙,從地心測其實高仍在戊,與在最高丁等,則從地面乙視之,見日躔于外天庚……故太陽之實高等,隨時所見視高不等,其視差之數亦不等[4]。

《崇禎歷書》通過作圖說明了太陽視差的幾何意義,可視為明末清初以來最為詳細的介紹。除作圖說明外,《崇禎歷書》較大的亮點是給出了《地半徑差表》及其造表法,具體流程主要分為兩步:

步驟一:在偏心圓模型下求得日地的距離

如圖3:丙為地心,戊為太陽位置,乙為太陽本天心,乙丙為兩心差e=358416,甲戊弧為太陽平行度M0、甲乙為太陽本天半徑R1=10000000。通過模型的幾何推導,求得日地距離為:

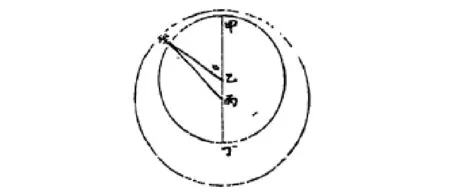
圖3　《崇禎歷書》中的太陽運動模型Fig.3　The model of sun′s motion in "Chong Zhen Li Shu"

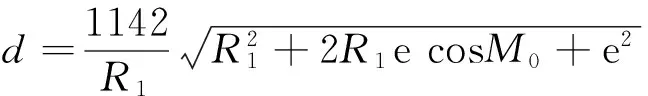
在求解過程中,《崇禎歷書》預先設定地球半徑與太陽本天半徑之比例為1∶1142,該數據引自哥白尼《天體運行論》,但本身誤差較大,這也就成了太陽視差數值偏大的主要原因。

步驟二:求解太陽視差

如圖4:丙為地心,丁為地面,乙為太陽,則甲乙為太陽天頂距z1,乙角即為地半徑差p,則有:

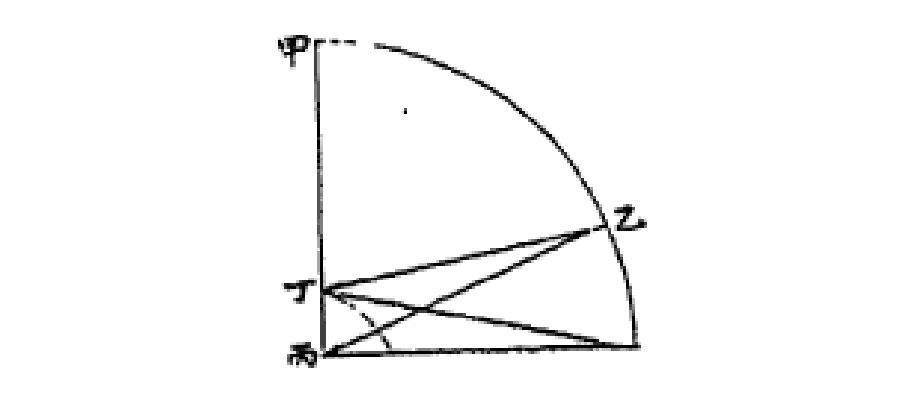
圖4　《崇禎歷書》中的視差模型Fig.4　The model of parallax in "Chong Zhen Li Shu"

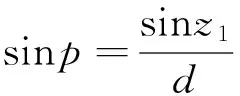
其中p即為太陽在該位置處的視差。

《崇禎歷書》解釋了太陽視差的計算原理,但模型中一些常數的求解方法卻并未交待,理論上仍有混亂之處。具體造表時,只依據模型數據選取近地點、遠地點、中間點三段距離列表。若太陽處于其他位置,則依據“夏至左右三宮屬最高,春秋分各左右三宮屬中距,冬至左右三宮屬最高沖”[4]的原則選取表中數據。但如此一來,造表法中求解日地距離d的步驟似乎又顯得多余了。《歷象考成》重編《地半徑差表》時,雖模仿《崇禎歷書》以近、遠、中三位置列表,但各位置的日地距離卻采用國內觀測數據重新計算,邏輯上更合理一些。

2　《歷象考成》中的太陽視差

1635年《崇禎歷書》編成后,就不斷遭到保守派的激烈反對,直至1644年明朝滅亡,始終未能頒行[5]。其修改本《西洋新法歷書》由于時間倉促,書中依然存在著諸如圖表不和、各種天文理論之間較為雜亂等不足之處,后雖經南懷仁等人幾次修訂,但情況并未改觀。1713年康熙帝又親自招梅瑴成、何國宗等大批學者,在榮親王允祿、莊親王允祉的主持下重新編訂歷書,《歷象考成》的編訂工作于康熙六十一年(1722年)結束,共成四十二卷。

《歷象考成》與《崇禎歷書》的理論系出同源,但具體內容卻做了許多修改。知識結構更加的詳細、具體,也更易于讀者理解。關于視差的基本概念,《歷象考成》解釋為:

凡求七曜出地之高度必用測量,乃測量所得之數與推步所得之數往往不合。蓋推步所得者,七曜距地心之高度,而測量所得者,七曜距地面之高度也。距地心之高度為真高,距地面之高度為視高,人在地面不在地心,故視高必小于真高,以有地半徑差也。蓋七曜恒星雖皆麗于天,而其高下又各不等,惟恒星天為最高,其距地最遠,地半徑差甚微,故無視高、真高之差若夫七曜諸天,則皆有地半徑差。今欲求太陽之真高,必先得地半徑差,欲求地半徑差,必先得地半徑與日天半徑之比例。[6]

《歷象考成》從觀測、幾何原理、影響參數等多方面介紹了地半徑差的基本情況,知識層面上雖未出《崇禎歷書》范圍,但內容更顯詳盡,圖像也更為精美、細致。

相對而言,《歷象考成》最大的改變在于《地半徑差表》的重編及其造表法的改進。《崇禎歷書》的視差造表法需先以太陽模型推出不同位置的日地距離,而《歷象考成》由于采用了中國本土學者改進的太陽模型,《崇禎歷書》中的數據及方法明顯不再適用。況且按一般規律,日地距離本應以視差推得,《崇禎歷書》卻反其道而行之,似乎也有邏輯顛倒之嫌。基于上述原因,《歷象考成》補充了一種通過觀測太陽視高度推算日地距離的方法,并以之重新排算《地半徑差表》*《崇禎歷書》中曾用該方法求解月地距離，亦曾言日地距離也可用此方法求得，但并未給出求解日地距離的具體步驟。《歷象考成》編撰時，將之編入求解地半徑差的相關章節中，具體步驟考慮到最高、最卑、中距處的不同特點，解說亦有所發揮。。

如圖5:甲為地心,乙為暢春園地面,庚為暢春園天頂,子為廣州府地面,丑為廣州府天頂,戊為太陽,寅為赤道所在。設地半徑r=10000000,根據北京、廣州的地理緯度,可得兩地天頂距之差,即丑庚弧φ=16°49′30″。

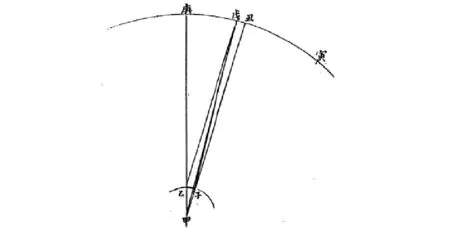
圖5　《歷象考成》中的地平視差Fig.5　The horizontal parallax in "Li Xiang Kao Cheng"

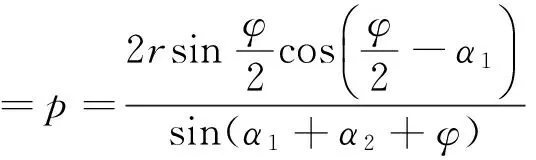
2)測算太陽“中距”處日地距離時,需在春分后八日左右觀測暢春園與廣州府正午地平高度,所用方法與計算太陽“最高”基本相同,但《歷象考成》將時差的影響也考慮在內,較有新意。

測得廣州府子午線在京師之西三度三十三分,其午正時乃京師午正初刻十四分也。夫太陽距緯度夏至時每日只差四十余秒,其一刻所差甚微,可不論。若春分時每日差至二十四分,則十四分時可差一十四秒。又春分后太陽自卑而高,緯度既差一十四秒,則午正之高度亦多一十四秒。故必于所測之度減去緯差,始為與京師子午相當地面之高度也[6]。

由于時差的影響,廣州府太陽地平高度需減去十四秒,方可得到與京師近乎相同緯度的太陽視地平高度。《歷象考成》考慮到時差及太陽地平高度快慢的變化,理論上是較為合理的。依此法,可求得太陽“中距”時日地距離約為1142地半徑,與《崇禎歷書》相同。

3)《歷象考成》測算太陽在本天“最卑”處的日地距離時,沒有繼續采用觀測數據推算,而是采用了模型基本常數間的比例關系:

《歷象考成》舍觀測而取比例,主要是為了回避冬至時較大的蒙氣差。即所謂:“欲以實測求之,奈冬至前后太陽躔本天最卑時,高弧僅二十六度余,蒙氣差甚大,難得其真”。[6]“最高”、“中距”、“最卑”三段日地距離推出后,即可利用《崇禎歷書》方法計算相應地半徑差值。

總體而言,《歷象考成》對《崇禎歷書》中的地半徑差知識進行了較好的查缺補漏。在計算中考慮到諸如時差、蒙氣差等因素的影響,使得算法結構更加嚴密,可見清初歷家對西方這套計算模型的掌握已較為熟練。不足的是《歷象考成》之法僅在理論上可行,太陽視差本身過于微小,具體操作時同樣會遭遇這些細微差距不易觀測的事實,數據相較《崇禎歷書》僅在秒的數量級有所改變,總體精度提高不大。

3　《歷象考成后編》中的太陽視差

《歷象考成》的編撰是中國學者對西方天文歷法進行獨立整理的一次嘗試,也做出一些有益調整與改進,但其基本內容還是屬于西方古典天文學范疇,與歐洲同時代天文理論相比較為落后,誤差之處在行用不久即開始顯現。雍正八年(公元1730年),傳教士戴進賢(Ignatius Kgler,1680—1746)、徐懋德(A.Pereira,1689—1743)推測《歷象考成》預報的月食將會出現“微差”,屆時欽天監實地測驗,果出現“實測與推算分數不合”的現象,遂奏請將《歷象考成》重新修訂,獲得雍正皇帝批準。[7]乾隆二年(公元1737年),協辦吏部尚書顧琮又三次上書,要求對《歷象考成》“盡心考研,增補圖說”[7],所上條陳準奏后,即開始《歷象考成后編》的編撰。乾隆三年(公元1738年),負責修訂歷書的莊親王允祿上奏陳述《后編》的主要優點,將太陽視差與蒙氣差、橢圓模型并列為三大主要改進,其中太陽視差列于首位,文中言道:

《歷象考成》一書,其數惟黃赤大距減少二分,余皆仍《新法算書》西人第谷之書。康熙中西人有噶西尼、法蘭德等,發第谷未盡之義,其大端有三:其一謂太陽地半徑差,舊定為三分,今測袛有十秒。……戴進賢等皆知其說,因未經驗證,不敢遂以為是。[7]

《后編》關于太陽視差最大的改進在于引進了G.D卡西尼(Giovanni Domenico Cassini, 1625—1712)的觀測結果。1672年火星沖日期間,卡西尼在巴黎,其助手里奇(Jean Richer,1630—1696)在法屬圭亞那島同時進行觀測,測得火星視差25秒,進而推測出太陽最大視差為9.5秒,有史以來第一次得到最為接近真實的數據,推翻了當時太陽系大小的觀念,引起了西方學界巨大的興趣,甚至是狂熱。此后,西方天文學家又多次通過觀測火星、金星測算太陽視差,修正日地距離。試圖將“天文學中最崇高的問題”、“丈量宇宙的標準……天文學里至為重要的基礎數值”進一步修正。[8]《后編》編撰時,將其推算方法記錄在內,這也是中國首次將具有現代意義的太陽視差引入官方歷法。

自后噶西尼等謂日天半徑甚遠,無地半徑差,而測量所系只在秒微,又有蒙氣雜乎其內,最為難定。因思日月星之在天,惟恒星無地半徑差,若以日與恒星相較,可得其準。而日星不能兩見,是測日不如測五星也。土木二星在日上,去地猶遠,地半徑差愈微。金水二星雖有時在日下,而其行繞日,逼近日光,均為難測。惟火星繞日而亦繞地,能與太陽沖,故夜半時火星正當子午線。于南北兩處測之,同與一恒星較,其距恒星若相等,則是無地半徑差。若相距不等,即為有地半徑差,其不等之數,即兩處地半徑差之較。且火星沖太陽時,其距地較太陽為近,則太陽地半徑差必更小于火星地半徑差也。[9]

《后編》求太陽視差之法主要分為兩個步驟,其方法如下:

步驟一:求火星地平視差

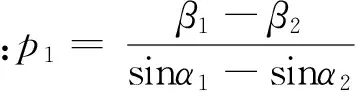
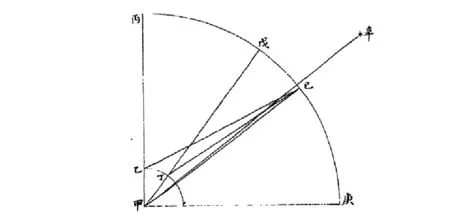
圖6　《后編》中的地平視差Fig.6　The horizontal parallax in "Li Xiang Kao Cheng Hou Bian"

《后編》所用算法與《歷象考成》并不相同,主要是考慮到太陽視差數值較小,利用了sina≈a(當a較小時)簡化計算步驟。書中在此算法之后,又將原始數據按《歷象考成》之法重新計算,二者結果基本相合,借此說明《歷象考成》誤差實源于觀測,而非算法之誤。

步驟二:推算太陽視差

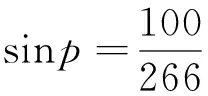
《后編》較為完整的介紹了卡西尼的太陽視差及其計算原理,對于太陽視差有了進一步的認識,僅從理論方面講,已與西方相差不遠。但可惜的是中國天算家對視差的興趣主要在于以交食為中心的歷法編撰方面,對其宇宙結構方面的意義并不重視。奈何太陽視差十分微小,在歷法中基本忽略不計,這也就失去了它在實際計算中的主要價值,致使后續天算家對它的關注度更加低了,至少遠沒有產生類似于西方的影響。

4　結　語

從明末清初西學初始傳入,直到《后編》編撰完成,西方太陽地平視差的核心知識已基本傳入中國。在此過程中,中國天算家主流上對這一內容并不排斥,積極將之引入歷法之中,相關問題的計算精度也有了一定的提高。

縱觀《崇禎歷書》到《后編》等幾部官方歷法中的太陽視差,主要筆墨幾乎都集中在幾何原理、算法、應用等方面,內容較為全面,基本囊括該知識從古典到近代的主要觀點,完全可以滿足中國歷家編歷的需求。可以說在理論知識層面上已與西方相差不遠,但對該內容在修正日地距離、探索宇宙真實結構方面的價值,重視程度尚顯不足,至少未能引起中國歷家的足夠興趣。簡單的說,就是更為注重視差的具體數值、推算方法、太陽視位置的精度，而對于視差在其他方面的意義,則僅限于介紹行星內外順序時的寥寥數語,重視程度不及前者。這一點從莊親王允祿上奏陳述《后編》主要優點,僅言太陽視差從3′變為10″,而對與此緊密相關的日地距離大幅變化卻只字未提,即可見其側重所在。

官方歷書的主要作用是編訂歷法,重視算法與數據是其必然要求,而民間歷算家并無編歷任務,似乎也沒有多少人對視差在宇宙結構方面的意義感興趣。雖有不少著作談及視差,但內容多以歷法計算為主,僅有少數論及其他方面,也幾乎未出官方歷法所限。如熊明遇《格致草》中言:“何為視差?曰:如一人在極西,一人在極東,同一時仰觀七政,則其躔度各不同也。七政愈近人者,差愈大;愈遠者,差愈小。月最大,日次之,熒惑次之,歲星又次之,填星最小幾于無有,故知月最近,填星最遠。”[10]幾乎照搬《崇禎歷書》原文。梅文鼎亦言:“居七政之上,最近大圜最遠于地者為恒星。恒星之下,次為土星……。以視差言之,與人目遠者視差微,近者視差大,故恒星之視差最微,以次漸增,至月而差極大也。”[11]也僅限于重復《崇禎歷書》中視差確定行星順序的作用。除此之外,梅氏談及視差的論述基本集中于確定行星視位置方面。即便在《后編》出版之后,中國天算家已經了解了卡西尼視差觀測的重大意義,此類狀況依然沒有多大改觀,相對于該問題在西方引起的轟動,差別十分明顯。乾嘉時代,一些學者還將視差附會宣夜說,借以論證西學中源。如《宣西通》中言道:“西士視學亦出于宣夜,西法所謂視徑、視行、視差,以為非七政之實,人視之則然。此正旁望黃山俯瞰深谷,青非真色墨非有體之說所觸類而引申也。”[12]此類論點雖非全不合理,但偏重于附會古籍、盲目自大,距離探索宇宙真實結構的精神更加遠了。還有的學者認為天文歷法只要保留其“使人主恐懼修省”社會功能就足夠了,連是否精確也可放在一邊。如《理學逢源》言道:“然古之歷疏而切于國計民生之用,后之歷密而無當于始。……是謂天變為不足畏,而何以動人主恐懼修省之端。”[13]此類學者雖并不占主流,但也映射出一部分學者對自然知識的看法。

總體而言,《后編》出版之后中國天算家事實上已經了解了太陽視差的相關知識以及卡西尼觀測結果帶給宇宙模型的巨大變化,但由于國內意識形態的種種原因,雖接受了這些理論和算法,但僅僅是將其視為歷法計算中的常數系統,缺少對宇宙真實結構方面的科學訴求,是以未能產生類似西方天文學界的影響。

[1]利瑪竇.乾坤體義[M]∥文淵閣四庫全書:子部(第787冊).臺北:臺灣商務印書館,1983:768.

[2]李之藻.渾蓋通憲圖說[M]∥文淵閣四庫全書:子部(第789冊).臺北:臺灣商務印書館,1983:857.

[3]王英明.歷體略[M]∥文淵閣四庫全書:子部(第789冊).臺北:臺灣商務印書館,1983:985.

[4]徐光啟編撰,潘鼐匯編.崇禎歷書·附西洋新法歷書十種[M].上海:上海古籍出版社,2009:43-59.

[5]王萍.西方歷算學之輸入[M].臺北:精華印書館,1980:45-69.

[6]允祿,何國宗,梅瑴成,等.御制歷象考成[M]∥文淵閣四庫全書:子部(第790冊).臺北:臺灣商務印書館,1983:108-119.

[7]趙爾巽.清史稿 [M].北京:中華書局,1991:1670-1671.

[8]龐雪晨.十九世紀金星凌日天象在中西方的反響——從郭嵩燾使英日記切入[J].自然辨證法研究,2014(4):104-110.

[9]梅瑴成,何國宗,戴進賢,等.御制歷象考成后編[M]∥文淵閣四庫全書:子部(第792冊).臺北:臺灣商務印書館,1983:11-17.

[10] 熊明遇.格致草[M]∥薄樹人.中國科學技術典籍通匯·天文卷.鄭州:河南教育出版社,1998:94.

[11] 梅文鼎.歷學疑問(卷二)[M]∥梅瑴成.梅氏叢書輯要.鴻文書局石印本,1887.

[12] 許桂林.宣西通(卷二)[M].清嘉慶刻本.

[13] 汪紱.理學逢源(卷七外篇)[M].清道光十八年敬業堂刻本,1838.

(編輯陳鐿文)

The spread of the solar parallax in China during later Ming and early Qing Dynasty

ZHANG Qi， SONG Zhi-ye

(The Institute for History of Science and Technology, Inner Mongolia Normal University, Hohhot 010022， China)

During later Ming and early Qing Dynasty, this knowledge was introduced into China, and was introduced into the official calendar system. It was systemized and revised to varying degrees from "Chong Zhen Li Shu" to "Li Xiang Kao Cheng Hou Bian". Consequently the knowledge in China on the theoretical level was nearly comparable to that in the West; however, due to the fact that Chinese astronomy centered on the practical functionality, it remained merely a means of obtaining an important parameter in calendar calculation, absent of the kind of influence enjoyed in the West. Through the comparison of several accounts of solar parallax in the official calendar, this paper studies Chinese astronomers′ and mathematicians′ understanding of the development of this knowledge, and analyzes their degrees of understanding of the solar parallax and science demands.

solar parallax; the astronomical unit; the calendar

2015-11-02

國家自然科學基金資助項目(11373016)；國家自然科學基金資助項目(11261036)；內蒙古高等學校科學研究項目(NJSY16036)；內蒙古師范大學博士科研啟動經費項目(2014YJRC027)；內蒙古師范大學科研基金一般項目(2014ZRYB08)

張祺，男，內蒙古呼和浩特人，博士，從事天文學史、科技史研究。

P1-09

A

10.16152/j.cnki.xdxbzr.2016-04-029