某超長剪力墻結構帶部分框支的平面有限元分析和側向剛度研究

林寶新,　趙　杰

(1.安徽建筑大學 土木工程學院,安徽 合肥　230022; 2.安徽建筑大學 建筑設計研究院,安徽 合肥　230022)

?

某超長剪力墻結構帶部分框支的平面有限元分析和側向剛度研究

林寶新1,2,趙杰1

(1.安徽建筑大學 土木工程學院,安徽 合肥230022; 2.安徽建筑大學 建筑設計研究院,安徽 合肥230022)

文章以某帶端部轉換高層剪力墻結構為例,進行了多遇地震下不同力學模型的彈性計算和罕遇地震下的彈塑性分析,對轉換部位側向剛度進行對比研究,并對單榀框支轉換部位構件進行在豎向恒載和水平地震作用下的平面有限元分析,對其應力分布情況進行了探討。結果表明,結構整體和轉換部位具有較好的承載和變形能力,可供同類工程參考。

框支剪力墻;剛度比;平面有限元分析;靜力彈塑性分析

為了滿足人們對下部大空間、上部小空間的建筑功能要求,現代工程中廣泛采用帶部分框支轉換的高層建筑。但這種結構在轉換處往往上部承托剛度較大的剪力墻,下部布置剛度較小的框支柱和少量剪力墻,使得轉換部位附近的側向剛度發生突變,地震作用下容易發展成薄弱層,所以設計中需注意對轉換部位的剛度進行校核;同時由于豎向抗側力構件不連續,造成豎向荷載的傳力不直接,轉換部位受力復雜,需對其進行詳細的應力分析。

國內外對平面規則性結構研究較多,但對超長且端部轉換易產生扭轉的平面不規則結構研究較少,本文采用多種計算模型對結構整體和部分分別計算側向剛度進行復核。文獻[1-4]分析表明框支梁及上一層墻體應力復雜,本文針對受力復雜的框支構件,采用平面有限元法分析了不同工況下框支構件的應力分布情況,按應力分析結果取最不利值校核配筋,并且補充了大震下的抗震性能評估。

1　工程概況、抗震目標及結構不規則性

合肥濱湖某小區18#住宅樓,采用剪力墻結構,地下1層,地上29層,嵌固端設于地下室頂板。建筑高度84.55 m,建筑西端部在2層商業頂存在局部轉換,轉換的墻體面積占10%,轉換層在⑦軸附近存在錯層[5];商業一層建筑層高4.5 m,二層建筑層高4.2 m,商業二層頂與住宅三層頂平,住宅標準層層高2.9 m。

轉換層平面布置如圖1所示,②軸框支部分剖面如圖2所示。

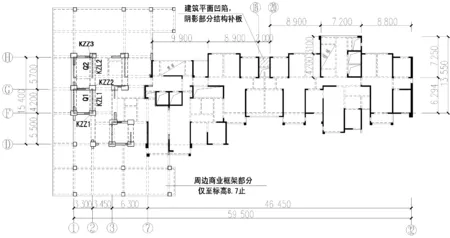
圖1　轉換層平面布置圖

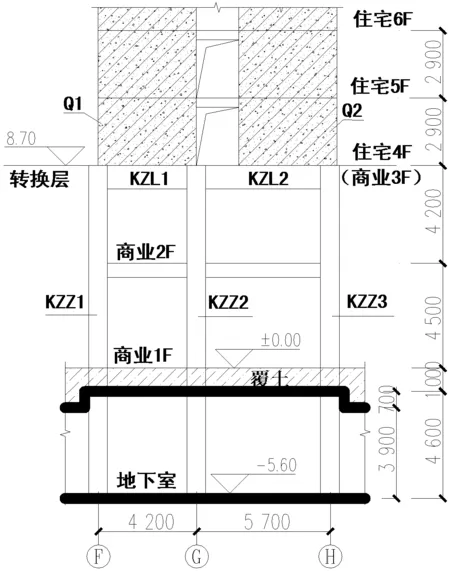
圖2　②軸局部剖面圖

框支梁KZL1、KZL2截面為900 mm×1 000 mm,框支柱KZZ1、KZZ2、KZZ3截面為1 100 mm×800 mm。

該工程安全等級為二級,抗震設防類別為丙類,抗震設防烈度為7度,設計基本地震加速度值0.1g,場地類別Ⅱ類,設計地震分組為第1組,結構抗震等級在框支轉換處及局部錯層處為一級,其他部位抗震等級均為二級。抗震性能目標見表1所列。根據“三水準兩階段”的抗震設防原則,結合建筑性能化抗震設計的概念,選用D級的抗震性能目標[6],其中框支梁柱、轉換梁上一層剪力墻及底部加強區剪力墻按“關鍵構件”設計[6]。

表1　抗震性能目標

注:括號中數字為性能水準。

本工程存在4項不規則類型,簡要概述如下:

(1) 扭轉不規則。轉換部位在建筑物端部,扭轉問題突出;結構超長(縱向L=59.5 m),按文獻[7]考慮質心與剛心5%L偏心距產生的扭轉難以避免,計算表明在規定水平力作用下,考慮偶然偏心的扭轉位移比大于1.2。

(3) 樓板不連續。商業與住宅交接部位存在錯層。

(4) 構件間斷。存在部分框支轉換,豎向抗側力構件不連續。

因此,本工程屬于特別不規則結構,為超限高層建筑[8]。

2　多遇地震下的振型分解反應譜分析

2.1結構整體分析

本文采用2種力學模型對結構進行整體分析，分別為:① 基于空間桿-墻元模型的SATWE程序,作為主要計算程序；② 基于廣義協調墻元模型的PMSAP程序,作為補充計算程序。

本工程采用剛性樓板假定,轉換層下按3層建模,標準層凹陷部位補設板帶按有拉板模型計算,考慮偶然偏心和雙向地震作用,連梁折減系數為0.7,結構阻尼比5%,主要計算結果見表2所列。

因為PMSAP基于廣義協調理論的子結構墻元模型與SATWE中基于經典協調模式的墻元模型有差異,所以2種計算程序結果中剛度比差別較大,但均滿足規范要求。計算結果表明:樓層豎向構件最大位移比小于1.4,樓層最大層間位移角小于1/1 000,結構具有合適的剛度;僅X向樓層剪重比小于1.6%的樓層數不超過4層,且

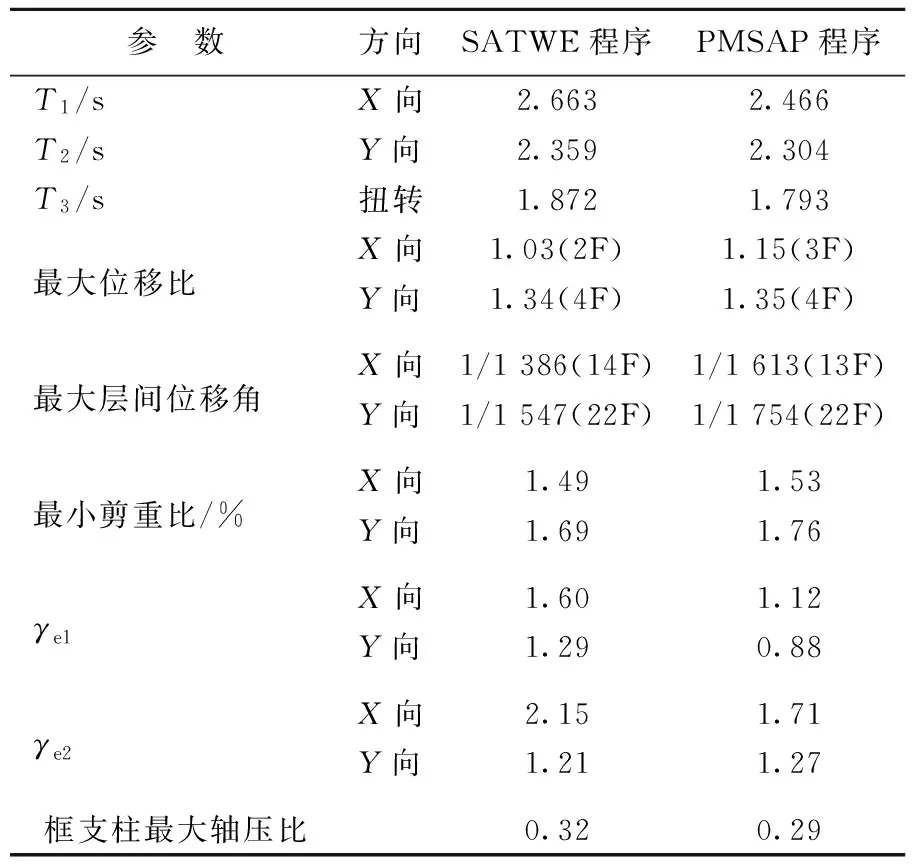
表2　多遇地震彈性計算結果

注:T1、T2、T3為基本自振周期;γe1為轉換層與相鄰上

層剛度比;γe2為轉換層下、上部結構等效剛度比。

經剪力調整后最小剪重比均大于1.6%;轉換層與相鄰上層剛度比γe1不小于0.6,轉換層下部結構與上部結構等效剛度比γe2不小于0.8;框支柱軸壓比最大值小于0.6。該結構可以保證“小震不壞”的抗震設防目標。

2.2轉換部位作為隔離體的側向剛度計算

本工程的轉換部位在建筑的端部,考慮該結構縱向較長,且轉換樓板處存在樓梯洞口,轉換層下在⑦軸附近有局部錯層,受力復雜,需分析水平剪力能否有效傳遞。忽略周邊商業框架部分,① ～⑦軸轉換部位對應的上、下層平面布置如圖3所示。

為避免帶局部錯層的結構端部轉換在地震作用下的傳遞途徑不能有效進行,根據圣維南原理,取最不利模型:對圖1的① ～⑦ 軸建筑結構取隔

圖3　① ～⑦軸平面布置圖

離體,采用SATWE單獨建模計算,隔離體模型在轉換層下按2層建模,底部仍嵌固于地下室頂板,豎向構件在⑦軸附近不存在錯層。

隔離單體計算結果表明:轉換層與相鄰上層剛度比γe1在X方向為2.31,在Y方向為0.96,均不小于0.6,滿足文獻[6]要求;根據文獻[6]附錄E.0.1條規定,采用剪切剛度比算法驗算轉換層與相鄰上層剛度比γe1在X方向為2.24,在Y方向為0.65,均大于0.5,滿足規范要求。

3　多遇地震下的彈性時程分析

選取業主單位提供的3條地震波進行多遇地震作用下整體結構的補充分析,所選取的地震波加速度時程曲線如圖4所示。

圖4　地震波加速度時程曲線

將地震波的有效峰值調整為35 cm/s2,所選地震波的持續時間大于文獻[7]規定的15 s和5T1的最大值,按雙向地震輸入,并分別沿X向和Y向加載,主次方向峰值加速度比例為1∶0.85,阻尼比為0.05,特征周期0.35 s;3條人工波user1、user2、user3的地震影響系數曲線與振型分解反應譜法所用的曲線,不僅結構在第1～3振型周期點上,而且在第4～6振型周期點上相差均小于20%,符合統計意義上“相符”的要求[7]。

基底剪力計算結果見表3所列,每條地震波作用下的結構基底剪力均大于規范反應譜法計算結果的65%,且3條波的基底剪力平均值大于規范反應譜法計算結果的80%,所選地震波滿足文獻[7]中5.1.2條對所選地震波的規定。

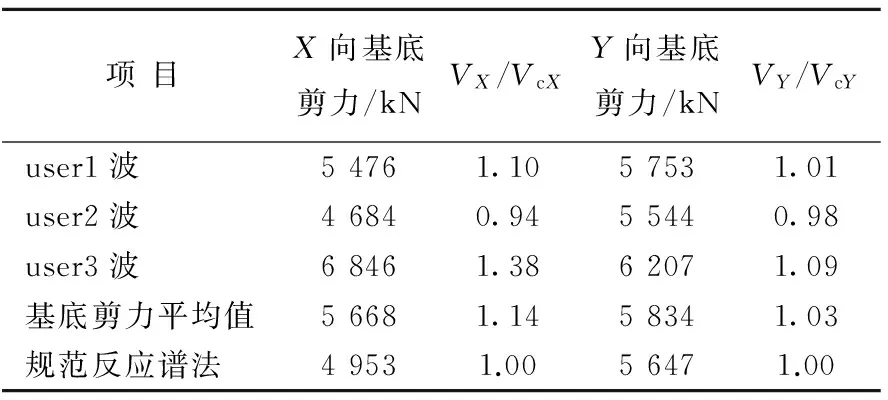
表3　時程分析法與反應譜法基底剪力比較

注:VX/VcX、VY/VcY為各地震波基底剪力及3條波基底剪力平均值相對于規范反應譜計算結果的比值。

主方向層間位移角和樓層剪力包絡圖分別如圖5、圖6所示,各地震波在X、Y向層間位移角最大值分別為1/1 415、1/1 568,滿足規范要求。實際設計中選用時程分析法的包絡值和振型分解反應譜法的較大值進行設計。CQC法即完全二次振型組合(complete quadratic combination)方法。

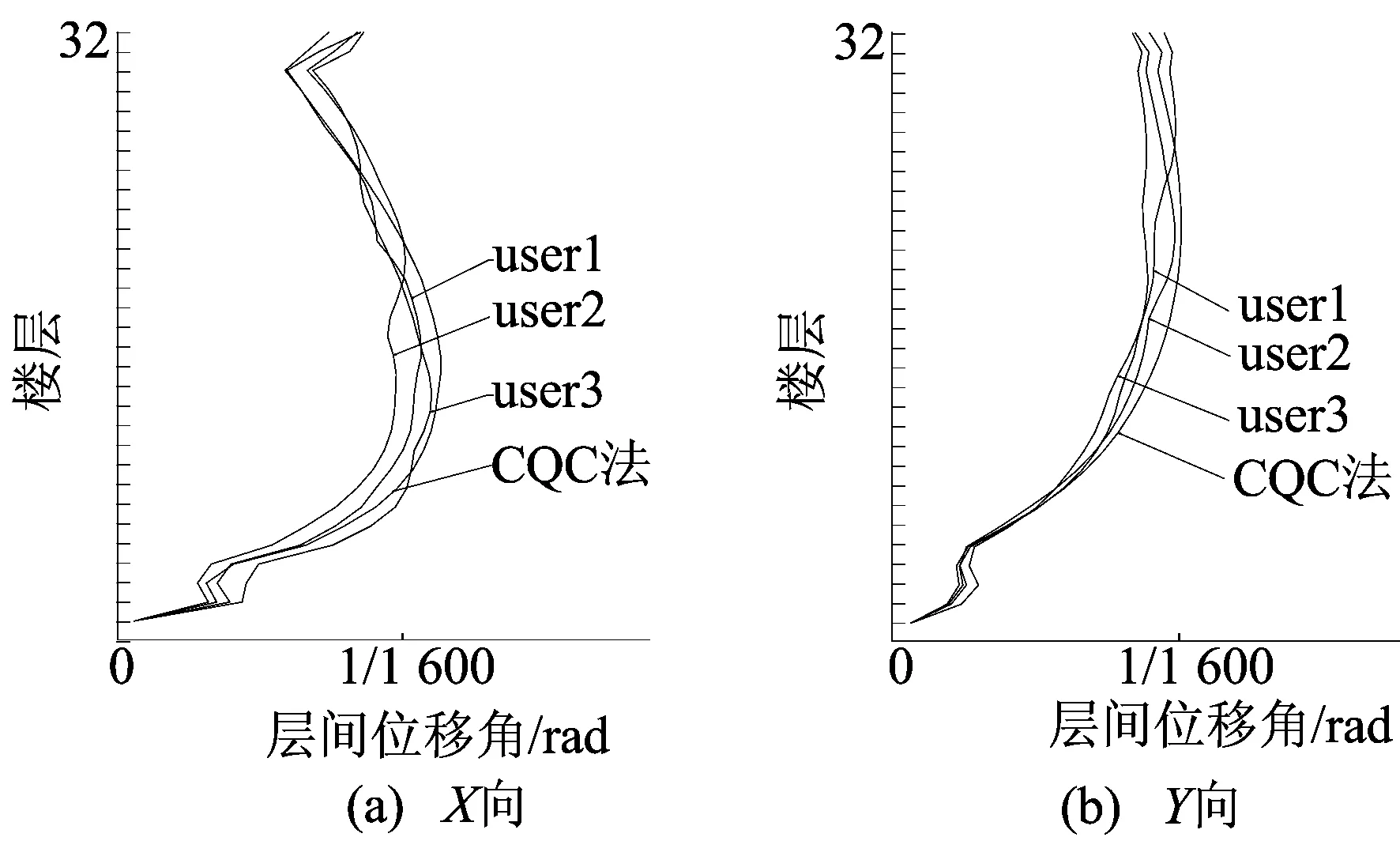
圖5　主方向層間位移角

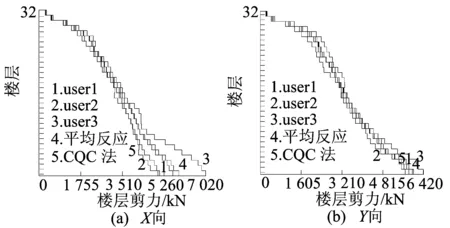
圖6　主方向樓層剪力包絡圖

4　框支部分的平面有限元分析

文獻[6]10.1.5條規定：“復雜高層建筑結構中的受力復雜部位，尚宜進行應力分析，并按應力進行配筋設計校核”。為研究框支層附近構件的受力情況,采用高精度有限元軟件FEQ對圖1的②軸框支梁、框支柱和轉換層上部2層剪力墻進行平面有限元分析[9],結構離散化,采用三角形單元,單元控制長度取400 mm,考慮了地震力、風荷載及豎向荷載作用下,恒載簡圖如圖7所示,小震、中震彈性下配筋簡圖如圖8、圖9所示。

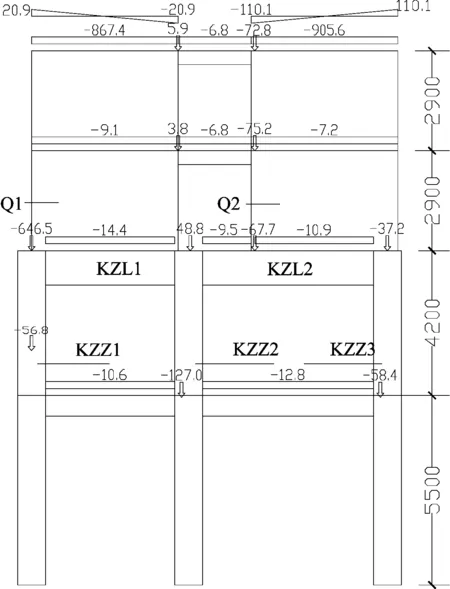
圖7　恒載簡圖

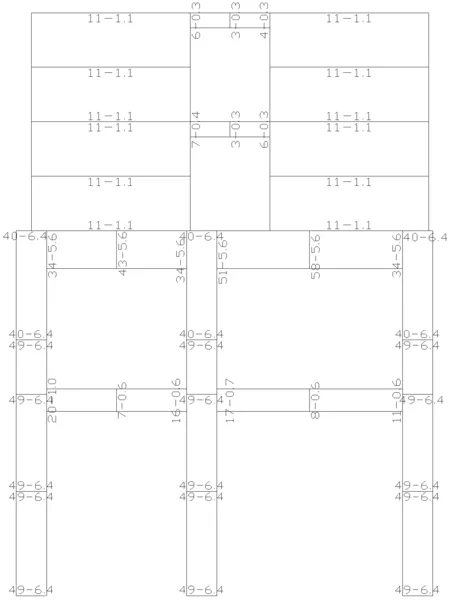
圖8　小震下配筋簡圖(As-Asv)

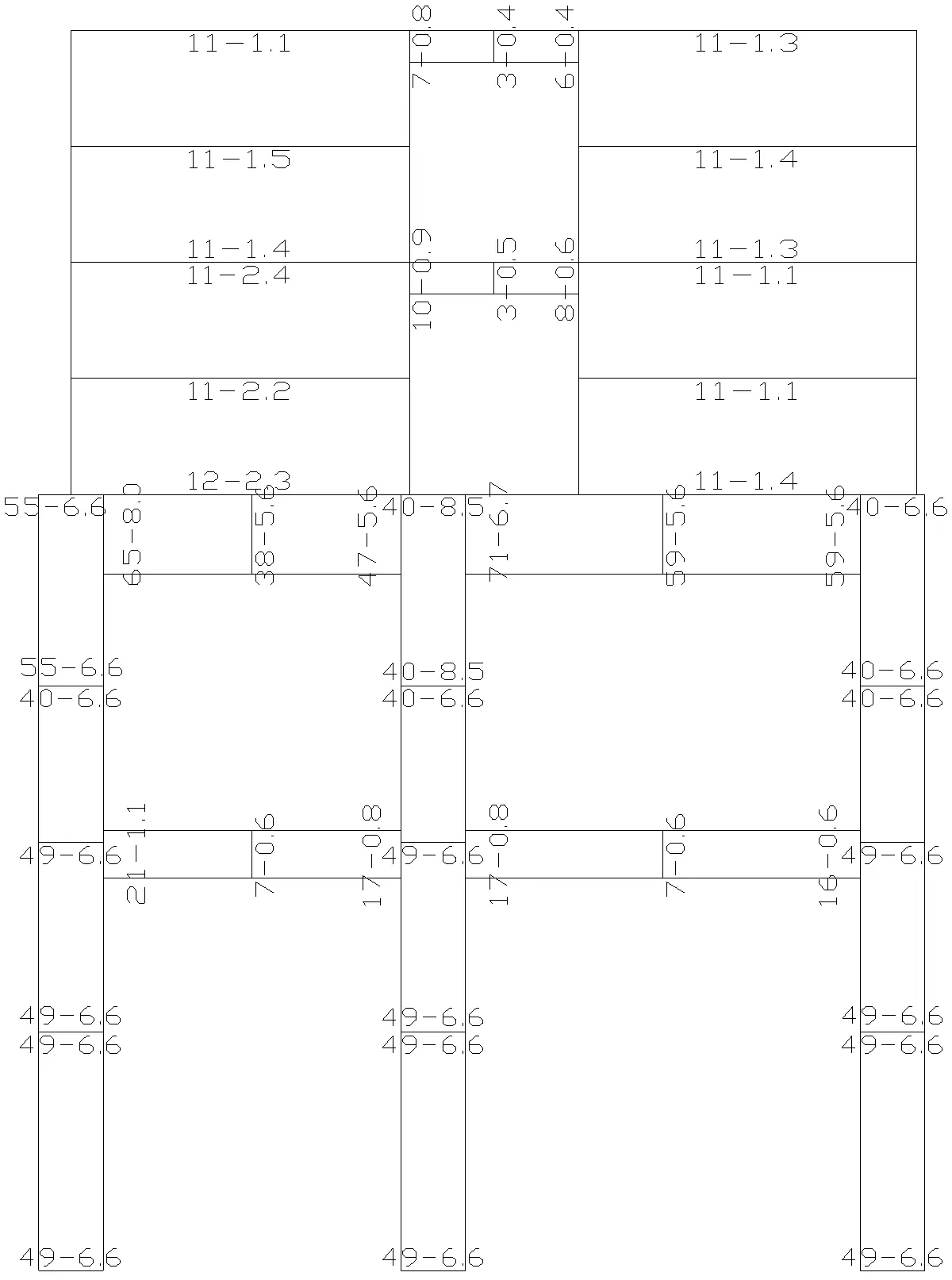
圖9　中震彈性下配筋簡圖(As-Asv)

設計時偏于安全地選取FEQ計算結果與SATWE整體計算結果的較大值進行配筋。

圖8、圖9中,As為主筋面積,柱為一端的面積,墻為一端的面積,梁為一受拉邊的面積,單位為cm2;Asv為箍筋面積,對墻為水平分布筋的配筋面積,單位為cm2。

豎向恒載下SATWE與FEQ計算框支梁內力對比見表4所列。由表4可知,恒載工況下,與SATWE整體計算結果相比,FEQ計算結果中框支梁彎矩明顯減小,但梁端剪力增大。可見SATWE分析計算時未考慮框支梁與上部墻體的共同作用,FEQ計算結果體現了墻梁共同作用、豎向傳力拱的影響和框支梁偏拉構件的特點。此外，FEQ計算結果中框支梁軸力偏大,SATWE計算結果顯示,當轉換層采用剛性樓板假定時,框支梁的軸力為0,當轉換層采用彈性膜假定時,KZL1、KZL2的軸力分別為274、340 kN。

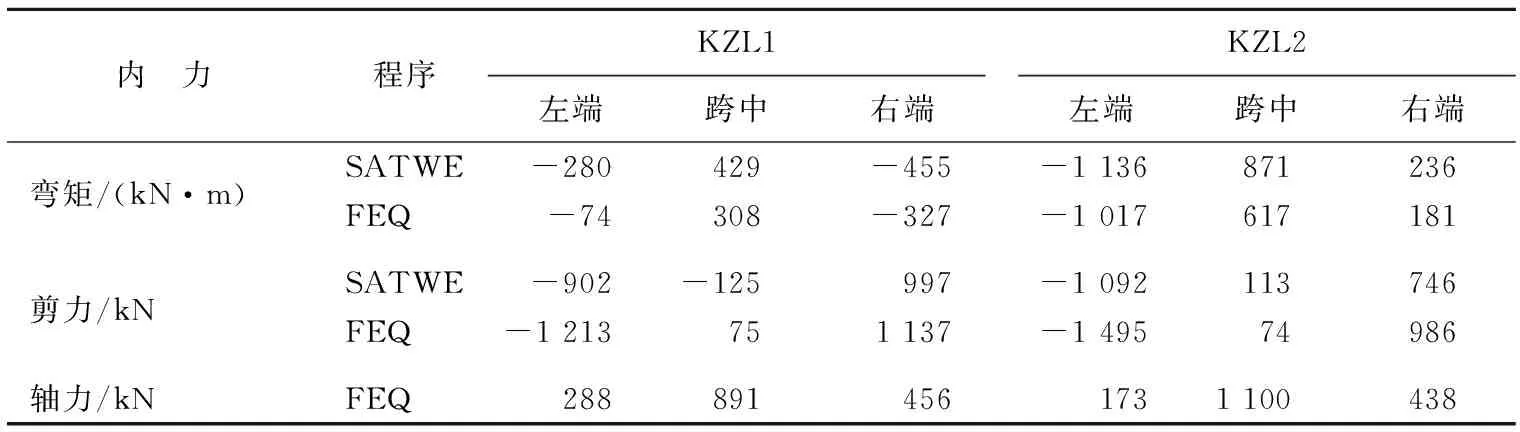
表4　豎向恒載下SATWE與FEQ計算框支梁內力對比

4.1豎向荷載作用下的受力特點

豎向恒載作用下應力分布曲線如圖10所示。

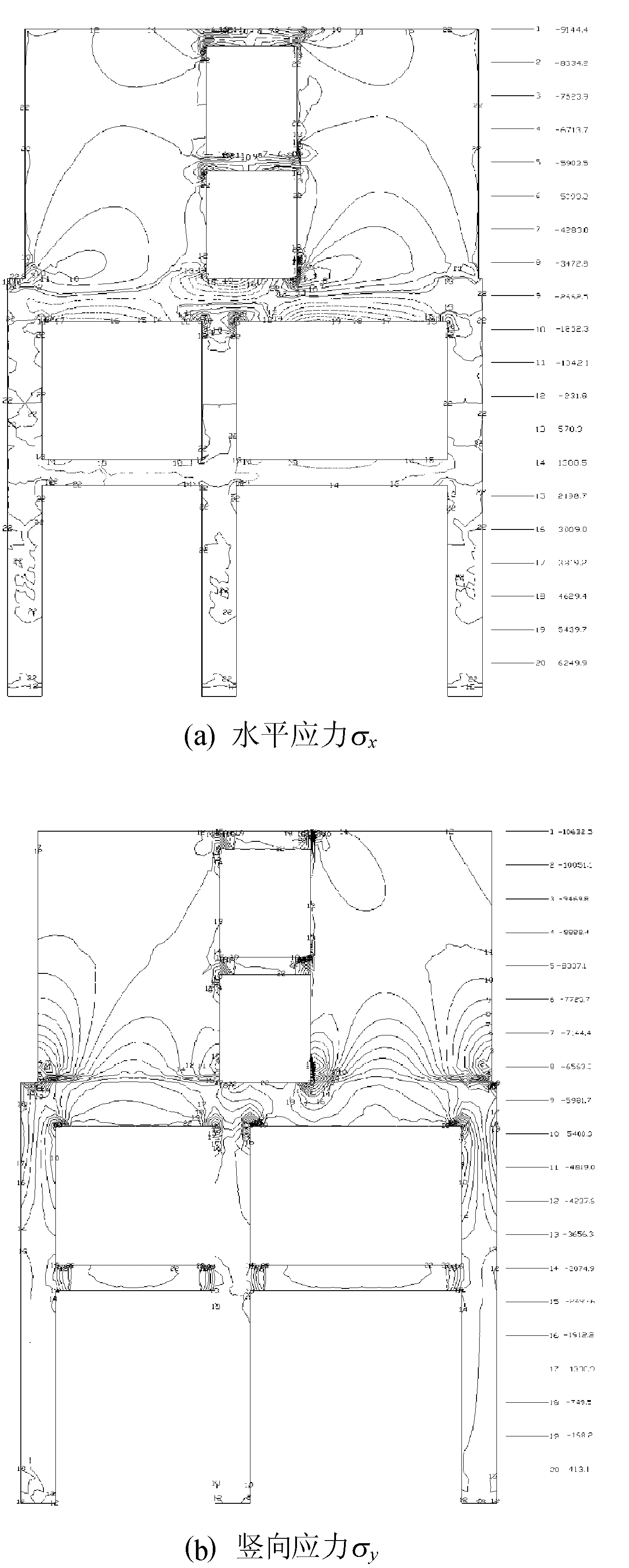
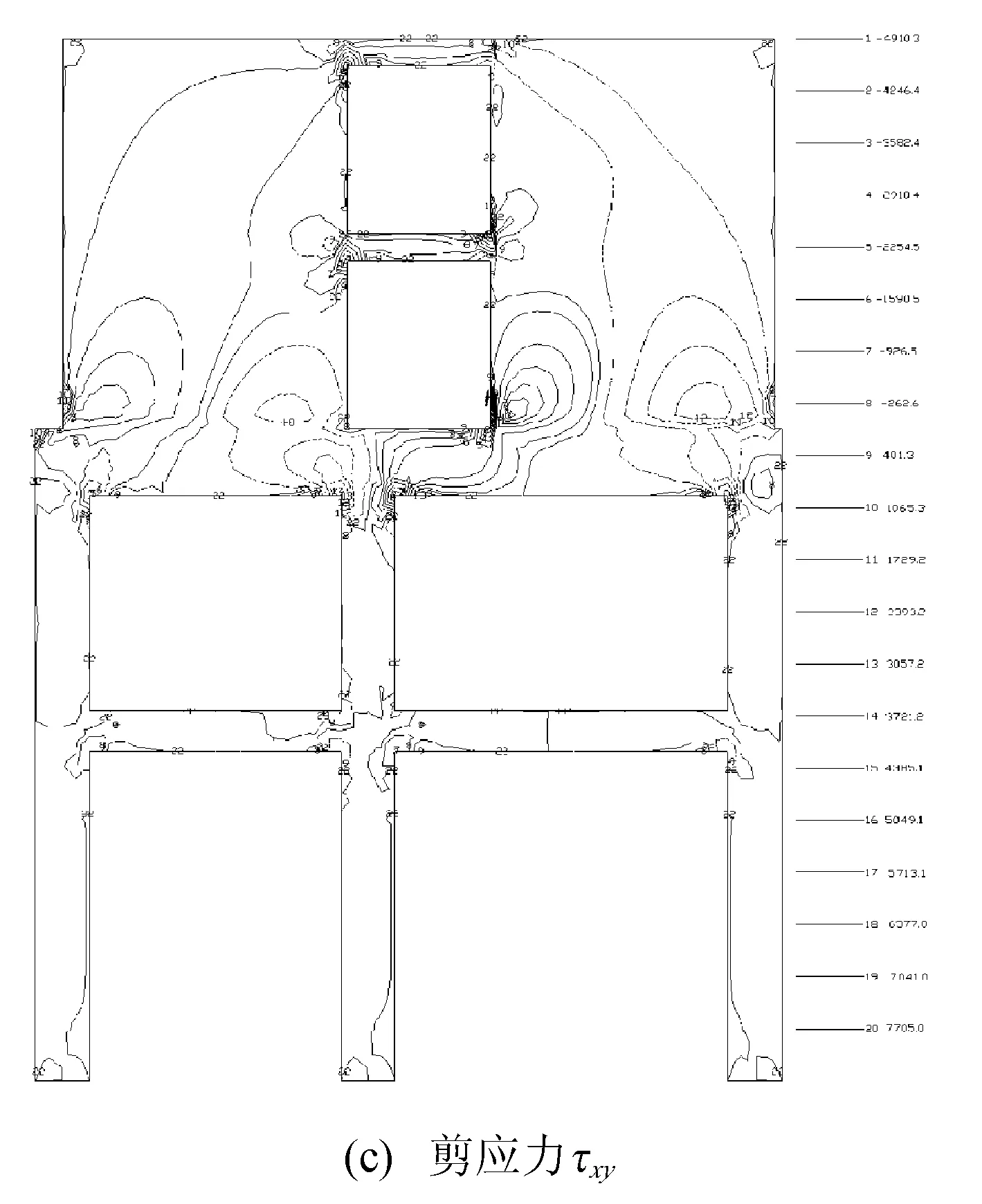
圖10　恒載作用下的應力分布曲線

圖10中負值實線為壓應力,正值虛線為拉應力,線號22表示“0”應力線。

(1) 水平應力σx分布特點。墻內水平壓應力主要分布在高度L0(框支梁凈跨)范圍內的墻體中,從上到下增大,對于更高的部位，水平應力[1]接近于0。墻肢底部和框支梁交界處存在明顯的壓應力,由于傳力拱的作用,邊柱上方最大應力達到-1.8～-3.4 MPa,可達到(0.4～0.7)q/bw(q為上部結構傳遞至住宅6F的均布荷載,bw為剪力墻厚度200mm),在連梁節點域和Q2靠近框支梁的洞口處存在顯著的壓應力集中,中柱上方存在局部的拉應力區(0.5～3.8MPa),可達到(0.1～0.8)q/bw;墻體所在區域下的梁跨中下邊緣拉應力達到上邊緣壓應力的1.5～2.0倍,框支梁表現出偏心受拉的性質,靠近中柱的梁截面下部出現較明顯的壓應力(-1.8～-7.5MPa),達到(0.4～1.7)q/bw,表現出偏心受壓的性質[2]。

(2) 豎向應力σy分布特點。底部框架對墻肢豎向應力σy的影響大約在梁跨度L0高度范圍內,更高部分基本均勻分布。由于傳力拱的作用,墻肢壓應力由內向外增大,在框支梁端部框支柱上方墻體處應力集中(-6.5～-9.4MPa),達到(1.4～2.1)q/bw,設計時應對墻體兩端底部進行局部抗壓承載力驗算[3];梁跨中的豎向應力很小,也出現由內向外增大的性質,在節點域和Q2洞口邊緣處的梁截面豎向應力最大達到-1.9～-7.7MPa,可達到1.7q/bw,洞口處梁截面豎向應力很小,幾乎為0。

(3) 剪應力τxy分布特點。墻內剪應力呈對稱分布,大約在高度L0墻體范圍內,由上到下增大,在墻肢端部與框支梁交界處剪應力最大達到-1.5～-3.5MPa,可達(0.3～0.8)q/bw;墻下梁跨中剪應力很小,由跨中向兩端增大,在節點域和Q2墻肢左端無墻部分的梁截面剪應力最大達到-1.6～-4.2MPa,可達(0.3～0.9)q/bw,設計時應注意驗算KZL2左端無墻部分的抗剪承載力[3]。

4.2水平荷載作用下的受力特點

Y向地震作用下的應力分布曲線圖如圖11所示,其中負值實線為壓應力,正值虛線為拉應力,線號22表示“0”應力線。

(1) 水平應力σx分布特點。墻肢一側受拉(0.3～1.9MPa),達到(0.06～0.4)q/bw;另一側受壓(-0.4～-2.7MPa),達到(0.08～0.6)q/bw。呈反對稱分布的特點,連梁節點域存在水平應力突變,兩端在頂、底有較大的一拉一壓的水平應力。

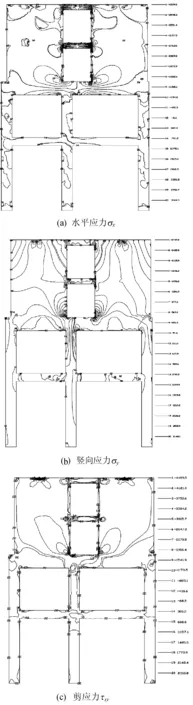
圖11　Y向地震作用下的應力分布曲線

(2) 豎向應力σy分布特點。2片墻分別在洞口邊緣處產生了較大的豎向拉壓應力,Q1受拉(0.3～2.5MPa),達到(0.06～0.5)q/bw;Q2受壓(-0.2～-2.4MPa),達到(0.04～0.5)q/bw。

(3) 剪應力τxy分布特點。墻肢中的剪應力由外向內增大,洞口周圍剪應力較大(-0.4～-1.5MPa),達到(0.08～0.3)q/bw。

水平力作用下,框支梁的應力分布形式與普通框架梁接近,文獻[4]中框支梁也出現相似的應力分布,在節點域內受力復雜,水平應力σx、豎向應力σy、剪應力τxy均較大。

4.3框支剪力墻設計探討

由于框支梁與上部剪力墻協同受力的特性和豎向傳力拱的影響,框支梁跨中的彎矩會比不考慮上部剪力墻作用時要小。當框支梁剛度或上部承托剪力墻布置發生變化時,由于框支梁與上部墻體的共同協調作用,框支梁內力會發生相應的變化。選取圖2中框支梁KZL1、KZL2,在恒載作用下,通過FEQ平面有限元進一步分析。

(1) 不改變框支梁的截面尺寸,調整墻體布置。當框支梁上層剪力墻滿跨布置時,計算表明:KZL1、KZL2沿梁跨全長彎矩、剪力、軸拉力均減小,框支梁與上部剪力墻的共同工作能力增強,對框支梁的受力有利。

(2) 不改變剪力墻的布置,調整框支梁剛度。將框支梁截面尺寸由900 mm×1 000 mm改為1 000 mm×1 200 mm,計算表明:當框支梁剛度增大時,KZL1、KZL2沿梁跨全長彎矩、剪力均增大,框支梁與上部剪力墻的共同工作能力受到削弱,框支梁分擔的荷載相應增大[10],截面配筋相應增加;同時框支梁的剛度增大容易造成“強梁弱柱”的破壞機制,不利于抗震,所以框支梁剛度不宜過大。但由于受抗剪承載力要求的限制[9],截面尺寸也不宜過小。由矩形梁的慣性矩公式I=bh3/12可知,在彈性模量相等的情況下,增加梁高比增加梁寬度對剛度的貢獻大很多。因此,在滿足框支梁強度和剛度的條件下,適當增加截面寬度、減小高度,這樣既可以滿足承載力要求,提高結構延性,有利于抗震,又可以加大轉換層梁下凈高,更好地滿足空間要求。綜合考慮,本工程設計框支梁截面900 mm×1 000 mm是較為合理的選擇。

5　結構靜力彈塑性分析

文獻[7]3.6.2條規定:“不規則且具有明顯薄弱部位可能導致重大地震破壞的建筑結構,應進行罕遇地震作用下的彈塑性變形分析”。為進一步研究框支梁柱在大震下的抗震性能,采用靜力彈塑性分析程序Pushover對結構做罕遇地震作用下的彈塑性變形分析。計算模型中,梁柱采用纖維束模型,剪力墻采用非線性殼單元[11];材料本構關系中,鋼筋采用雙折線模型,混凝土采用單軸應力-應變模型[11]。

初始荷載采用重力荷載代表值,水平加載模式選擇倒三角荷載,停機位移取結構高度的1/20,桿件鉸截面剛度破壞程度指數和墻高斯點破壞比例均取0.7,全樓鋼筋放大系數取1.15,考慮梁柱交接剛域,采用剛性樓板假定。

5.1結構整體抗震性能評估

結構X、Y向的能力曲線、需求曲線和抗倒塌驗算結果如圖12所示(橫軸T為等效單自由度體系周期),能力曲線與需求曲線存在交點,即性能點,能力譜在經過性能點后仍有上升趨勢。性能點時X向頂點位移為191 mm,基底剪力為24 008 kN,為小震彈性時基底剪力的4.8倍,剪重比為7.22%;Y向頂點位移為176 mm,底部剪力為22 934 kN,為小震彈性時基底剪力的4.1倍,剪重比為6.86%。性能點處X、Y向層間位移角分別為1/350(20步)和1/431(24步),均小于彈塑性位移角限值1/140,結構整體抗震性能滿足“大震不倒”的設防目標。

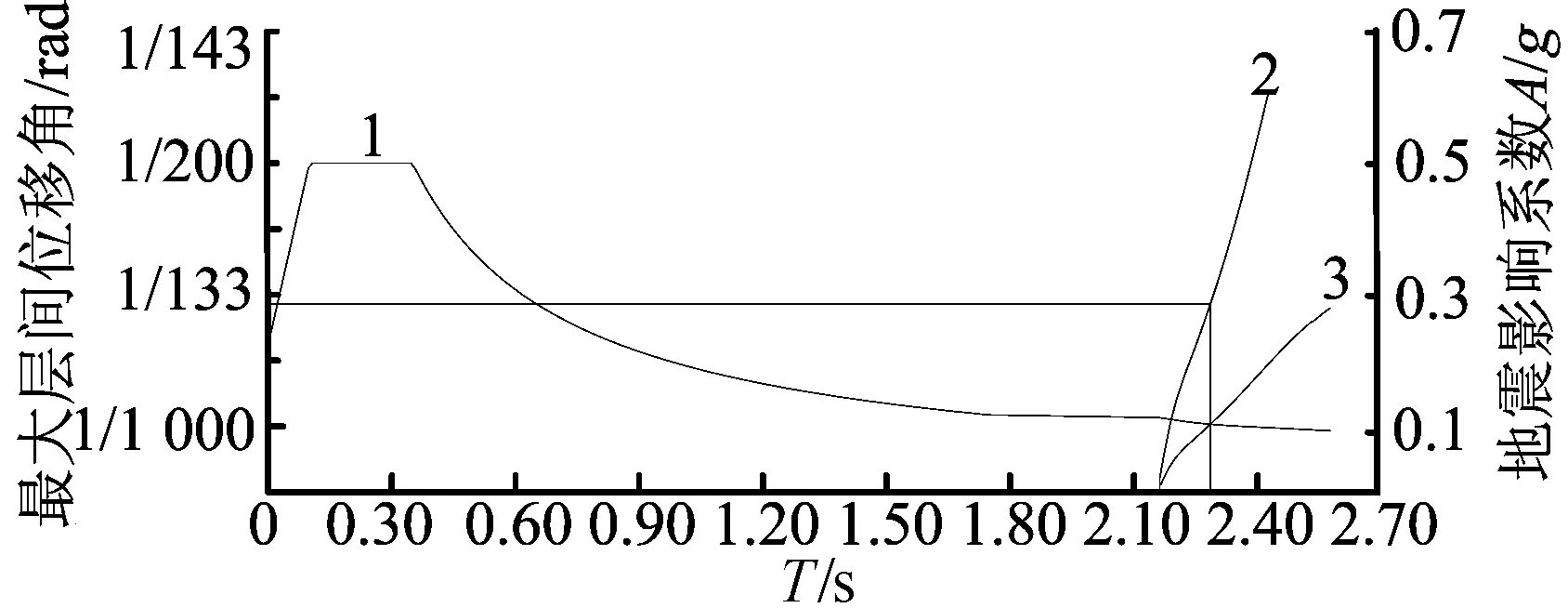
(a)　X向

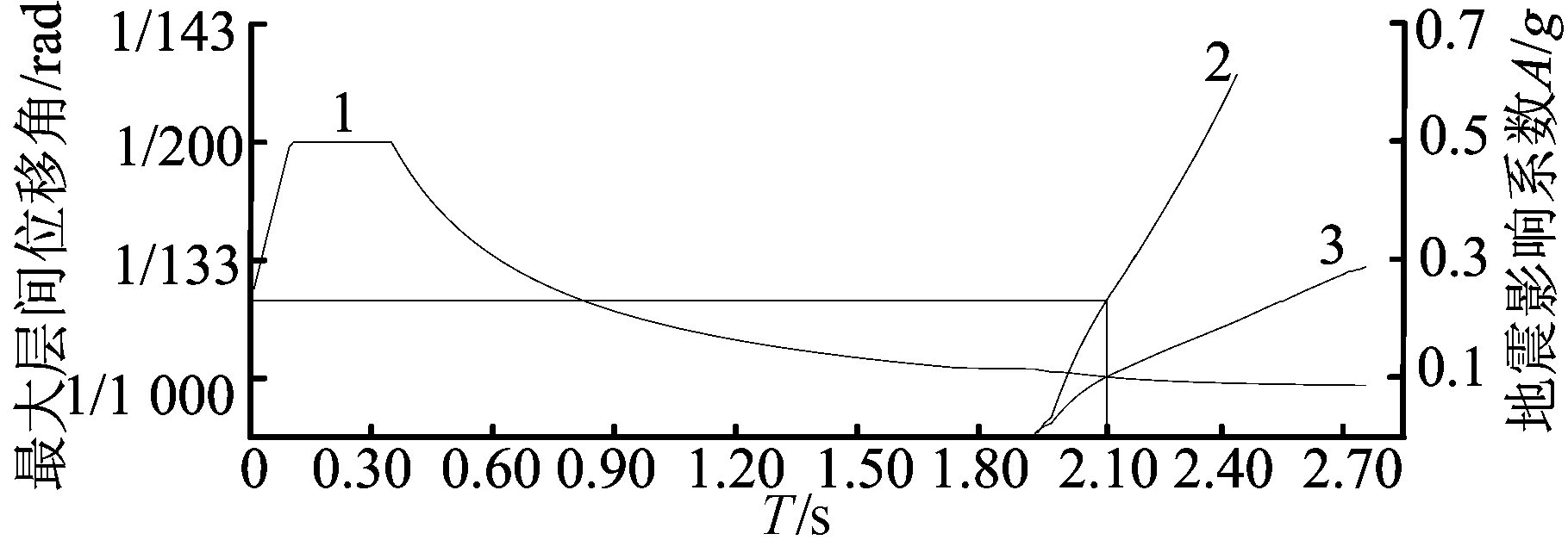
(b)　Y向

5.2結構構件抗震性能評估

推覆結果顯示,連梁作為耗能構件在第11加載步率先開始出鉸,隨著加載步的增加,連梁普遍出鉸,少量框梁也出現塑性鉸,且框梁普遍晚于連梁進入屈服狀態,所有框柱未出鉸。轉換層在性能點處塑性鉸分布如圖13所示,由圖13可以看出,底部少量剪力墻出現水平裂縫和剛度退化,框支梁柱均未出鉸,轉換結構具有良好的抗震性能。

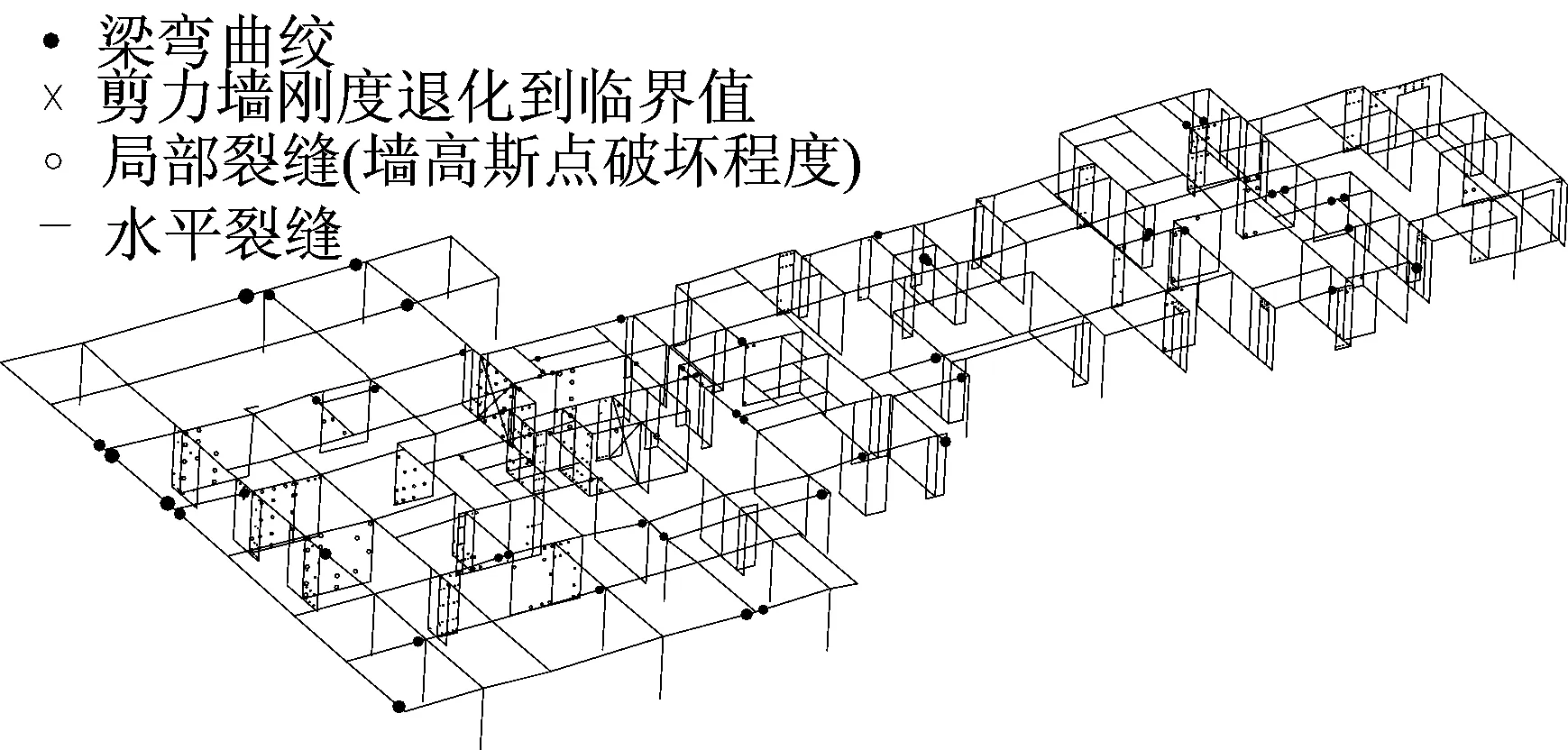
(a)　X向

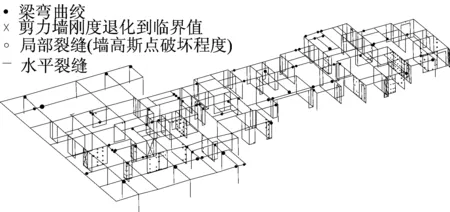
(b)　Y向

6　結構抗震加強措施

通過計算分析,為了滿足抗震性能目標,本工程結構設計中采用以下加強措施:

(1) 框支梁柱按照小震、中震彈性雙控設計。

(2) 框支梁及上一層墻體應力集中,墻內非構造配筋,需按FEQ平面有限元分析結果與整體分析結果的較大值進行設計。

(3) 為了提高框支柱的延性,框支柱軸壓比控制在0.6以下;框支梁柱及剪力墻底部加強區抗震等級提高1級并加強配筋。

(4) 框支梁上部剪力墻若滿跨布置更好,使框支梁與上部墻體形成深梁,提高其共同作用能力。設置剪力墻底部加強區至轉換層及以上2層,剪力墻底部加強部位墻體水平和豎向分布鋼筋配筋率不小于0.3%;適當增加落地墻厚度,以避免轉換層剛度突變。

(5) 框支轉換層樓板厚度取180 mm,雙層雙向配筋,配筋率不小于0.25%,以保證水平力有效傳遞[8]。

7　結　　論

(1) 在多遇地震作用下,振型分解反應譜分析與彈性時程分析結果表明,各項指標滿足規范要求,結構整體能夠滿足“小震不壞”的設防水準。

(2) 框支部分在整體、部分的側向剛度計算結果均滿足規范要求,沒有形成薄弱層。

(3) 通過對單榀框支剪力墻進行平面有限元分析,了解轉換構件的應力分布情況并找出應力集中部位,按應力分析結果校核配筋。

(4) 若框支梁上部剪力墻滿跨布置,框支梁和承托剪力墻的共同作用程度相應增強,對框支梁受力有利。框支梁應有合適的剛度,以改善并盡量形成強柱弱梁的屈服機制。

(5) 在罕遇地震下,彈塑性分析結果表明結構最大層間位移角滿足規范要求的限值,轉換構件沒有發生破壞,結構具有較好的抗震能力。

[1]魏文杰.框支剪力墻結構的彈性靜力分析[D].成都:西南交通大學,2008.

[2]趙西安.鋼筋混凝土高層建筑結構設計[M].北京:中國建筑工業出版社,1992:322-325.

[3]魏璉,王森.轉換梁上部墻體受力特點及設計計算方法的研究[J].建筑結構,2011,31(11):3-6.

[4]林寶新,許加義，李躍.某高層剪力墻帶框支部分靜力彈性和彈塑性分析[J].安徽建筑大學學報,2015,23(3):6-12.

[5]李躍,林寶新,陳明.某帶錯層高層剪力墻結構的抗震性能分析[J].安徽建筑大學學報,2015,23(2):23-29.

[6]中華人民共和國住房和城鄉建設部.高層建筑混凝土結構技術規程:JGJ 3—2010[S].北京：中國建筑工業出版社，2010：15-43.

[7]中華人民共和國住房和城鄉建設部.建筑抗震設計規范:GB 50011—2010 [S].北京：中國建筑工業出版社，2010：31-48.

[8]中華人民共和國住房和城鄉建設部.超限高層建筑工程抗震設防專項審查技術要點[Z].北京:中華人民共和國住房和城鄉建設部,2010.

[9]中國建筑科學研究院PKPM CAD工程部.高精度平面有限元框支剪力墻計算及配筋軟件FEQ [Z].北京:中國建筑科學研究院PKPM CAD工程部,2010.

[10]唐純能,熊源州.轉換梁剛度對框支剪力墻的受力影響[J].建筑與結構設計,2011(11):45-47，50.

[11]中國建筑科學研究院PKPM CAD工程部.PUSH & EPDA 多層及高層建筑結構彈塑性靜力、動力分析軟件用戶手冊[Z].北京:中國建筑科學研究院PKPM CAD工程部,2010.

(責任編輯張淑艷)

Plane finite element analysis and lateral stiffness study of a long partial frame-supported shear wall structure

LIN Baoxin1,2,ZHAO Jie1

(1.School of Civil Engineering， Anhui Jianzhu University, Hefei 230022, China; 2.Institute of Architectural Design and Research, Anhui Jianzhu University, Hefei 230022, China)

Taking a high-rise shear wall structure with end transformation as an example, the elastic calculation in different mechanical models under frequent earthquake and the elasto-plastic analysis under rare earthquake are performed, and the contrastive study of the lateral stiffness of the transformation site is made. Then the plane finite element analysis of the single cross component of the transformation part under vertical constant load and horizontal seismic force is carried out, and the stress distribution of it is discussed. The results show that the whole structure and the transformation part have good bearing and deformation capacities. The study can provide a reference for similar projects.Key words:frame-supported shear wall; stiffness ratio; plane finite element analysis; static elasto-plastic analysis

2015-12-30；

2016-03-31

安徽省科技攻關計劃資助項目(1501041133)

林寶新(1966-),男,安徽和縣人,安徽建筑大學教授級高工,碩士生導師.

10.3969/j.issn.1003-5060.2016.07.021

TU375.1

A

1003-5060(2016)07-0970-09