加權(quán)無窮序列空間上集合的列緊性

趙文強, 張一進

(1. 重慶工商大學數(shù)學與統(tǒng)計學院, 重慶　400067; 2. 重慶郵電大學理學院, 重慶　400065)

?

加權(quán)無窮序列空間上集合的列緊性

趙文強1, 張一進2

(1. 重慶工商大學數(shù)學與統(tǒng)計學院, 重慶400067; 2. 重慶郵電大學理學院, 重慶400065)

加權(quán)無窮序列空間lp(φ)是通常lp空間的推廣.本文考慮其集合緊性問題，證明了當p≥2時,M?lp(φ)為列緊集的充要條件是M一致有界且具有某種意義上的一致收斂性.這一結(jié)果豐富了泛函分析的內(nèi)容.

加權(quán)無窮序列空間;緊集;ε-網(wǎng);一致有界;一致收斂

緊性概念是泛函分析中一個基本且重要的內(nèi)容[1-4],應用于現(xiàn)代分析學的多個領(lǐng)域,如偏微分方程的穩(wěn)定性等問題.因此,對于一些具體距離空間上集合的緊性問題進行探討,對準確把握緊性的概念及其應用是有裨益的.文獻[5]討論了特殊無窮序列空間l2和c0上的有界線性算子的矩陣表示,文獻[6]研究了序列空間的有界逼近性質(zhì)和緊逼近性質(zhì).我們考慮具有權(quán)數(shù)的無窮序列空間lp(φ)(p>0)上的集合緊性問題.

設(shè)φ是定義在實數(shù)集R上的非負光滑函數(shù),p>0,加權(quán)無窮序列空間

lp(φ)={ξ=(ξ1,ξ2…):ξi∈R,

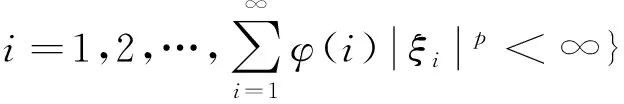
是一類重要的Banach空間,其中φ稱為權(quán)數(shù).lp(φ)中的范數(shù)由

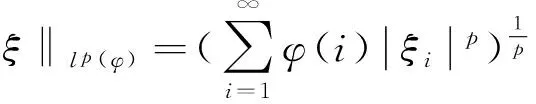
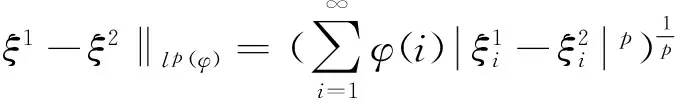
lp(φ)是lp的推廣,當φ=1時,lp(φ)為通常的序列空間lp.

我們首先給出與集合緊性相關(guān)的概念和結(jié)果[1-3].

定義1設(shè)X為度量空間,M是X的子集,M0是M的子集,ε>0.如果對任意的x∈M,總存在y∈M0,使得x屬于y的一個ε-鄰域U(y,ε),即x∈U(y,ε),那么稱M0是M的一個ε-網(wǎng).如果M0還是一個有限集合,則稱M0是M的一個有限ε-網(wǎng).

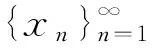
引理1設(shè)X為完備度量空間,M?X,則M是X中的列緊集的充要條件是對任意的ε>0,M在X中存在有限ε-網(wǎng).

例如，X=R1=(-∞,∞)是非緊區(qū)間,事實上,屬于它的數(shù)列ξn=2n,n=1,2，…不包含任何收斂子列.但由Bolzano-Weierstrass定理知R1中的任意有界集是列緊的,而任意有界閉集是自列緊的,即是緊的.因此,任意有限閉區(qū)間[a,b]是R1中的緊集,有限開區(qū)間(a,b)是列緊集.一般地,RN中的緊集與有界閉集是一致的.在一般度量空間X中,可以證明緊集一定是有界閉集,但反之不然,除非X是有限維空間. 例如,考慮加權(quán)空間lp(φ)中的單位球

Bφ={x:‖x‖lp(φ)≤1}.

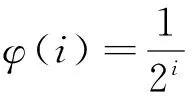
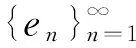
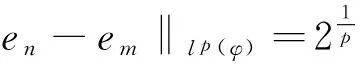
所以Bφ不是緊的.

下面給出加權(quán)無窮序列空間lp(φ)上的集合緊性判斷條件.這里的權(quán)數(shù)φ為定義在R上的非負光滑函數(shù).

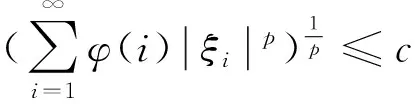
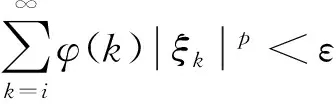
定理1設(shè)2≤p<∞,M為lp(φ)的子集,則M為列緊集的充要條件是：

(a)M在lp(φ)中一致有界;

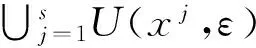
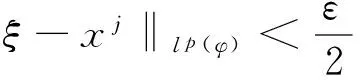
(1)

令c0=max{‖x1‖lp(φ),‖x2‖lp(φ),…,‖xs‖lp(φ)}.利用范數(shù)的三角不等式得到

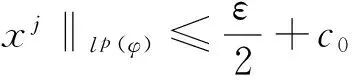
另一方面,利用ε-網(wǎng)中的這有限個元素{x1,x2,…,xs}?lp(φ),根據(jù)收斂級數(shù)的柯西準則,顯然可以找到共同的i0=i(ε)>0,使得當i≥i0時,

(2)

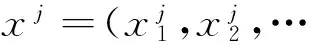
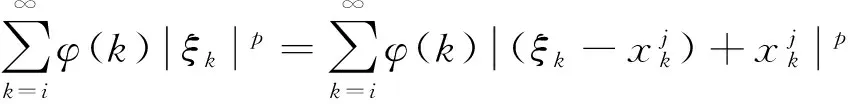
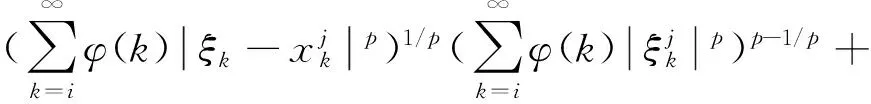
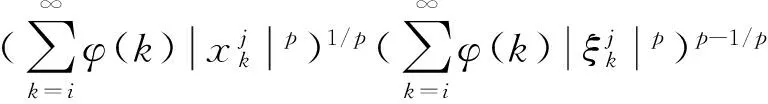
由此推出：

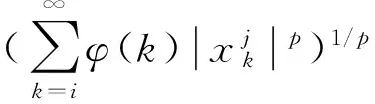
(3)

因此,根據(jù)(1)-(3)式,對(2)式中獲得的i0=i(ε)>0,當i≥i0時,對任意的ξ=(ξ1,ξ2，…)∈M,有：

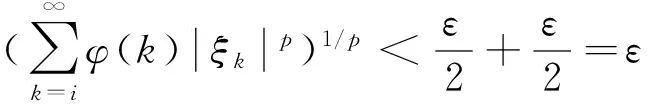
這表明對充分小的ε,有：

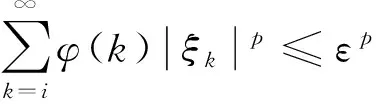
于是條件(b)得證.

充分性. 對任意的ε>0,根據(jù)條件(b),存在i0=i(ε)>0,當i≥i0時,對任意的ξ=(ξ1,ξ2，…)∈M,有：

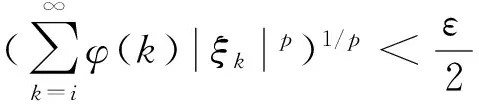
(4)

令

G0=max{φ(1),φ(2),…,φ(i0)}.

由于φ是非負連續(xù)函數(shù),故G0為有限正常數(shù).設(shè)集合

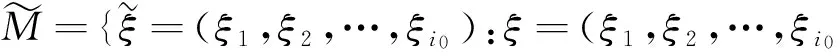
ξi0+1,…)∈M}

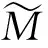
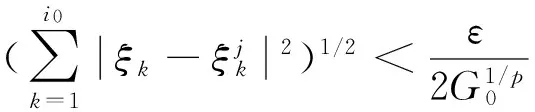
(5)

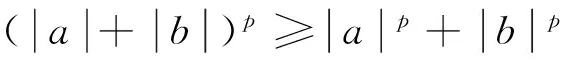
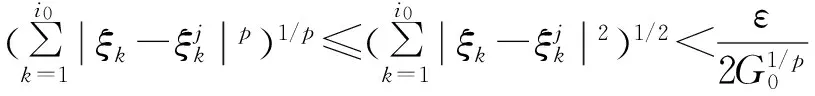
(6)

于是,根據(jù)(6)式有：

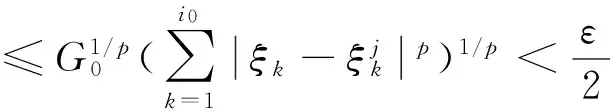
(7)

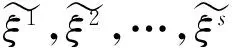
(8)

則容易驗證這樣得到的有限個無窮序列ξ1,ξ2,…,ξs屬于lp(φ).根據(jù)(4)式和(7)式,對任意的ξ=(ξ1,ξ2…)∈M,有

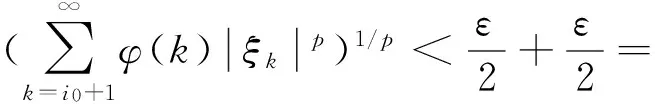
按(8)式定義的元素構(gòu)成的集合{ξ1,ξ2,…,ξs}為M在lp(φ)中有限ε-網(wǎng).由ε的任意性,再一次運用引理1,充分性得證.

[1]程其襄,張奠宙.實變函數(shù)與泛函分析基礎(chǔ)[M].北京：高等教育出版社,2003.

[2]郭懋正.實變函數(shù)與泛函分析[M]. 北京：北京大學出版社,2005.

[3]李國禎.實分析與泛函分析引論[M]. 北京：科學出版社,2004.

[4]邱曙熙,李毅軒.實變與泛函學習指導[M]. 廈門：廈門大學出版社,2004.

[5]李嘉,李揚榮.關(guān)于序列空間上的有界線性算子的教學探討[J].西南師范大學學報(自然科學版), 2012, 37(6): 225-229.

[6]林貴華.序列空間中的逼近性質(zhì)[J].大連理工大學學報(自然科學版),1996, 36(1):1-5.

(責任編輯穆剛)

Pre-compactness of sets in weighted space of infinite sequences

ZHAO Wenqiang1,ZHANG Yijin2

(1. School of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067,China；2. School of Science, Chongqing University of Posts and Telecommunications，Chongqing 400065, China)

The weighted infinite sequences space lp(φ)is a generalization of the general infinite sequences space lp.In this article, the compactness of sets M?lp(φ) is discussed for p≥2, and prove that M is pre-compact in lp(φ) if and only if M is uniformly bounded and uniformly convergent in some sense. The result obtained here enriches the contents of functional analysis.

weighted space of infinite sequences;compact set;ε-net;uniform boundedness; uniform convergence

2016-04-23

重慶市自然科學基金項目(cstc2014jcyjA00035);重慶市教育委員會科學技術(shù)項目(KJ1400430).

趙文強(1969—)，男，四川南江人，副教授，博士，主要從事泛函分析及其應用方面的研究.

O177. 3

A

1673-8004(2016)05-0012-03