基于CFD的離心泵結構參數優化

馬飛紅，唐鈴鳳，徐彬雪，萬　鵬

(安徽工程大學機械學院， 安徽　蕪湖　241000)

?

基于CFD的離心泵結構參數優化

馬飛紅，唐鈴鳳，徐彬雪，萬鵬

(安徽工程大學機械學院， 安徽蕪湖241000)

為獲得離心泵的最佳結構參數，根據給定的離心泵設計參數確定離心泵的結構形式和性能評價指標，計算離心泵各結構參數，利用CFD對離心泵進行流場數值模擬分析，設計了葉輪結構L16(45)正交實驗表，選擇葉輪進口安裝角βb1、出口安裝角βb2、包角φ、進口直徑D1、出口直徑D2為正交實驗的5個因素，完成了正交實驗并對實驗結果進行極差分析，得到各結構參數對各優化方向評價指標影響排序及其影響情況，構造出效率最大、汽蝕余量最小條件下的目標函數及統一目標函數，并運用遺傳算法對離心泵效率和汽蝕進行多目標優化，得到離心泵的最佳結構組合參數.

離心泵；CFD；正交實驗；極差分析；遺傳算法；最佳組合參數

離心泵是應用廣泛的一種水泵，它的開發過程中各項因素相互制約，造成開發過程漫長且復雜.在工程實際中，離心泵葉輪的設計依舊采用半理論半經驗的設計方法，設計出的模型性能通常不是最優的.因此，在傳統設計的基礎上對葉輪進行優化設計非常必要.

隨著計算流體力學的發展，CFD技術越來越受到設計人員的青睞.趙斌等人在基于CFD技術的離心泵葉輪優化設計時，為了減少重新設計的成本，在不改變泵整體結構的前提下，以葉輪型線為設計變量來優化葉輪尺寸[1].談明高等人針對離心泵出口角對能量性能的影響進行CFD研究，結果表明隨著葉片出口角的改變，泵的效率存在極值點[2].段敏等人基于CFD的離心泵三維內流場分析運用CFD軟件，采用標準湍流模型和SIMPLE算法對離心泵內流場進行分析，得到葉輪工作面和背面壓力分布的不均勻性[3].上述研究僅針對個別關鍵因素進行分析研究，未針對離心泵的多個結構因素進行流場分析及結構優化研究，且未使用優化算法對泵的各參數進行優化.本文采用CFD軟件對離心泵內流場進行模擬，并選取葉輪進口安裝角βb1、出口安裝角βb2、包角φ、進口直徑D1、葉輪出口直徑D2為正交實驗的5個因素，完成了正交實驗并對實驗結果進行極差分析，得到各結構參數對各優化方向評價指標影響排序及最佳組合參數及其影響情況，構造出效率最大和汽蝕余量最小條件下的目標函數及統一目標函數，并以D1、D2、b1、b2、βb1、βb2、Z為設計變量加以約束條件對離心泵進行全性能優化，運用遺傳算法對離心泵效率和汽蝕進行多目標優化，得到離心泵的最佳結構組合參數.

1　離心泵結構設計

離心泵的基本參數為：設計流量Q=25 m3/h，設計揚程H=80 m，額定轉速n=2 900 rpm，葉輪進口直徑D1=75 mm，D2=255 mm，葉輪進口寬度b1=20 mm，出口寬度b2=7 mm，進口安裝角βb1=25°，出口安裝角βb2=30°，包角φ=110°.根據上述參數，建立葉輪、蝸殼流道物理模型并裝配，如圖1所示.

圖1　流體域模型

2　CFD流場模擬

2.1網格劃分

網格劃分是流動控制方程數值離散的基礎，網格質量的好壞直接影響到解析的斂散性和結果的準確性.葉輪區網格數127 794，蝸殼區727 398，進口段網格數2 408，網格總數 854 692，如圖2所示.

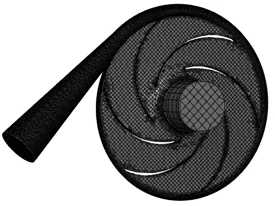
圖2　網格劃分

2.2控制方程

離心泵內部流動屬于三維、黏性、非定常湍流流動，其運動規律符合 Naiver -Stokes 方程.

連續方程：

(1)

動量方程：

(2)

不可壓N-S方程：

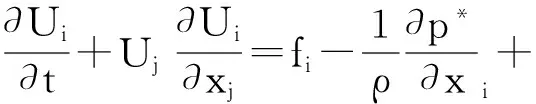
(3)

k-ε方程：

(4)

(5)

(6)

上式中，ρ是流體密度，p*是包括離心力的壓強，湍動能為k，ω是角速度，εijk是張量，μ是有效黏度系數，U為速度矢量，p是壓力，t是時間，?為流體運動黏性系數. i、j分別取1、2、3，σk=1.0，σε=1.3，Cμ=0.09，C1=1.44，C2=1.92.

2.3邊界條件設定

對邊界條件設置有: 流體介質的基本屬性，包括流體介質的密度、溫度、黏度大小、介質的含氣量、蒸汽密度、飽和蒸汽壓等，參數如表1所示.除此之外還要對葉輪葉片進行轉子設置，對流體介質的入口、出口進行設置以及旋轉面設置.

將壓力設為進口條件，將入口段進口處設為標準大氣壓.采用流量出口邊界條件，設置出口流量為額定工況流量，即Q=0.006 944 m3/s.將葉片設定為旋轉部件，轉速為2 900 rpm.將所有同葉輪一起旋轉的壁面(即葉輪的工作面和背面)均設置為旋轉壁面，轉速大小與葉輪葉片一致，且移動方向和速度要與葉輪保持一致.其余面可直接默認成靜止面.

2.4流場模擬

完成邊界條件設置后，設定計算迭代步數便進行求解計算，得到設計工況下離心泵葉輪內部流場的殘差動態監測過程.本文設定的計算迭代步數為1 000步.圖3為殘差曲線圖.從圖3中可以看出，迭代步數在達到500次左右時曲線已收斂.

圖3　殘差曲線圖

圖4為離心泵壓力分布圖.從圖4中可以看出，從葉輪進口處到葉輪出口處壓力數值是逐漸增加的，且靠近蝸殼出水口的壓力明顯大于葉輪中的其他區域，說明在葉輪旋轉過程中相對于蝸殼的不同位置，從葉輪到蝸殼液體流動不均勻，且蝸殼反作用于葉輪，使得葉輪中兩葉片之間可能出現渦流.

圖4　壓力云圖

圖5為離心泵速度分布圖.從圖5中可以看出，從葉輪進口處到葉輪出口處，速度的數值是逐漸增加的.由于葉片的作用使得靠近葉片處的流動效果比遠離葉片中心的流動效果要好，且相對遠離葉片的中間位置出現漩渦，嚴重影響葉輪區域液體的正常流動.

圖5　速度云圖

由圖6可以看出，離心泵葉輪范圍內出現明顯低壓區，且在靠近蝸殼的葉輪邊緣的葉片背面出現負壓區.

圖6　總壓分布圖

由圖7中可以看出，由于葉輪進口處壓力很低，達到介質在常溫下汽化的臨界壓力，故而葉輪進口處發生汽蝕，氣體體積分數高達0.848 36.這與實際情況相符.

圖7　氣體體積分數圖

3　正交實驗與極差分析

3.1正交實驗

離心泵的結構往往需要考察的實驗因素較多，進行全面實驗，模擬實驗規模大，實驗較為麻煩，且有可能因為實驗條件和實驗周期的限制而難以實施.

正交實驗是在試驗因素的全部水平值中尋找出部分有代表水平的組合進行實驗.通過較少次數實驗及對這些實驗結果的分析，得到全面的實驗情況，尋找到最優因素水平組合.綜合考慮離心泵的效率和汽蝕，選取葉輪進口直徑、出口直徑、葉輪進口角、出口角和包角5個結構尺寸作為實驗因素.每個因素設置4種水平，取值如表2所示.

在離心泵結構正交實驗中，不考慮各實驗因素間的交互作用，對于五因素四水平的正交實驗可以選用的正交表為L16(45).離心泵正交實驗的因素水平表如表2所示.

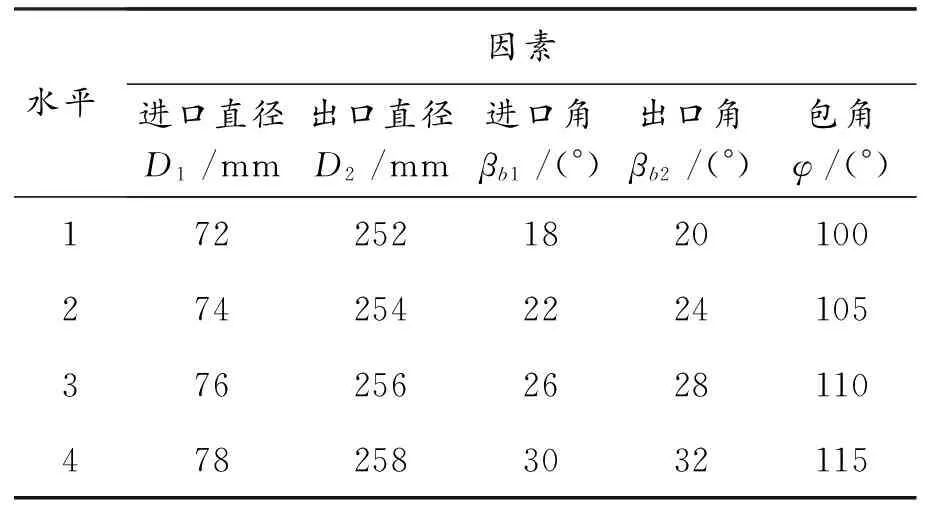
表2　葉輪正交實驗因素水平表

3.2極差分析

3.2.1各因素對效率的影響趨勢分析

根據表3計算各因素各水平下效率平均值的極差.從表4中可以明顯地看出各因素對效率的影響由大到小依次為：葉輪出口直徑D2、包角φ、進口直徑D1、進口角βb1、出口角βb2.為了更直觀地觀察變化趨勢，繪制了各因素對效率的影響趨勢圖如圖8所示.根據評價指標，得到最優水平組合為：A2B4C4D1E2，即當葉輪進口直徑D1為74 mm、出口直徑D2為258 mm、進口角βb1為30°、出口角βb2為20°、包角φ為105°時損失最小，表明此參數下的離心泵具有最大效率.該優化得到的離心泵結構參數不在已有的實驗中，用CFD軟件進行實驗驗證，得到該組數據的最大效率為56.80﹪，與已有的16組實驗數據對比發現該實驗效率接近正交實驗中的最大值.

考慮效率條件下的最佳組合參數：A2B4C4D1E2.最優水平組合為：A2B4C4D1E2，即當葉輪進口直徑D1為74 mm、葉輪出口直徑D2為258 mm、進口角βb1為30°、出口角βb2為20°、包角φ為105°時，可獲得最大效率，表明此參數下的離心泵具有最大效率.

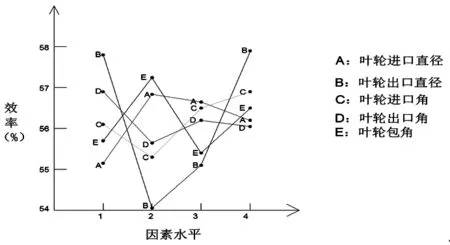
圖8　各參數對效率的影響趨勢

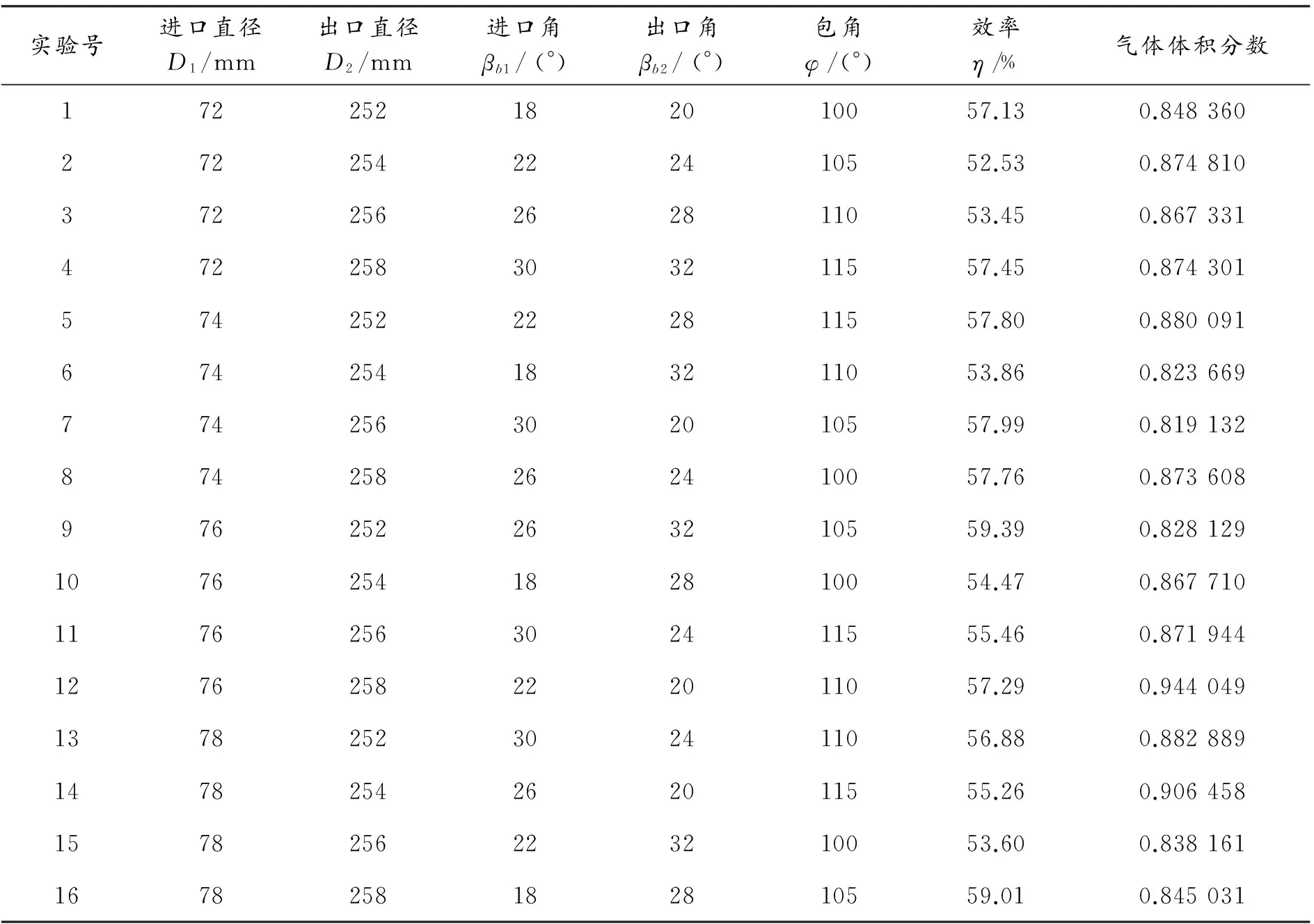
實驗號進口直徑D1/mm出口直徑D2/mm進口角βb1/(°)出口角βb2/(°)包角φ/(°)效率η/﹪氣體體積分數172252182010057.130.848360272254222410552.530.874810372256262811053.450.867331472258303211557.450.874301574252222811557.800.880091674254183211053.860.823669774256302010557.990.819132874258262410057.760.873608976252263210559.390.8281291076254182810054.470.8677101176256302411555.460.8719441276258222011057.290.9440491378252302411056.880.8828891478254262011555.260.9064581578256223210053.600.8381611678258182810559.010.845031

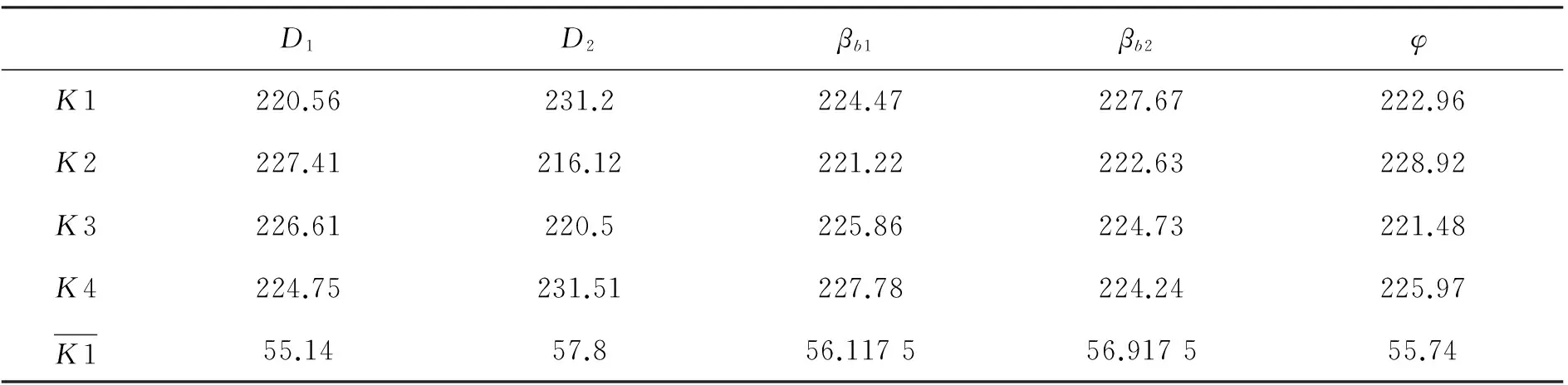
表4　各因素對效率的影響

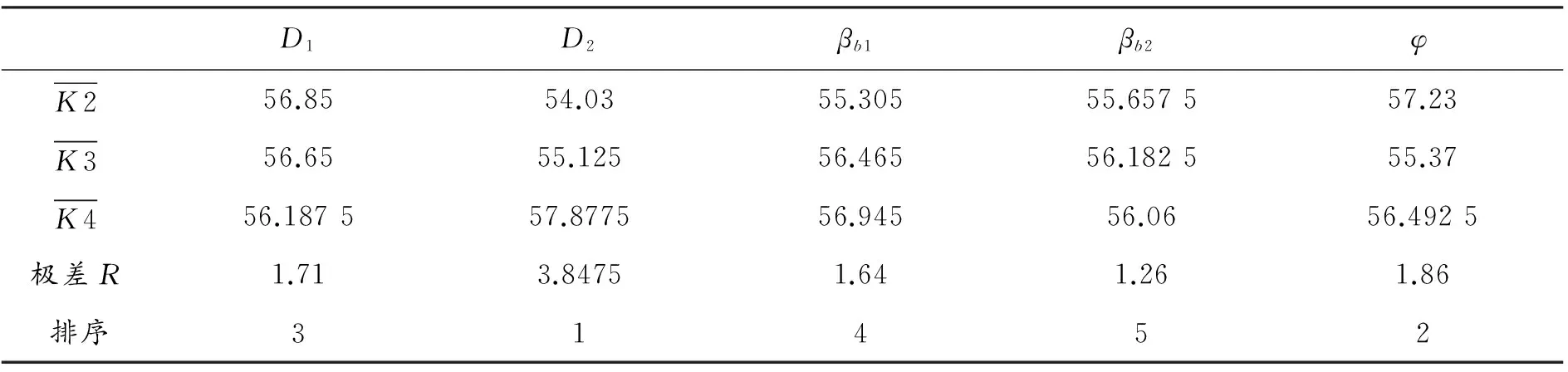
續表4

3.2.2各因素對汽蝕的影響趨勢分析

根據表3計算各因素各水平下氣體體積分數平均值的極差.從表5中可以明顯地看出各因素對汽蝕的影響由大到小依次為：進口角βb1、包角φ、葉輪出口直徑D2、出口角βb2、進口直徑D1.為了更直觀地觀察變化趨勢，繪制了各因素對氣體體積分數的影響趨勢圖如圖9所示.根據評價指標，得到最優水平組合為A2B2C1D3E1，即當葉輪進口直徑D1為74 mm、葉輪出口直徑D2為254 mm、進口角βb1為18°、出口角βb2為28°、包角φ為100°時，可獲得最小氣體體積分數，表明此參數下的離心泵的汽蝕有較好的改善.該優化得到的離心泵結構參數不在已有的實驗中.用CFD軟件進行實驗驗證，得到該組數據的最小氣體體積分數為0.843 46，與已有的16組實驗數據對比發現該實驗氣體體積分數接近正交實驗中的最小值.

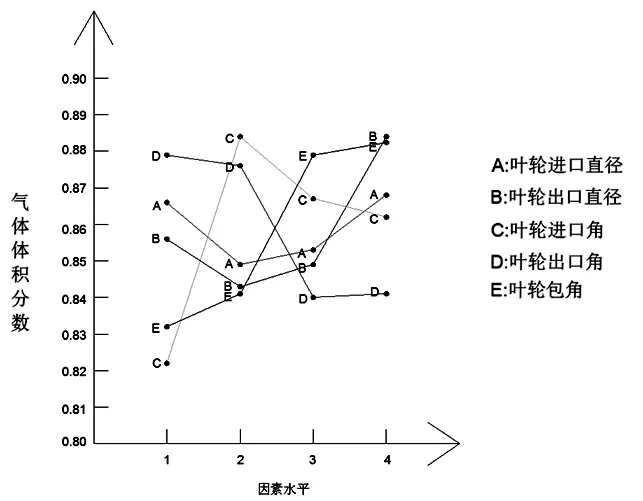
圖9　各參數對氣體體積分數的影響趨勢

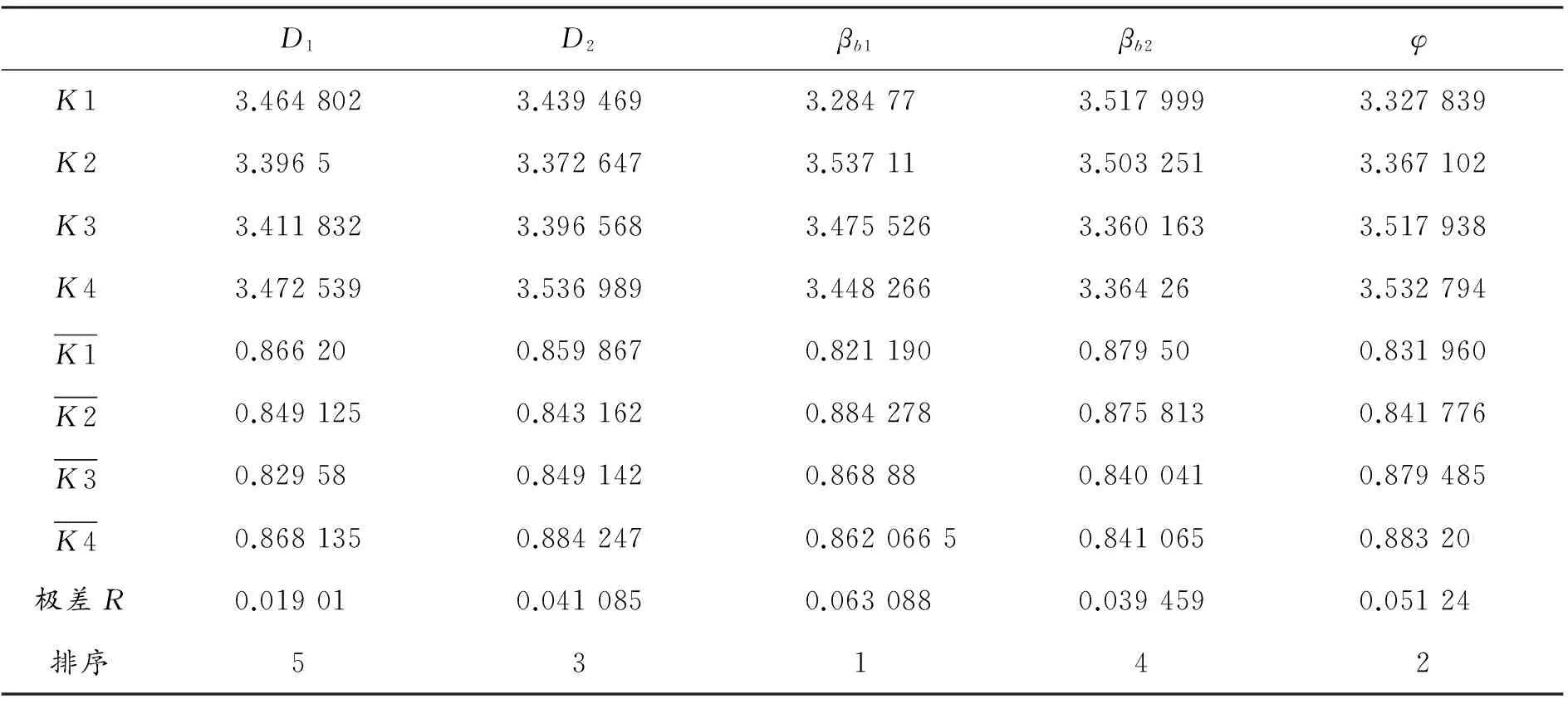
D1D2βb1βb2φK13.4648023.4394693.284773.5179993.327839K23.39653.3726473.537113.5032513.367102K33.4118323.3965683.4755263.3601633.517938K43.4725393.5369893.4482663.364263.532794K10.866200.8598670.8211900.879500.831960K20.8491250.8431620.8842780.8758130.841776K30.829580.8491420.868880.8400410.879485K40.8681350.8842470.86206650.8410650.88320極差R0.019010.0410850.0630880.0394590.05124排序53142

考慮汽蝕條件下的最佳組合參數A2B2C1D3E1.最優水平組合為A2B2C1D3E1，即當葉輪進口直徑D1為74 mm、葉輪出口直徑D2為254 mm、進口角βb1為18°、出口角βb2為28°、包角φ為100°時，可獲得最小氣體體積分數，表明此參數下的離心泵的汽蝕有了較好的改善.

4　遺傳算法優化

4.1離心泵效率最大目標函數

根據Stodola公式,當入口無預旋時，泵的理論揚程為：

(7)

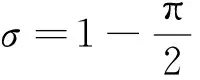
η=ηmηυηh

(8)

機械效率可表示為：

(9)

上式中的Pm是離心泵的機械損失，P是軸功率，且

容積效率可表示為：

(10)

(10)式中，ns為比轉數.可以看出，ηυ僅與n、Q和H有關，而這幾個參數都是不變量，因此可以推出ηυ是常量(用A表示).因此，總效率可表示為：

η=Aηmηh

(11)

水力效率可表示為:

(12)

其中，S為離心泵的水力損失.

將(9)、(12)式代入(11)式中可以得到離心泵總效率的表達式為：

(13)

由(13)式可以得出效率最大目標函數為:

(14)

4.2離心泵最小汽蝕余量目標函數

離心泵汽蝕余量基本方程為:

(15)

假定進口無預旋，則：

(16)

上式中，k1=0.876，k2=0.91，均為常數.

將(16)式代入(15)式可以得到：

(17)

汽蝕余量最小目標函數為：

min[f2(x)=NSPHr]

(18)

4.3目標函數處理

4.3.1統一目標函數

本文采用權重系數變換法處理多目標函數.對一個多目標優化函數，假設每個子目標函數fi(x)(i=1,2,…,n)賦予權重ωi，則各目標函數加權可表示為：

(19)

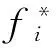
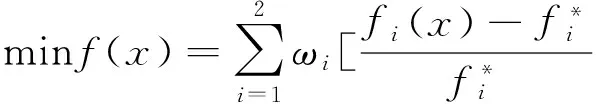
4.3.2分目標權重系數的確定

構造互補矩陣B(k)(k=1,2,…,n)的第一列列向量B1(k)=(b11(k),b21(k),…,bn1(k)).其中，n為矩陣的階數，b11(k)按(20)式計算：

b11(k)=(bk1)-1bk1,

b21(k) =(bk2)-1bk2,

……

bn1(k) =(bkn)-1bkn

(20)

構造超傳遞近似矩陣的第1列列向量

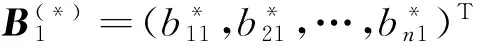
其中

(21)

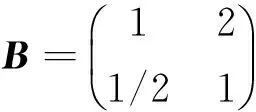
構造互補矩陣B(k)(k=1,2)第1列列向量為：

通過歸一化處理后，可得權重系數為：ω=(0.667,0.333).即ω1=0.667，ω2=0.333.

4.3.3約束條件

根據離心泵的水力模型對設計變量的取值范圍進行適當調整，可以得到其約束條件為：

(22)

4.4遺傳算法優化

本文采用遺傳算法工具箱GA進行目標優化，設置種群數為1 000，交叉概率0.7，變異概率0.01，以目標值相對誤差為收斂準則.相對誤差可表示為：

(23)

在MATLAB中進行GA程序，得到如圖10所示的迭代圖.優化結果如表6所示.

運用優化后的各參數重新建模，且對所建模型進行CFD分析.通過對優化的模型進行CFD

分析，可以通過泵的進出口壓差(如圖11所示)計算離心泵的效率為59.815 4﹪，與之前的56.80﹪相比提高了3.015 4﹪.從圖12中可以看出，優化后的模型在進行CFD分析后氣體體積分數為0.802 245，與之前的0.843 46相比減小了0.041 215，離心泵的整體性能有所提高.

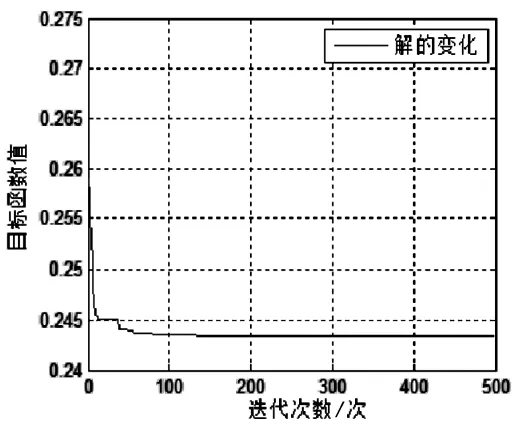
圖10　迭代收斂圖

圖11　優化后的壓力云圖

圖12　優化后的氣體體積分數

D1b1D2b2β1β2Z優化前7520255725306優化后78242506.820266

5　結論

(1)本文設計了L16(45)正交實驗表.各因素對離心泵效率的影響從大到小順序依次是：葉輪出口直徑D2、包角φ、進口直徑D1、進口角βb1、出口角βb2.效率條件下的最佳組合參數為：A2B4C4D1E2.各因素對離心泵汽蝕的影響從大到小順序依次是：進口角βb1、包角φ、葉輪出口直徑D2、出口角βb2、進口直徑D1.汽蝕條件下的最佳組合參數為：A2B2C1D3E1.

(2)運用遺傳算法對以效率最大和汽蝕余量最小為優化目標進行多目標優化，優化得到離心泵的最佳組合參數為：D1=78mm、D2=250mm、b1=24mm、b2=6.8mm、βb1=20°、βb2=26°、Z=6.

(3)通過對優化后的模型進行CFD分析，可以發現效率由之前的56.80﹪增加到59.815 4﹪，提高了3.0154﹪；氣體體積分數由之前的0.843 46減小到0.802 245，降低了0.041 215.可以看出，離心泵的整體性能有所提高.

[1]趙斌，孫鐵，周長茂，等. 基于CFD技術的離心泵葉輪的優化設計[J].石油化工設備技術，2007, 28(6): 43-45.

[2]談明高，劉厚林，袁壽其，等. 離心泵出口角對能量性能影響的CFD研究[J].中國農村水利水電，2008，(11):104-106.

[3]段敏，于海洋，葛鑫. 基于CFD的離心泵三維內流場分析[J].遼寧工業大學學報，2015，35(6): 392-395.

[4]李凱，唐鈴鳳，辛厚智. 脫硫除塵用風機流場模擬及其結構優化研究[J].重慶文理學院學報，2016(2)：109-115.

[5]馮喆. 離心泵葉輪內部流場模擬及其結構改進設計[J].機械設計與制造，2015, 5(5): 16-20.

[6]范恒艮，王幼民，唐鈴鳳. 離心泵內部流場的三維數值模擬及流動分析[J].機械工程師，2007(1): 49-51.

[7]張人會，楊軍虎，李仁年.離心泵葉輪的參數化設計[J].排灌機械工程學報，2009, 27(5): 310-313.

[8]LIY,DONGWL,HEZH.Flowinstabilityofacentrifugalpumpdeterminedusingtheenergygradientmethod[J].JournalofThermalScience, 2015, 24(1): 44-48.

[9]BACHAROUDISEC,FILIOSAE,MENTZOSMD,etal.Parametricstudyofacentrifugalpumpimpellerbyvaryingtheoutletbladeangle[J].OpenMechanicalEngineeringJournal, 2008, 2(5): 75-83.

[10]李敏強，寇紀淞，林丹．遺傳算法的基本理論與應用[M]. 北京：科學出版社，2002．

(責任編輯穆剛)

Optimization of structure parameters of centrifugal pump based on CFD

MA Feihong,TANG Lingfeng,XU Binxue,WAN Peng

(College of Mechanical and Automotive Engineering, Anhui Polytechnic University,Wuhu Anhui 241000, China)

In order to obtain the optimum structure parameters of the centrifugal pump, based on the design parameters of a given centrifugal pump, the structural form and performance evaluating index of centrifugal pump were determined and the structural parameters of the centrifugal pump were calculated. Using CFD to make flow numerical simulation analysis on centrifugal pump, theL16(45) orthogonal test table of Impeller structure was designed, selecting of impeller inlet angle, outlet angle, wrap angle, inlet diameter, outlet diameter as the five factors of orthogonal experiment,and the orthogonal experiment was completed and the range analysis of the results was made, and the influence of structure parameters were obtainedon the ranking optimization direction of evaluation index and the influence. The object function and unified objective function with the maximum efficiency and minimum cavitation were constructed, using genetic algorithm to optimize the efficiency and cavitation of centrifugal pump, and the best structure parameters of the centrifugal pump were obtained.

centrifugal pump; CFD; orthogonal experiment; range analysis; genetic algorithm; optimal combination parameter

2016-03-12

馬飛紅(1990—)，女，回族，安徽阜陽人，碩士研究生，主要從事機械制造及其自動化方面的研究.

TH11

A

1673-8004(2016)05-0049-08