道路放樣中具有卵形曲線的緩和曲線計算方法研究
■劉國光
(廣州南方測繪儀器有限公司廣東廣州510665)
道路放樣中具有卵形曲線的緩和曲線計算方法研究
■劉國光
(廣州南方測繪儀器有限公司廣東廣州510665)
在道路放樣中,經常會遇到不完整緩和曲線-卵形曲線的測設,對于卵形曲線要素計算過程在相關教材講述較少,本文通過補充完整緩和曲線的方法,以規則緩和曲線數學模型為基礎,由特殊曲線到一般曲線進行數據推導,并結合實際卵形曲線實例進行模型的驗證工作。
緩各曲線 卵形曲線 曲線要素
1 前言
卵形曲線是指用一條回旋線連接兩個同向曲線的組合曲線。卵形曲線的大圓必須把小圓完全包含在內。若大圓半徑無限大,即直線,其即屬于基本型。卵形曲線的回旋線不是從起點開始的完整回旋線,而是只使用曲率從到這一段的不完整回旋線。
在高等級公路與市政道路的匝道路線設計中,經常會遇到這種類型的曲線。由于其復雜性,在測量教材中,主要針對緩和曲線的兩種基本型:∞→R及R→∞,對卵形曲線缺少相應的描述。本文試圖通過補充完整曲線的方法計算卵形曲線要素,最后用實例進行驗證,編寫工具軟件進行算法驗證。
2 卵形曲線要素及坐標要素的推導
在測量學材中,我們常見的兩種緩和曲線形式為直線-緩和曲線-圓曲線-緩和曲線-直線形式,緩和曲線無非就兩種基本型:半徑從無窮大到R(從直線到圓)和從R到無窮大(從圓到直線),中線坐標計算公式如下,其中數學坐標系計算公式為:
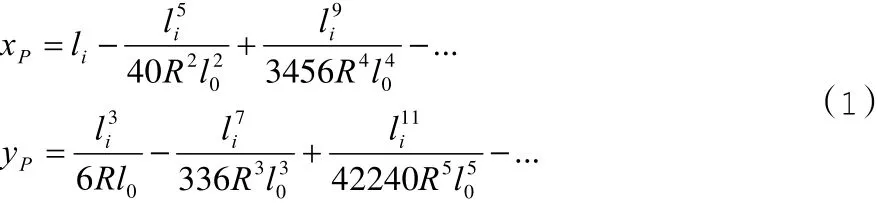
測量坐標系坐標轉換公式為:
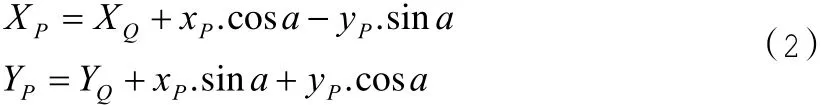
至此常規緩和曲線計算完畢。
在卵形曲線的計算中,經常會遇到圓曲線-緩和曲線-圓曲線的形式,即不完整緩和曲線,也是我們常說的卵形曲線,他是從一個半徑R1過渡到另外一個半徑R2,可分為從大半徑到小半徑,從小半徑到大半徑兩種形式,兩種形式均以向大半徑補充完整為原則,
第一種情況:當R1→R2(R1 向R2端補充完整緩和曲線,設補充段緩曲長為LX,由于 LR=A2,即緩和曲線長與半徑的乘積是一個常值,由此可知: 由此可得: 計算公式為:lI為任意點的緩曲長度,l0為完整級各曲線長度將lI和l0代入到(1)計算出XP、YP 坐標轉換公式為: 其中: 將xP、yP和α代入(2)可計算出P點的坐標。 第二種情況:當R1→R2(R1>R2)時: 向R1端補充完整緩和曲線,設補充段緩曲長為LX,由于LR=A2,即緩和曲線長與半徑的乘積是一個常值,由此可知: 由此可得: 計算公式為: 將lI和l0代入到(1)計算出xP、yP 坐標轉換公式: 將xP、yP和α代入(2)可計算出P點的坐標。 實 例 : 第 一 緩 和 曲 線 起 點 ZH:K137+864.087(2673320.152,497509.476)起始方位角143°48′13.1″ ,第一緩和曲線長224.01,第一圓曲線弧長1070.41半徑1800,第二緩和曲線長243.55,圓曲線弧長337.88半徑1100,第三緩和曲線長227.27 由數據分析可知: 第一段曲線為完整的標準緩和曲線∞→R,第二段為圓曲線,第三段即為本文研究的緩和曲線,屬于R1>R2類型,第四段也是圓曲線,第五段為也為標準的緩和曲線,為R→∞,本文主要研究第三段卵形曲線。 計算: 1、計算第一緩和曲線各點坐標,利用公式∞→R: 利用公式(1)計算各點在曲線坐標系中的坐標及利用坐標轉換計算出在測量坐標系中的坐標,起算方位角為143°48′13.1″ 2、計算第一圓曲線中各點的坐標,圓曲線有兩種計算方法,一種是利用綜合曲線中緩和曲線的計算方法,一種是直接用圓曲線計算,注意兩種曲線的起算方位與起算點具有差異性。 3、計算第二緩和曲線各點的坐標,利用R1→R2(R1>R2)中的公式 由于該緩和曲線是從大半徑到小半徑的變化,所以可利用公式(7)計算緩和曲線長,坐標轉換中坐標原點的計算利用公式(8),再利用坐標轉換計算公式計算,轉換角利用公式(9)計算,最終計算坐標轉換角175°20′59.56″ 坐標轉換中坐標原點的計算: 將代入下式中 利用公式計算出各樁號在曲線坐標系中的弧長,再利用公式(1)計算出各點在曲線坐標系中的坐標,然后利用公式(2)計算出該樁號在測量坐標系中的坐標。 4、計算第二圓曲線各點的坐標,方法同二。 5、計算第三緩和曲線各點的坐標,方法同一。 本文卵形曲線相關算法經過編寫工具軟件GPSTOOL驗證通過,軟件結果表明,用補全法計算卵形曲線中線坐標回歸完整曲線,然后利用一般的緩和曲線算法:從直線到圓和從圓到直徑的兩種緩和曲線形式進行計算,由特殊到一般,易于理解的同時,精度也能達到保證,易于編程實現,在實踐驗證中取得比較好的效果。 [1]張正輝,李海鵬,何方海.卵形曲線的坐標計算 [J].交通標準化,2007,3(2):129-130. [2]張家平,崔旭光,趙德龍.卵形曲線測設與計算要點解析 [J].黑龍江工程學報,2008,22(3):29-31. [3]鐘孝順,聶讓.測量學 [M].北京:人民交通出版社,2001. [4]呂會軍 龍曉榮.關于卵形曲線的平面坐標計算探討 [J].中國水運,2007,5(6): P2[文獻碼]B 1000-405X(2016)-5-304-2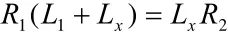
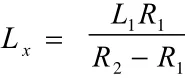



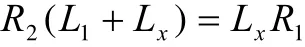
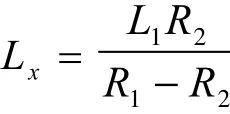
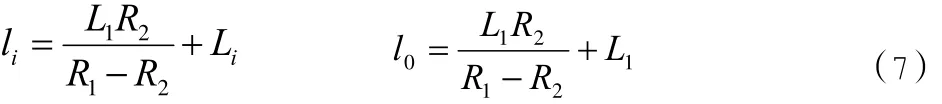
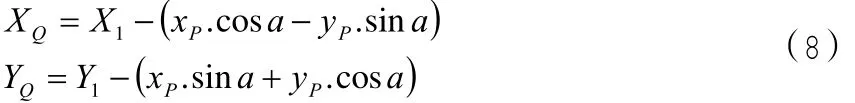

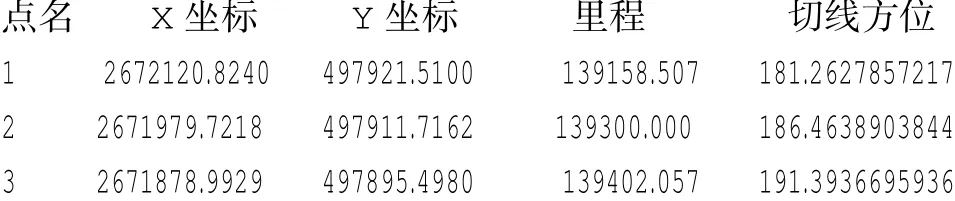
3 卵形曲線實例
4 結論

