具有廣義多面體約束的參數(shù)變分不等式解映射伴同導數(shù)

龐 麗 萍，　呂 佳 佳，　孟 凡 云，　王 金 鶴

( 1.大連理工大學 數(shù)學科學學院, 遼寧 大連　116024；2.青島理工大學 計算機工程學院, 山東 青島　266033 )

?

具有廣義多面體約束的參數(shù)變分不等式解映射伴同導數(shù)

龐 麗 萍*1，呂 佳 佳1，孟 凡 云1，王 金 鶴2

( 1.大連理工大學 數(shù)學科學學院, 遼寧 大連116024；2.青島理工大學 計算機工程學院, 山東 青島266033 )

在研究參數(shù)變分不等式穩(wěn)定性理論及均衡約束數(shù)學規(guī)劃的最優(yōu)性條件時，計算參數(shù)變分不等式解映射的伴同導數(shù)顯得尤為重要．考慮了具有等式約束的廣義多面體約束的參數(shù)不等式．首先，在無約束規(guī)范條件下，利用二階微分理論，給出了具有廣義多面體約束的法錐的圖的法錐．其次，借助輔助多面體集合及約束規(guī)范條件，得到了更為簡潔的法錐形式．最后，給出參數(shù)變分不等式的解映射的伴同導數(shù)．

參數(shù)變分不等式；廣義多面體；伴同導數(shù)

0　引　言

在Banach空間X，Y，Z及其對偶空間X*，Y*，Z*中，考慮下面的參數(shù)變分不等式：

v∈f(x，p)+N(x;Ω)；對所有的x∈Ω

x∈X為決策變量，v、p為擾動參量，其中v∈X*是標準擾動變量，p∈Z是基本擾動變量．函數(shù)f：X×Z→X*嚴格可微．上述變分不等式可以等價地表示為下面的標準變分不等式：對v∈X*，p∈Z，存在x∈X使得

〈f(x，p)-v，z-x〉≥0；對所有的z∈Ω

許多優(yōu)化問題，比如參數(shù)互補問題、均衡問題、KKT系統(tǒng)等都可以用上述參數(shù)變分不等式表示．在本文中考慮Ω是下面定義的廣義多面體：

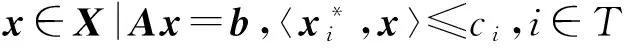
S(v，p)={x∈X|v∈f(x，p)+N(x;Ω)}

近年來許多學者對參數(shù)變分不等式進行了研究，而且取得了不少成果[1-3]．而參數(shù)變分不等式的解映射也是研究的一個極其重要的方面，它為具有均衡約束的優(yōu)化問題的最優(yōu)性條件[4]及穩(wěn)定性分析[1]提供了重要的理論依據(jù)．近年來，對這一問題研究取得了許多重要的進展．Henrion等在文獻[5]中利用二階微分理論得到了無限維Banach 空間中具有多面體約束的參數(shù)變分不等式解映射的伴同導數(shù)．此后，Ban等在文獻[6]中建立了廣義多面體約束的參數(shù)變分不等式的解映射的伴同導數(shù)．此外，以c為變量得到擾動集合Ω(c)，文獻[7-8]建立了此類多面體約束的參數(shù)變分不等式的微分理論．本文將文獻[5]中的多面體推廣到具有線性等式約束的廣義多面體，在半無限線性規(guī)劃及無限維空間的廣義線性規(guī)劃中，許多問題的約束都可以寫成上述形式的廣義多面體，因此研究廣義多面體集合具有十分重要的意義．對于帶有線性等式約束的廣義多面體，為了得到廣義多面體集合法錐映射的圖的極限法錐的簡潔形式，不能像文獻[5]中定理4.2那樣直接證明得到，因此借助定義的輔助多面體集合，首先建立輔助多面體集合的法錐映射的圖的極限法錐的簡潔形式，然后建立廣義多面體的法錐映射的圖的極限法錐的簡潔形式，最后建立具有廣義多面體約束的參數(shù)變分不等式解映射的伴同導數(shù)．

1　預備知識

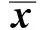
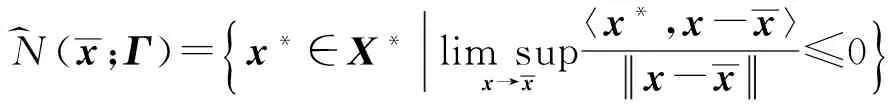
N^(x;Γ)={x*∈X*limsupx→xx-x≤0}

(1)

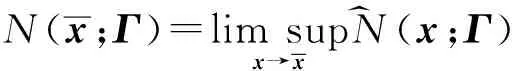
N(x;Γ)=limsupx→xN^(x;Γ)

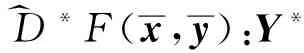
(2)

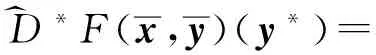
D^*F(x,y)(y*)=

{x*∈X*|(x*，-y*)∈

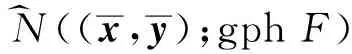
N^((x,y);gphF)

}

(3)

伴同導數(shù)(或極限伴同導數(shù)或Mordukhovich伴同導數(shù))定義為

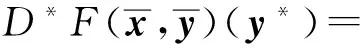
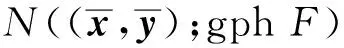
(4)

定理1 W為向量空間，A：W→Rd和B：W→Rs為線性映射．則下述兩系統(tǒng)之一有解：

(1)?x∈W使得Bx≥0，Ax>0；

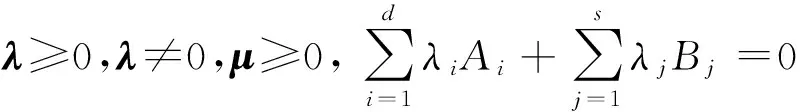
2　廣義多面體約束的法錐映射的伴同導數(shù)

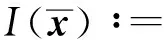
(5)

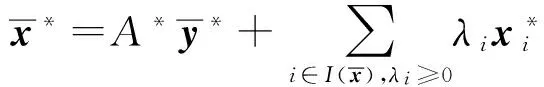
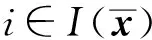
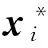
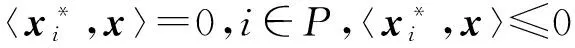
i∈QP}

其中

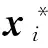
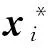
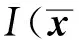
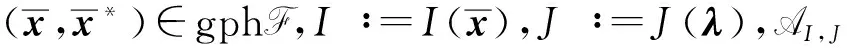
N^((x,x*);gphF)=

[AI，J+A*Y*]×

[BI，J∩ker A]

固定Q?T，令

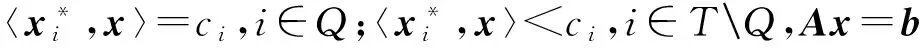
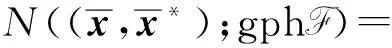
A*Y*]×[BQ，P∩ker A]

(6)

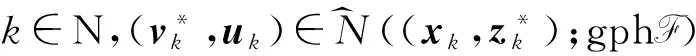
k∈N,(v*k,uk)∈N^((xk,z*k);gphF)

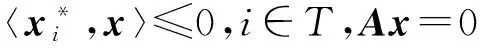
(7)

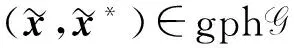
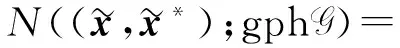
(8)

證明 將定理3應(yīng)用到輔助多面體集合得

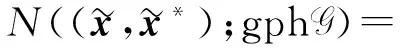
A*Y*]×

(9)

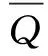
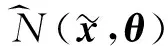
N^(x,θ)

(10)

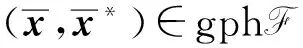
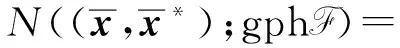
[BQ，P∩ker A]

(11)

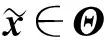
最后，給出具有廣義多面體約束的參數(shù)變分不等式的解映射的伴同導數(shù)．

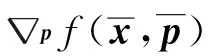
pf(x,p)

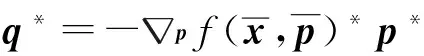
q*=-pf(x,p)*p*

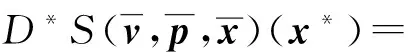
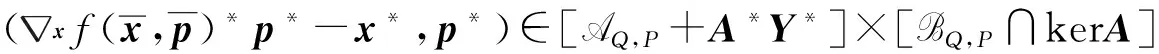
(xf(x,p)*p*-x*,p*)∈[AQ,P+A*Y*]×[BQ,P∩kerA]

}

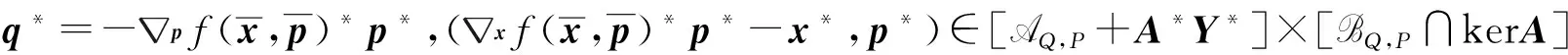
q*=-pf(x,p)*p*,(xf(x,p)*p*-x*,p*)∈[AQ,P+A*Y*]×[BQ,P∩kerA]

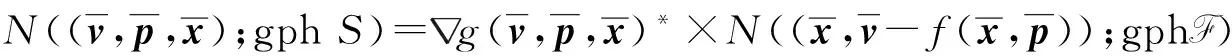
N((v,p,x);gphS)=g(v,p,x)*×N((x,v-f(x,p));gphF)

證明 (i)對(v，p，x)∈gphS，定義映射g：X*×Z×X→X×X*為g(v，p，x)∶=(x，v-f(x，p))，則gphS={(v，p，x)∈X*×Z×X|g(v，x，p)∈gph F}=g-1(gph F)．應(yīng)用文獻[9]中定理1.17，可得，由伴同導數(shù)的定義及定理3知存在P?Q?I，P∈I，SQ≠?，滿足

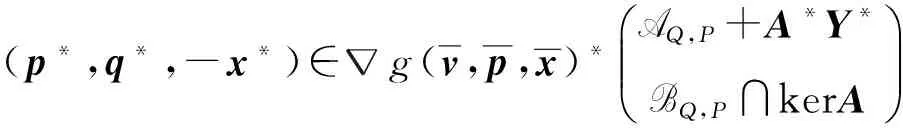
(p*,q*,-x*)∈g(v,p,x)*AQ,P+A*Y*BQ,P∩kerA?è????÷÷

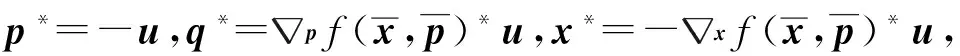
p*=-u,q*=pf(x,p)*u,x*=-xf(x,p)*u,

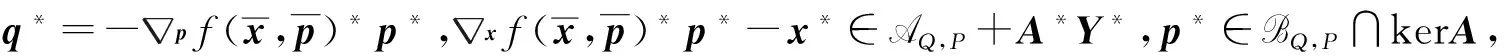
q*=-pf(x,p)*p*,xf(x,p)*p*-x*∈AQ,P+A*Y*,p*∈BQ,P∩kerA,

則存在u∈AQ，P+A*Y*，u*∈BQ，P∩ker A滿足即對P?Q?I，P∈I，SQ≠?，有則(i)的結(jié)論成立．

(ii)由定理5知，在兩個約束規(guī)范條件之下，有式(11)成立，則(ii)同樣成立．

3　結(jié)　論

本文主要建立了帶有廣義多面體約束的參數(shù)變分不等式的解映射的伴同導數(shù)．從不同的角度對文獻[6]進行了深入的推廣．首先，在無約束規(guī)范的條件下，得到了法錐映射的圖的法錐．其次，借助輔助多面體集合及約束規(guī)范，得到了更為一般的法錐形式．最后，得到參數(shù)變分不等式的解映射的伴同導數(shù)．

[1]Dontchev A L, Rockafellar R T. Characterizations of stronger regularity for variational inequalities over polyhedral convex sets [J]. SIAM Journal on Optimization, 1996, 6(4):1087-1105.

[2]LU Shu, Robinson S. Variational inequalities over perturbed polyhedral convex sets [J]. Mathematics of Operation Research, 2008, 33(3):689-711.

[3]Mordukhovich B S, Nghia T T A. Local strong maximal monotonicity and full stability for parametric variational systems [J]. SIAM Journal on Optimization, 2016, 26(2):1032-1059.

[4]Ye J J, Zhu Q J. Multiobjective optimization problems with variational inequality constraints [J]. Mathematical Programming, 2003, 96(1):139-160.

[5]Henrion R, Mordukhovich B S, Nam N M. Second-order analysis of polyhedral systems in finite and infinite dimensions with applications to robust stability of variational inequalities [J]. SIAM Journal on Optimization, 2010, 20(5):2199-2227.

[6]BAN Li-qun, Mordukhovich B S, SONG Wen. Lipschitzian stability of parametric variational inequalities over generalized polyhedra in Banach space [J]. Nonlinear Analysis: Theory, Methods & Application, 2011, 74(2):441-461.

[7]Nam N M. Coderivatives of normal cone mappings and Lipschitzian stability of parametric variational inequalities [J]. Nonlinear Analysis: Theory, Methods & Application, 2010, 73(7):2271-2282.

[8]Qui N T. Nonlinear perturbations of polyhedral normal cone mappings and affine variational inequalities [J]. Journal of Optimization Theory and Applications, 2012, 153(1):98-122.

[9]Mordukhovich B S. Variational Analysis and Generalized Differentiation I:Basic Theory [M]. Berlin:Springer, 2006.

Coderivative of solution mapping to parametric variational inequality constrained by generalized polyhedra

PANGLi-ping*1,LüJia-jia1,MENGFan-yun1,WANGJin-he2

( 1.School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China；2.Computer Engineering Institute, Qingdao Technological University, Qingdao 266033, China )

It is of great importance to compute the coderivative of the solution mapping to the parametric variational inequality while investigating the stability theory of the parametric variational inequality and optimality conditions of the mathematical programming governed by equilibrium constraints. A class of parametric variational inequalities constrained by generalized polyhedra including the equality constraints is considered. Firstly, by virtue of the second-order differentiation theory, the normal cone is given to graph of the normal cone constrained by generalized polyhedra without any constraint qualifications. Next, under the auxiliary polyhedral set and the provided constraint qualification, the formula of the above-obtained normal cone is simplified. Finally, the coderivative of the solution mapping to the parametric variational inequality is given.

parametric variational inequalities; generalized polyhedra; coderivative

1000-8608(2016)05-0546-05

2016-02-01；

2016-07-28．

國家自然科學基金資助項目(11171049,31271077,11301347).

龐麗萍*(1968-)，女，教授，博士生導師，E-mail:lppang@dlut.edu.cn；呂佳佳(1987-)，女，博士生，E-mail:ljiajia2849@163.com；孟凡云(1987-)，女，博士生，E-mail:mengfanyundlut@163.com.

O224

A

10.7511/dllgxb201605016