信道估計誤差對ZFBF總速率性能的影響分析
李 寧,張 超,翟立君,劉 允
信道估計誤差對ZFBF總速率性能的影響分析
李 寧1,張 超2,翟立君1,劉 允1
(1.中國電子科技集團公司第五十四研究所,河北石家莊050081;2.華中科技大學電子信息與通信學院,湖北武漢430074)
迫零波束成形是一種簡單易行的多用戶多輸入多輸出 (MIMO)下行鏈路線性預編碼算法,在用戶數充分大時,可以獲得接近多用戶MIMO下行總速率容量的性能,但是其波束的構造對信道狀態信息的精度也有很高的要求。對信道估計誤差導致的系統總速率損失進行了建模分析,并得到總速率的2種近似表達式,進而在此基礎上以最大化系統有效總速率為目標推導出最優的信道訓練時長公式。通過仿真實驗驗證了此模型的合理性與準確性,對于實際系統的性能分析及設計具有一定的指導意義。
MU-MIMO;ZFBF;信道估計;最優訓練序列長度
引用格式:李 寧,張 超,翟立君,等.信道估計誤差對ZFBF總速率性能的影響分析[J].無線電工程,2016,46(5):25-28,102.
0 引言
多用戶 MIMO技術(Multi-user MIMO,MUMIMO)可以獲得多址容量的增益[1]。其實現方法有:臟紙編碼(Dirty Paper Code,DPC)被證明能夠達到理論的信道容量[2],但實現復雜度極高;迫零波束成型(Zero-Forcing Beam Forming,ZFBF)[3-4]實現簡單,在用戶數充分大時,多用戶分集效應使ZFBF也可以獲得接近DPC的總速率性能,因此得到了廣泛的研究。
經典ZFBF算法假設基站可以獲得理想的信道的狀態信息(Channel State Information,CSI),而在實際的系統中,只能將信道信息量化后反饋給基站。由于頻譜資源有限,在信道相干時間內反饋信道僅僅可以提供有限的反饋比特數,因此會帶來速率損失。文獻[5-8]對有限反饋的量化誤差對總速率性能帶來的影響進行了分析,并提出了改進方案。但都沒有關注信道估計誤差對系統總速率性能的影響。
本文對多用戶MIMO下行鏈路的ZFBF算法進行了分析,將信道估計誤差考慮在內,分有用戶調度與無用戶調度2種場景分析信道估計誤差對ZFBF總速率性能的影響,并在此基礎上以最大化有效傳輸速率為目標,計算得到最優的訓練序列長度。
1 系統模型
考慮如圖1所示的單小區多用戶MIMO通信系統的下行鏈路,假設小區中有K個用戶,基站配有M根天線,每個用戶均配備單天線。用戶k的信道用1×M的行向量hk表示,則系統的信號模型為:

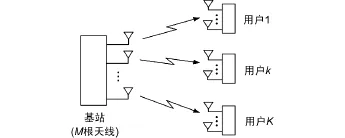
圖1 多用戶MIMO下行信道示意
對第k個用戶,記sk、wk和Pk分別為對應的發送符號向量、預編碼波束向量和發射功率縮放系數,則用戶k對應的發射信號為Pkwksk,接收信號為:
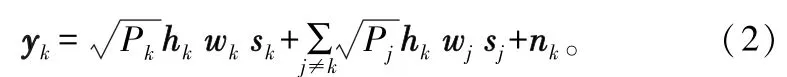
式中,第1項是期望信號;第2項為其他用戶信號造成的干擾;第3項為高斯噪聲。ZFBF算法的基本思想是通過預編碼向量的設計使期望接收端的干擾信號為0,即選擇wj,使hkwj=0,?j≠k。
2 信道估計誤差對總速率性能的影響
在多用戶MIMO系統中,下行波束的構造很大程度上依賴于信道的狀態信息,信道狀態信息的獲取需要由發送端發送訓練序列,并在接收端進行信道估計。假設訓練序列長度為T,用M×T維的矩陣S表示訓練序列矩陣,接收端采用最小均方誤差(Minimum Mean Square Error,MMSE)算法進行估計,由于在MIMO信道中采用酉陣作為訓練矩陣是MSE最優的[9],因此按照下面的標準選取S:
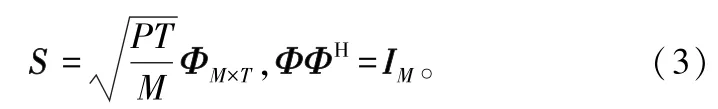
式中,P為基站的發射功率,對應的接收信號為:
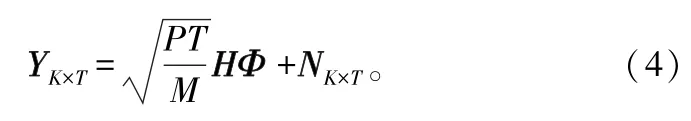
信道矩陣的MMSE估計為[9-10]:
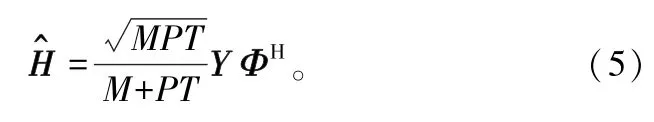
根據式(5),信道矩陣可以表示為估計矩陣與誤差矩陣的和:H=H^+E,估計矩陣H^和誤差矩陣E相互獨立并且它們的元素均為零均值、循環對稱的復高斯分布,方差分別為:
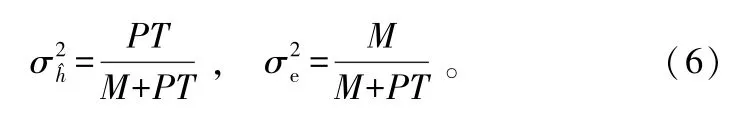
ZFBF實現的前提條件是同時傳輸的用戶數不大于發射天線數,即K≤M。當K>M時需要先進行用戶調度,即從所有用戶中選出M個用戶,然后在選出的用戶組內構造波束矢量。下面分2種情況進行分析。
①K≤M
當K≤M時,不需要進行用戶調度。基站根據信道估計值構造迫零單位波束矢量,即
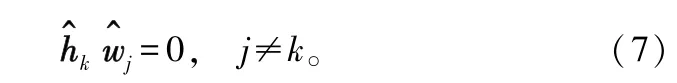
假設對所有用戶等功率分配,則每個用戶的接收信號為:
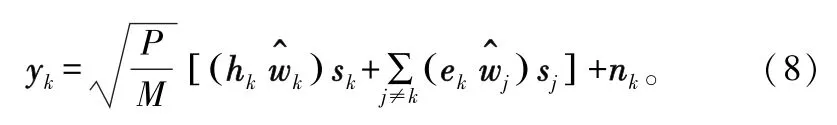
式(8)括號內的第2項表示多用戶干擾。式中,ek表示用戶k的信道估計誤差向量。接收機將干擾項視為加性高斯噪聲,則對應的遍歷總速率為:
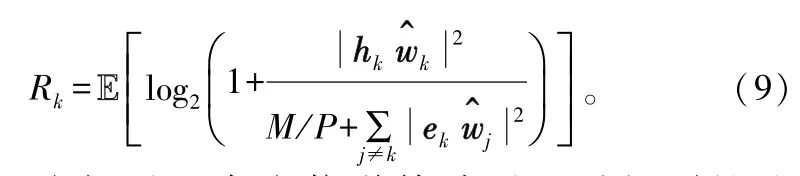
記wk為假設不存在信道估計誤差時得到的迫零波束向量,則對應的遍歷總速率為:
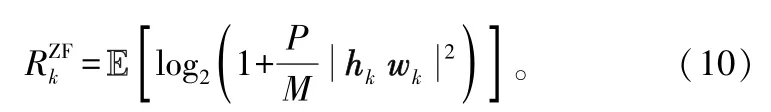
定義ΔRk?RZFk-Rk為理想情況下的總速率與存在信道估計誤差時的總速率差值,即信道估計誤差帶來是速率損失,可以得出這一差值的上界為[9]:
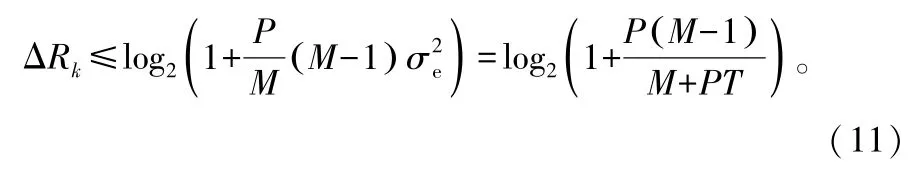
由這個上界可以得到M個用戶的總速率的近似值:
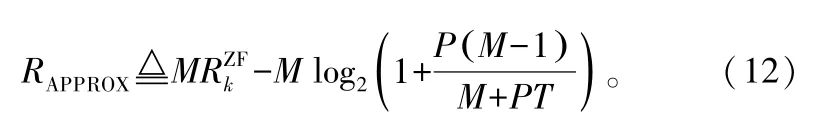
另外,從式(11)可以看出,隨著P的增長,速率損失逐漸增大,因此,在高信噪比條件下要維持系統的性能需要提高信道估計的精度。所幸的是,當P→∞時,ΔRk的上界將趨于一個常數,即
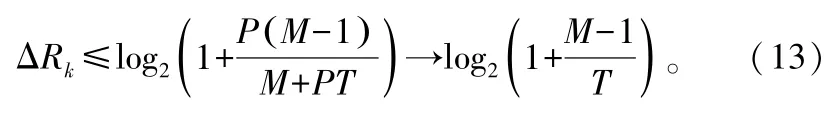
②K>M
當用戶數很大時,采用窮搜索實現用戶調度的復雜度過高,因此經常使用低復雜度的次優用戶選擇算法。半正交用戶選擇(Semiorthogonal User Selection,SUS)算法[3]是在所有用戶中選出一組半正交(空間分離度高)且信道質量好的用戶,可以證明基于SUS算法的ZFBF是漸進最優的,本文中使用這一算法進行用戶調度,再構造波束向量。由于SUS算法與信道估計過程相互獨立,所以SUS算法對ΔRk造成的影響相對較小,因此仍然可以用式(11)作為ΔRk的近似值。定義如下總速率的近似表達式:
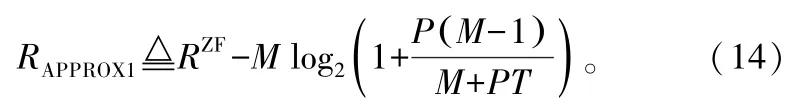
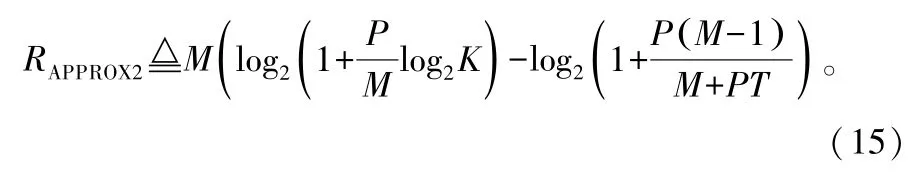
3 最優訓練長度
假設相干時間長度為Tc,用于信道估計的訓練時隙數為T,(T≥M),每個時隙長度為τ。則用于數據傳輸的時間為Tc-Tτ(忽略信息反饋、估計有效信道信息等操作)。假設實際的數據傳輸速率為R,令α=τ/Tc,可以定義有效傳輸速率為Reffec?(1-αT)R,定義最優訓練時隙數為使有效傳輸速率最大的T,即
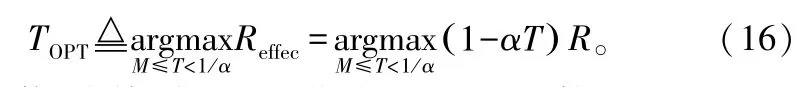
考慮信道估計誤差帶來的影響,使用RAPPROX2來近似R。因此,近似的最優訓練時隙數為:
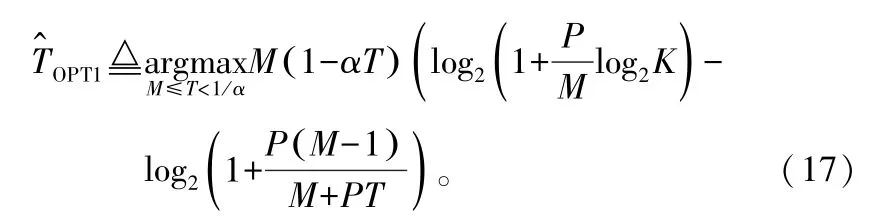
求(1-αT)RAPPROX2對T的導數并令其為0,可以求出T^OPT1的值。由于求導后的表達式難以直接求出閉合解,當 α取值較小且 P取值較大時,對式(17)中的求優表達式做進一步近似:
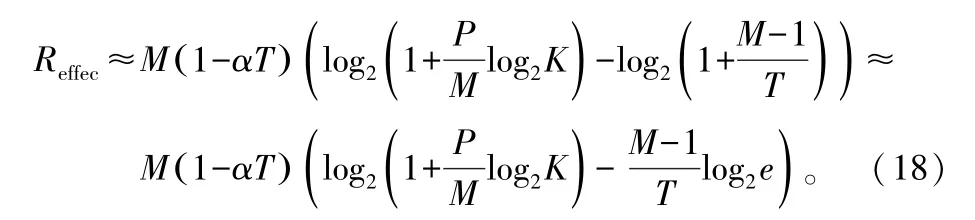
接下來對T求導并令其值為0,可得TOPT的另一個近似值:
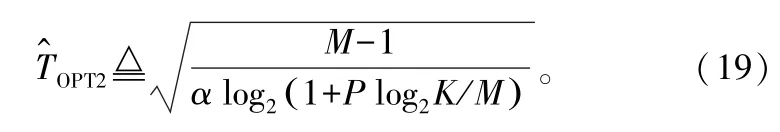
下面將通過仿真分析 T^OPT1和 T^OPT2的近似程度,以及TOPT隨P的變化規律。
4 仿真結果
為了驗證上述分析的準確性,將根據文中數學模型得到的分析結果與實際系統仿真進行比對。仿真建立在圖1所示的系統模型下,發射天線數目M=4,接收天線數目為1,信道為平坦瑞利衰落,其元素服從均值為0、方差為1的復高斯分布。
T=6、無用戶選擇時,總速率-平均SNR的仿真圖如圖2所示。圖2中“理想CSIT”是不考慮信道估計誤差的理想情況下系統總傳輸速率曲線,“實際速率”是采用 MMSE信道估計的實際仿真結果,“近似速率”則根據式(12)對傳輸速率的近似表達得出的仿真結果。可以看出近似速率與實際速率的變化趨勢基本相同,且差值并不大,尤其是在高SNR時,近似速率非常接近實際速率,充分說明了近似式(12)的準確性。
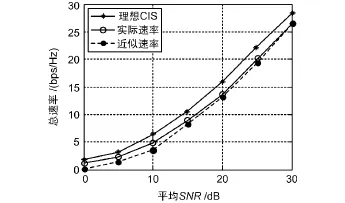
圖2 信道估計誤差對總速率性能的影響(K=4,T=6)
K=100,T=6時的總速率-平均SNR的仿真圖如圖3所示。圖3中“近似速率1”和“近似速率2”分別對應 RAPPROX1和 RAPPROX2。從圖 3中可以看出,高SNR時RAPPROX1與實際速率非常接近,說明采用SUS算法進行用戶調度對ΔRk的界定沒有什么影響。RAPPROX2的近似效果略差,這是由于使用M log2(1+P log2K/M)來近似RZF帶來的影響,但是差值并不大,在信噪比30 dB時,RAPPROX2與實際速率的差值大約為1 bps/Hz。因此,在一些定性分析的場景中完全可以使用 RAPPROX2來代替實際速率。
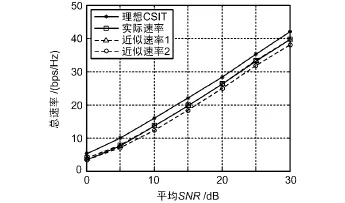
圖3 信道估計誤差對總速率性能的影響(K=100,T=6)
K=100,P=15 dB時,有效總速率-訓練時隙數的仿真圖如圖4所示。α取值分別為0.005、0.01 和0.02。圖4中的實線為實際的仿真值,虛線則是根據RAPPROX2得到的近似值。從圖4中可以看出,雖然近似值和實際值在數值上有比較明顯的差異,但是它們的變化趨勢很相似,極值點的位置也基本相同,因此根據 RAPPROX2得到的 T^OPT1能較好地刻畫TOPT。另外,注意到TOPT附近的幾個T值對應的有效速率與最大的有效速率值很接近,如果考慮到仿真中存在的誤差,取這幾個值作為最優值都是可以接受的,考慮實際系統設計時用于信道估計的開銷越小越好,在實際應用中訓練序列長度可以在TOPT附近選取較小的值。
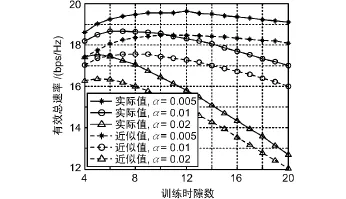
圖4 有效總速率-訓練時隙數仿真(K=100,P=15 dB)
K=100,α分別取0.001和0.005時,最優訓練時隙數-平均SNR的仿真圖如圖5和圖6所示。圖5和圖6中的實線為TOPT的實際仿真值,“近似1”和“近似2”分別代表PT1和OPT2。可以看出T^OPT1和T^OPT2的近似程度都較好。因此利用式(19)可以近似分析TOPT隨α、P、K和M等參數的變化規律。式(19)也顯示出,隨著信噪比的增加,需要的訓練序列長度減小,這與圖中的變化趨勢也是一致的。
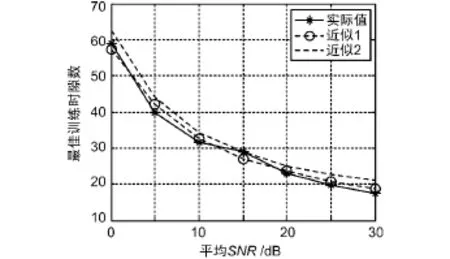
圖5 最優訓練時隙數仿真(K=100,α=0.001)
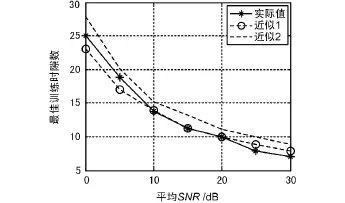
圖6 最優訓練時隙數仿真(K=100,α=0.005)
5 結束語
本文在MU-MIMO環境下,對存在信道估計誤差時的ZFBF傳輸過程建立模型,分析了信道估計誤差帶來的速率損失,并得出下行總速率的近似表達;進而以最大化有效總速率為目標,求得訓練序列的最優長度;最后通過仿真對前面的分析進行了驗證。仿真結果表明,基于文中模型的分析結果與實際情況吻合度較高,能夠較為準確地刻畫信道估計誤差對ZFBF傳輸速率性能的影響,通過這種近似,可以更方便地求得訓練序列的最優長度,為系統的設計提供參考。
[1] GESBERT D,KOUNTOURIS M,HEATH J R W,et al. From Single User to Multiuser Communications:Shifting theMIMOParadigm[J].IEEESig.Proc.Magazine,2007,24(5):36-46.
[2] COSTA M.Writing on Dirty Paper[J].IEEE Transactions on Information Theory,1983,29(3):439-441.
[3] YOO T,GOLDSMITH A.The Optimality of Multiantenna Broadcast Scheduling Using Zero-forcing Beamforming[J]. IEEE Journal on Selected Areas in Communications,2006,24(3):528-541.
[4] 趙 辰,劉應狀,朱光喜.VLST系統中ZF檢測算法的研究[J].無線電通信技術,2006,33(2):37-39.
[5] CAIRE Giuseppe,JINDAL Nihar,KOBAYASHI Mari,et al.Multiuser MIMO Achievable Rates with Downlink Training and Channel State Feedback[J].IEEE Transactions on Information Theory,2010,56(6):2 845-2 866.
[6] SHEN Hong,XU Wei,JIN Shi,et al.Joint Transmit and Receive Beamforming for Multiuser MIMO Downlinks With Channel Uncertainty[J].IEEE Transactions on Vehicular Technology,2014,63(5):2 319-2 335.
[7] KIM Haksoo,YUHeejung,LEEYongH.Limited Feedback for Multi-cell Zero-forcing Coordinated Beamforming in Time-varying Channels[J].IEEE Transactions on Vehicular Technology,2014,64(6):2 349-2 360.
[8] NI Wei,CHEN Zhuo,SUZUKI Hajime,et al.On the Performance of Semi-orthogonal User Selection with Limited Feedback[J].IEEE Communications Letters,2011,15 (12):1 359-1 361.
[9] MARZETTAT L.BLAST Training:Estimating Channel Characteristics for High Capacity Space-Time Wireless [C]∥Preceedings of the 37th Annu.Allerton Conf.Communication,Control,Computing,Monticello,1999:22-24.
[10]JINDALN.MIMO Broadcast Channels with Finite Rate Feedback[J].IEEE Transactions on Information.Theory,2006,52(11):5 045-5 060.
Analysis of Channel State Estimation Error’s Impact on ZFBF Sum Rate
LI Ning1,ZHANG Chao2,ZHAI Li-jun1,LIU Yun1
(1.The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China;2.School of Electronic Information and Communications,Huazhong University of Science and Technology,Wuhan Hubei 430074,China)
Zero-Forcing Beam-Forming is a simple downlink pre-coding algorithm for multi-user multi-input multi-output (MIMO)systems.It can approach the downlink capacity of multi-user MIMO when the user number is large enough.However,beam constructing relies on the precision of channel state information.In this paper,the sum rate loss caused by channel state estimation error is analyzed to form two approximations of sum rate.Then the optimal training sequence length is deduced in order to maximize the effective sum rate.Finally,the correctness and accuracy of the analysis are verified by simulations,and the result is useful for the design of practical systems.
MU-MIMO;ZFBF;channel estimation;optimal training sequence length
TN919.3
A
1003-3106(2016)05-0025-04
10.3969/j.issn.1003-3106.2016.05.07
2016-01-09
中國電子科技集團公司第五十四研究所發展基金資助項目(X1228156)。
李 寧 女,(1981—),博士,高級工程師。主要研究方向:無線通信與干擾管理。
翟立君 男,(1981—),博士,高級工程師。主要研究方向:衛星移動通信。

