超高速全并行快速傅里葉變換器

陳杰男 費 超 袁建生 曾維棋 盧 浩 胡劍浩

?

超高速全并行快速傅里葉變換器

陳杰男 費 超 袁建生 曾維棋 盧 浩 胡劍浩*

(電子科技大學通信抗干擾國家級重點實驗室 成都 611731)

設計和實現超高速快速傅里葉變換器(FFT)在雷達與未來無線通信等系統中具有重要意義。該文提出首個全并行架構的FFT處理器，其避免了復雜的路由尋址以及數據訪問沖突等問題，基于較大基進行分解降低運算復雜度。由于旋轉因子已知和固定，大量的乘法轉化為了定系數乘法。同時由于采用了串行的計算單元，在達到全并行結構的高速度同時硬件復雜度相對較低；所有的硬件計算單元處于滿載的條件，其硬件效率能達到100%。根據實際的實現結果，所提出的512點FFT處理器結構能夠達到5.97倍速度面積比的提升，同時硬件開銷僅占用了Xilinx V7-980t FPGA 30%的查找表資源與9%的寄存器資源。

快速傅里葉變換；全并行；比特串行計算；常系數乘法

1 引言

FFT(Fast Fourier Transform)作為技術核心之一廣泛應用于雷達以及無線通信領域。由于現有設計的吞吐率限制，系統中需要多個FFT單元協同處理。例如4G LTE(Long Term Evolution)中，需要近10套FFT以滿足信號接收、信道估計與均衡等處理需要；而在未來5G移動通信系統中，Massive MIMO(Multiple Input Multiple Output)接收端可能需要多達64~128路FFT支持。為滿足未來5G中低時延高吞吐率的需求，探究新的實現結構，以進一步提升FFT計算速度十分必要。

傳統FFT實現技術主要分為兩大類：基于流水線脈動結構與基于存儲器尋址結構。基于流水線的結構利用了FFT計算的規整性進行設計，但計算時間難以提升很難滿足未來高速處理需求。而基于存儲器的FFT處理結構普遍采用部分并行的策略來提升處理速度，但在面積上又有相應增加。

并行作為一種“面積換時間”的策略，可以從結構上提升系統吞吐率，但在FFT傳統實現方式中應用非常具有挑戰。首先點FFT需要至log2次復數乘法，并行帶來硬件復雜度較高。其次并行度提升后數據尋址、訪問與調度困難較大，數據沖突難以克服。為折中面積與處理速度，文獻[11]提出一種比特串行計算結構以面向低功耗場景。

在本文中，一種“結構全并行，計算基于比特級粒度”的FFT設計策略被提出，由全并行的結構得到較大的吞吐率提升，由串行化的計算單元縮減硬件面積。假設處理點字長為bit的FFT，全并行結構在一個時鐘得到全部點結果，而比特串行結構將這一個時鐘的計算分解到個時鐘。此外，全并行結構利用較大基分解以降低乘法數量，其固定的數據連線可以規避數據路由、尋址沖突等問題，固定的旋轉因子可以使用常系數乘法優化。關鍵路徑降低至加法器數量級，系統頻率得以提升。采用該設計方法的512點FFT處理器在Xilinx V7-980t上能夠達到9.931 GS/s的吞吐率，硬件開銷上LUT資源占總資源的30%，寄存器資源占9%。計算精度與16 bit定點FFT處理器相同，速度面積比是已有設計的5.97倍。

本文第2節介紹FFT分解算法；第3節闡明基于比特串行計算結構的全并行FFT實現；第4節給出主要結果與討論。

2 FFT分解算法

點離散傅里葉變換(DFT)以及旋轉因子表達式分別為

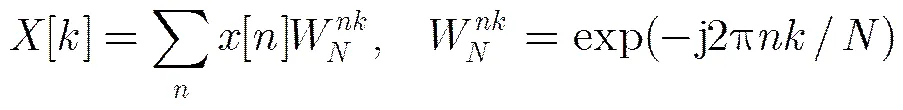
(2)

當分解因子不互質時，根據CTA算法[9]得(3)先進行1點FFT之后進行一次旋轉因子調整，之后再進行2點計算。

3 基于位串架構的全并行FFT設計

3.1 全并行FFT結構

如前文所述，FFT可以依據算法迭代分解，設分解為級，其中第級處理/N個N點FFT,，分解算法為CTA時需要進行旋轉因子調整，為PFA時只需要對數據進行合適連線。圖1所示為比特串行架構的64點全并行FFT示例圖，64點被分解為兩級8點FFT, 8點又被進一步分解為4點×2點。數據在每個時鐘分別逐比特輸入，其輸入順序按CTA算法排列。

圖1 64點全并行FFT結構示例圖

3.2 串行計算單元設計

如圖1中給出了基于比特串行的2點FFT運算單元示意圖。輸入0和1路在每個時鐘輸入一個比特。輸入1路的數據逐比特輸入串行乘法器，完成與旋轉因子的乘法后分別輸入到加法器和減法器；輸入0路數據輸入到流水乘法器延遲補償器，經過一定數量延遲后輸出。加法器和減法器串行完成兩路輸入相加及相減。位串加法器由全加器、進位寄存器與2-to-1 MUX構成。對字長為bit的輸入，最低位LSB首先進行計算，此時進位選擇為0，之后進位都連接寄存器輸出。下一個字輸入時依次循環。單比特減法器與加法器功能相似，只是將減數路取反，同時每個計算周期第一拍時鐘初始進位設為1，等效于對減數的二進制補碼取反再加1。

比特串行乘法器用于將串行輸入的數據與FFT旋轉因子完成乘法后再串行輸出。在不充分進行符號位拓展的情況下，二進制補碼乘法無法直接利用序列移位相加來計算，由文獻[12]，利用移位加形式以及部分積截斷可以實現常系數乘法。如圖2(a)所示，基于CSD數(1.0-01)CSD表示的常系數乘法的豎式表達式，其中“-”表示權重“-1”。其中為輸入二進制向量，0表示部分積。為避免溢出，二進制數相加時需要進行符號位拓展，在圖中用箭頭表示。為了保證信號表示位數相同，需要在每一步加法時截位，截去的位在圖中用框表示。串行乘法器實現如圖2(b)所示。移位器由寄存器與多路選通器構成，通過在不同時刻選通不同寄存器，在一個時鐘同時完成符號位拓展與結果截位。

圖2 常系數乘法器示例

4 設計結果與討論

4.1 基于較大基的分解算法

降低FFT運算復雜度的關鍵是降低旋轉因子乘法的復雜度。一次復數乘法需要3次實數乘法完成[12]；當旋轉因子, (=0,/4,/2, 3/4)時，旋轉因子乘法可以由加減法完成；當(=/8, 3/8, 5/8, 7/8)時，旋轉因子對應0.7071(±1±)，一次復數乘法只需要兩次實數乘法。當基于較大基分解時，分解可以向著旋轉因子復雜度降低的方向進行。如表1所示，512點采用不同基分解時所需旋轉因子乘法數。表中分解方式為32點乘16點時，32點分解如圖3(b)，可以看出采用較大基分解時乘法復雜度較低。

表1 512點不同分解方式所需乘法次數統計

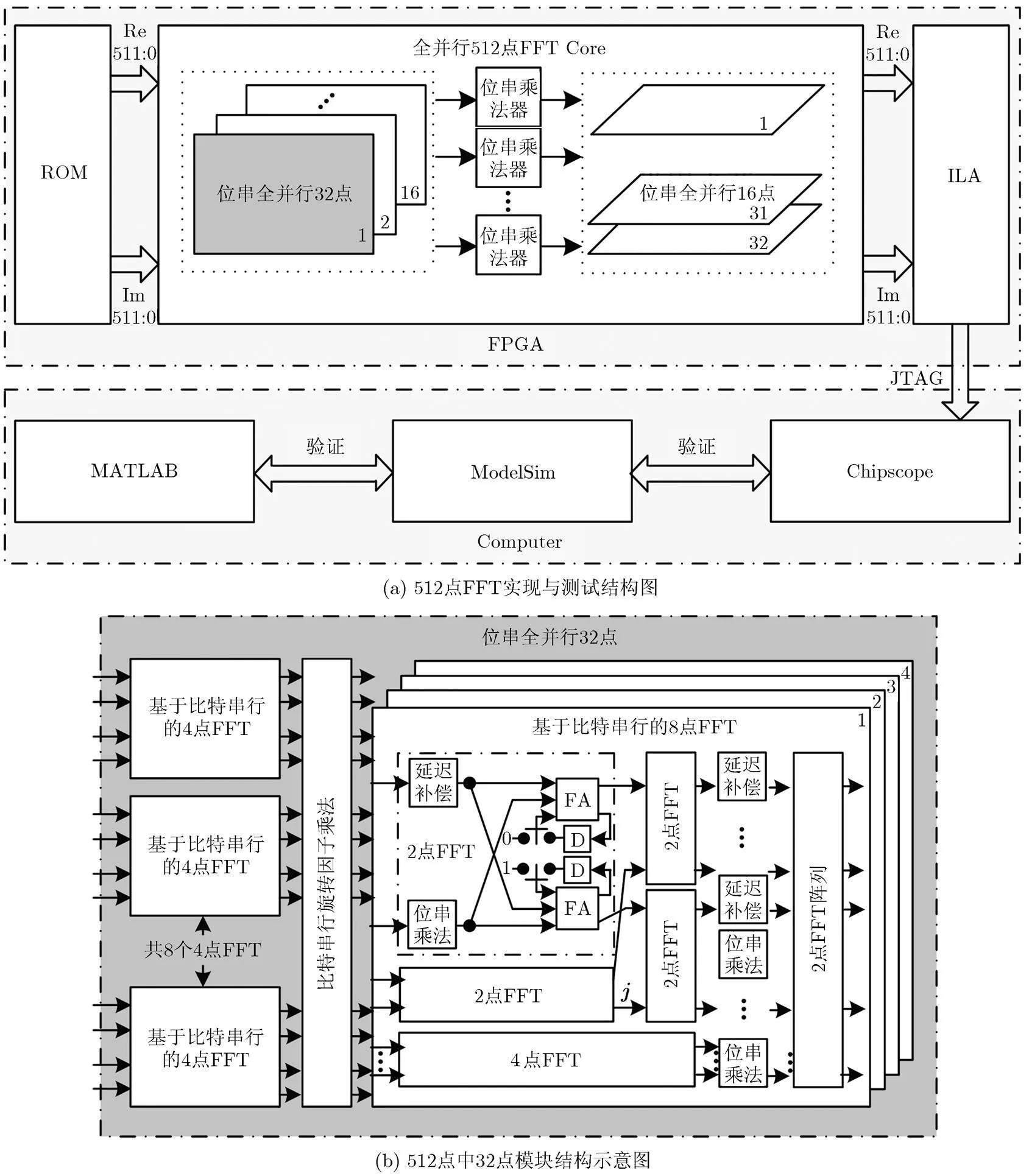
圖3 基于比特串行結構的全并行512點實現與測試

4.2 512點全并行結構實現與測試

512點全并行FFT的FPGA實現與測試結構如圖3(a)所示，FPGA測試在Xilinx FPGA Vertex-7vx980t上進行，向量存儲在ROM中，ROM輸出為IQ兩路，每路512 bit字長的數據。輸出采用了ILA核采集輸出信號，上載并與ModelSim以及Matlab對比驗證正確性。

4.3 FPGA實現結果與對比討論

實現結果如表2所示，在資源消耗上，全并行FFT占用了30%的查找表資源以及9%的寄存器資源；在處理性能上，處理器在16個時鐘得到全部512點結果，等效為32 Symbols/s，以報告的系統頻率310.348 MHz計算，系統可實現的吞吐率為9.931 GSymbol/s。表3給出了本文設計與已有文獻的結果比較。為了公平起見，以式(4)所定義的符號吞吐率除以等效邏輯門數量來衡量設計增益：

速度面積比=符號吞吐率/邏輯門數 (4)

表2本文設計的全并行結構資源消耗與性能細節

表3本文設計結構與已有文獻比對

如表3所示，由于定點字長有限，量化字長不同時，FFT輸出性噪比性能不同。采用先前文獻[6]中的測試方法，FFT輸入為加性高斯白噪聲信號，信噪比25 dB時，輸出信噪比在量化字長為12 bit時約為22 dB, 16 bit時約為23 dB。

由于采用了512點全并行的結構，本文結構相比較表中文獻[13]的設計，本文設計面積約是其4倍。同時，本文設計的符號吞吐率為文獻[13]的近27倍。在輸出信噪比性能一致的情況下，我們的設計其速度面積比為文獻[6]的近5.97倍。

5 結束語

本文提出一種應用于超高速大吞吐量要求的全并行FFT設計策略，基于“全并行結構比特串行”的方法。該設計通過在全并行的結構中串行化計算與存儲單比特串行；與已有設計方法相比較，本文的方法可以獲得更大的硬件效率和更高的吞吐率。

[1] 霍凱, 趙晶晶. OFDM新體制雷達研究現狀與發展趨勢[J]. 電子與信息學報, 2015, 37(11): 2776-2789. doi: 10.11999/ JEIT150335.

HUO Kai and ZHAO Jinjin. The development and prospect of the new OFDM radar[J].&, 2015, 37(11): 2776-2789. doi: 10. 11999/JEIT150335.

[2] 張洪倫, 巴曉輝, 陳杰, 等. 基于FFT的微弱GPS信號頻率精細估計[J]. 電子與信息學報, 2015, 37(9): 2132-2137. doi: 10.11999/JEIT150204.

ZHANG Honglun, BA Xiaohui, CHEN Jie,. FFT-based fine frequency estimation for weak GPS signal[J].&, 2015, 37(9): 2132-2137. doi: 10.11999/JEIT150204.

[3] 羅亞松, 許江湖, 胡洪寧, 等. 正交頻分復用傳輸速率最大化自適應水聲通信算法研究[J]. 電子與信息學報, 2015, 37(12): 2872-2876. doi: 10.11999/JEIT150440.

LUO Yasong, XU Jianghu, HU Hongning,. Research on self-adjusting OFDM underwater acoustic communication algorithm for transmission rate maximization[J].&, 2015, 37(12): 2872-2876. doi: 10.11999/JEIT150440.

[4] WANG Chao, YAN Yuwei, and FU Xiaoyu. A high- throughput low-complexity radix-24-22-23 FFT/IFFT processor with parallel and normal input/output order for IEEE 802.11ad systems[J]., 2015, 23(11): 2728-2732. doi: 10.1109/TVLSI.2014.2365586.

[5] YU Chu and YEN Mao-Hsu. Area-efficient 128-to 2048/ 1536-point pipeline FFT processor for LTE and mobile WiMAX systems[J]., 2014, 23(9): 1793-1800. doi: 10.1109/ TVLSI.2014.2350017.

[6] WANG Zeke, LIU Xue, HE Bingsheng,. A combined SDC-SDF architecture for normal I/O pipelined radix-2 FFT[J]., 2014, 23(5): 973-977. doi: 10.1109/TVLSI.2014. 2319335.

[7] CHEN Jienan, Hu Jianhao, and LEE Shuyang. High throughput and hardware efficient FFT architecture for LTE application[C]. IEEE Wireless Communications & Networking Conference. Shanghai, 2012: 826-831. doi: 10.1109/WCNC.2012.6214486.

[8] CHEN Jienan, HU Jianhao, LEE Shuyang,. Hardware efficient mixed radix-25/16/9 FFT for LTE systems[J]., 2015, 23(2): 221-229. doi: 10.1109/TVLSI.2014.2304834.

[9] COOLEY J W and TUKEY J W. An algorithm for the machine calculation of complex Fourier series[J]., 1965, 19(90): 297-301. doi: 10.2307/2003354.

[10] DUHAMEL P and VETTERLI M. Fast fourier transforms: a tutorial review and a state of the art[J]., 1990, 19(4): 259-299. doi: 10.1016/0165-1684(90)90158-U.

[11] YANG Lang and CHEN T W. A low power 64-point bit-serial FFT engine for implantable biomedical applications[C]. Euromicro Conference on Digital System Design, Funchal, Portugal, 2015: 383-389. doi: 10.1109/DSD.2015.30.

[12] PARHI K K. VLSI Digital Signal Processing Systems: Design and Implementation[M]. New York, USA, John Wiley & Sons, 1999: 490-499.

[13] MA Zhenguo, YIN Xiaobo, and YU Feng. A novel memory-based FFT architecture for real-valued signals based on radix-2 decimation-in-frequency algorithm[J].:,2015, 62(9): 876-880. doi: 10.1109/TCSII.2015.2435522.

An Ultra-high-speed Fully-parallel Fast Fourier Transform Design

CHEN Jienan FEI Chao YUAN Jiansheng ZENG Weiqi LU Hao HU Jianhao

(National Key Laboratory of Science and Technology on Communications, University of Electronic Science and Technology of China, Chengdu 611731, China)

The design and implementation of ultra-high-speed FFT processor is imperative in radar system and prospective wireless communication system. In this paper, the fully-parallel-architecture FFT with bit-serial arithmetic is proposed. This method avoids the complexity of data addressing, access and routing. Based on the high-radix factorization, the multiplication number can be reduced. Out of the reason that twiddle factors are fixed in the design, constant coefficient optimization can be used in multiplications. Besides, bit-serial arithmetic cuts down the hardware cost, and makes the computation elements full-load to get a 100% efficiency. As a result, the presented 512-point FFT processer has 5.97 times gain in speed-throughput ratio while its hardware only accounts for 30% LUTs and 9% registers resource based on Xilinx V7-980t FPGA.

Fast Fourier Transform (FFT); Full parallel; Bit-serialcalculation; Constant coefficient multiplication

TN47

A

1009-5896(2016)09-2410-05

10.11999/JEIT160036

2015-11-25；

2016-04-27；

2016-07-19

國家自然科學基金(6150010678, 61371104)

The National Natural Science Foundation of China (6150010678, 61371104)

胡劍浩 jhhu@uestc.edu.cn

陳杰男： 男，1986年生，副教授，研究方向為通信數字信號處理、超大規模集成電路設計與實現.

費 超： 男，1993年生，碩士生，研究方向為通信專用集成電路.

袁建生： 男，1992年生，碩士生，研究方向為通信與信息系統.