成敗型產品可靠性的Bayes驗收方案研究

劉海濤，張志華2，董理3

（1.海軍工程大學理學院，湖北武漢430033；2.海軍工程大學科研部，湖北武漢430033；3.海軍工程大學兵器工程系，湖北武漢430033）

成敗型產品可靠性的Bayes驗收方案研究

劉海濤1，張志華2，董理3

（1.海軍工程大學理學院，湖北武漢430033；2.海軍工程大學科研部，湖北武漢430033；3.海軍工程大學兵器工程系，湖北武漢430033）

針對成敗型產品生產定型階段的可靠性驗收問題，為了合理綜合利用產品定型階段以前的先驗信息，利用競爭失效方法建立了產品定型階段和批生產階段的可靠性信息轉換模型，進而確定了批產品生產可靠度的先驗分布。在此基礎上，給出了其后驗分布、風險的計算方法以及Bayes驗收方案的制定方法。實例分析表明，該方法能夠大大減少驗收試驗量，且方法穩健。

數理統計學；可靠性；驗收試驗；Bayes方法；成敗型產品；批生產

0 引言

產品可靠性驗收試驗是產品驗收階段的一項重要工作。在產品已通過定型并批準轉入批生產的情況下，可靠性驗收試驗的目的是通過在規定條件下進行試驗，確定批產品可靠性是否符合規定要求［1］。目前，產品可靠性驗收試驗方案主要可從國家和軍用標準中選取。但是，現有標準提供的試驗方案一般要求較大的試驗量，特別是對于許多技術復雜、造價昂貴、研制經費緊張的大型復雜產品，驗收試驗產生的費用往往難以承受，導致實施存在困難。

事實上，在大型產品的研制過程中，通常會進行環境應力篩選試驗和可靠性鑒定試驗等，因此，將產品定型階段的可靠性鑒定試驗信息作為批產品驗收的先驗信息可以大大減小試驗量。如文獻［2-3］利用可靠性鑒定試驗信息確定批產品失效率的先驗分布，分析了不同保證試驗方案的風險問題。文獻［4］針對裝備研制過程中存在多階段試驗信息的特點，提出一種變總體下的Bayes可靠性試驗鑒定方法。文獻［5］針對傳統Bayes方法對驗前信息和現場信息不加區分的缺點，提出一種融合多源驗前信息的成敗型產品可靠性評估模型。但是，上述方法對如何將不同研制階段的產品信息轉化為批產品的先驗信息討論較少。

實際上，可靠性鑒定試驗的主要目的是驗證產品的設計水平和零部件選用是否達到任務規定的要求。而在批生產過程中，生產工藝（材料的選用、生產設施、人員的操作技術與管理水平）等方面可能存在一定問題，因此在批生產階段特別是生產初期，批產品可靠度將低于定型可靠度。也就是說，批產品的可靠性是由其設計、零部件及生產工藝等因素決定的，而可靠性鑒定試驗主要是發現產品的設計和零部件缺陷，對生產工藝中存在的缺陷則無法充分考察［6-7］，因此，直接利用可靠性鑒定試驗信息確定批產品可靠度的先驗分布并不合理。針對這一問題，文獻［8］利用競爭失效模型建立產品定型階段和批生產階段的可靠性信息轉換模型，進而確定批產品失效率的先驗分布并對驗收試驗風險進行定量分析，但是該方法只針對指數分布進行了分析。

因此，本文以成敗型產品為研究對象，通過建立競爭失效模型對產品定型階段的試驗信息進行綜合，給出批產品可靠度的先驗分布。在此基礎上，對驗收試驗的風險進行分析，并給出驗收試驗方案的制定方法。

1 基于競爭失效模型的先驗分布確定

1.1競爭失效模型

由上文分析可知，批產品的失效機理可分為設計缺陷、零部件缺陷和工藝缺陷3種，其中任何一種機理的發生均會導致失效。因此，批產品失效實際是由設計缺陷、零部件缺陷和工藝缺陷共同組成的競爭失效模型。

而在產品研制階段，工程人員主要關注產品設計的合理性以及零部件缺陷，因此，研制階段的產品失效主要由設計缺陷和零部件缺陷引起。記pd、pc（0＜pd，pc＜1）分別為設計缺陷和零部件缺陷所引起產品失效的概率，則Rd=1-pd，Rc=1-pc分別為設計缺陷和零部件缺陷不引起產品失效的概率，稱其為設計可靠度和零部件可靠度。由競爭失效模型可知［9］，產品定型可靠度為

通過定型試驗的產品轉入批生產階段后，設pp為工藝缺陷所引起批產品失效的概率，則批產品的生產可靠度R［9］為

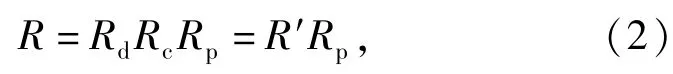
式中：Rp=1-pp為工藝缺陷不引起產品失效的概率，稱其為工藝可靠度，pp為工藝缺陷引起的產品失效概率。

由（2）式可知，批產品的生產可靠度R與定型可靠度R＇及工藝可靠度Rp有關。為了對批產品的生產可靠度R進行評估，可以首先對產品定型可靠度R＇和工藝可靠度Rp進行評估，然后利用（2）式得到批產品的生產可靠度R的評估結果。但是，工藝可靠度的評估往往比較困難，特別是在產品初期，可用于評估的信息非常少。

為此，對（2）式兩邊取對數，得到：

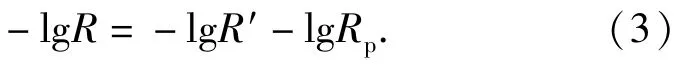
由此，可以定義比例系數ω為

對于（4）式，在產品可靠度較高的條件下，利用1階泰勒展開可以得到：

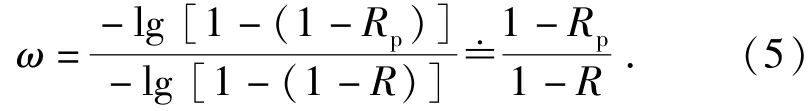
由于在試驗量為N時，N（1-Rp）實際上表示了由工藝缺陷所引起的失效個數，N（1-R）則表示了產品的總失效個數，因此，系數ω可近似表示因工藝缺陷引起產品失效占產品失效總數的比例，它綜合反映了批產品的生產工藝水平，可利用批產品的實際使用數據或專家經驗信息等確定。

由（3）式和（5）式可以得到：

1.2生產可靠度的先驗分布

由（6）式可知，為了得到生產可靠度R的先驗分布，需要確定定型可靠度R＇的先驗分布與系數ω.由于ω表示批產品因工藝缺陷造成產品失效占總失效數的比例，因此當批產品使用信息較多，可以較為準確地估計ω并將其作為常數處理；當批產品使用信息不多，即關于系數ω的信息較少時，可以將系數ω視為隨機變量，并利用掌握的先驗信息確定它的先驗分布。本文以將ω視為常數為例進行分析。

為了得到定型可靠度R＇的先驗分布，首先設分布形式為共軛先驗分布Beta（R＇|a0，b0），其密度函數為

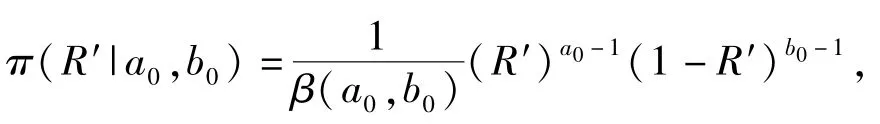
式中：a0、b0為超參數。

由于可靠性鑒定試驗可能采用一次抽樣檢驗、二次抽樣檢驗、多次抽樣檢驗以及序貫抽樣檢驗等不同方案，所得到的數據形式也不相同，因此，為敘述的統一起見，不妨從可靠性鑒定試驗的定型結論出發構造其先驗分布。

記可靠性鑒定試驗的定型結論為：1）在置信水平γ下，可靠度置信下限為R＇L；2）可靠度的點估計為則超參數a0、b0可利用下列方程組［10］求得

由此，利用（6）式和（7）式，在給定系數ω的情況下，可以得到批產品生產可靠度R的先驗分布為

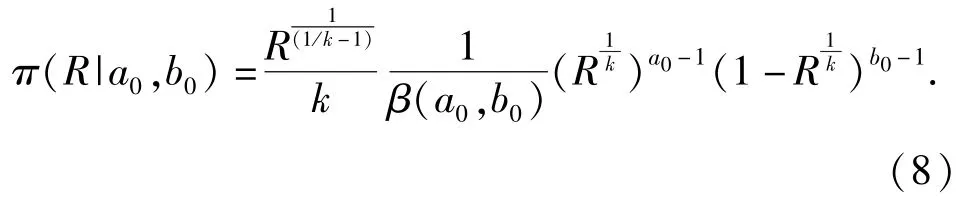
但是，（8）式所示的先驗分布在實際使用中并不方便。為了工程應用方便，使用 Beta分布Beta（R|a，b）作為先驗分布式（8）式的近似分布，即批產品生產可靠度R的先驗近似分布為Beta（R|a，b），此時參數a、b［7］滿足

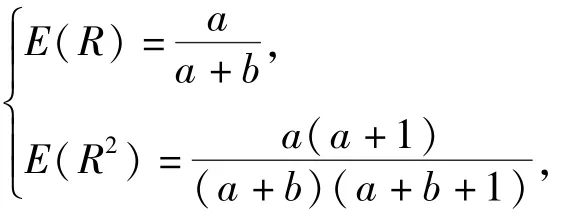
即

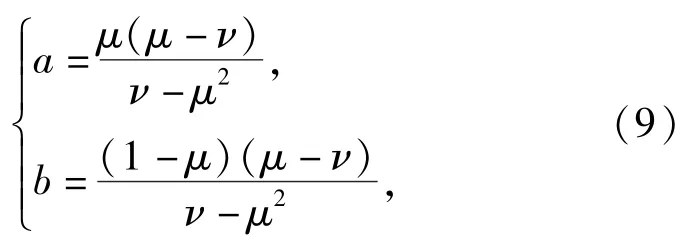
式中：μ、ν分別表示批產品生產可靠度R的1階矩和2階矩，即

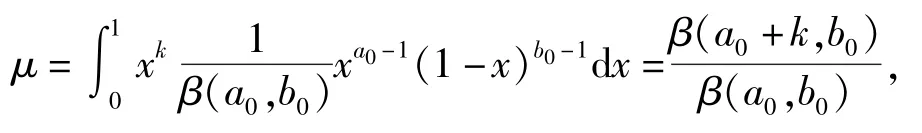
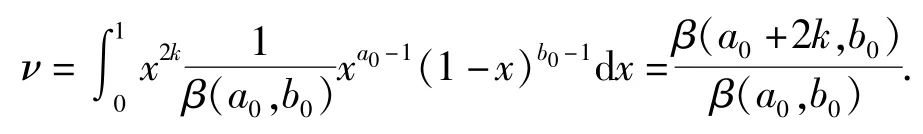
2 驗收方案的制定

2.1后驗分布的確定

對給定的批產品生產可靠度R的先驗分布Beta（R|a，b）和任一生產定型試驗結果（N，r），其后驗密度函數為

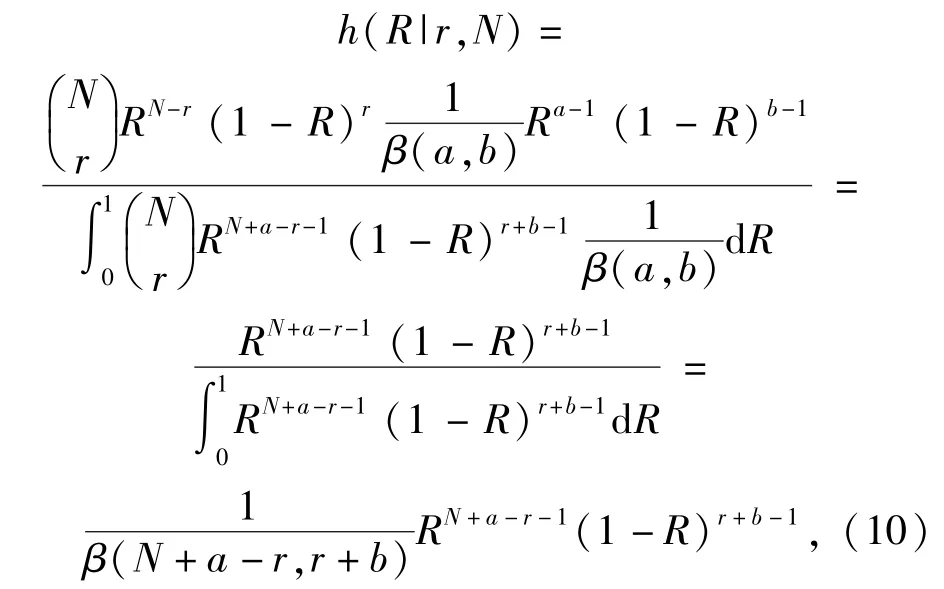
后驗概率為

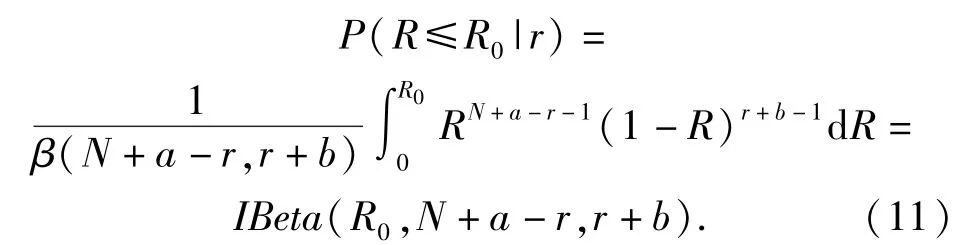
2.2風險分析

記合格質量水平為R0，對于生產方，其風險為合格產品沒有通過驗證試驗而被拒收的概率，即P（沒通過檢驗|R≥R0），也即

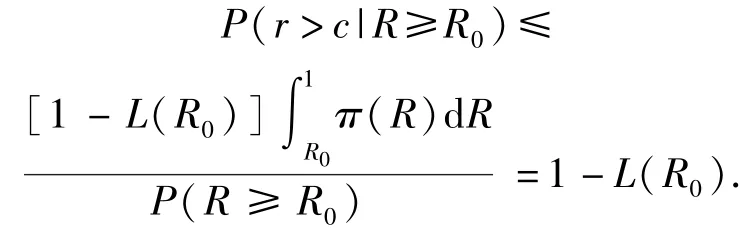
若給定生產方風險α，則只需要求

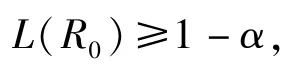
特別地

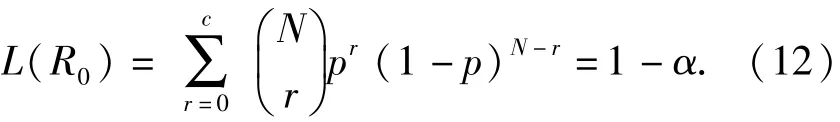
記極限質量水平為Rl，使用方風險為β，對于使用方而言，其風險為接收的產品為不合格產品的概率，即P（R≤Rl|通過檢驗），即

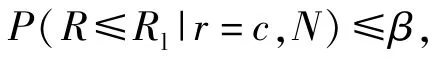
特別地

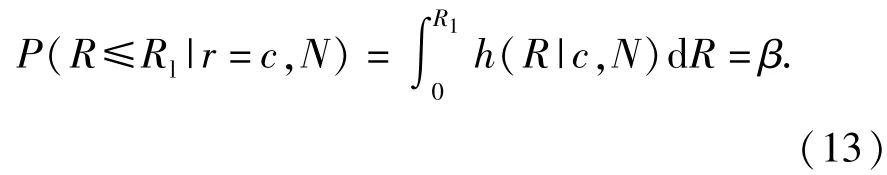
2.3方案的制定

綜上，只需要求制定的驗證試驗方案（N，c）滿足（12）式和（13）式的聯立方程組

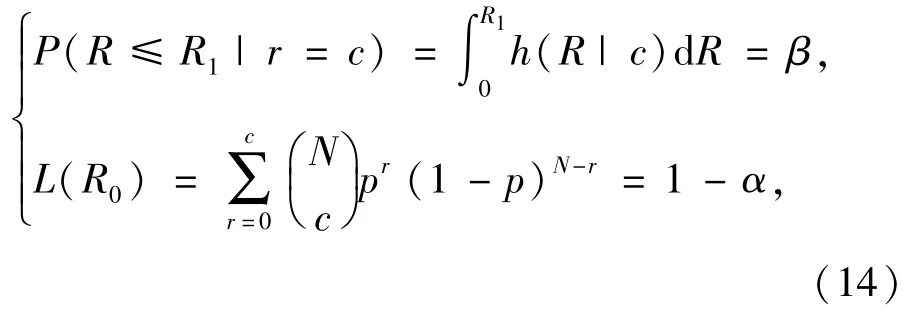
即可滿足生產與使用雙方對風險的要求，保證雙方的利益。其方案制定步驟為：

1）對給定的使用方風險β和產品可靠度的目標值Rl，利用（13）式求出總試驗次數N；

2）計算L（R0），如果（12）式不滿足（即達不到生產方可接受的要求），則在使用方允許的范圍內適當調整使用方風險β或合格質量水平R0。重復上述步驟。

3 實例分析

設某成敗型產品的合同書規定其任務可靠度為R0=0.999.綜合考慮生產方和使用方因素，確定其可靠性驗收試驗的相關參數為：合格質量水平R0= 0.999，鑒別比d=2.0；生產方風險α=30%；使用方風險取β=30%.同時，已知該產品在定型階段的可靠性鑒定試驗中共進行了648次試驗，均未發生失敗。

3.1經典驗收試驗方案

查閱國家標準GB5080.5—85，可以容易地獲得批產品的經典一次計數抽樣驗收試驗方案，如表1所示。

表1　某成敗型批產品可靠性驗收試驗的經典方案Tab.1 Classical reliability testing schemes for a batch of binominal products

3.2Bayes驗收試驗方案

由已知可靠性鑒定試驗數據（648，0），根據（9）式可以得到系數ω下生產可靠度R的先驗分布Beta（R|a，b），如表2所示，例如當ω=1/10時，代入（9）式可求得a=583.199 9，b=1.000 0.在已知批產品可靠度的先驗分布Beta（R|a，b）的情況下，由（10）式和（11）式可以得到批產品可靠度后驗密度函數和后驗概率。

然后按照2.3節驗收方案的制定步驟，可以得到相應的Bayes驗收試驗方案，如表2所示。其中，N0為失效數為0時的驗收方案，N1為失效數為1時的驗收方案，N2為失效數為2時的驗收方案，N3為失效數為3時的驗收方案。

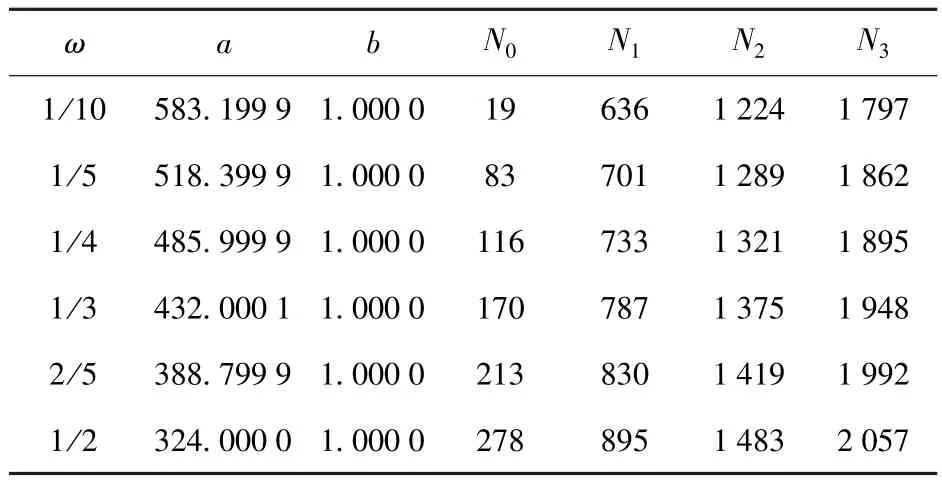
表2　某成敗型批產品可靠性Bayes驗收方案及相關參數Tab.2 Bayesian reliability testing schemes and parameters for a batch of binominal products

由表2可以看到，隨著ω的增大，也即工藝缺陷對產品的影響越來越大，驗收試驗量平穩地增大。例如，ω=1/4時的無失效方案為116，ω=1/3時的無失效方案為170，ω=2/5時的無失效方案為213，可見隨著工藝缺陷影響的增大，試驗量增加的幅度較為平穩，如從ω=1/4增加到ω=1/3時試驗量增加54，而從ω=1/3增加到ω=2/5時試驗量則增加43.

4 結論

對許多價值昂貴的大型復雜產品，傳統可靠性驗收方法所要求的試驗量過大，導致驗收方案難以實施。針對此問題，分析了成敗型產品可靠性的Bayes驗收方案制定問題，利用競爭失效模型對定型階段和批生產階段的可靠性信息進行合理綜合，在此基礎上，給出了其Bayes驗收方案的制定方法。實例分析表明，該方法具有較好的穩健性，且通過合理利用可靠性先驗信息，大大減少了驗收試驗量。下一步，可利用該思路進一步研究產品驗收可靠度的評估問題。

（References）

［1］ 張志華，田艷梅，郭尚峰.指數型產品可靠性驗收試驗方案研究［J］.系統工程與電子技術，2005，27（4）：753-756. ZHANG Zhi-hua，TIAN Yan-mei，GUO Shang-feng.Bayesian scheme of acceptance test in exponential case［J］.Systems Engineering and Electronics，2005，27（4）：753-756.（in Chinese）

［2］ 陳家鼎，張綃.關于MIL-HDBK-781中的保證試驗［J］.數理統計與管理，2000，19（2）：39-45. CHEN Jia-ding，ZHANG Xiao.On theassurance tests in MIL-HDBK-781［J］.Application of Statistics and Management，2000，19（2）：39-45.（in Chinese）

［3］ 洪國鈞，安偉光，劉玉明.平均故障時間保證試驗風險研究［J］.中國造船，2000，41（1）：73-81. HONG Guo-jun，AN Wei-guang，LIU yu-ming.Study on MTBF assurance test risks［J］.Shipbuilding of China，2000，41（1）：73-81.（in Chinese）

［4］ 邢云燕，武小悅.成敗型系統變總體下的Bayes可靠性試驗鑒定方法［J］.系統工程理論與實踐，2011，31（2）：323-327. XING Yun-yan，WU Xiao-yue.Bayesian reliability test evaluation for binomial system in varying population case［J］.Systems Engineering-Theory&Practice，2011，31（2）：323-327.（in Chinese）

［5］ 劉晗，郭波.融合多源驗前信息的成敗型產品可靠性Bayes評估［J］.彈箭與制導學報，2007，27（2）：338-341. LIU Han，GUO Bo.Fusion ofinformation of multiple sources in Bayesian assessment for reliability of success or failure product ［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2007，27（2）：338-341.（in Chinese）

［6］ 張詳坡，尚建忠，陳循，等.三參數Weibull分布競爭失效場合加速壽命試驗統計分析［J］.兵工學報，2013，34（12）：1603-1610. ZHANG Xiang-po，SHANG Jian-zhong，CHEN Xun，et al.Statistical inference of accelerated life test with competing failures based on three-parameter Weibull distribution［J］.Acta Armamentarii， 2013，34（12）：1603-1610.（in Chinese）

［7］ 張志華.可靠性理論及工程應用［M］.北京：科學出版社，2012. ZHANG Zhi-hua.Reliability theory and engineering applications ［M］.Beijing：Science Press，2012.（in Chinese）

［8］ 張志華.可靠性保證試驗的風險分析［J］.兵工學報，2006，27（6）：1060-1063. ZHANG Zhi-hua.Riskanalysis of reliability assurance test in the case of exponential distribution［J］.Acta Armamentarii，2006，27（6）：1060-1063.（in Chinese）

［9］ 張英芝，牛序磊，申桂香，等.基于競爭失效模式的數控機床可靠性建模［J］.系統工程理論與實踐，2014，34（8）：2144-2148. ZHANG Ying-zhi，NIU Xu-lei，SHEN Gui-xiang，et al.Numerically-controlled machine reliability modeling based on competing failure mode［J］.Systems Engineering-Theory&Practice，2014，34（8）：2144-2148.（in Chinese）

［10］ 徐志軍，張博，王凱，等.基于Beta分布的改進的一次可靠度法研究［J］.土木工程與管理學報，2014，31（3）：17-21. XU Zhi-jun，ZHANG Bo，WANG Kai，et al.Study of modified first order reliability method based on Beta distribution［J］.Journal of Civil Engineering and Management，2014，31（3）：17-21.（in Chinese）

Bayesian Acceptance Test Scheme for Reliability of Binomial Products

LIU Hai-tao1，ZHANG Zhi-hua2，DONG Li3
（1.College of Science，Naval University of Engineering，Wuhan 430033，Hubei，China；2.Office of Research&Development，Naval University of Engineering，Wuhan 430033，Hubei，China；3.Department of Weaponry Engineering，Naval University of Engineering，Wuhan 430033，Hubei，China）

For the acceptance test of binominal products in the production definition phase，an information transition model for type approval phase and batch production phase is established using competitionfailure method in order to properly use the prior information of the type approval phase.The prior distribution of batch products’reliability is presented.On this basis，the calculation method of posterior distribution and risk is given，and a Bayesian acceptance test scheme is proposed.The experimental results show that the proposed method can be used to enormously reduce the acceptance test，and has preferable stability.

mathematical statistics；reliability；acceptance test；Bayesian method；binominal product； batch production

O213.2

A

1000-1093（2016）03-0565-05

10.3969/j.issn.1000-1093.2016.03.025

2015-03-01

海軍工程大學自然科學基金項目（HGDQNEQJJ15002）；海軍工程大學社會科學基金項目（HGDSKJJ2015E10）

劉海濤（1982—），男，講師，博士。E-mail：liuhaitao0211@163.com