花園湖退洪閘閘墩混凝土施工淺析

淮河干流蚌埠～浮山段行洪區調整和建設工程施工X標花園湖退洪閘建筑安裝工程共有閘墩26個，順水流方向長18m，寬1.8m，高7.8m，采用常態混凝土澆筑，每次澆筑1個閘墩，一次性澆筑到頂，并在閘墩內布置冷卻水管，單墩混凝土方量約200m3。采用扣件鋼管支撐體系，搭設鋼管腳手架，排架頂部兩側各設1.5m高的欄桿，并搭設一斜挑，以方便人員上下施工。門槽采用二期混凝土。

一、施工工藝流程

腳手架搭設→掛樣架→豎墩墻側面模板→墩墻鋼筋綁扎→門槽模板安裝→另一側模板→圓頭模板安裝及整體加固→搭倉面挑→清理、沖倉驗收→澆筑混凝土→養護 。

二、模板的安裝與加固

由于工程量大、工期緊、質量要求高，模板的選材要在滿足清水混凝土要求的前提下，盡可能考慮降低成本。

（1）大面墻體采用鋼框竹膠板，即平面為2440 mm×1220 mm×18 mm的覆膜竹膠板，縱橫梁采用∠50×50×5mm的角鋼加工成框架；用φ8平頭螺絲將板與骨架拼裝成整體。

（2）墩頭圓形模板采用3mm厚的鋼板加工成定型模板。

（3）加固措施

利用2根φ48的鋼管作豎向龍骨，固定在樣架上，用10#槽鋼鉆孔，孔的位置與對銷螺栓相同，作橫向圍檁；用φ16鋼筋加工成對銷螺栓，中間穿以和混凝土斷面相同尺寸的黑鐵管，水平穿在兩邊橫向圍檁外，并用鐵板墊片加螺絲固緊，對銷螺絲的豎向間距為60cm，水平間距為60cm，模板與模板之間用φ10的螺絲連接，間距35cm。

（4）對拉螺栓間距驗算

振搗混凝土時產生的荷載標準值：按施工經驗對模板振搗荷載控制在 3～4kN/m2；

新澆混凝土對模板側壓力：

t°=200（t+15） （t為混凝土溫度）

γ—混凝土重度；

β1—外加劑影響修正系數，不摻加取1.0，摻具有緩凝作用的取1.2；

β2—混凝土坍落度影響修正系數，當坍落度小于30mm時取0.85，坍落度為50～90mm時取1.0，坍落度為110～150mm時取1.15。閘墩混凝土坍落度為50～70mm；

v—混凝土澆筑上升速度按1m/h計算；

傾倒混凝土時產生的荷載按采用串筒澆筑時對側模產生的水平荷載標準值：取2kN/m2。

新澆混凝土對模板側壓力：

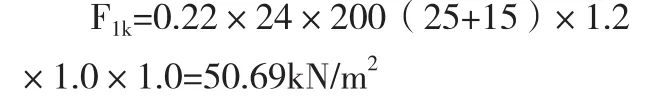
對拉螺栓受力面積為：

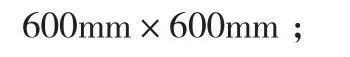
設計螺栓集中力為：

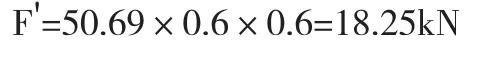
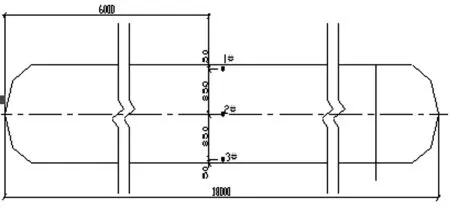
圖1 測點布置圖

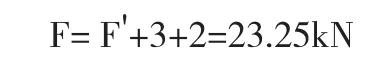
對拉螺栓采用φ16鋼筋，內徑1.355cm，截面積A=1.44cm2，鋼筋屈服強度σ=2400 kgf/cm2

螺栓能承受最大拉力：

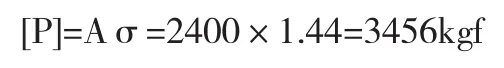
安全系數為：

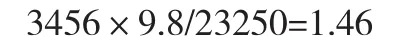
三、混凝土澆筑

常態混凝土澆筑采用4輛6m3混凝土攪拌車水平運輸， 2臺25t吊車配1m3吊罐（上下游各布置1臺）解決垂直運輸，一次性澆筑量約200m3，閘墩澆筑采用串筒入倉下料（共設6個下料點），串筒距混凝土澆筑面不超過2m，每層厚度0.5m，一次循環混凝土澆筑方量約16.2m3。

混凝土澆筑前在施工縫上，先鋪一層（厚2cm）比混凝土高一強度等級的水泥砂漿，混凝土澆筑采用人工平倉，用插入式軟軸振搗器振搗（布置5臺Φ70、1臺Φ50振搗器，其中1臺Φ70備用），振搗時按作用半徑均勻振搗，不漏振、不過振、不能撬碰模板，以保證振搗密實，模板不變形。

混凝土下料順序為從閘墩兩端向中間進行，避免泌水流向鋼模板側，倉面若出現泌水，在澆筑下批混凝土前，人工入倉排除。

鋼筋保護層墊塊隨混凝土澆筑上升的高度而跟著拆除，一方面防止混凝土表面收縮不均勻，另一方面保證混凝土外表美觀。

閘墩混凝土澆至設計高程后，在初凝后、終凝前采用二次壓光法施工。一方面可以消除混凝土表面干縮裂縫，另一方面提高閘墩表面的平整度和強度。

吊車均配1m3吊罐，計算時不計混凝土運輸及倒料時間，只計掛吊鉤時間10s；倉面卸料時間為15s；吊罐起升至9m高時即開始回轉至倉面需要的部位。全部操作過程均交叉進行，根據以往吊車澆筑混凝土的經驗資料，完成一次吊卸所需時間約5min。

每層混凝土澆筑時間驗算：

（1）澆筑每標準層混凝土需要時間：每層混凝土16.2m3，根據吊距不同，每次吊0.8 m3，需吊20次，每次需5min，共需約1.67h，配備2臺吊車僅需約0.83h，符合規范要求，不會形成冷縫。

四、冷卻水管布置

在閘墩內布置兩排冷卻水管（HDPE塑料管）間距0.8m，層高1.2m，長約160m，混凝土澆筑前并通水，通水流量為2m3/h，澆筑過程中注意觀察管道是否暢通，若不通，則對管道進行檢查疏通。通水7d。

五、溫度計埋設

混凝土澆筑過程中進行混凝土澆筑溫度的監測，在養護過程中還進行閘墩升降溫、內外溫差、降溫速度及環境溫度的監測，及時獲得反映閘墩混凝土內部溫度變化的實際情報所采取的施工技術措施的效果。

1.監測點的布置

閘墩混凝土溫度監測點的布置要能具有代表性，能真實地反映出混凝土里外溫差、降溫速度及環境溫度。即在閘墩的2m、6m的高度內布置測點如圖1。

2.監測頻率

澆筑后1～3d內每4h測溫一次，4～7d內每 6h測溫一次，8～15d內每12h測溫一次，15～28d內每24h測溫一次。

六、拆模

混凝土澆筑完成后3d開始拆除圓頭鋼模板，7d后開始拆除鋼框竹膠模板。

七、養護

要使混凝土在規定齡期內達到設計強度，必須做好養護工作。混凝土澆筑完成且頂部混凝土抹光后，用土工布進行覆蓋。閘墩兩端圓頭模板拆除后，用土工布進行包裹。待模板全部拆除完成后，澆水進行養護，養護時間不少于14d■