垂線站心坐標系中基于GNSS基線向量的高差計算
楊天宇 陳 強 王曉文
(四川省交通運輸廳公路規劃勘察設計研究院,四川成都 610041)
?
垂線站心坐標系中基于GNSS基線向量的高差計算
楊天宇陳強王曉文
(四川省交通運輸廳公路規劃勘察設計研究院,四川成都610041)
利用GNSS平差后的基線向量求解工程面內垂線站心直角坐標系中不同控制點之間的高差,按照距離定權的方式內插計算未知點的最終高程。當傳統的高程測量方法難以實施時,該方法具有實際意義。
垂線站心坐標系GNSS基線向量工程面坐標轉換高程
傳統的高差測量方法有水準測量和三角高程測量,前者精度高,但是勞動強度大;后者精度較低,一般僅能用于三等以下高程控制網的測量。兩種方法在霧天無法實施,對測量環境都有著較高的要求。在地形復雜的區域,如果仍然采用這兩種方法,會造成人力物力等成本的大幅增加;且在滑坡等危險地段,長時間的停留會對工作人員及儀器的安全造成巨大威脅。GNSS以其高精度、全天候、易選點等優勢受到了越來越多的歡迎,GNSS測量也已經在大地測量、變形監測、工程測量等多個領域得到了廣泛的應用[1]。筆者對小范圍內GNSS高差測量的可行性進行了探討,討論在地形復雜的區域以此方法替代傳統方法進行高差測量的可行性。
在小范圍內的工程面上可以不考慮地球曲率的影響,此時工程平面坐標系與高程坐標系統可以認為是相互垂直的,二者構成工程面內的垂線站心直角坐標系o-xyH,而GNSS基線向量所在的坐標系為地心直角坐標系O-XYZ,兩個坐標系之間可以進行轉換。通過GNSS基線向量的轉換得到工程面內已知高程點和未知高程點之間的高差,進而得到未知高程點的高程。
1 垂線站心直角坐標系
如圖1所示,以測站O為原點,O點的垂線為H軸(指向天頂為正),子午線方向為x軸(向北為正),y軸與x,H軸垂直(向東為正)構成左手坐標系。這個坐標系就被稱為垂線站心直角坐標系,也可以稱為站心天文坐標系。圖1中的O-XYZ為地心直角坐標系[2]。
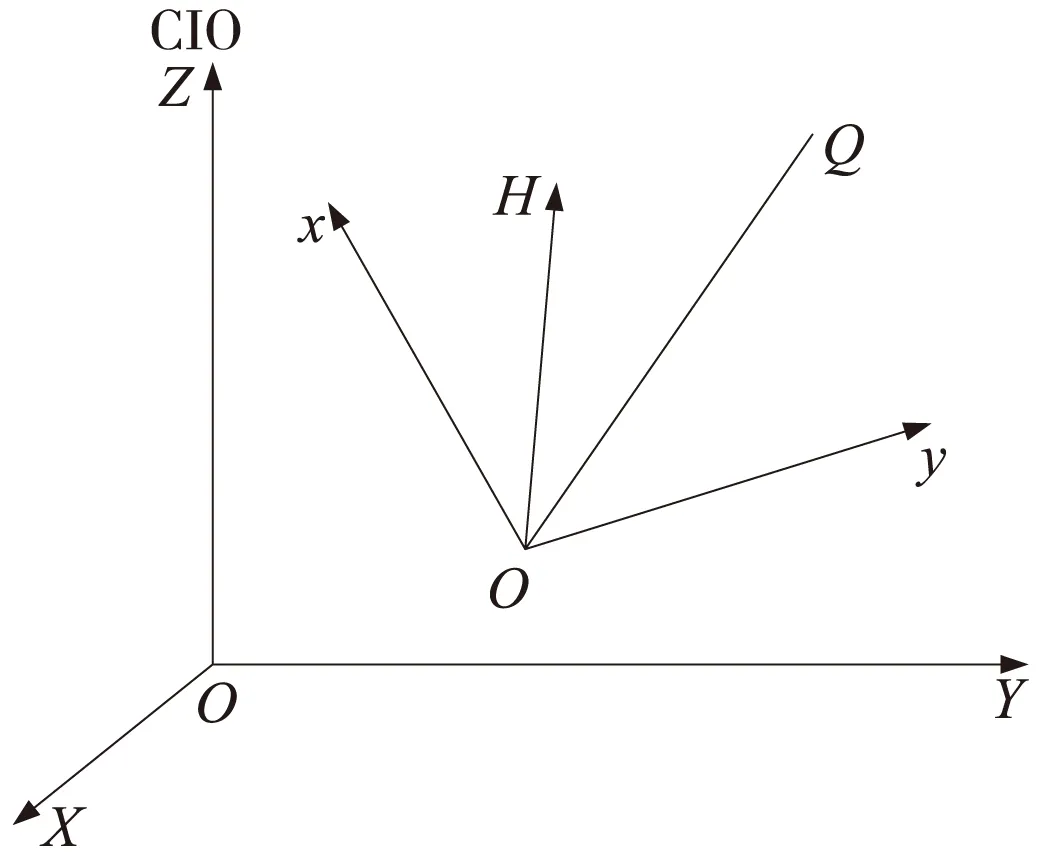
圖1 垂線站心直角坐標系
設O點的經緯度為(λ,φ),則Q點在兩個坐標系中關系為
(1)

根據該轉換矩陣,利用GNSS基線向量便可以得到在垂線站心直角坐標系下Q相對于O的坐標及高程。
2 基于GNSS基線向量的高差計算
如圖2所示為一個工程區域內的控制網示意,高程方向垂直向外,A、B、C點的高程已知,分別為HA,HB,HC。
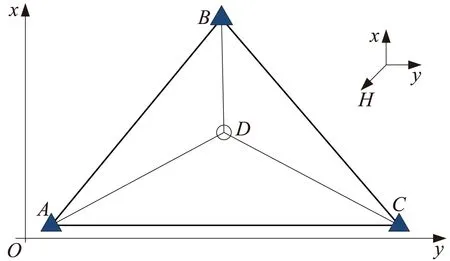
圖2 工程控制網示意
使用四臺GNSS儀器在4個點上同步測量,并對測量數據進行GNSS解算,得到合格的GNSS基線向量文件;然后再使用GNSS平差軟件進行GNSS基線向量文件的檢查,當閉合環限差滿足規范要求之后,進行三維平差,得到平差后的基線向量。
公式(1)是對坐標差進行轉換,只需要得到平差后的各基線坐標分量即可。同時從GNSS平差結果中獲取A點的經緯度,用于計算旋轉矩陣。根據(1)式可得
(2)

根據(2)式便可以計算出垂線站心直角坐標系中任意兩個點的坐標差及高差,進而計算出未知點的高程。
3 實例分析
以一個實際工程控制網為例(如圖2),控制點高程如表1所示,采用獨立的高程系統,表2為GNSS基線向量。

表1 控制點高程
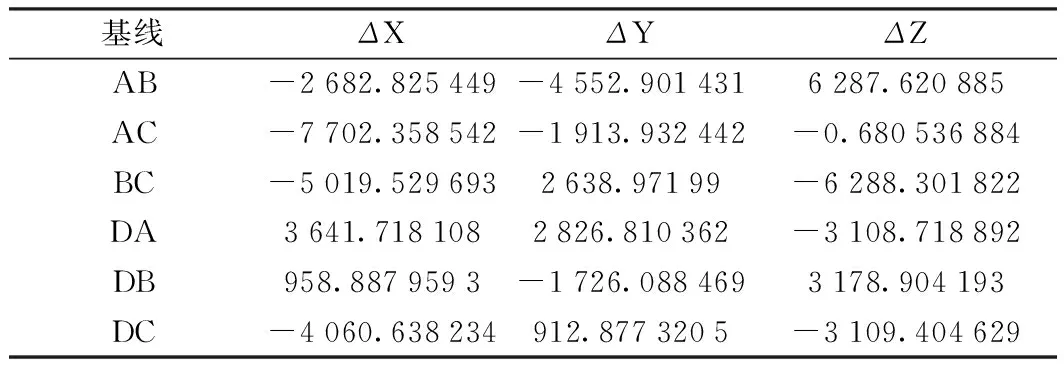
表2 GNSS基線向量 m
通過表2中的基線向量,結合由A點經緯度得到的旋轉矩陣,可以計算出B、C、D三個點相對于A點的高差;同理也可以由B、C點的經緯度確定不同的旋轉矩陣,得到A、C、D相對于B點,或者A、B、D相對于C點的高差。以A點經緯度計算得到的旋轉矩陣對GNSS坐標分量進行轉換,得到任意兩點之間的高差(見表3)。
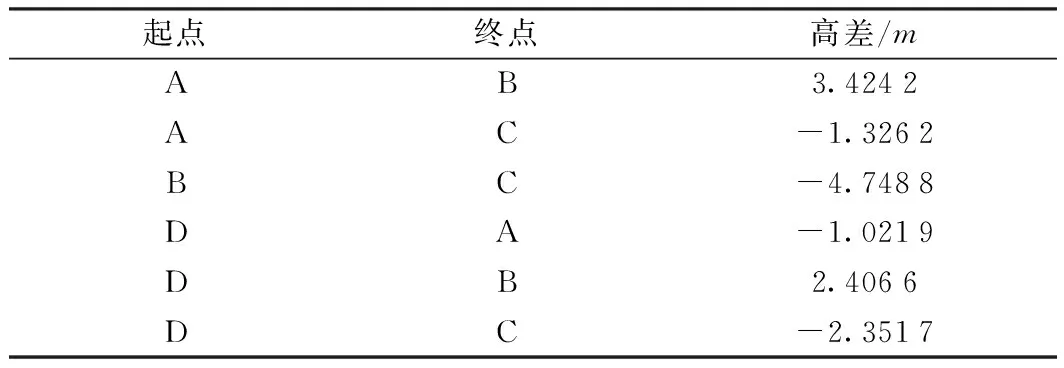
表3 垂線站心直角坐標系下任意兩點間高差
從表3中可以看出,不僅可以得到D點與已知高程點的高差,還可以得到已知點之間的高差,高差不符值如表4所示。
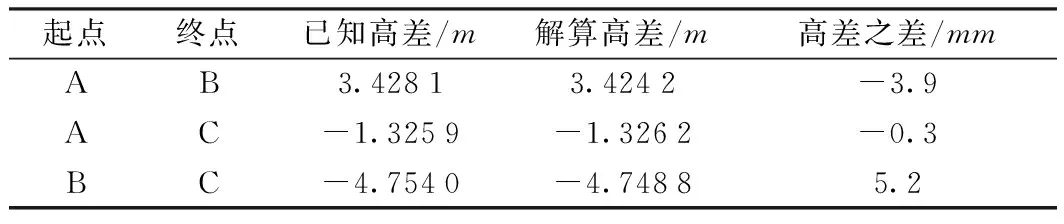
表4 檢測已知點高差
將GNSS與水準測量的結果進行對比,結果見表5。

表5 GNSS與水準測量結果對比 m
從表5可以看出,兩種方法測量D點高程較差為-6.5mm≤30.0mm(四等水準測量“檢測已測測段高差之差”的限差);在較小工程面內,當傳統高程測量方法不宜實施而且高程控制網等級要求不高時,可以利用GNSS法代替相應等級水準測量。
另外,根據表3中D點到A、B、C三個點的高差可以計算出未知點D的高程,分別為H1,H2,H3。為了得到更加合理的D點高程,可利用3個不同的D點高程,按照A、B、C到D點的距離內插計算得到最終的D點高程。設A、B、C到D點的距離分別為SAD,SBD,SCD,則D點高程為
(3)
4 結論
從理論分析和實例計算可知,在較小工程區域內,利用GNSS基線向量轉換的方法可以得到未知點與已知點之間的高差;根據不同已知高程點到未知點的距離,按照內插的方法進行加權平均計算,可以得到更加合理、可靠的未知點高程,其精度在一定條件下可達到四等或更高等級水準測量精度要求,值得相關工程參考采用。
[1]趙超英,張勤,王利.GNSS高差在滑坡監測中的應用研究[J].測繪通報,2005(1):39-41
[2]孔祥元.大地測量學基礎[M].武漢:武漢大學出版社,2010
[3]李志超,賈雷曉,李時華.傳統高程測量方法與GNSS高程測量的比較分析[J].山西建筑,2013,39(12):192-193
[4]方斌.GNSS高程在小面積工程測繪中的應用[J].山西建筑,2008,34(22):349-350
[5]趙超英,張勤,王利.GNSS高差在滑坡監測中的應用研究[J].測繪通報,2005(1):39-41
[6]曾云,胡友健.GNSS短基線測量的誤差來源[J].城市勘測,2004(2):18-21
[7]彭文廣,劉顯揚,黃忠枚.GNSS大地高高差代替水準高差在長江上游環境監測中的應用[J].科技信息:學術研究,2007(22)
[8]汪族仁.GNSS高程測量的研究和應用[J].工程與建設,2013,27(2):178-179
[9]蘭虎彪,王昆杰.GNSS網正常高求解方法的研究[J].武漢大學學報:信息科學版,1992(3):18-26
Calculation of Height Difference Based on GNSS Baseline in Topocentric Coordinate System for Perpendicular Line
YANG TianyuCHEN QiangWANG Xiaowen
2016-04-13
楊天宇(1980—),男,2006年畢業于西南交通大學大地測量學與測量工程專業,碩士,高級工程師。
1672-7479(2016)04-0007-02
P228
B

