用于電能質量預測分析的交流電弧爐時變參數模型

廖延濤胡　駿張海龍王恩榮

（1. 南京師范大學電氣與自動化工程學院，南京　210042；2. 南京師范大學物理科學與技術學院，南京　210023）

?

用于電能質量預測分析的交流電弧爐時變參數模型

廖延濤1胡駿1張海龍2王恩榮1

（1. 南京師范大學電氣與自動化工程學院，南京210042；2. 南京師范大學物理科學與技術學院，南京210023）

基于能量守恒定律建立了一種以微分方程描述的交流電弧爐（EAF）時域模型，模型以電弧導納作為狀態變量，電弧電流和弧長作為輸入，進一步根據弧長與電弧電壓關系式推導出模型參數與弧長的關系，并給出時變參數的工程估算方法。以實際煉鋼交流電弧爐為例，將帶通白噪聲信號疊加在弧長上模擬實際工況，分別對熔化期和精煉期電弧爐的動態特性以及電網的電壓波動和諧波進行仿真研究，仿真結果與實測數據相吻合，證明了模型的有效性和實用性。

電弧爐；電弧阻抗；時變參數；電能質量；負荷建模

交流電弧爐作為一種沖擊性的非線性負荷，對供電網絡造成了種種負面影響，包括諧波、電壓波動和閃變、三相不平衡以及有功沖擊和無功沖擊等電網污染，這對于電力系統的安全穩定運行是極為不利的［1-3］。

為了分析并解決上述由交流電弧爐引起的電網污染問題，建立精確、實用的交流電弧爐數學模型至關重要［4］。近年來，許多國內外學者對交流電弧爐的建模問題進行了大量研究［5-14］。通過實際電弧U-I特性曲線擬合的方法是目前應用較多、研究較為深入的方法［5-6］。該方法原理直觀明了，所需參數易于獲取，可用于諧波和電壓波動等電能質量的研究。但該模型依賴于負載消耗的實際有功功率，由于不同電弧爐的特性多樣性，參數難以準確地預估，仿真結果未免引入較大誤差，并且沒有考慮電弧的物理特征，無法體現弧長的隨機變化是導致電壓波動的根本原因［7］。基于能量平衡關系建立的動態電弧模型能夠從系統的運行環境和電弧的微觀變化上反映出電弧爐的實際動態特性［8-11］。模型從電弧的內在因素出發推導外部特性，將電弧作為一種非線性時變的電路元件接入供電系統仿真，能夠分析不同電弧爐引起的電能質量問題，具有較高的準確性和通用性。但由于模型參數的取值沒有明確的物理依據，往往需要依靠經驗或實測數據辨識，因此不適用于工程預測。文獻［12］基于電弧熱學原理，將電弧等效為非線性時變電阻，建立了電弧爐時變電阻模型。模型中的每個參數都有明確的物理意義，對于吻合實際電弧爐的運行特性有直觀的優勢，但研究對象一般為噸位較小的電弧爐。另有諸多文獻采用實測數據注入模型的方法對電弧爐引起的電能質量問題進行了深入研究［13-14］。然而，電弧爐作為一種時變系統，電弧具有高度的隨機性和時變性，模型參數的取值應當隨著弧長時刻變化，這在目前已報道的模型中并沒有得到體現。

鑒于此，本文提出一種模型參數隨弧長時序變化，適用于電能質量分析和工程預測的交流電弧爐模型。模型基于能量守恒定律建立，利用電弧爐系統的初始設計參數以及電弧的時變特點確定模型參數的估算方法，以避免傳統模型依賴實測數據辨識以及采用固定參數來模擬電弧爐時變系統的不足。通過實際煉鋼電弧爐為例進行仿真，以驗證模型的有效性以及對于電網電能質量預測分析的準確性。

1　模型建立與參數估計

1.1模型建立

如圖1所示為三相交流電弧爐電氣系統示意圖，鋼廠主變壓器將高壓電網電壓降壓后接入爐用變壓器一次側，然后通過短網輸送低電壓大電流至電極，從而產生電弧。

圖1　三相交流電弧爐電氣系統示意圖

由能量平衡原理可得

式中，q為電弧弧柱中積累的能量；u為電弧電壓；i為電弧電流；S0是電弧弧柱的視在功率損失。

將模型表示成導納的形式，式（1）轉化為

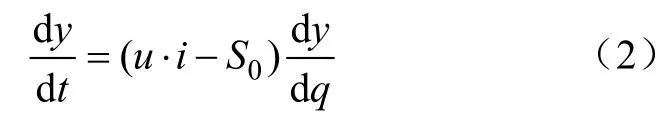
式中，y為電弧導納。

根據氣體分子運動論，得到電弧弧柱中積累的能量為［15］

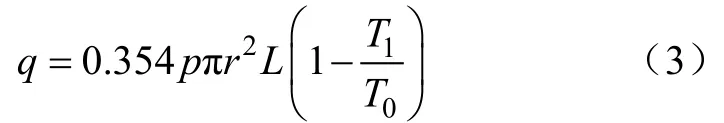
由沙哈公式推導出電弧電導率方程為

式中，σ為電弧電導率；σ0、m為常數，m取值為1.6014×104K［16］。

根據式（4）可推得電弧導納y為

將式（3）至式（5）代入式（2），整理得

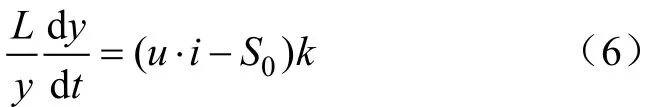
式中，參數k的表達式為

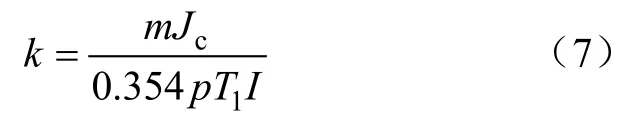
電弧損失的視在功率與電弧導納的關系式為

式中，Uarc是電弧電壓有效值。

將式（8）代入式（6），整理得

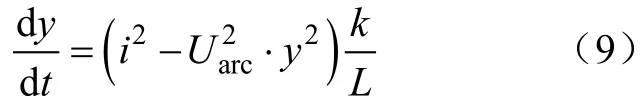
1.2參數估計

圖2所示為電弧爐單相等效電路圖，其中 Up表示電弧爐變壓器與檔位電壓對應的相電壓，rt為變壓器內部電阻，Lt為變壓器內部電感，rd為短網電阻，LdM為短網電感，Zarc為電弧阻抗。

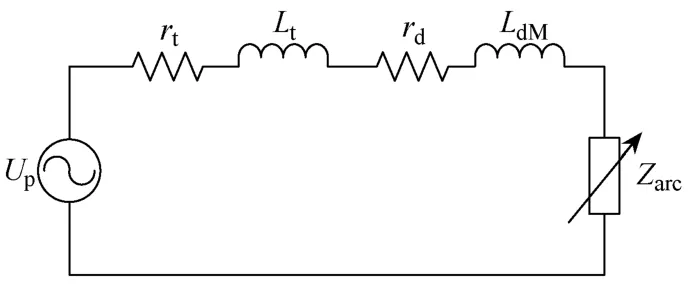
圖2　電弧爐單相等效電路圖

當電流大于 100A時，電弧電壓有效值 Uarc與電弧長度L的關系可以表示為［17］

式中，α為電弧陽極和陰極的電位降；β為弧柱梯度，α和β的值取決于電弧爐的冶煉時期［18］。

對于圖2，根據歐姆定律可得

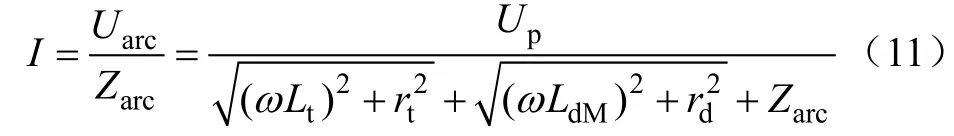
式中，I為電弧電流有效值；ω為供電電壓的角頻率。

結合式（10）和式（11），進一步推導出電弧電流有效值與弧長之間的關系如下

結合式（9）至式（12）得到提出的交流電弧爐時變參數模型為

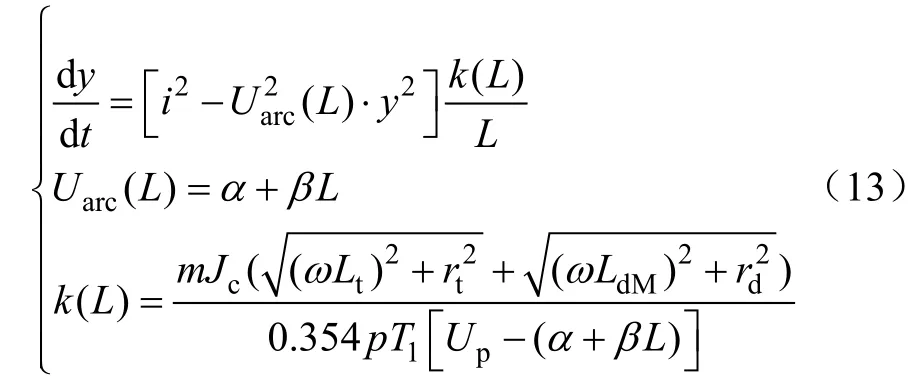
可以看出，模型參數Uarc（L）和k（L）均與L相關，Uarc（L）體現了弧長與電弧電壓的關系，而弧長與電弧電流、電弧半徑的關系隱含在k（L）中。隨著L的瞬時變化，模型參數也時刻變化，所描述的電弧伏安特性應當更加契合實際冶煉工況下的伏安特性，這正是本文提出時變參數模型的創新之處。同時，該模型還具有參數少且求解簡便的優點，重要的是模型參數不依賴于現場數據采樣辨識，從而具有更優異的普適性。

2　算例分析

以某鋼廠 40t電弧爐為例［11］，根據系統的實際參數，分別就熔化期和精煉期對電弧爐系統進行仿真，并將仿真結果與鋼廠提供的實測數據進行對比。如圖3所示，根據式（13）建立電弧仿真模型，進一步建立供電系統仿真模型。系統參數為：鋼廠主變壓器將110kV的高壓電網電壓變為35kV，低壓側電路等效阻抗為0.256Ω，通過爐用變壓器將電壓降到420V，短網電阻為0.4mΩ，短網電抗為2.496mΩ，鋼廠主變壓器的額定容量為63MVA，爐用變壓器的額定容量為22MVA，內部電阻為0.069mΩ，內部電感為0.0022mH。

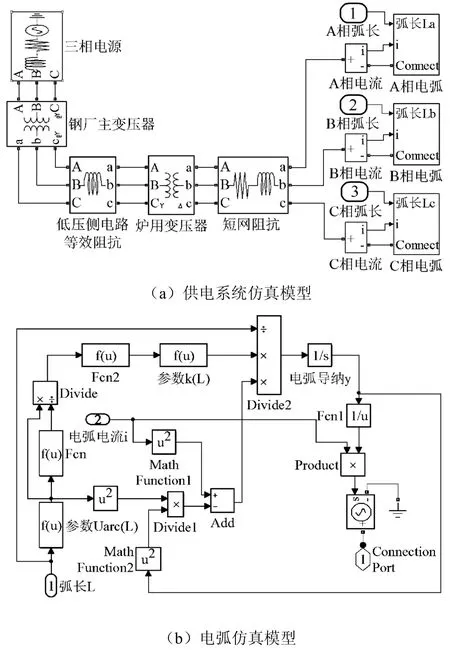
圖3　三相交流電弧爐電氣系統仿真模型

在實際運行中，由于受電磁力和爐料移動等因素影響，弧長的變化呈現出復雜的隨機特性，在不同的冶煉時期由于功率需求不同，其弧長變化范圍也不同。熔化期的弧長波動劇烈，形狀呈細長狀，而精煉期的弧長波動相對穩定，形狀呈短粗狀［18］。本文采用在最大弧長基礎上疊加帶通白噪聲信號的方法來模擬不同冶煉時期弧長變化的隨機性，計算表達式為

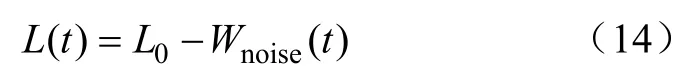
式中，L0=（Up?α）/β為最大弧長；Wnoise（t）為帶通白噪聲，頻率范圍選取4～14Hz［19］。

2.1熔化期運行特性

在熔化期，由于電弧一般較細長，并且爐溫較低，所以電弧不易穩定，弧阻抗的非線性較強，電弧電壓和電流波動較劇烈，對電網造成的電壓波動和諧波也較為顯著，由于維持長弧所需的能量更多，所以燃弧電壓和熄弧電壓都較高。根據文獻［18］中關于電弧電位分布的研究成果，α取值為40V，β取值為10V/cm，爐溫設為1150K，參照式（14）計算出熔化期弧長的理論波動范圍為0～20.25cm。本文暫不考慮極端工況，將弧長波動范圍選取為12～20cm［20］，如表1所示，Uarc（L）和k（L）分別在160～240V和0.2507～8.275cm·W-1·s-1范圍內隨機變化并且在時序上是連續的。

表1　不同冶煉時期的電弧爐模型參數比較

根據電弧爐的動態特性，驗證所提出模型的準確性，觀察指標選為電弧電流、電弧電壓以及電弧伏安特性，如圖4所示，弧長的變化導致電弧電流和電弧電壓劇烈波動，電流過零點處的伏安特性曲線傾斜度高，電流變化緩慢，“零休”現象明顯，即此時電弧的非線性較強，說明本文提出的時變參數模型能夠準確地模擬熔化期的電弧特性。

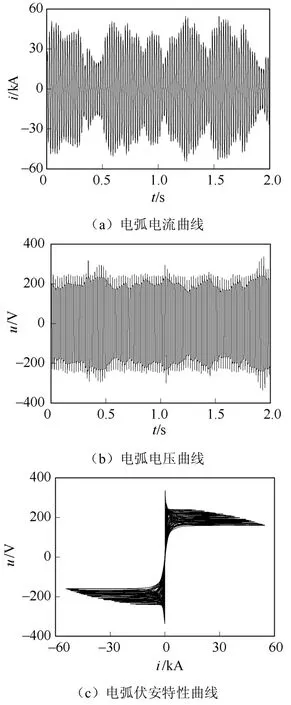
圖4　熔化期電弧爐的動態特性

進一步觀察電弧爐引起的電網電壓波動以及諧波，以驗證模型的實用性。國標GB/T 12326—2008《電能質量電壓波動和閃變》中給出的電壓波動d的定義表達式為

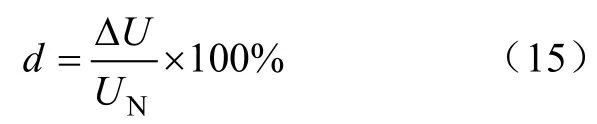
式中，ΔU為電壓方均根值曲線上相臨兩個極值之差；UN為系統標稱電壓。

如圖5所示，依據仿真得到的35kV母線上電壓Ud的數據，應用式（15）計算電壓波動，得到最大電壓波動值為3.47%，超出國標限值的3%，與實測值3.3%基本一致。

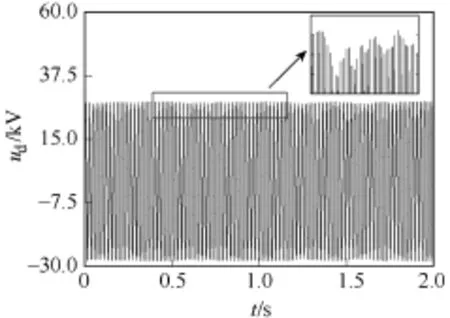
圖5　熔化期35kV母線A相電壓曲線

從表2可看出，熔化期諧波電流的仿真結果與實測數據比較，兩者不僅整體趨勢一致，從定量的角度觀察，也比較接近，尤其是2次諧波和各奇次諧波，誤差較小。根據國標GB/T 14549—1993《電能質量公用電網諧波》中公布的諧波電流允許值，5次和7次諧波電流超出國標允許值12A和8.8A，在接入電網前需要治理。

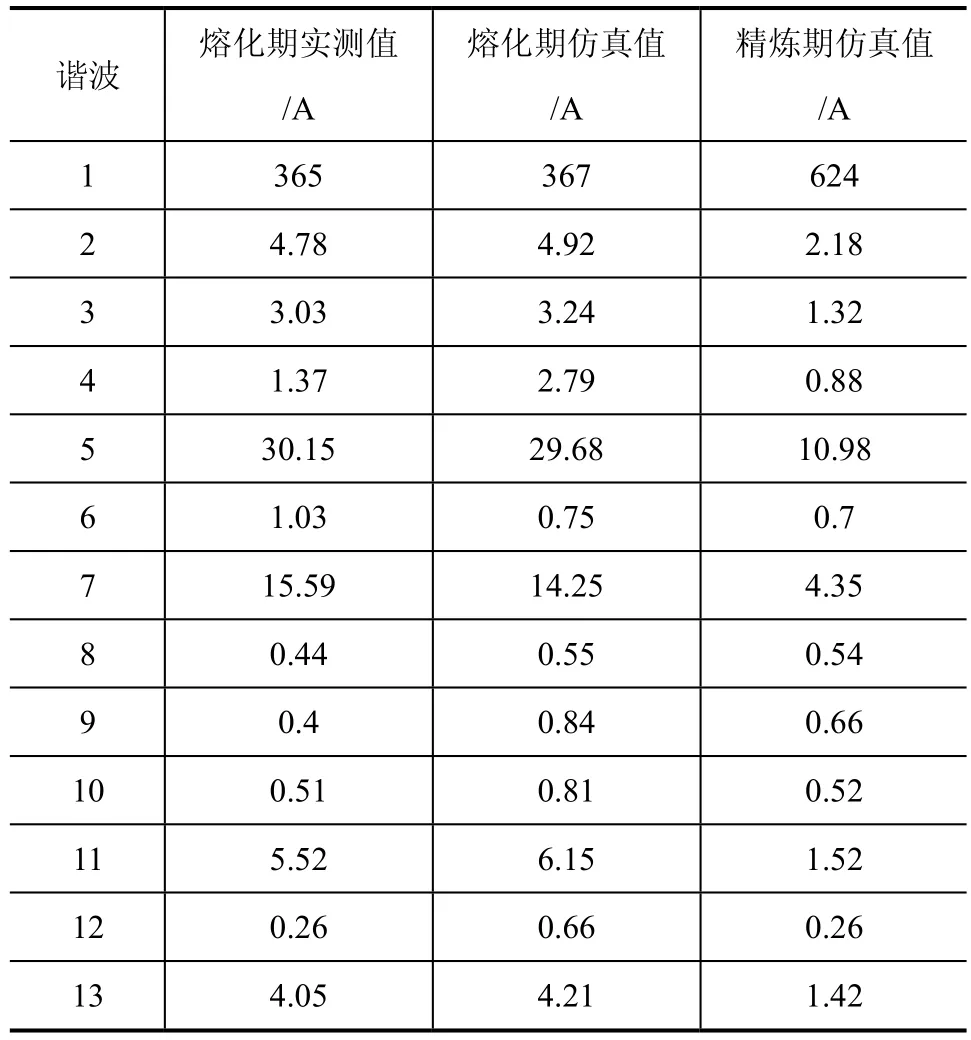
表2　35kV母線A相諧波電流分析結果

2.2精煉期運行特性

在精煉期，電弧呈短粗狀，爐溫升高，電弧趨于穩定，弧阻抗的非線性降低，電弧電壓和電弧電流比較穩定，引起的電網電壓波動和諧波也較小，由于維持短弧所需的能量少，所以燃弧電壓和熄弧電壓都很低。根據文獻［18］，α取值為20V，β取值為5V/cm，爐溫設為1800K，將弧長變化范圍選為8～10cm［20］。從表1中可以看出，當弧長波動呈現出不同的劇烈程度和趨勢時，參數也呈現出與熔化期不同的隨機特性。由式（13）可知，Uarc（L）和k（L）與弧長呈負相關，弧長降低必然導致二者數值下降。實際物理含義為：由于弧長降低，維持電弧所需的能量減少，從而導致電弧電壓有效值 Uarc（L）降低；而電流增大，電弧半徑增加，爐溫升高，也必然導致 k（L）的降低。另外，相對穩定的電弧使得Uarc（L）和 k（L）的波動劇烈程度下降，說明模型參數對于冶煉時期以及弧長變化的追蹤性能良好。

電弧爐的動態特性如圖6所示，對比圖4可以看出，精煉期電弧電流和電壓的波形變得平穩，由于弧長降低，燃弧電壓和熄弧電壓的幅值也大幅下降，電弧電流增大。特別地，在電弧電流過零點處，由于燃弧電壓降低，伏安特性曲線的軌跡由尖銳變得平緩；電弧電流增大，非線性減弱，“零休”現象不如熔化期顯著，導致伏安特性曲線的傾斜度降低。同樣地，35kV母線A相電壓曲線如圖7所示，其最大電壓波動值為1.17%，未超出國標限值。

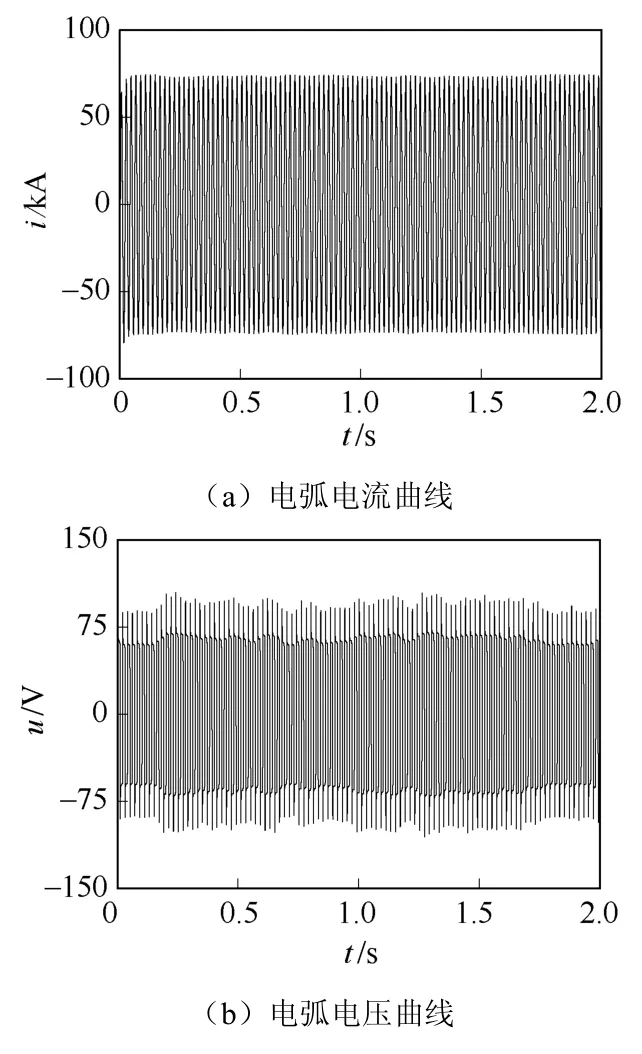
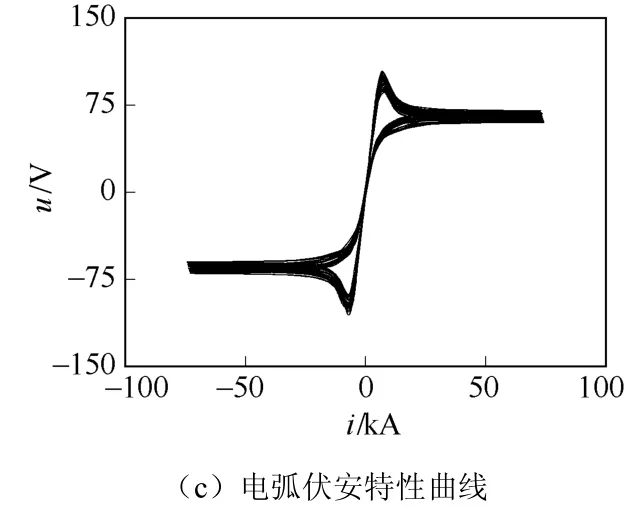
圖6　精煉期電弧爐的動態特性

圖7　精煉期35kV母線A相電壓曲線

通過表2可以觀察到，精煉期的諧波電流較熔化期大幅下降，特別是5次和7次諧波，已降至國標允許值以下，電弧爐在精煉期對電網的污染較小，仿真結果與實際相吻合。

3　結論

本文提出了一種基于能量守恒定律，以電弧導納為狀態變量，電弧電流和弧長作為輸入的交流電弧爐模型，創新地采用隨弧長連續隨機變化的模型參數Uarc（L）和k（L），并給出了相應的工程估算方法，兩者均與弧長相關，有明確的物理意義。分別對熔化期和精煉期的電弧爐特性以及電網電壓波動和諧波進行了仿真分析，仿真結果與實測數據對比表明，該模型能夠準確地模擬不同冶煉時期電弧爐的動態特性以及造成的電網電壓波動和諧波污染。

本文提出的時變參數模型區別于以往的從能量平衡關系出發或基于實測數據建立的模型。一是可以通過時刻變化的參數精確地模擬電弧爐在不同運行階段的動態特性，避免了采用固定參數來仿真時變系統的不足；二是只需電弧爐系統的初始設計參數就可以實現模型的仿真，從而并不僅僅針對特定的電弧爐，因此具有準確性和普適性。該模型適用于預測和評估電弧爐接入電網后可能引發的電能質量問題，以便提前采取相應的治理措施，具有一定的工程應用價值。

［1］ 彭卉，鄒舒，付永生，等. 沖擊負荷接入電網的電能質量分析與治理方案研究［J］. 電力系統保護與控制，2014，42（1）︰54-61.

［2］ 金維剛，劉會金，李智敏，等. 3種典型間諧波源的間諧波測量及結果分析［J］. 電力自動化設備，2010，30（12）︰30-35.

［3］ 劉書銘，李瓊林，陳棟新，等. 中高壓配電網非線性用戶的電能質量特性研究［J］. 電力系統保護與控制，2012，40（15）︰150-155.

［4］ 鞠平，王耀，項麗，等. 考慮特殊負荷的寧夏電網負荷建模［J］. 電力自動化設備，2012，32（8）︰1-4，21.

［5］ 王育飛，姜建國. 用于電能質量研究的新型交流電弧爐混沌模型［J］. 中國電機工程學報，2008，28（10）︰106-110.

［6］ Alonso M P，Donsion M P. An improved time domain arc furnace model for harmonic analysis［J］. IEEE Transactions on Power Delivery，2004，19（1）︰367-373.

［7］ Montanari G C，Loggini M，Cavallini A，et al. ARC-FURNACE MODEL FOR THE STUDY OF FLICKER COMPENSATION IN ELECTRICAL NETWORKS［J］. IEEE Transactions on Power Delivery，1994，9（4）︰2026-2036.

［8］ Acha E，Semlyen A，Rajakovic N. A HARMONIC DOMAIN COMPUTATIONAL PACKAGE FOR NONLINEAR PROBLEMS AND ITS APPLICATION TO ELECTRIC-ARCS［J］. IEEE Transactions on Power Delivery，1990，5（3）︰1390-1397.

［9］ 池偉，張愷倫，查蕾，等. 基于能量平衡的電弧爐模型的仿真與參數辨識［J］. 機電工程，2012，29（4）︰454-457.

［10］ 王晶，束洪春，林敏，等. 用于動態電能質量分析的交流電弧爐的建模與仿真［J］. 電工技術學報，2003，18（3）︰53-58.

［11］ Wang Yan，Mao Zhizhong，Tian Huixin，et al. Modeling of electrode system for three-phase electric arc furnace［J］. Journal of Central South University of Technology，2010，17（3）︰560-565.

［12］ 劉小河，趙剛，于娟娟. 電弧爐非線性特性對供電網影響的仿真研究［J］. 中國電機工程學報，2004，24（6）︰30-34.

［13］ 陳大宣，余一平，鞠平，等. 基于時變電流注入方法的特殊電力負荷建模研究［J］. 電力自動化設備，2014，34（3）︰120-124.

［14］ Chang Gw，Min-Fu S，Chen Yiying，et al. A hybrid wavelet transform and neural-network-based approach for modelling dynamic voltage-current characteristics of electric arc furnace［J］. IEEE Transactions on Power Delivery，2014，29（2）︰815-824.

［15］ 王其平. 電器電弧理論［M］. 北京︰機械工業出版社，1982.

［16］ 王豐華. 電弧爐建模研究及其應用［D］. 上海︰上海交通大學，2006.

［17］ Paschkis，Persson. Industrial electric furnaces and appliances［M］. new york︰interscience publishers，1960.

［18］ （日） 南條敏夫，李中祥. 煉鋼電弧爐設備與高效益運行［M］. 北京︰冶金工業出版社，2000.

［19］ Manchur G，Erven CC. Development of a model for predicting flicker from electric arc furnaces［J］. IEEE Transactions on Power Delivery，1992，7（1）︰416-426.

［20］ 仝永博，劉征，羅玉鐲，等. 采用長弧操作的高阻抗電弧爐［J］. 冶金設備，2014（6）︰20-24.

Time-varying Parameter Model of AC Electrical Arc Furnace for Power Quality Predictions and Analysis

Liao Yantao1Hu Jun1Zhang Hailong2Wang Enrong1
（1. College of Electrical and Automation Engineering，Nanjing Normal University，Nanjing210042；2. College of Physics and Technology，Nanjing Normal University，Nanjing210023）

A novel time domain differential model is proposed for the AC EAF （Electrical Arc Furnace） based on the law of conservation of energy. The model is established with arc admittance as a state variable，and with arc current and arc length as the input. The relation between the parameters with arc length is derived from the formula of the arc length and voltage. The engineering estimation method of time-varying parameters are further realized. Moreover，the limited bandwidth random signal is added on the arc length，and actual working state was simulated. A real EAF is taken to simulate the dynamic characteristics as well as the grid voltage fluctuation and harmonic wave in melting and refining stages. The results coincide with the measured data so prove the validity and practicability of the model.

electrical arc furnace；arc impedance；time-varying parameter；power quality；load modeling

廖延濤（1990-），男，安徽淮南人，碩士研究生，主要從事電力系統沖擊負荷電能質量分析與治理。

國家自然科學基金項目（51475246）

江蘇省普通高校研究生科研創新計劃項目（KYLX15_0725）