超微晶合金旋轉磁特性測量用勵磁裝置的設計與優化

陳 龍 汪友華 趙浛宇 戈文祺 王 苗

?

超微晶合金旋轉磁特性測量用勵磁裝置的設計與優化

陳 龍 汪友華 趙浛宇 戈文祺 王 苗

（河北工業大學電磁場與電器可靠性省部共建重點實驗室 天津 300130）

旋轉磁心損耗廣泛存在于高頻變壓器T形連接點處與高速電機的定子上。為了對二者進行更好的分析，需要將高頻下的旋轉磁心損耗進行精確測量。本文就四種不同的勵磁結構進行有限元分析，闡述了勵磁結構對準確度的影響。在此基礎上，根據超微晶物理特性提出一種立體式二維高頻勵磁裝置，對勵磁繞組進行計算，并優化設計了磁軛結構，將測試頻率提高到10kHz。

超微晶合金 二維旋轉磁特性 高頻勵磁裝置 優化設計

0 引言

高速電機與高頻電工設備由于其較高的功率密度，而具有廣泛的應用前景[1-4]。超微晶合金與非晶合金等新興材料被廣泛應用于各種高頻領域[5]。但是，目前僅限于一維超微晶磁特性的測量[6]。日本學者測試了二維非晶合金，但頻率最高只達到750Hz[7]。為了在電機設計過程中更有效地分析材料在高頻下的損耗，有必要對超微晶合金的高頻旋轉磁特性進行精確測量。

當頻率達到1kHz以上時，二維磁化問題變得十分復雜，相比一維，其對勵磁電源提出了更高要求。在保證樣片磁化均勻的前提下，選擇合適的勵磁結構顯得尤為重要。

目前世界上對二維旋轉磁化問題的研究已有三十多年[8]，早期的旋轉磁特性主要是通過測量樣片在旋轉過程中受到的轉矩，計算其旋轉一周的平均損耗[6]。但這種方法校準十分困難，很難分離出在旋轉過程中因摩擦力等因素帶來的誤差。自1965年起，有學者開始研究用溫度傳感法測量旋轉磁心損耗，其表達式為

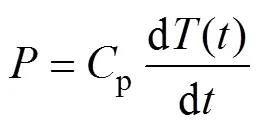
式中，p、()分別為被測樣片的比熱和溫度。該方法在磁通密度較高時有較好的準確度和靈敏度，但磁通密度較低時靈敏性較差，并且對樣片絕熱十分困難，因此，限制了該方法的廣泛應用。磁場計算測量法由于實施簡單、準確度高、可重復性好，得到了國際上的廣泛認可。在磁場計算測量法中，通過樣片磁化后測得的磁場強度和磁通密度可得到磁心損耗，由坡印亭定理經過一系列推導可得旋轉磁心比損耗t為

（2）

為了在樣片中模擬變壓器T形連接點與電機齒部所產生的旋轉磁場，德國、意大利、奧地利和日本學者分別建立了不同的勵磁裝置[9-14]。這些裝置大體上可按樣片形狀分為三類：基于方形樣片的十字形單片測量儀（Square Rotational Single Sheet Tester, SRSST）、基于六邊形樣片的單片測量儀（Hexagonal Rotational Single Sheet Tester, HRSST）和基于圓形樣片的類感應電機式單片測量儀（Round Rotational Single Sheet Tester, RRSST）。但這些裝置都只適合低頻情況下的勵磁（幾百Hz）。為了測試更高頻率，意大利國家計量學院研制了基于三相勵磁的二維高頻勵磁裝置（3 Phase-RRSST, 3P-RRSST）[15]，其是在原類電機勵磁結構的基礎上進行了改進，采用集中繞組，減小了每相繞組的磁通，從而將測試頻率提高到5kHz。然而國際上還沒有形成統一的二維磁特性測量標準，其中一部分原因是二維磁特性測量的可重復性較差，各種測量裝置測量結果有一定偏差[16]。

本文分別建立上述四種主要勵磁裝置的有限元模型，以15°為步長分析了樣片的磁化性能。首先，對比了不同裝置磁化對樣片均勻性的影響；其次，分析了不同結構的勵磁性能；最后，根據分析結論，考慮超微晶合金本身的物理特性[17]，提出一種適合超微晶二維高頻磁特性測量的立體式勵磁裝置。

1 勵磁結構對樣片磁化均勻性的影響

樣片形狀與其對應的勵磁結構對樣片磁化的均勻性有重要影響。四種不同的勵磁結構如圖1所示。SRSST結構最早由W. Brix提出[18]，之后有很多改進版本[19-24]。其主要原理是在空間相對正交的兩個磁極上纏繞繞組，通有相位正交的兩相電流，在樣片中產生旋轉磁場。HRSST由H. Pfützner于1996年提出[25]，由于該結構采用多對磁極的三相勵磁系統，使矢量的軌跡更接近圓形。RRSST將傳統感應電機的轉子替換為圓形樣片，如圖1c所示，在定子中纏繞正交分布的兩相分布式繞組，在較低磁通密度下無反饋控制也可以達到圓形旋轉磁場。3P- RRSST[26]結構如圖1d所示，此結構由于是三相勵磁，在波形上更容易實現圓形控制。

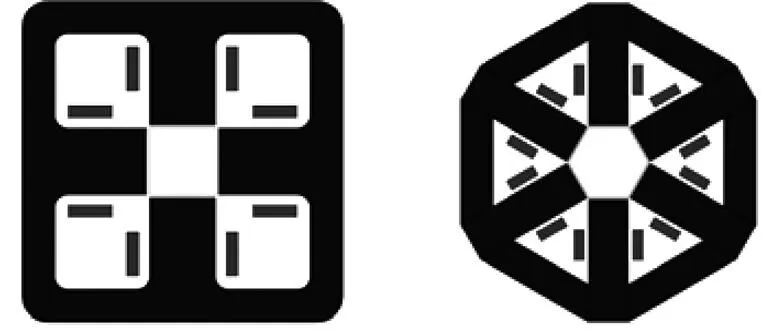
（a）SRSST???（b）HRSST

（c）RRSST???（d）3P-RRSS

圖1 四種不同的勵磁結構

Fig.1 Four different structure of magnetizer

測量過程中，樣片中央位置分別在方向和方向上垂直放置兩組H線圈與B線圈。從而用一定區域內磁場的均值來模擬中心點處磁場的大小和方向。磁場矢量計算式為

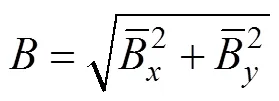
（4）

為了得到更精確的結果，樣片磁化的均勻性對測量結果起著重要的影響。氣隙作為樣片磁化中非常關鍵的參數，對磁化的均勻度影響很大。這主要是由于不同氣隙條件下樣片中退磁場分布不均，而退磁場隨氣隙的減小而減小。考慮到實際加工的準確度，這個值并不能無限減小。而文獻[27]未提及氣隙的影響，為了說明勵磁結構對樣片均勻性的單一影響，本文所分析的四種結構使用統一的參數：氣隙大小=0.5mm，樣片內切圓直徑。

計算過程中，不考慮樣片材料的各向異性，認為樣片在不同方向上具有相同的磁化曲線。為了得到更精確的結果，樣片部分網格剖分采用極端細化網格，樣片被磁化到1T左右。當磁化角度為45°時，四種結構中樣片的磁力線分布與磁通密度分布分別如圖2和圖3所示。

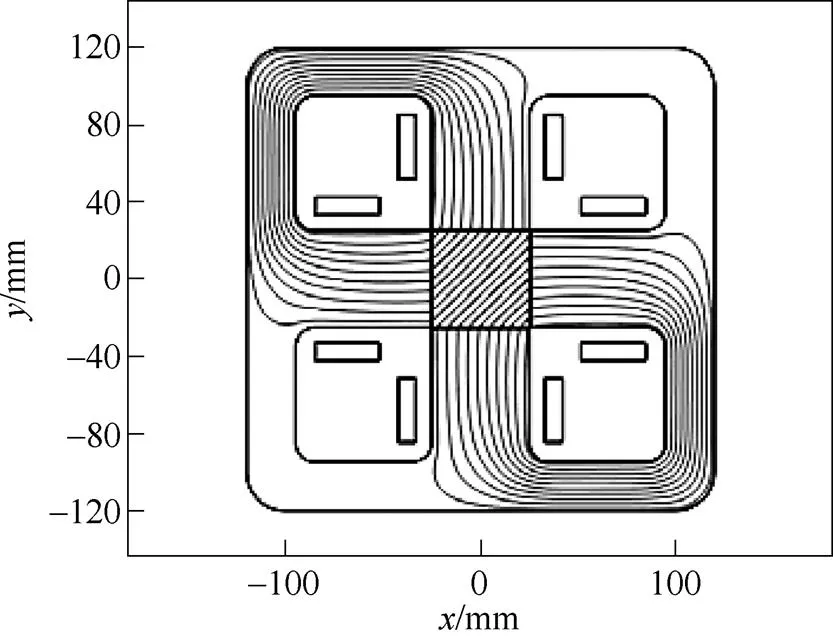
（a）SRSST

（b）HRSST

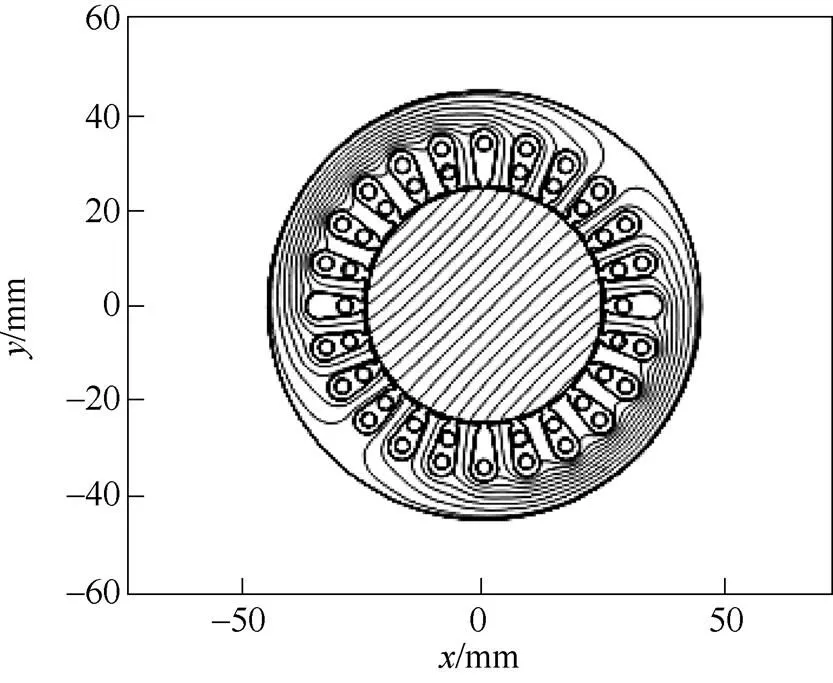
（c）RRSST

（d）3P-RRSST

圖2 不同勵磁裝置的磁力線分布

Fig.2 Flux lines distribution of differnet magnetizers

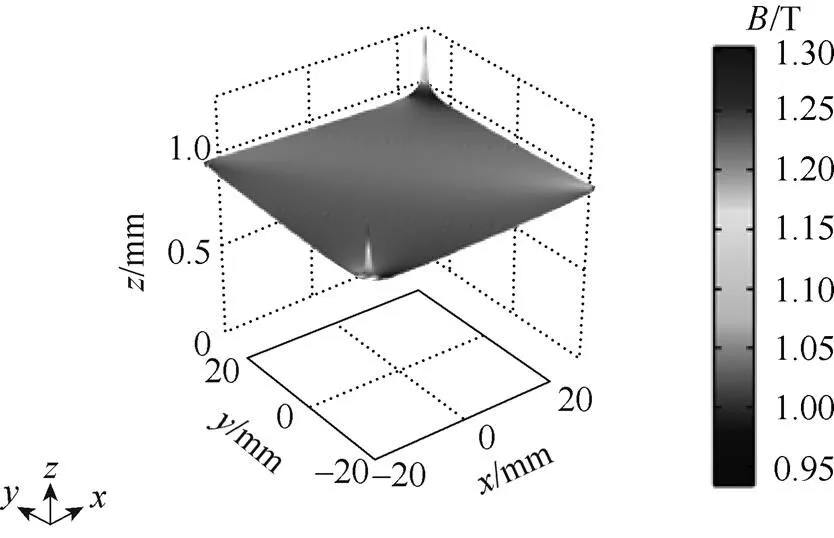
（a）SRSST

（b）HRSST

（c）RRSST

（d）3P-RRSST

圖3 不同勵磁裝置的磁通密度分布

Fig.3 Magnetic flux density distribution of different magnetizers

由圖2和圖3可知，方形樣片和六邊形樣片所對應的勵磁結構在頂角處磁通密度較高，但樣片整體磁通密度分布比較均勻。而圓形樣片對應的勵磁結構，由于存在齒槽效應，樣片邊緣的磁通密度變化劇烈，縮小了樣片的可測量范圍，對于兩相感應電機式勵磁裝置，存在明顯的弱磁區，磁力線在對應磁化角度45°與135°的區域向兩邊分散，導致這部分的磁通密度較低。而對三相勵磁結構各相磁通進行了補償，沒有出現明顯的弱磁區，但是齒槽磁阻周期性變化劇烈，導致了磁通密度隨圓周振蕩劇烈。在方形樣片與六邊形樣片的勵磁裝置中，由于微小氣隙的存在（=0.5mm），減小了磁極間的相互吸引，使磁力線大部分從樣片中經過，減小了漏磁，因此導致樣片的磁通密度分布相對均勻。

為了進一步定量分析樣片的均勻性，將樣片上各點磁通密度標準差作為定量分析樣片均勻性的標準，其計算式為

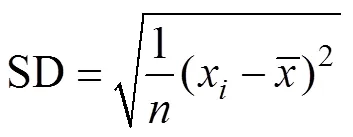
式中，x為樣片區域內每個點的磁通密度大小；為整個樣片磁通密度的均值。

圖4和圖5分別給出了半個周期內樣片磁通密度分布的標準差與均值隨著角度變化的分布。如圖4所示，在相同氣隙條件下，四種結構中方形樣片所對應的SRSST具有最小的標準差，磁通密度分布在整個樣片的變化最小，六邊形樣片次之。這與圖3磁通密度三維云圖的結果是吻合的。圓形樣片所對應的RRSST與3P-RRSST的標準差較高，反映出弱磁區與齒槽效應對樣片均勻性的影響。方形樣片與六邊形樣片在不同磁化角度上的標準差出現不同程度的振蕩，而圓形樣片在不同角度上變化很小，說明圓形樣片在不同磁化角度上的磁化狀態是一致的。圖5進一步驗證了上述觀點。圓形樣片在一個磁化周期內樣片內的磁通密度基本保持不變，而方形樣片和六邊形樣片由于磁路不對稱，在不同角度上表現出不同的磁化能力。對于方形樣片SRSST在45°、135°等方向上，在氣隙中磁力線長度大于0°、90°與180°的情況，相對磁阻較大，從而在相同的磁動勢下這些角度上的磁通密度相對較低。類似的結論也可以從六邊形樣片的勵磁結構中得到。而圓形樣片由于磁路對稱，在不同磁化角度上磁阻處處相等，磁通密度大小保持恒定，可以實現標準圓形磁化。

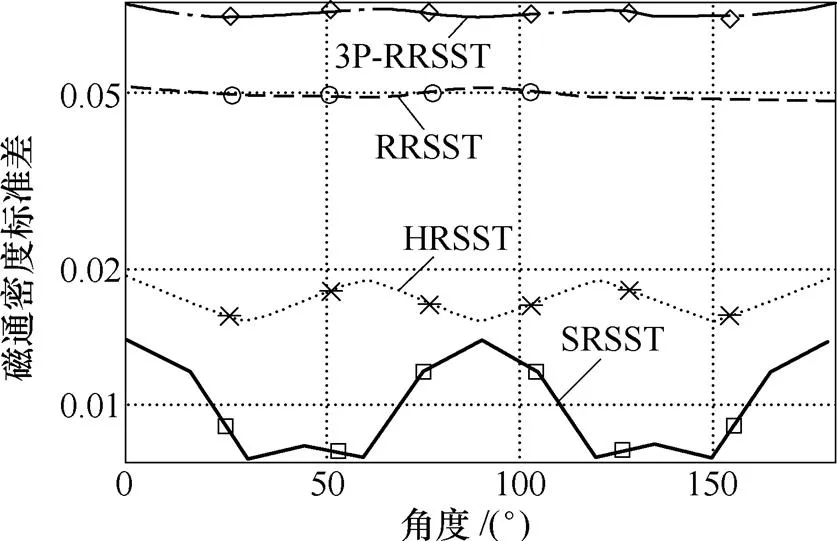
圖4 磁通密度標準差隨磁化角度的分布

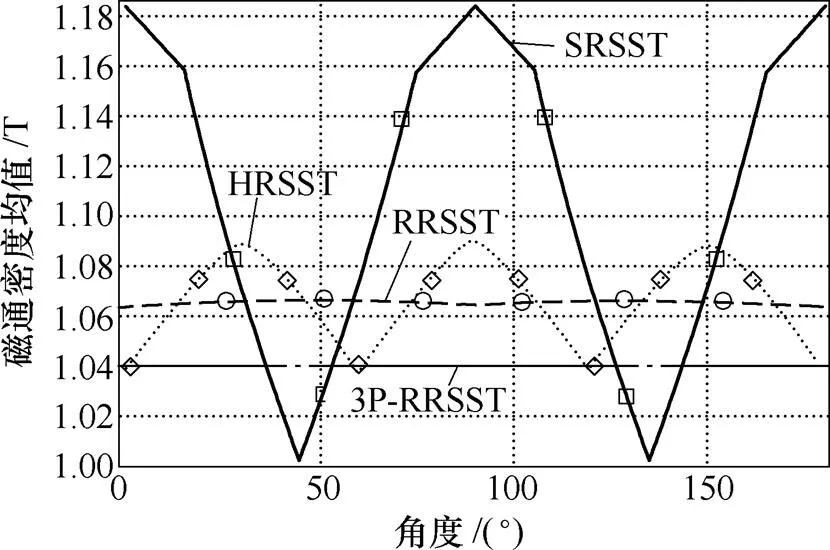
圖5 磁通密度均值隨磁化角度的分布

由上面分析可知，在不考慮材料各向異性的情況下，從樣片均勻度的角度考慮，方形樣片具有更低的磁通密度變化；從實現圓形控制角度考慮，圓形樣片更容易達到開環的圓形旋轉磁場，而降低了對控制程序的要求。但是超微晶合金材料不是完全的各向同性，所以無論哪種結構都需要反饋的調節。對于方形樣片和六邊形樣片，在實際測量過程中需要更強的反饋算法才能保證圓形旋轉磁場的實現。通過考察整體的標準差和圖3的磁通密度云圖，可為傳感器的設計提供理論指導，從而進一步提高高頻磁場測量的傳感器靈敏度。

2 超微晶磁心勵磁結構設計

由勵磁結構對樣片磁化均勻性的分析可知，當樣片被磁化到1T時，基于方形樣片的SRSST在一個周期內的各個角度上均具有最好的均勻性。超微晶磁心的飽和磁通密度在1.23T左右，完全滿足測量需求。考慮到超微晶帶材寬度一般為50mm且易碎，圓形樣片的加工成本遠超過方形樣片。在均勻度滿足要求的前提下，綜合考慮，本文設計了基于方形樣片的超微晶高頻旋轉測量裝置。由于超微晶合金通常應用在高頻領域，而傳統的SRSST只能工作在幾百Hz的頻率下，所以需要在傳統的勵磁結構上進行改進。本文提出的超微晶高頻旋轉勵磁裝置如圖6所示，可將測試頻率提高到10kHz。

（a）模型?????（b）實物

2.1 勵磁結構的磁路設計

當頻率達到1kHz以上時，磁心的發熱問題及磁場的建立都變得十分困難。若用傳統的硅鋼疊制成磁心，在10kHz時磁心發熱十分嚴重，容易破壞繞組絕緣，引起安全問題。超微晶帶材擁有超高的磁導率及在高頻下接近硅鋼1/10的損耗[28]，非常適合在頻率1～20kHz的頻段內工作。所以本文以超微晶材料作為制作磁心的帶材。對于傳統的平面式SRSST[29]，采用四個磁極與四個L形磁軛構成閉合磁路，在磁極與L形磁軛連接處，磁通垂直傳入帶材表面，引起較大渦流損耗，并且絕緣介質增大了磁動勢降落，導致需要更大的電流才能將樣片磁化到飽和，這樣提高了對電源的要求。本文提出的雙C形立體式勵磁結構有效地避免了這一問題，并且兩條相互垂直的磁路相互獨立，可以分開計算。若忽略漏磁場，由安培環路定律得

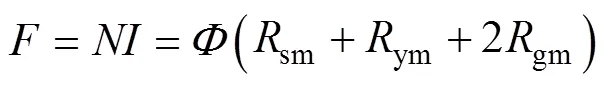
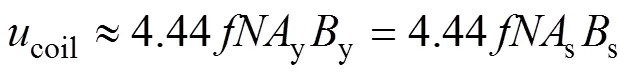
式中，y、s分別為磁心截面積與樣片截面積；ys分別為磁心磁通密度與樣片磁通密度。實際情況下，由于漏磁通的存在，樣片磁通并不完全等于磁心磁通。由于被測樣片極薄，空氣中的漏磁通a可由不放樣片時測得，從而計算得到考慮漏磁場下的修正系數a，則式（7）可修正為

（8）

由式（6）可知，為了避免磁心過熱，應降低磁心磁通密度y，因而磁心應保證一定的厚度。

2.2 幾何結構的優化

本文為了減小高頻的電容效應，將繞組分別纏繞在了兩只磁心的磁軛上，而這樣會增加磁極雜散磁場的分布，這部分磁場會縮小樣片均勻區域的大小，影響樣片的均勻性。磁屏蔽層對樣片均勻性的影響如圖7a和圖7b所示。由圖7可見，在沒有屏蔽層的情況下，通過三維有限元計算可發現，磁極中的一部分磁通在空氣中與另一邊磁極閉合，導致在樣片邊緣處的磁場要小于中心部位。而增加了屏蔽層后，外部磁場在屏蔽層處閉合，屏蔽層內部沒有雜散磁場，樣片的均勻區域幾乎擴大到整個樣片。此外，在高頻測量時，如何有效去除與測量頻率接近的空間諧波是一大難題。由于屏蔽層的存在，屏蔽層內部空間可避免外界磁場的干擾，這對高頻測量十分重要，可有效分離出有效信號，提高測量準確度。

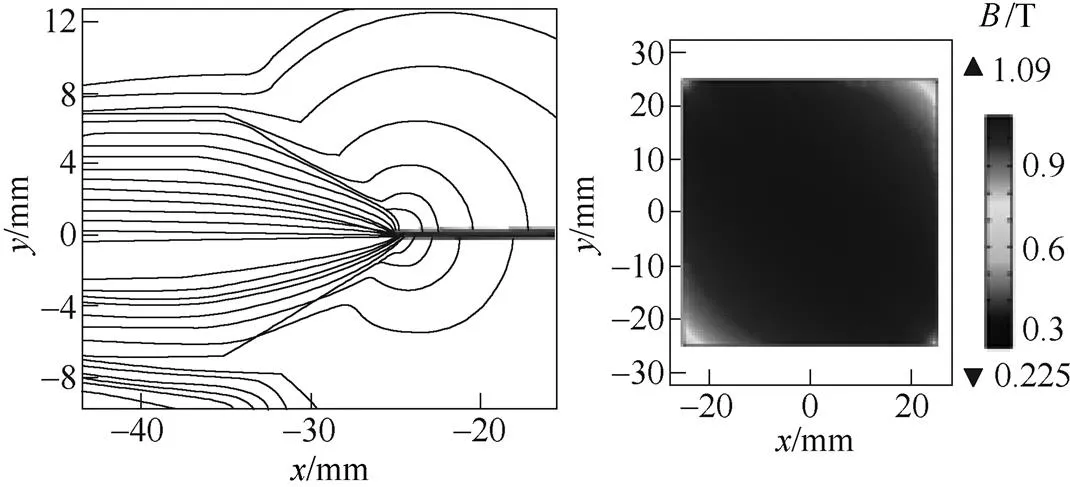
（a）磁力線分布（未加屏蔽層）?（b）磁通密度分布（未加屏蔽層）

（c）磁力線分布（加屏蔽層）?（d）磁通密度分布（加屏蔽層）

圖7 磁屏蔽層對樣片均勻性的影響

Fig.7 Influence of the magnetic shielding on sample uniformity

在考慮屏蔽層后，屏蔽層與樣片的距離、磁極間各部分的尺寸也顯得尤為重要。文獻[30,31]分析了當磁極形狀為楔形時，具有較好的聚磁效果；當楔角為54.5°時，中心獲得最大磁場。但實際氣隙存在樣片時，磁路接近閉合磁路的情況，樣片的存在將影響周圍空間磁場的分布，最優的楔角還需要進一步修正。由于在考慮樣片時，不能得到精確的解析表達式，本文以當樣片被磁化到1T時所需的功率為優化目標，以自適應模擬退火法[32]作為優化算法，對這一問題進行了優化。磁極尺寸的設計參數如圖8所示。

圖8 磁極尺寸的設計參數

圖8中，1為磁心磁軛厚度，2為磁極高度，3為磁極長度，4為屏蔽層到樣片的距離。氣隙大小沒有作為優化設計的變量，氣隙越小，所需磁動勢越小，樣片均勻性的退磁磁場越小。由于機械加工準確度的原因，本文設計的超微晶磁心樣片與磁極的距離設定為0.3mm。由于=[1234]這一組變量，并不是相互獨立的，所以不能通過參數化掃描的方式來確定最終的尺寸，需要進行全局優化。本文通過Comsol與Matlab聯合仿真，在Matlab中編寫優化算法，實現了對參數的優化。優化問題可總結為

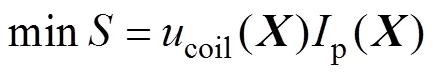
（11）

式中，coil()、p()分別為當樣片磁通密度為1T時繞組的電壓和電流，可通過對磁心有限元模型進行頻域分析得到；為設計變量，=[1,2,3,4]，下限min為幾何尺寸的約束，min[2, 0.2, 0.2, 0.2]，上限max[25, 25, 25, 5]。考慮楔角的極限情況，為保證磁極的楔形，有

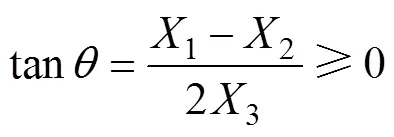
（1）初始化。設定可行域，最大溫度max，下降速率，步長，初始min及每一代的個體數rp。

（2）在T溫度下，按一定規律隨機產生一個步長，生成rp個個體，通過有限元計算，計算每個個體的目標函數值S。

（3）每個S與min作比較，若S≤min則接受，并更新min；若S＞min則按式（13）進行判斷。

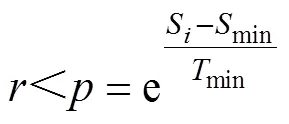
式中，為[0,1]上的偽隨機數；為玻耳茲曼概率。在整個過程中，統計T下S＞min的次數1與被接受的次數2。

（4）降低溫度T并回到步驟（2）迭代。若2/1偏大，則優化過程中限制了下山性，加大下降速率；若2/1偏小，則限制了上山性，此時T下降速率應比原來小一些。

這樣，經過反復迭代，得到磁極初始與優化后的尺寸見表1。由表1可看出，最終的優化尺寸對電源功率的需求降低了36%，提高了高頻勵磁裝置的勵磁能力。

表1 磁極初始與優化后的尺寸

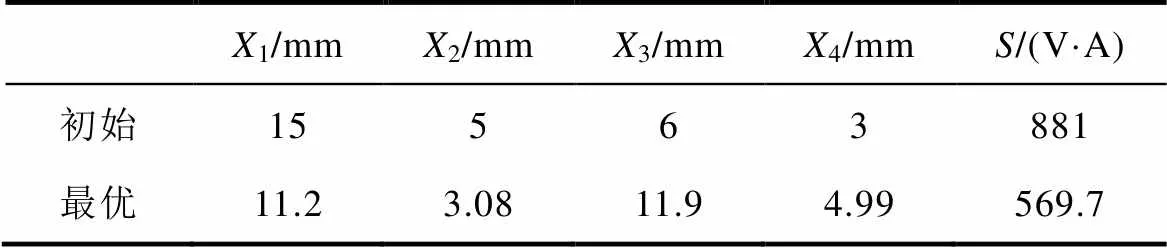
Tab.1 Initial and optimal size of the magnetic pole

2.3 勵磁繞組的設計

當頻率升高時，導體之間的電容效應、趨膚效應和鄰近效應不能忽略。為減小高頻時兩相繞組的電容效應，將單層繞組纏繞在磁心的軛部上，由于磁心厚度遠大于樣片厚度，即使樣片飽和，磁心磁通密度仍然較低，具有較高的磁導率，因此漏磁較小，可忽略不計。為了減小高頻時繞組的趨膚效應與鄰近效應帶來的損耗，用litz線制作了單層繞組，litz線單根導體半徑為

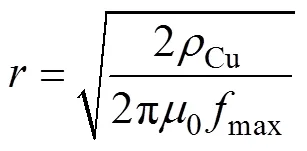
式中，Cu為銅的電阻率；0為真空磁導率；max為最高實驗頻率。由于litz線采用ETFE絕緣，極限溫升可達155℃，最大電流密度為5A/mm2，因此，繞組最大電流為

（15）

式中，Cu為單根導線截面積；max為導體能承受的最大電流密度。最終匝數為

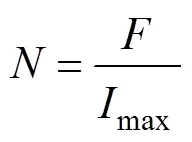
式中，為磁動勢。通過三維有限元計算可得到，當樣片被磁化到1T時，litz線電流為8.9A，對應繞組的匝數為12匝、繞組長度為37.5mm。最終繞組的電感可由計算磁場能量得到，直流電阻由LCR分析儀測得為0.061W。為減小高頻的損耗，本文采用的litz繞組線徑為0.01mm，分5股，每股60匝，共300根漆包線。在10kHz時，交流電阻為直流電阻的5倍，相較電抗的變化，整體阻抗主要由電抗決定。為了減小電抗以適應更高頻率的測試，須減小最終設計的勵磁電感。本文設計的litz繞組實際上是增大了單位通流能力，從而在保證安匝數不變的情況下，減小了匝數，進而減小了勵磁電感。勵磁繞組電壓為

（17）

式中，ac為繞組等效交流電阻；為繞組等效電感；為繞組電流。

當頻率為10kHz時，繞組上的勵磁電壓為65.52V，對應電感為0.116mH，由此得到視在功率=589V·A。為了將樣片磁化到更接近飽和，在10kHz條件下，兩相繞組分別加載10A電流，可由實驗室購買的功放AE 7548安全提供。

3 實驗裝置的可行性

高頻旋轉勵磁裝置的勵磁實驗系統如圖9所示，主要包括以下幾部分：美國NI公司提供的PXI測試平臺，通過高性能的多功能DAQ卡實現信號的產生并采集；兩臺高性能的線性功放，可以實現DC～50kHz的功率放大，為超微晶高頻勵磁裝置提供勵磁電流；超微晶二維高頻勵磁裝置及復合式B&H傳感器。當磁通密度較小時，傳感器產生的信號較小，且周圍空間中存在一些干擾磁場。對傳感器信號的前置處理如圖10所示，本課題組通過SR560得到了較好的結果。圖11給出了當p=1.0T、= 10kHz時兩相繞組上的電壓和電流波形，可看出電流波形基本符合計算結果，而電壓略高于計算值，這主要是因為litz線在高頻時交流電阻的上升，但并不影響整體實驗。

（a）實驗框圖

（b）實物圖

圖9 高頻旋轉勵磁裝置的勵磁實驗系統

Fig.9 Exciting experiment system of the high frequency rotational magnetizer

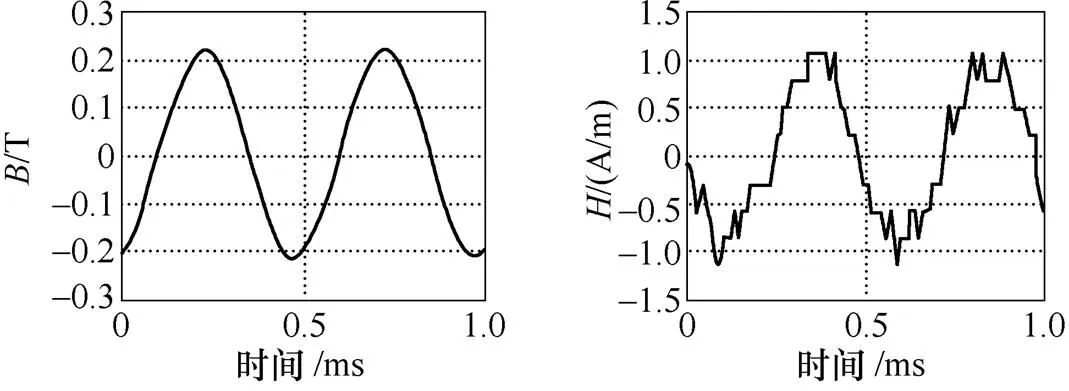
（a）處理前

（b）處理后

圖10 對傳感器信號的前置處理

Fig.10 Preprocessing of the sensor signal

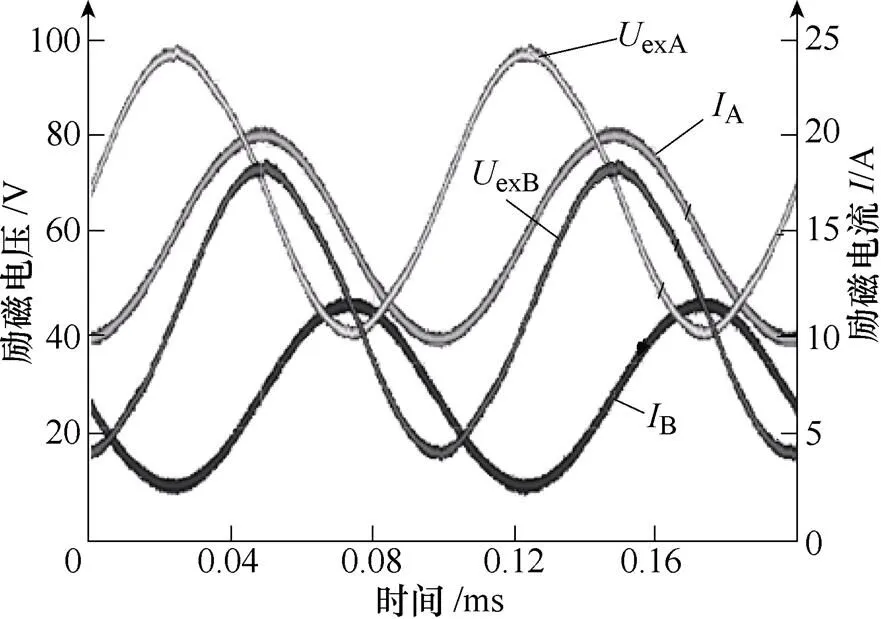
圖11 兩相繞組上的電壓和電流波形

4 結論

本文對四種主要的二維磁特性測量裝置進行了有限元分析。通過比較，發現方形樣片及其所對應的勵磁結構在不同磁化角度上都具有最好的均勻性，但是不同方向的磁化能力不同，產生圓形旋轉磁場時需要結合適當的反饋算法。而圓形樣片對應的勵磁結構由于齒槽效應，影響了樣片的均勻性。基于分析比較，本文以方形樣片為基礎，提出了一種立體式高頻旋轉勵磁裝置，針對高頻繞組電容效應、趨膚效應對繞組進行了改進，然后分析了磁極雜散磁場對樣片均勻性的影響，提出了添加屏蔽層的方案，使樣片均勻的區域幾乎擴大到整個樣片，提高了測量的準確性。最后，在考慮磁屏蔽層的情況下，對磁極尺寸進行了優化，采用優化后的勵磁裝置，勵磁效果提高了36%，明顯降低了對電源的要求，采用超微晶磁心的勵磁裝置可以將測量頻率擴展到10kHz。

參考文獻：

[1] 趙爭菡, 汪友華, 凌躍勝, 等. 大容量高頻變壓器繞組損耗的計算與分析[J]. 電工技術學報, 2014, 29(5): 261-264, 270.

Zhao Zhenghan, Wang Youhua, Ling Yuesheng, et al. Calculation and analysis of loss in high-capacity high-frequency transformers[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 261-264, 270.

[2] 張樹東, 朱大為, 劉闖, 等. 交直流混合配電型通用功率變換器（UPC）研究[J]. 電力系統保護與控制, 2016, 44(1): 48-55.

Zhang Shudong, Zhu Dawei, Liu Chuang, et al. Universal power converter (UPC) for hybrid AC and DC distribution[J]. Power System Protection and Control, 2016, 44(1): 48-55.

[3] 王曉毛, 梅桂華, 謝應耿. 基于高頻開關電源的反向注入式直流平衡裝置的研究及應用[J]. 電力系統保護與控制, 2015, 43(8): 139-144.

Wang Xiaomao, Mei Guihua, Xie Yinggeng. Research and application of reverse injection DC- balancing device based on high-frequency switching power supply[J]. Power System Protection and Control, 2015, 43(8): 139-144.

[4] 丁茂生, 王輝, 舒兵成, 等. 含風電場的多直流送出電網電磁暫態仿真建模[J]. 電力系統保護與控制, 2015, 43(23): 63-70.

Ding Maosheng, Wang Hui, Shu Bingcheng, et al. Electromagnetic transient simulation model of multi-send HVDC system with wind plants[J]. Power System Protection and Control, 2015, 43(23): 64-70.

[5] Shen W, Ferd W, Boroyevich D, et al. High-density nanocrystalline core transformer for high-power high-frequency resonant converter[J]. IEEE Transa- ctions on Industry Applications, 2008, 44(1): 213-222.

[6] Sergeant P, Dupre L. Modeling the electromagnetic behavior of nanocrystalline soft materials[J]. IEEE Transactions on Magnetics, 2009, 45(2): 678-686.

[7] Ueno S, Todaka T, Enokizono M. Measurement of vector magnetic properties of Fe-Si-B amorphous material[J]. IEEE Transactions on Magnetics, 2011, 47(10): 3188-3191.

[8] 李丹丹, 劉福貴, 李永建, 等. 一種新的混合矢量磁滯模型磁滯算子定義方法[J]. 電工技術學報, 2015, 30(1): 15-21.

Li Dandan, Liu Fugui, Li Yongjian, et al. A new definition of the hysteron in hybrid vector hysteresis model[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 15-21.

[9] Guo Y G, Zhu J G, Zhong J J, et al. Measurement and modeling of rotational core losses of soft magnetic materials used in electrical machines: a review[J]. IEEE Transactions on Magnetics, 2008, 44(2): 279-291.

[10] Pfutzner H. Rotational magnetization and rotational losses of grain oriented silicon steel sheets- fundamental aspects and theory[J]. IEEE Transa- ctions on Magnetics, 1994, 30(5): 2802-2807.

[11] Pfutzner H, Mulasalihovic E, Yamaguchi H, et al. Rotational magnetization in transformer cores—a review[J]. IEEE Transactions on Magnetics, 2011, 47(11): 4523-4533.

[12] Takahashi N, Mori Y, Yunoki Y, et al. Development of the 2-D single-sheet tester using diagonal exciting coil and the measurement of magnetic properties of grain-oriented electrical steel sheet[J]. IEEE Transa- ctions on Magnetics, 2011, 47(10): 4348-4351.

[13] Maeda Y, Shimoji H, Todaka T, et al. Rotational power loss of magnetic steel sheets in a circular rotational magnetic field in CCW/CW directions[J]. Journal of Magnetism and Magnetic Materials, 2008, 320(20): 567-570.

[14] Ragusa C, Zurek S, Appino C, et al. An inter- comparison of rotational loss measurements in non-oriented Fe-Si alloys[J]. Journal of Magnetism and Magnetic Materials, 2008, 320(20): 623-626.

[15] De la Barriere O, Appino C, Fiorillo F, et al. A novel magnetizer for 2D broadband characterization of steel sheets and soft magnetic composites[J]. International Journal of Applied Electromagnetics and Mechanics, 2015, 48(2-3): 239-245.

[16] Sievert J, Ahlers H, Birkfeld M, et al. European intercomparison of measurements of rotational power loss in electrical sheet steel[J]. Journal of Magnetism and Magnetic Materials, 1996, 160(7): 115-118.

[17] Swieboda C. Current and future use of the nanocry- stal line strips[C]//3rd International Students Conference on Electrodynamics and Mechatronics, 2011: 151-154.

[18] Brix W, Hempel K, Schulte F. Improved method for the investigation of the rotational magnetization process in electrical steel sheets[J]. IEEE Transa- ctions on Magnetics, 1984, 20(5): 1708-1710.

[19] Enokizono M, Shirakawa G, Suzuki T, et al. Two- dimensional magnetic properties of silicon-steel sheet[J]. IEEE Translation Journal on Magnetics in Japan, 1991, 6(11): 937-946.

[20] Zhang Y L, Chu X, Young H E, et al. An improved magnetic property modeling for electrical steel sheets based on double-exciting type 2D measuring system[C]// International Conference on Electrical Machines and Systems, Wuhan, 2008: 4053-4056.

[21] Zhu J G, Zhong J J, Ramsden V, et al. Power losses of soft magnetic composite materials under two- dimensional excitation[J]. Journal of Applied Physics, 1999, 85(8): 4403-4405.

[22] Makaveev D, Von Rauch M, De Wulf M, et al. Accurate field strength measurement in rotational single sheet testers[J]. Journal of Magnetism and Magnetic Materials, 2000, 215-216: 673-676.

[23] Nakano M, Nishimoto H, Fujiwara K, et al. Improve- ments of single sheet testers for measurement of 2-D magnetic properties up to high flux density[J]. IEEE Transactions on Magnetics, 1999, 35(5): 3965-3967.

[24] Mori Y, Miyagi D, Nakano M, et al. Measurement of magnetic properties of grain-oriented electrical steel sheet using 2D single sheet tester[J]. Przegl?d Elektrotechniczny, 2011, 87(9b): 47-51.

[25] Hasenzagl A, Weiser B, Pfützner H. Novel 3-phase excited single sheet tester for rotational magneti- zation[J]. Journal of Magnetism and Magnetic Materials, 1996, 160(7): 180-182.

[26] De la Barriere O, Appino C, Fiorillo F, et al. Extended frequency analysis of magnetic losses under rotating induction in soft magnetic composites[J]. Journal of Applied Physics, 2012, 111(7): 07E325(1-3).

[27] Alatawneh N, Pillay P. Test specimen shape considerations for the measurement of rotational core losses[J]. IEEE Transactions on Energy Conversion, 2012, 27(1): 151-159.

[28] Makino A, Kubota T, Yubuta K, et al. Low core losses and magnetic properties of Fe85-86Si1- 2B8P4Cu1 nanocrystalline alloys with high B for power applications[J]. Journal of Applied Physics, 2011, 109(7): 07A302.

[29] Enokizono M, Suzuki T, Sievert J, et al. Rotational power loss of silicon steel sheet[J]. IEEE Transa- ctions on Magnetics, 1990, 26(5): 2562-2564.

[30] Yang Q X, Li Y J, Zhao Z H, et al. Design of a 3-D rotational magnetic properties measurement structure for soft magnetic materials[J]. IEEE Transactions on Applied Superconductivity, 2014, 24(3): 1-4.

[31] 林楠, 王東, 魏錕, 等. 高速混合勵磁發電機的結構及調壓性能[J]. 電工技術學報, 2016, 31(7): 19-25.

Li Nan, Wang Dong, Wei Kun, et al. Structure and voltage regulation performance of high speed hybrid excitation synchronous generators[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 19-25.

[32] Wang Y H, Yan W L, Zhang G S. Adaptive simulated annealing for the optimal design of electromagnetic devices[J]. IEEE Transactions on Magnetics, 1996, 32(3): 1214-1217.

Design and Optimization of a Magnetizer for High Frequency Rotational Magnetic Characterization for Nanocrystalline Alloy

（Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China）

Rotational core loss is widely distributed in the T-joint of high frequency transformer and the stator of high speed motor. In order to have a better understanding of such properties, rotational core loss need to be characterized accurately in high frequencies. In this paper, four different magnetizing structures have been analyzed through the finite element method. The influence of the structures on the accuracy has been discussed. A new type magnetizer for high frequency two-dimensional magnetization is developed considering the physical characteristics of nanocrystalline alloy. The yoke geometric structure is optimized, which can extend the measuring frequency up to 10kHz.

Nanocrystalline alloy, 2D rotational magnetic property, high frequency magnetizer, optimization design

TM936

國家自然科學基金（51377042），河北省高等學校自然科學青年基金（QN2016200），河北省高等學校創新團隊領軍人才培育計劃(LJRC003)和新能源電力系統國家重點實驗室開放課題（LAPS16002）資助項目。

2016-03-30 改稿日期 2016-06-26

陳 龍 男，1989年生，博士研究生，研究方向為磁性材料特性。E-mail: zhouhuoxuan@sina.com

汪友華 男，1964年生，教授，博士生導師，研究方向為電磁場數值計算和全局優化設計。E-mail: wangyi@hebut.edu.cn（通信作者）